一种典型无人直升机操纵机构的建模与分析

齐 鸣，吉国明

(西北工业大学 航空学院，西安 710072)

一种典型无人直升机操纵机构的建模与分析

齐 鸣，吉国明

(西北工业大学 航空学院，西安 710072)

无人直升机操纵机构的输入/输出关系复杂，传统上的设计方法有很多局限，为优化操纵系统的设计，必须对操纵机构进行精确建模与分析.针对一种典型的带伺服小翼的无人直升机操纵系统，运用分析空间机构的方法建立其运动学模型，并将整个机构其分解为3个模块，对每个模块的功用进行完整的分析并给出机构运动学方程，最后对整个机构进行数值仿真.

空间机构；运动学；无人直升机；操纵机构

直升机的升力面同时为操纵面，直升机操纵系统的设计为直升机设计中的重要环节.传统上的操纵系统设计基于平面机构设计方法，优先考虑极限工作位置的位移约束，并满足工作空间的要求，利用比例系数的概念反复进行迭代设计.这种方法不能得到输入输出间的精确位移关系，并且由于要反复协调参数，设计过程较为缓慢.随着设计要求的提高，对操纵系统的尺寸、重量、刚度、空气阻力等提出了更高的要求，并且在安装自动驾驶仪的无人直升机上更希望对操纵系统的输入输出关系有一定的了解.这需要新的设计分析方法，对操纵系统进行深入细致的分析.

国内外一些学者在这方面已经做了一些工作：Lange[1]等对加拿大的CL327型无人直升机的操纵系统进行了运动学分析；Saffarian[2]等对另一种典型的小型单旋翼无人直升机的操纵系统进行了运动学分析并考虑了小翼挥舞对操纵响应的影响；袁夏明[3]等对一种共轴式全差动的无人直升机进行了运动学分析并进行了数值仿真.

虽然随着电子系统的发展，无伺服小翼的无人直升机出现了很多型号，但是机械系统的可靠性以及伺服小翼的成熟稳定使得有小翼的无人直升机(特别是在大型、跷跷板将榖形式的直升机中)依然占有很大市场.本文利用空间机构的分析方法，对一种典型的有小翼单旋翼带尾桨小型无人直升机操纵系统进行运动学分析.

1 操纵系统的运动学原理

操纵系统结构上的特点为有小翼结构，小翼称作“贝尔—希勒小翼”，兼有帮助操纵和增加稳定性的作用[4].为分析方便，将操纵系统机构分为3个模块，即自动倾斜器系统、希勒系统和贝尔系统.这3个系统都有着多个封闭的运动回路，可以写出独立的运动学方程.3个系统互相影响，共同完成控制、增稳的功能.

如图1所示为自动倾斜器系统的机构简图.大体上由杆pkjk、jkbk(k=1,2,3)、倾斜器不动环和旋转环构成.其中pk点(k=1,2,3)代表控制伺服器输入的旋转副的中心，jk、bk点(k=1,2,3)代表的球副的中心.倾斜器旋转环同不动环由一个旋转副连接，同时旋转环通过一个球副——移动复合副C同主轴相连，使旋转环可以相对主轴上下移动，并且可以绕C做三轴的转动.不动环作为空间构件应该有6个自由度，但是由于同旋转环以旋转副相连接，可知只能在主轴上以一个自由度上下移动，同时由球副b1所引出的圆柱同沟槽相接处，可知减少了一个旋转自由度，则不动环只有三个自由度.分别为沿主轴上下运动的移动自由度，以及绕球副C的两个转动自由度.这三个自由度分别对应操纵机构的总距输入以及两个方向的周期变距输入.

图1 自动倾斜器系统的机构简图

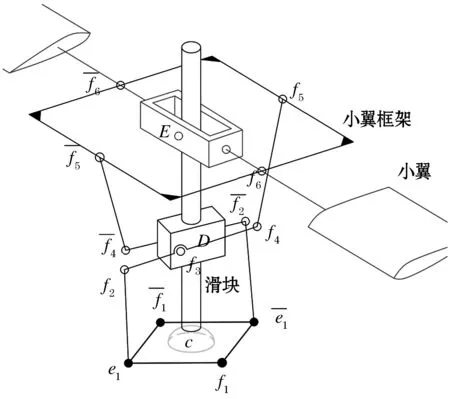
图2 希勒系统的机构简图

2 直升机操纵系统运动学建模

在对机构进行运动学分析建模的时候，考虑的主要是各部件间相对位移的关系，需要对机构进行

图3 贝尔系统的机构简图

简化，将机构中的起实际功用的部件转化为运动学意义上的构件，以各个运动副之间的关系为主要研究对象.为了实现这一目的，需要在各个构件上建立局部坐标系，局部坐标系固连在构件上，这样研究构件之间的位移关系就转变为研究各局部坐标系之间的关系，各构件的空间位移也可以用数字精确地表示出来.

2.1 自动倾斜器系统运动学建模

如图4建立机体坐标系与倾斜器不动环坐标系.首先建立机体固定坐标系x0y0z0，其次建立自动倾斜器不动环的局部坐标系x1y1z1.由上文分析得知，自动倾斜器外环有三个自由度，所以可以用三个变量来表示其空间位置.分别为C点相对O点的位移h，以及坐标系x1y1z1为达到位置先绕y1轴旋转δy°，以及其后绕x1轴旋转δx°.在旋转副p1的角度输入为θ1，p2处输入为θ2，p3处输入为θ3.下面建立此系统的位移方程.

图4 自动倾斜器系统的数学模型

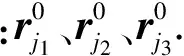
设j1b1、j2b2、j3b3杆长度分别为l21、l22、l23,根据几何同等行条件：

可以得到三个独立方程：

(1)

(2)

(3)

2.2 希勒系统运动学建模

如图5，此系统有着很强的对称性，先只取一边进行研究.在C点建立自动倾斜器旋转环的局部坐标系.xCyCzC.xC轴与x0轴之间的夹角即为主轴旋转相位角，设为ζ.f1C与xc轴的夹角为φ，即为此系统的角度输入.建立滑块的局部坐标系xDyDzD，系统参考坐标系xEyE1zE，混控臂局部坐标系xE1yE1zE1，其中yE与yE1所夹的角度为挥舞角β.Ff5与xE1轴的夹角即是小翼的迎角，设为α1.

图5 希勒系统的数学模型

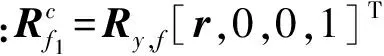
f2、f4在坐标系xDyDzD中的坐标为：

f5在坐标系xE1yE1zE1中的坐标为：

求各点在参考坐标系中的坐标.

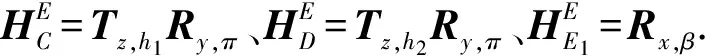
设f1f2的长度为l31，f4f5的长度为l41，根据几何同等性条件可以列出两个方程：

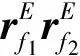
可得两个独立的方程：

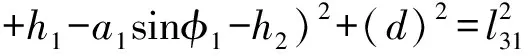
(4)

(5)

可将α1、φ1、h2看做运动参数，由上文可知系统有3个自由度，则有3个运动参数，但是现在只有两个独立方程，可知需要额外的约束.需要另一边的机构提供另外的两个方程.

在研究另一侧机构的时候，同理可以依以上方法建立局部坐标系，所得约束方程应形式应该一样.

这两个方程可化成：

(6)

(7)

φ、h1、β为输入参数，φ1、φ2、h2、α1为四个运动参数，四个独立方程，可以求解.

注意输入参数h1，设E点到坐标系x0y0z0中心O点的距离为h0为结构参数，h1=h0=h.

同时输入φ角同主轴的相位ζ相关，需要求解此关系.

2.3 倾斜器空间指向建模

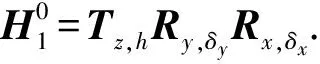
取绕y1轴逆时针旋转方向为正，据观察可知

(8)

这样，φ就成了ζ角度的函数了.

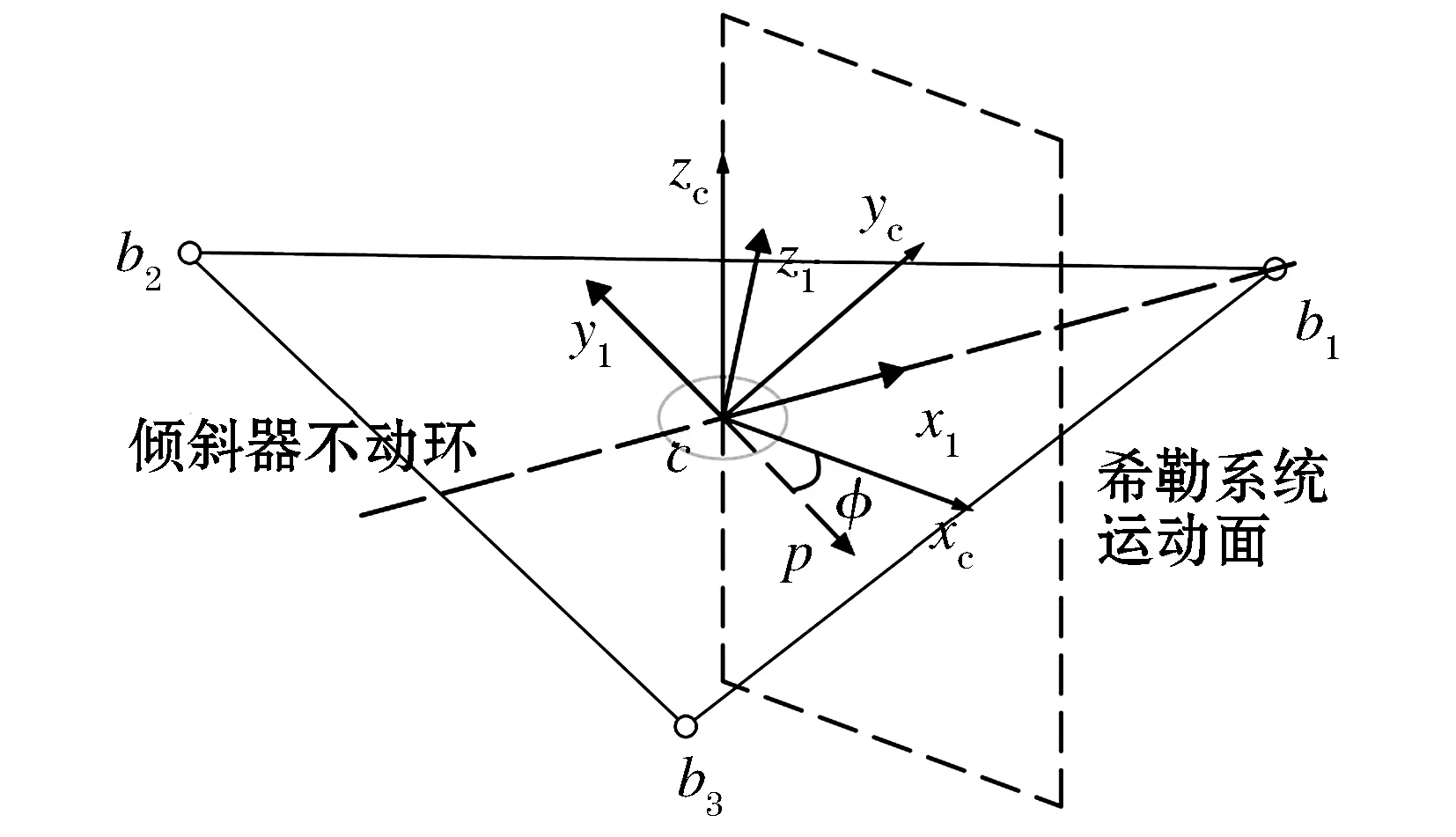
图6 希勒系统输入同倾斜器系统关系的数学模型

2.4 贝尔系统运动学建模

如图7，此系统依然有很强的对称性，可以只拿出一半进行分析求解，所不同的是可以将小翼的挥舞角看做是系统的输入角度，这样虽然系统有3个自由度，但只有两个运动参数，所以通过求解两个独立的闭合环路建立的方程就可以完全求解.

以H点为中心建立坐标系xHyHzH.

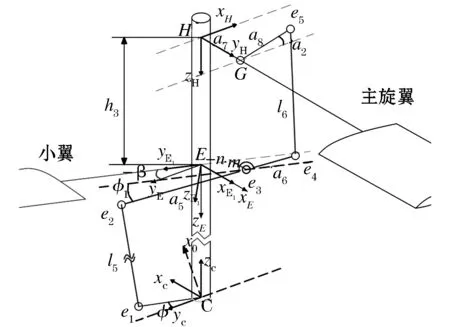
图7 贝尔系统的数学模型

Ge5与的角度设为α2，可知此角度即为桨叶的几何俯仰角.e2e4与yE1的夹角为φ1.e1C与yc的角度为φ.

求各点在局部坐标系中的坐标.

e5点在坐标系xHyHzH下的坐标为：

e2、e4点在坐标系xE1yE1zE1中的坐标为：

点e1在坐标系系xCyCzC中的坐标为：

求各点在参考坐标下的坐标：

点e1、e2、e4在坐标系xEyEzE中的坐标为：

可以列出两个方程：

(9)

(10)

φ、h1、β为输入参数，α2、φ1为带求运动参数，两个方程可以求解.

关于输入φ角可以看出同φ角有关系，事实上根据所建立的坐标系，yC轴为xC轴绕zC轴逆时针旋转ζ得到的：

(11)

3 数值仿真与分析

以上建立了整个操纵系统的闭环运动方程.模拟当小翼挥舞角为0°，自动倾斜器不动环输入总距高度为h=28 mm，输入角度δx为0°，δy分别为0°、5°、10°时，桨叶迎角α2角随主轴旋转角ζ的增长的变化.相当于自动倾斜器倾斜方向改变，做俯仰操纵时桨叶迎角相应做出改变.见图8.

图8 δy分别为0°、5°、10°时，桨叶迎角α2随主轴旋转角ζ的增长的变化

模拟当小翼挥舞角为0°，自动倾斜器不动环输入总距高度为h=28mm，输入角度δy为0°，δx分别为0°、5°、10°时，桨叶迎角α2角随主轴旋转角ζ的增长的变化.相当于自动倾斜器倾斜方向改变，做滚转操纵桨叶迎角相应做出改变.见图9.

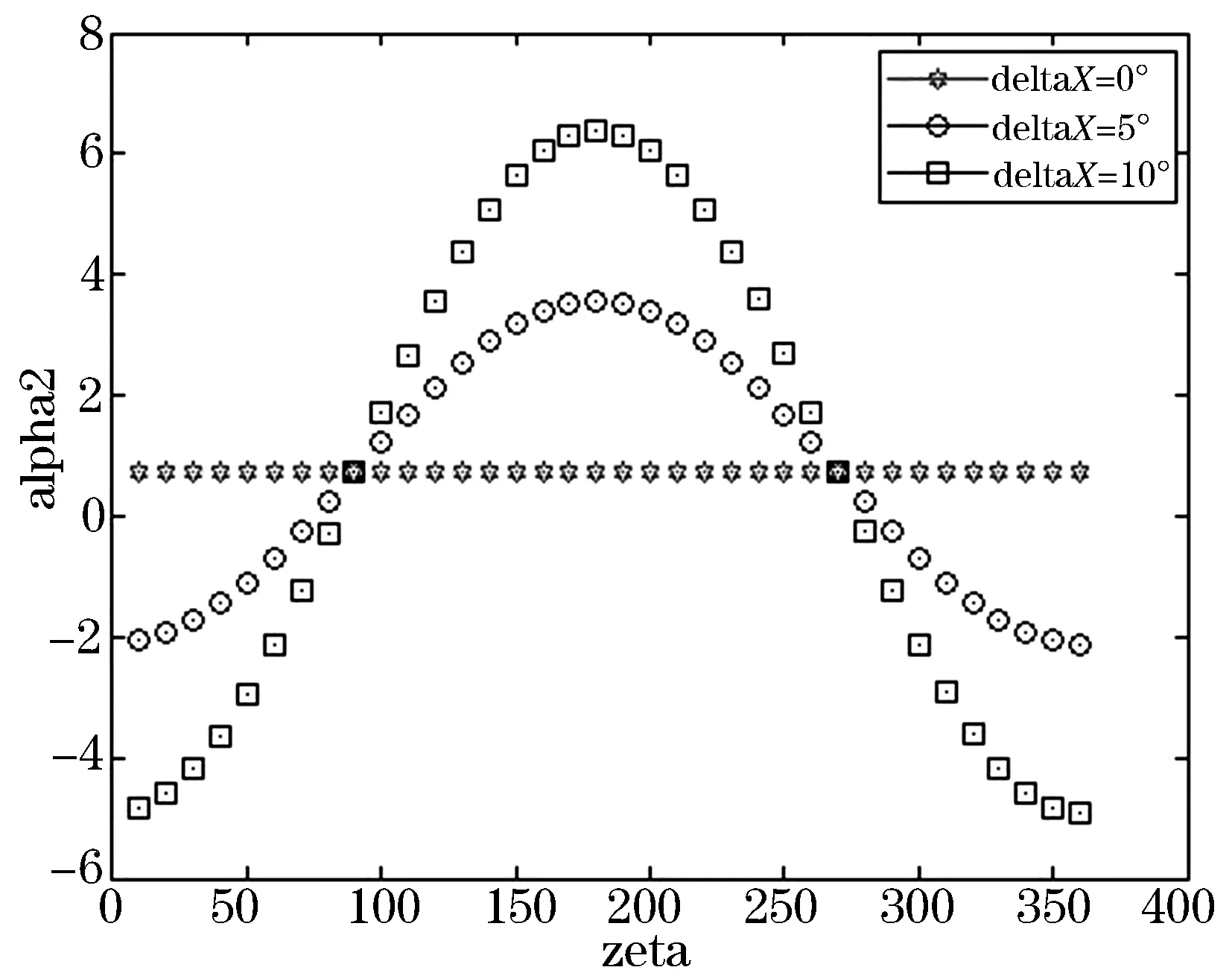
图9 δx分别为0°、5°、10°时，桨叶迎角α2随主轴旋转角ζ的增长的变化

模拟当小翼挥舞角为0°，输入角度δx为0°，δy角为10°，总距输入h分别为23、28、33 mm时，桨叶迎角α2角随主轴旋转角ζ的增长的变化.相当于自动倾斜器倾斜方向不变，做总距改变操纵时桨叶迎角相应做出改变.见图10.

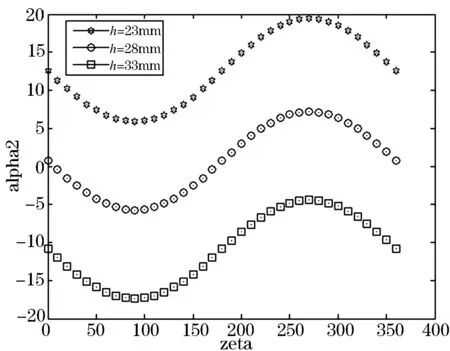
图10 总距输入h分别为23、28、33 mm时，桨叶迎角α2随主轴旋转角ζ的增长的变化

[1] LANGE C, RANJBARAN F, ANGELES J,etal. The Kinematics of the Swashplate Mechanism of a VTOL Unmanned Aerial Vehicle[J]. Multibody System Dynamics, 1999, 3: 333-365.

[2] SAFFARIAN M, FAHIMI F. A comprehensive kinematic analysis of a model helicopter's actuating mechanism [C]// 46th AIAA Aerospace Sciences Meeting and Exhibit, 2008, Reno, Nevada.

[3] 袁夏明.一种共轴式直升机操纵机构的运动学建模与分析[J].航空学报, 2013, 34(5): 988-1000.

[4] 高 正, 陈仁良. 直升机飞行动力学[M].北京: 科学出版社, 2003.

[5] 张启先. 空间机构的分析与综合(上册)[M].北京: 机械工业出版社, 1984.

Modeling and analysis of operating mechanism of a kind of typical unmanned helicopter

QI Ming, JI Guo-ming

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The input/output relationship of operating mechanism of unmanned helicopter is complex. Many limits exist in the traditional design methods. To optimize the design of the operating mechanism, it must be accurately modeled and analyzed. In this paper, the operating mechanism of a kind of typical unmanned helicopter was discussed, and the kinematics model was established by the method of spatial mechanism. The whole mechanical system was decomposed into three modules. The function of each module was totally analyzed, and the kinematics equation was established. Finally, the numerical simulation of the mechanism was given.

spatial mechanism; kinematics; unmanned helicopter; operating mechanism

2014-03-21.

齐 鸣(1988-)，男，硕士，研究方向：飞行器设计.

V275

A

1672-0946(2015)02-0242-05