双馈异步风力发电机网侧换流器复合控制策略的研究

刘新宇, 白珂

(华北水利水电大学 电力学院，河南 郑州 450045)



双馈异步风力发电机网侧换流器复合控制策略的研究

刘新宇, 白珂

(华北水利水电大学 电力学院，河南 郑州 450045)

摘要：双馈异步风力发电机(DFIG)网侧换流器的主要任务是保持直流母线电压的稳定、输入电流的正弦性和输入功率因数的恒定.一般在设计控制器时，常对电机模型进行一些理想假设，忽略掉一些次要的影响因素.在不同的运行工况下，电机参数会或多或少地发生变化，导致控制器的跟踪效果变差.为解决设计网侧换流器控制策略时由于参数变化带来的扰动不确定问题，提出了网侧换流器电流内环的基于BP神经网络整定的PI控制及电压外环的PI控制的复合控制策略.通过MATLAB/Simulink软件仿真分析，结果表明，相比于传统的PI控制，直流母线电压在电流内环的基于BP神经网络整定的PI控制及电压外环的PI控制的复合控制策略下能更快地达到给定值.因此，本文所提出的电流内环的基于BP神经网络整定的PI控制及电压外环的PI控制的复合控制策略能很好地实现对换流器输出电压和输入电流的有效控制，减小了由于参数变化等原因对换流器造成的不利影响，提高了系统的鲁棒性，具有实际意义和应用价值.

关键词：双馈异步风力发电机(DFIG);BP神经网络;网侧;复合控制

环境污染和能源紧缺是人类亟待解决的两大难题.风能、太阳能环境友好、取之不尽、用之不竭，是替代化石能源的理想选择[1].笔者围绕大型双馈风力发电系统的并网，对其网侧换流器的控制策略进行研究.

双馈风力发电机网侧换流器的任务主要包括两个方面：一方面，通过采集直流环节的直流电压进行反馈控制，从而维持直流母线电压的恒定；另一方面，通过对网侧换流器输入电流的反馈，实现网侧的单位功率因数的输入.按照对网侧换流器控制任务的要求，许多学者对其控制方法进行了大量的研究，取得了一定成果.这些成果均在某一方面展示了其有效性，但不能保证其通用性.文献[2]采用定子磁链定向的矢量控制方法，使用双闭环PI调节器对网侧换流器进行控制.文献[3-4]提出了一种基于电网电压定向的网侧PWM换流器控制策略，并将其应用在双馈发电机的并网发电上，实现了和定子磁链定向矢量控制相同的功能，克服了当电机的参数变化时，定子磁链定向的矢量控制方法的不稳定问题，且简化了算法.文献[5-6]针对基于定子磁场定向的矢量控制和基于电网电压定向的矢量控制的缺点，提出了网侧换流器直接功率控制.该控制策略是检测并网的电压与电流，计算出瞬时的有功功率与无功功率，并与给定的有功功率与无功功率进行比较，根据并网电压矢量所在的扇区，按开关表给出开关管的控制信号，通过直接对系统的有功与无功行为进行控制，使系统输出的无功功率为零.

基于DFIG网侧换流器模型和空间矢量的SVPWM控制方法，笔者提出了网侧换流器电流内环的BP神经网络自整定PI控制及电压外环的PI控制的复合控制策略，实现对DFIG并网的有效控制.

1DFIG网侧换流器数学模型的分析

网侧换流器主电路如图1所示.图中uga、ugb、ugc分别为三相电网的相电压；iga、igb、igc分别为三相输入电流；vga、vgb、vgc分别为换流器交流侧的三相电压；udc为换流器直流侧电压；C为直流母线电容；iload为直流侧的负载电流；主电路中的Lga、Lgb、Lgc分别为每相进线电抗器的电感；Rga、Rgb、Rgc分别为包括电抗器电阻在内的每相线路电阻.网侧换流器的负载则是与转子绕组相连的转子侧换流器.

图1　网侧PWM换流器的主电路图

在三相同步旋转坐标系下，网侧PWM换流器的数学模型可描述为[7]

(1)

式中：ugd、ugq分别为电网电动势的d、q分量；vgd、vgq分别为三相VSR交流侧输出电压矢量的d、q分量；igd、igq分别为三相VSR输入电流矢量的d、q分量；Sd、Sq分别为开关函数的d、q分量；ω为电网电压的角速度；L为每相进线电抗器的电感；R为包括电抗器电阻在内的每相线路的电阻.

在将同步旋转坐标系d轴定向于电网电压矢量的方向上时，ugd=ug，ugq=0 V，则式(1)可以简化为

(2)

同理，网侧换流器向电网输出的有功功率和无功功率分别为

(3)

从式(3)可以看出，电流矢量d、q轴分量igd和igq实际上代表了网侧换流器的有功电流和无功电流，而网侧换流器输出的直流母线电压是和无功功率Qg密切相关的.因此，在DFIG网侧换流器控制策略中，对网侧换流器输入电流igd、igq的有效控制对于整个控制策略至关重要.

2DFIG网侧换流器的控制策略

网侧换流器控制一般采用功率内环控制及直流电压外环控制的双闭环控制策略.

2.1　功率环控制策略的设计

由式(2)知，网侧换流器d、q轴电流除了受vgd、vgq的控制外，还受电流交叉耦合项ωLigq、ωLigd及电网电压ugd的影响.为了消除交叉耦合项的影响，引入电流状态反馈量ωLigq、ωLigd来实现解耦，并引入电网扰动电压项，从而实现了d、q轴电流的解耦控制，有效地提高了系统的动态控制性能.将式(2)转化为系统结构图，如图2所示，图中的S由拉氏变换产生.

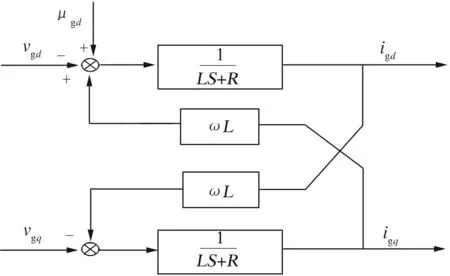
图2　d、q轴解耦系统结构图

通过对图2的分析可知， DFIG网侧换流器处于运行状态时，待控制系统的受控输出为换流器的输入电流igd、igq，控制输入为换流器输出电压vgd、vgq.为此,剔除上述扰动影响，系统方程变为

(4)

根据式(4)设计PI控制器，这里仅就d轴进行讨论，q轴可参考d轴控制器进行设计(其中带“*”上标的变量为参考值变量)，

(5)

由于参数的扰动，传统的固定参数PI控制无法快速跟踪给定值，甚至当扰动较大时，无法控制系统的稳定.文中用BP神经网络PI控制代替传统的PI控制，使系统的输出值与期望值误差最小.采用3层BP网络，并改PI控制为增量型PI控制，公式如下：

vgd=kp(e(k)-e(k-1))+kie(k).

(6)

BP神经网络的输入变量个数取决于被控系统的复杂程度，输出节点对应2个可调的PI参数.由此，构造一个3层BP网络，其结构为4-5-2.网络输入层的输入为

(7)

其中

(8)

网络隐含层的输入、输出分别为:

(9)

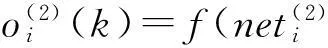
(10)

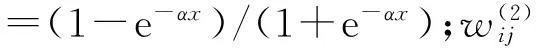
网络输出层的输入、输出分别为:

(11)

(12)

取性能指标函数为

E=0.5(r(k)-y(k))2，

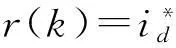
(13)

式中:η为学习速率；β为惯性系数.

(14)

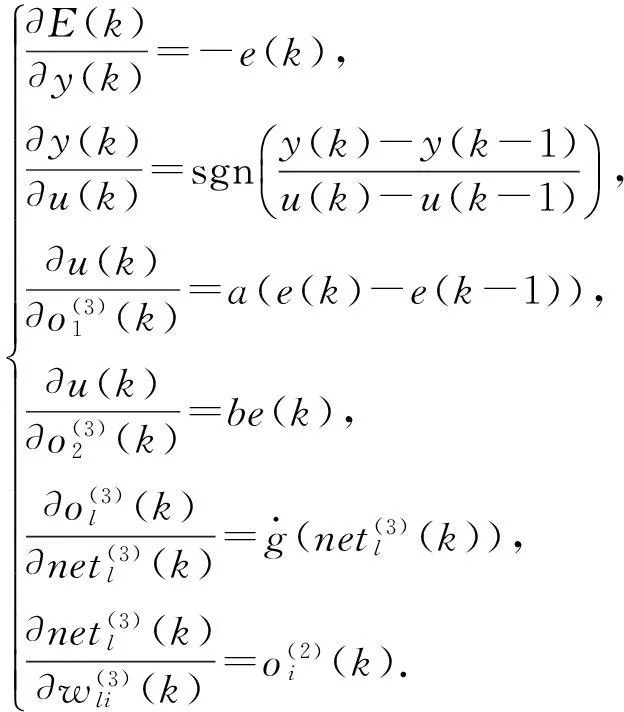
(15)

式中∂y(k)/∂u(k)由于未知，用符号函数代替，由此得网络输出层加权系数为：

(16)

同理隐含层加权系数为：

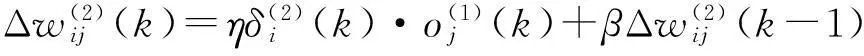
(17)

2.2　电压环控制策略的设计

直流环节电压控制器采用式(18)的方式设计[8]，即

(18)

3仿真分析

网侧换流器电压、电流双闭环控制策略如图3所示.为了对该控制策略的有效性进行验证，采用MATLAB/Simulink的Power System工具箱，建立了DFIG网侧换流器的电压-电流双闭环控制系统的仿真模型，如图4所示，其中的网侧控制器仿真模型如图5所示.

仿真中使用的参数有：电网相电压220 V，频率50 Hz，电容440 μF，直流给定电压500 V，p轴控制器参数a、b均为50，c、d均为0，学习速率η等于0.5，惯性系数β为0.04，双极S型函数系数α为0.000 1，S型函数系数α为0.002 0.同理q轴控制器参数a、b均为300，c、d均为0，学习速率η等于0.2，惯性系数β为0.02，双极S型函数系数α为0.000 2，S型函数系数α为0.000 2.

网侧控制器模型采用电压、电流双闭环结构，前者用于控制稳定的电压,后者用于控制输入的功率因数.直流母线电压给定值为500 V，并在0.5 s时突加负载，仿真结果如图6—12所示.

从图6的直流母线电压仿真结果中可以看出，2种控制方法下，电压都稳定达到500 V，虽然0.5 s时因为负载的变化导致直流电压出现波动，但电压很快又回到给定值.但当采用文中提出的BP神经网络PI控制策略时，直流母线电压的跟踪更快，超调较小.该BP神经网络整定的PI控制在0.07 s时达到稳定，而在常规PI控制方法下，电压在0.08 s时才达到稳定，超调更大一些.由此可见，文中提出的复合控制增强了直流母线电压的跟踪效率，提高了系统的稳定性.

图3　网侧换流器电压、电流双闭环控制电路图

图4　网侧换流器控制系统的仿真模型

图5　BP神经网络整定的PI网侧控制器的仿真模型

图6　直流电压仿真曲线

从图7网侧换流器输入有功功率的仿真结果中可以看出：有功功率在0.08 s左右达到稳定，约为2 500 W；当负载在0.5 s发生变化时，有功功率也相应地发生改变，并迅速达到稳定；基于BP神经网络整定的PI控制的跟踪效果要明显好于纯PI控制.

图7　输入有功功率仿真曲线

图8为网侧换流器无功功率的仿真结果，这里为了实现单位功率因数输出，给定参考信号为零，实际跟踪值在0.07 s时达到稳定且为零，并在0.5 s改变负载时仍能保持稳定.

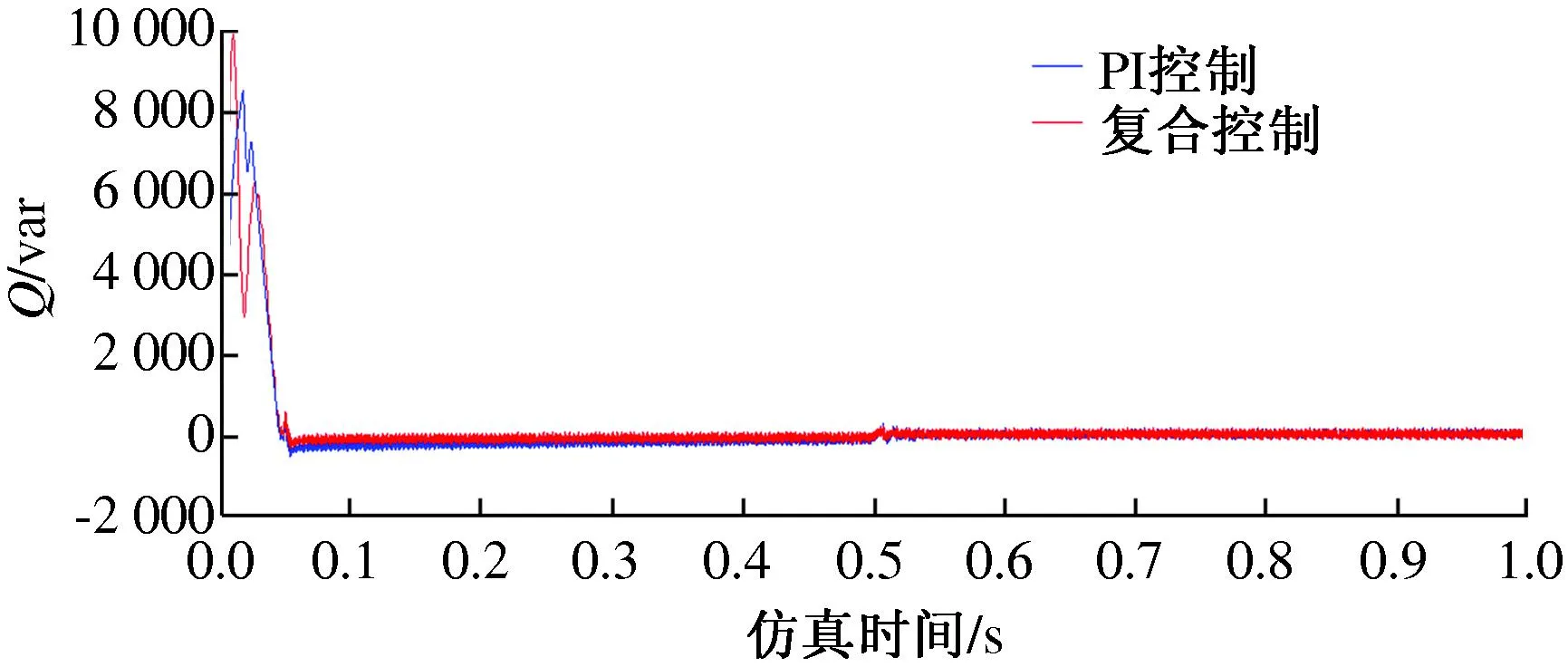
图8　输入无功功率仿真曲线

综上所述，文中所提出的BP神经网络整定PI控制相比于传统的PI控制能更加有效、快速地跟踪给定值，使系统快速进入稳态.

网侧换流器的整流状态仿真曲线如图9中所示.

图9　网侧换流器整流状态仿真曲线

可以看出：网侧电压和电流波形的相位相同，且均为正弦波，能量由电网流入换流器，实现了单位功率因数输入的设计目标.

从网侧换流器的逆变状态仿真曲线图10中可以看出，网侧电压和电流反相，电流波形近似为正弦波，能量由换流器流向电网，实现了能量的双向流动.

图10　网侧换流器逆变状态仿真曲线

图11和12分别为BP神经网络整定PI控制器的比例、积分系数变化曲线.由图11—12可知，比列系数在0.07 s左右达到稳定，其振幅在1个单位以内，并在0.5 s时仍能保持稳定，没有受到负载变动的扰动，仅仅是缓慢上升;积分系数也在0.07 s时达到稳定，同时也没有受到0.5 s时负载变动的影响，而是缓慢下滑.这说明系统静差在不断减小，而相应的积分系数也在减小；BP神经网络系统在0.07 s左右就能很好地拟合PI控制系统，权系数在0.07 s后变化较小.分析可得，系统即使在0.5 s改变了外部输入和输出环境，系统内部结构参数没有改变，因此图11和12曲线在0.5 s没有发生大的扰动，仍处在稳定状态.

图11　q轴比例系数kp变化曲线

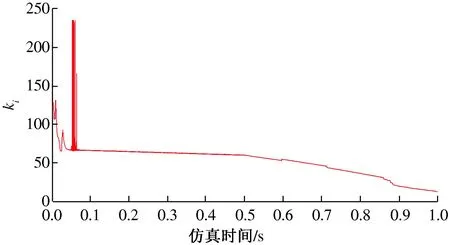
图12　q轴积分系数ki变曲线

4结语

文中针对双馈风力发电并网系统中的网侧换流器提出的电流内环的BP神经网络整定PI控制及电压外环的PI控制的复合控制策略，能够提高系统的跟踪响应，缩短了调节时间，增强了系统的稳定性.仿真结果表明，相比于传统的PI控制策略，该控制策略可以使双馈风力发电并网系统的网侧换流器控制响应时间更短，系统的稳定性更高，这对提高风力发电系统并网的质量有实际意义.

参考文献

[1]吴利乐，郑源，王爱华，等.可再生能源综合利用的研究现状与展望[J].华北水利水电大学学报(自然科学版)，2015,36(3)：82-85.

[2]Kazmierkowski M P，Dzieniakowski M A，Sulkowski W. The three phase current controlled transistor dc link PWM converter for bi-directional power flow[C].Proc PEMC Conf，1990：465-469.

[3]Barrass P，Cade M.PWM rectifier using indirect voltage sensing[J].IEE Procceedings Electric Power Applications，1999，146(5)：539-544.

[4]郎永强,许殿国,马洪飞.三相电压型PWM整流器的一种改进前馈控制策略[J].电机与控制学报,2006,10(2):160-170.

[5]谈立,阮毅,赵梅花.三相PWM变换器矢量控制与直接功率控制研究[J].电力电子技术,2013,47(12):69-71.

[6]陈伟,邹旭东,唐建.三相电压型PWM整流器直接功率控制调制机制[J].中国电机工程学报,2010,30(3):35-41.

[7]任永峰，安中全．双馈式风力发电机组柔性并网运行与控制[M].北京：机械工业出版社，2011．

[8]周天佑,郭育华.双馈风力发电系统网侧变流器的控制及仿真[J].电气开关,2010,48(2),31-34.

(责任编辑：杜明侠)

The Composite Control Strategy of Doubly-fed Induction Wind-power

Generator Grid Side Converter

LIU Xinyu， BAI Ke

(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

Abstract:The main task of doubly-fed induction wind-power generator (DFIG) grid side converter is to maintain the DC bus voltage stability, ensure inputting sinusoidal current and control input power factor. Due to the design of the controller which carry out some of the idealized assumptions, ignore some minor factors of motor, the motor parameters at different operating conditions will have more or less change, which lead to deterioration in tracking performance of controller. To solve the grid-side converter control issues strategy that parameter change brings perturbations, this paper presents a grid side hybrid control strategy which based on BP neural network tuning PI control in the inner current loop and PI control in the voltage outer-loop. Through MATLAB/Simulink software simulation, compared to conventional PI control, the DC bus voltage reached a given value more quickly under the composite control strategy based on inner BP neural network tuning PI control and voltage outer PI control. The simulation results show that the control strategy, which based on current inner BP neural network tuning PI control and voltage outer PI control, can well realize the effective control of the inverter output voltage and input current. It′s more important this method can not only reduce the adverse effects on the grid side converter due to the variations parameters and other factors, but also increases the robustness of the system. It has an important actual significance and practical application value.

Keywords:DFIG; grid side; BP neural network; hybrid control

文献标识码：A

文章编号：1002-5634(2015)06-0072-06

中图分类号：TM46

DOI:10.3969/j.issn.1002-5634.2015.06.018

作者简介：刘新宇(1976—),男,河南南阳人,副教授,硕导,博士,主要从事复杂系统建模与控制方面的研究.
白珂(1989—),男,河南郑州人,硕士研究生,主要从事大型双馈风电场并网低电压穿越联合优化控制器方面的研究.

基金项目:国家自然科学基金重点项目(41174127).

收稿日期:2015-05-30