利用不平衡推力法分析昭山地区边坡稳定性

何阳, 李帅, 林晶

(1.湖南省地质调查院，湖南 长沙410116； 2.湖南大学 土木学院，湖南 长沙 410012；

3.河南省人防建筑设计有限公司,河南 郑州 450014)



利用不平衡推力法分析昭山地区边坡稳定性

何阳1, 李帅2, 林晶3

(1.湖南省地质调查院，湖南 长沙410116； 2.湖南大学 土木学院，湖南 长沙 410012；

3.河南省人防建筑设计有限公司,河南 郑州 450014)

摘要：不平衡推力法作为一种重要的边坡稳定性分析的确定性方法，普遍应用于工程实际中.针对牵引式破坏和推移式破坏2种模式下土体条块间力的传递方式不同及相应安全系数的计算方式也存在差异的问题，引入条分法的概念，假定各条块间的相互作用力方向一致，根据这2种失稳模式下各条块间力和力矩的平衡关系，推导出相应边坡安全系数的计算公式.结合具体边坡实例，分析了这2种不同的潜在失稳模式下安全系数的差异，证实了潜在失稳模式对利用不平衡推力法评价边坡稳定性的结果影响较大.

关键词：不平衡推力法；确定性分析；边坡工程；安全系数；稳定性

在岩土工程中，极限平衡法是边坡稳定性分析中应用最广的一种方法.它假定岩土体破坏是由滑体在滑面上发生滑动造成的，将滑动面以上的块体划分为不同的小块，利用摩尔-库伦强度准则引入一些简化假定，通过每一条块体的平衡条件来建立整个边坡的平衡方程，将边坡稳定性分析的超静定问题简化为静定问题进行研究[1].

利用极限平衡法求解结构安全度时，由于其清晰的求解思路、稳定的计算精度及适中的计算量而受到国内外学者的肯定.瑞典圆弧法(Petterson， 1915)将安全系数定义为抗滑力矩与滑动力矩之比(Mr/Ms),开创了极限平衡理论的一个里程碑.而后众多学者又在此基础上提出了各种优化方法如瑞典条分法(Fellenius，1927)、Bishop模型(Bishop， 1956)、普遍条分法(N.Janbu，1954)以及非圆弧滑动面计算方法等,以上方法均利用摩尔-库伦强度准则及3个静力平衡条件来进行求解[2].

利用极限平衡法中的不平衡推力法进行边坡稳定性分析时，一个重要的前提是要确定边坡的最可能失稳模式(如牵引式、推移式等)，不同失稳模式下块体的力的传递方式不同，边坡的稳定性计算公式也有差异[3-4].而在实际工程中，某一边坡的失稳模式常常不确定，有的可能是若干种失稳破坏方式的耦合，这就增加了计算边坡稳定性的难度.同一边坡在不同失稳模式下求解得到的安全系数是不同的，因此对于边坡的稳定性评价会出现一定的误差.

鉴于此，以昭山地区一边坡为例，分别计算了天然状态及暴雨状态下该边坡在不同失稳模式下的安全系数，根据《岩土工程勘察规范》(GB 50021—2001)来评价该边坡的稳定性[5]，将所得结果与实际边坡状态进行比较分析.鉴于篇幅，文中只对2种不同失稳模式下得到的安全系数进行对比分析，而对影响边坡稳定性的具体物理力学参数及敏感性不做讨论.

1不同失稳模式下边坡的稳定性计算

不平衡推力法主要适用于潜在面为折线形的边坡稳定性计算[3].其基本思路为：先将整个滑动土体划分为n块(如图1所示)，然后，假定一个初始安全系数F，从坡顶的第1个土条开始，假设其受力P1=0，利用F、P1及有关参数求得第1个土条对第2个土条的作用力P2(即第2个土条的条间作用力)，以此力作为第2个土条所受第1个土条的影响力，以此类推，最终求得最后一个土条(坡足位置)的条间作用力.若最后一个土条的条间作用力为零或者满足要求的误差(<10-3)[6-7]，即认为安全系数F满足平衡条件.否则调整安全系数F重新计算，直至满足最后一个土条的条间作用力为零，此时的F即为该边坡的安全系数.

图1　不平衡推力法下的土条划分模型图

1.1　牵引式破坏的失稳计算

如图2所示，利用不平衡推力法进行稳定性计算时，Pi-1即为第i-1块土条的条间作用力，Pi即为第i个土条的条间作用力[4-5]，Ri为第i+1个土条抗滑力对第i个土条的作用力.

图2　不平衡推力法下的相邻条块间的受力图

将前一块的下滑力视作抗滑力，第i块滑面方向的抗滑阻力为

Pr·i=Pi-Pi-1cos(θi-1-θi)+NitanΦi-

Pi-1sin(θi-1-θi)tanΦi+ciLi，

(1)

即

Pr·i=Pi-Pi-1cos(θi-1-θi)+Qi.

(2)

其中Qi是为了表达方便引入的一个无量纲参量，

Qi=(Ni-Pi-1sin(θi-1-θi))tanΦi+ciLi.(3)

传递系数

ψi=cos(θi-1-θi)-sin(θi-1-θi)tanΦi，(4)

则相应的安全系数

Fs=Pr·i/Ti=[Pi-Pi-1cos(θi-1-θi)+NitanΦi-

Pi-1sin(θi-1-θi)tanΦi+ciLi]/Ti.

(5)

滑块底面法线方向力的平衡方程为：

Pi=Pi-1ψi-1+FsTi-Qi.

(6)

式中：Ti=Wisinθi,为重力作用下滑块底面切线方向的分量，Wi为第i块条块的重力；Ni为第 i块条块的自重在滑块底面法线方向的分量；θi为滑面水平倾角；Φi为土体内摩擦角；ci为土体黏聚力；Li为条块滑面长度.

1.2　推移式破坏的失稳计算

在推移式破坏模式下，由于土体自重作用使得条块的下滑力不断增加，而抗滑力保持不变，滑坡的荷载以此向下传递，则其第i块滑面方向抗滑力为

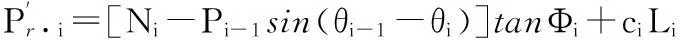
(7)

第i块滑块底面切线方向的下滑力为

Ti′=Wisinθi+Pi-1cos(θi-1-θi)-Pi；

(8)

传递系数

ψi=cos(θi-1-θi)-sin(θi-1-θi)tanΦi/Fs.

(9)

则安全系数

(10)

滑块底面法线方向力的平衡方程为

Pi=Pi-1ψi-1+FsTi-Qi.

(11)

1.3　理论分析

通过以上的计算表达式可以看出，对于同一边坡，不同的潜在失稳模式，其安全系数的计算方法不同[6-7].而在实际勘测中，仅仅根据勘察所得到的水文地质、工程地质、岩体结构特征等资料是很难确定边坡的具体失稳模式、边界范围及地质模型等.对于同一种边坡，其破坏模式常常是几种失稳模式综合作用的结果，而利用《岩土工程勘察规范》(GB 50021—2001)中的单一失稳模式进行边坡稳定性分析得到的结果是不准确的[2,8-9].文中以昭山地区一边坡为例，在天然状态和暴雨状态下，针对不同失稳模式对边坡的稳定性进行分析评价，并与实际边坡情况进行对比，以便为实际工程提供参考.

2实例分析

2.1　工程概况

湘潭市昭山工业园边坡位于湘潭市岳塘区昭山乡高峰村，中心位置地理坐标为东经113°01′51″，北纬27°57′17″，距高珠高速直线距离仅0.5 km，交通便利.在过去50 a内，该边坡一直处于稳定状态，但由于近年来修建公路时的开挖与充填使切坡形成临空面,从而大大降低了坡脚阻抗，并且边坡上游各种建筑群的建造及人类活动的频繁，增大了坡体的荷载.雨季时的降雨作用使地表水不停地入渗坡体，在基覆面附近的富水区造成坡体自重增加，坡面抗剪强度降低.目前，该坡体已经出现了明显的沉降，若不进行及时的稳定性评价及工程治理，将会使边坡变形程度增加，区域扩大，该边坡的整体稳定性将进一步降低，构成潜在地质灾害，对坡体前缘居民区造成很大的威胁.

在湖南省地质调查研究院所做的勘察及实验室所得数据的基础上，在天然状态及暴雨状态下，利用不平衡推力法计算了该边坡在不同失稳模式下的剩余下滑力及安全系数，并与边坡的实际地质状况进行了比较验证. 表1为天然及暴雨(饱和)状态下坡体的物理力学参数的平均值.

表1　坡体物理力学参数平均值

2.2　边坡稳定性的计算分析

根据该边坡的相关参数，利用上述2种算法对该边坡在天然状态及暴雨状态下的稳定性进行计算，所得有关结果见表2(F表示不同破坏模式下计算所得的安全系数).

表2　不同失稳模式下边坡的稳定性计算结果

由表2可以看出，在天然状态下，2种失稳模式下计算得到的剩余下滑力及安全系数有少许偏差，但整体差别不大，2种失稳模式下的安全系数值均大于《岩土地质勘察规范》 (GB 50021—2001)中要求的数值，即在天然状态下，该边坡处于稳定状态.

在暴雨状态下，由牵引式失稳模式计算得到的剩余下滑力明显大于推移式失稳模式下的剩余下滑力，并且安全系数也不相同.块体1在牵引式失稳模式下的安全系数为1.08，块体处于基本稳定状态，而在推移式失稳模式下得到的安全系数为1.02，块体处于欠稳定状态；块体3在推移式失稳模式下的安全系数为1.04，块体处于欠稳定状态，而在牵引式失稳模式下的安全系数为0.89时，块体处于极不稳定状态，需要及时进行防治处理，否则可能对边坡前缘造成严重的危害.

当前，昭山工业园边坡在非雨季时基本稳定，而在雨季的时候则出现了局部的沉降，中、后缘也出现了拉裂缝，前缘部分滑动较为明显，坡体处于蠕动变形阶段，其稳定性计算结果与现状变形特征较为吻合.综合2种失稳模式下的计算结果可以得出如下结论：天然状态下昭山工业园边坡处于基本稳定状态，而在暴雨状态下，坡表、坡体均产生了变形破坏，尤其前缘处于极不稳定状态，需要尽快治理，以防止雨季出现滑坡等地质灾害.

3结语

综合上述分析结果，得出以下结论：

1)在利用不平衡推力法进行边坡稳定性评价时，由于在不同的失稳模式下力的传递方式不同，从而导致计算所得到的安全系数不同，甚至相差很大，这会造成对边坡的安全性做出错误的评价.

2)2种计算模型没有优劣之分，只是适用的条件不同，这就需要在对边坡稳定性进行计算时首先对边坡的潜在失稳模式做出正确的判断，否则所得到的计算结果是不具备指导意义的.

3)对于综合2种失稳破坏模型或者2种失稳模式相互发展转化的边坡问题，实际的安全系数应综合2种破坏模型经耦合分析得到.

4)对于边坡的治理建议要建立在不同模式下的对比分析结果之上，并综合考虑多方面因素以获取准确的信息.

参考文献

[1]陈祖煜.土质边坡稳定性分析[M].北京:中国水利水电出版社,2003.

[2] 张鲁渝，郑颖人，时卫民.边坡稳定分析中关于不平衡推力法的讨论[J].岩土力学与工程学报，2005,24(1)：177-182.

[3] 时卫民,郑颖人,唐伯明，等.边坡稳定不平衡推力法的精度分析及其使用条件[J].岩土工程学报,2004,26(3):313-317.

[4] 童志怡,陈从新，徐健，等.边坡稳定性分析的条块稳定系数法[J].岩土力学,2009，30(5):1393-1398.

[5] 住房和城乡建设部.岩土工程勘察规范：GB 50021—2001[S].北京:中国建筑工业出版社,2009.

[6] 毛会永，罗志刚.厄瓜多尔某水电站左坝肩开挖边坡的稳定性评价[J].华北水利水电大学学报(自然科学版)，2015,36(2):54-57.

[7] 朱大勇,李焯芬,黄茂松，等.对3种著名边坡稳定性计算方法的改进[J].岩石力学与工程报,2005,24(2):183-194.

[8] 刘汉东，李冬冬，王忠福.基于有限元极限平衡法的生基坪滑坡稳定性分析[J].华北水利水电大学学报(自然科学版),2015,36(3):53-57.

[9]郑颖人,赵尚毅.边(滑)坡工程设计中安全系数的讨论[J].岩石力学与工程学报,2006,25(9):1937-1940.

(责任编辑:杜明侠)

Using Imbalance Thrust Force Method to Analyze the Slope Stability in Zhaoshan Area

HE Yang1, LI Shuai2, LIN Jing3

(1.Hunan Institute of Geological Survey, Changsha 410116, China；

2.College of Civil Engineering, Hunan University, Changsha 410012, China；

3.Henan Civil Air Defense Building and Design Institute Limited, Zhengzhou 450012, China)

Abstract:As an important method for stability evaluation of slope project, the imbalance thrust force method has been widely used in engineering practice. In the process of using the imbalance thrust force method to evaluate slope stability, as the transfer mode of the force in different failure modes, that is pull-type failure mode and push-type failure mode, is different, the calculation method of safety factor is different, too. In this paper, through introducing the theory of slices method and supposing that the direction of the interaction force among each sticks behave conformity, the corresponding calculation formula connected with safe factor of a slope is derived based on the equilibrium relationship between the force and the moment with respect to each sticks, under the circumstances of two different failure modes. The comparison results of safety factor between two different failure modes are shown according to a slope instances. It demonstrates the importance of the failure modes during the stability evaluation of a slope by taking advantage of the imbalance thrust force method.

Keywords:imbalance thrust force method; deterministic analysis; slope engineering; safety factor; stability

文章编号：1002-5634(2015)06-0068-04

中图分类号：P642.22;TV672.5

文献标识码：A

DOI:10.3969/j.issn.1002-5634.2015.06.017

作者简介：何阳(1988—)，男，河南漯河人，助理工程师，主要从事水文地质、工程地质与环境地质方面的研究.

收稿日期:2015-08-19
地调项目：中国地质调查“长株潭城市群地质环境调查与区划”项目(1212011220017).