城市道路路段行人过街信号设置研究
2015-03-09池利兵程国柱李德欢吴立新
池利兵,程国柱,李德欢,吴立新
(1.哈尔滨工业大学交通科学与工程学院,黑龙江哈尔滨150090;2.中国城市规划设计研究院,北京100037;3.吉林建筑大学交通科学与工程学院,吉林长春130018)
行人是出行弱势群体,尤其是在无信号的人行横道处,行人过街安全往往无法得到保障。设置行人过街信号,在时间上分离过街行人与机动车,可以有效保证行人过街安全。《人行横道信号灯控制设置规范》(GA/T 851—2009)规定:只有机动车和过街行人流率均超过规定值或者交通事故数量超过规定值时,才考虑设置行人过街信号[1]。本文认为其存在三方面不足:1)当机动车流率较高时,行人过街等待时间随之增长,当等待时间超过可容忍极限值时,行人往往会冒险穿越车流,形成严重交通冲突,甚至人车碰撞事故,在这种情况下,即使过街行人流率低于规范规定,也应设置行人过街信号;2)当机动车行驶速度较高时,过街行人与机动车的交通冲突概率随之增长,当机动车行驶速度超过严重冲突对应的阈值时,即使机动车流率低于规范规定,也应设置行人过街信号,以消除交通冲突,避免人车碰撞事故发生;3)当过街行人流率较高时,若行人连续过街将增加行车延误,此时,即使机动车流率低于规范规定,也应设置行人过街信号,以降低行车延误。
1 相关研究回顾
1.1 行人过街行为特征研究
文献[2]应用生成分析方法研究行人过街等待时间和过街尝试决策,在此基础上总结行人过街的分布规律。文献[3]调查发现女性比男性更能意识到行人过街对机动车驾驶人的干扰。文献[4]研究发现老年行人由于生理原因,对外界刺激反应较慢,穿越繁忙的机动车道和交叉口时常常手足无措,在路边等待时间较长。文献[5]研究行人过街时使用手机对安全的影响,发现过街时使用手机的行人步速缓慢,不注意周围交通状况,认知能力下降。文献[6]通过电话问卷调查,研究父母带领儿童过街时父母的安全过街行为对儿童的影响,发现只有50%的被调查父母重视对儿童的安全行为教育。文献[7]调查宗教中心的两个交叉口包含行人闯红灯、无行人过街标志/标线处穿越、机动车道旁行走、横穿道路前不观察交通状况以及携儿童过街五个方面的数据,研究宗教对行人过街行为的影响。文献[8]认为行人过街行为的决策受到距离和车速的影响,行人主要依靠与车辆间的距离而不是时间来影响其过街决定。
1.2 过街行人与机动车交通冲突研究
文献[9]分析无信号人行横道处的行人过街行为及机动车屈服特性,采用Logistic方法建立机动车屈服预测模型。文献[10]利用交通冲突理论对过街行人安全评价问题进行研究。文献[11]基于机动车车速、制动距离及行人过街速度特征,建立无信号和信号控制情况下的人-车冲突模型。文献[12]认为,过街行人一般可以接受4~6 s的穿越间隙,当车辆与行人冲突时,车辆一般会选择加速提醒行人安全避让,并建议在距人行横道50 m处对车辆进行干预,可以提高行人过街的效率和安全性。
1.3 路段行人过街设施设置条件研究
文献[13]给出过街行人信号的设置条件:交叉口或路段上过街行人日流量中的任意4 h流量不小于190人或任意1 h流量不小于50人。当行人流量满足临界条件时,交通流每小时提供的行人可接受穿越间隙数小于60人。
综上所述,国内外对行人过街行为特征及人-车冲突的研究已较为深入,而对于行人过街信号的设置研究,却没有综合考虑行人过街等待时间、行人安全度及行车延误对过街设施设置的影响,现行规范也缺少相应的定量分析与理论依据。因此,本文拟综合考虑以上因素,通过对行人过街等待时间与机动车流率、交通冲突时间与车辆行驶速度,以及行车延误与过街行人流率的关系进行研究,探求设置路段行人过街信号的机动车流率、机动车行驶速度和过街行人流率条件,为道路交通规划设计与管理部门提供相应的设计依据与决策参考,保障路段行人过街安全。
2 调查方案设计与数据分析
2.1 数据采集方法
本文以哈尔滨市为例,选取某双向6车道城市道路路段上的无信号人行横道为调查地点,分别选取工作日和非工作日进行调查,以使结果具有更广泛的适用性,选取时段为7:00—9:00。
首先,在人行横道停止线前10 m和20 m的道路上,用黄色胶带粘贴出两条明显的黄线;然后在人行道上设置三脚架及录像设备,对调查道路由东向西方向的车流及过街行人进行观测。观测的主要参数包括:行人过街等待时间、交通冲突时间、机动车行驶速度、行车延误、机动车交通量及过街行人流率。
机动车交通量及过街行人流率可由视频直接观测获得;机动车行驶速度由车辆先后通过两条黄线所用时间间接计算得出;因行人过街引起的行车延误很难由调查精确获得,本文采用车辆行驶速度的降低值表示行车延误,即机动车在没有行人通过人行横道时的行驶速度(自由流速度)与有行人通过时的速度差值,差值越大,行车延误越大;行人过街等待时间及交通冲突时间通过播放视频利用秒表测得。
2.2 数据分析
2.2.1 行人过街等待时间与机动车流率的关系
表1为调查时段内机动车流率及行人过街平均等待时间的调查结果,其中机动车流率由5 min交通量换算得到,行人过街等待时间为7:00—9:00每5 min的行人平均等待时间,工作日与非工作日均为24组数据。工作日的样本总量为546人,非工作日的样本总量为522人。
由表1可知,行人过街平均等待时间基本与机动车流率呈正相关。调查发现,部分老年人过街等待时间超过60 s,有时甚至达到90 s,其他年龄段的行人过街等待时间则基本都在60 s以下。工作日行人过街平均等待时间为20.3 s,机动车流率约为2 500~3 400辆·h-1;非工作日行人过街平均等待时间为12.2s,机动车流率约为1600~2900辆·h-1。这表明,工作日机动车流率较大,行人过街等待时间较长;非工作日情况相反。
2.2.2 交通冲突时间与车辆行驶速度的关系
交通冲突一般用时间或距离进行度量。本文采用时间表征过街行人与机动车的交通冲突程度,定义交通冲突时间为:过街行人与机动车先后到达冲突地点的时间差值。其计算(观测)方法为:机动车从无冲突点到达冲突点的时间减去行人从无冲突点到达冲突点的时间。其中,交通冲突点指行人与机动车运行轨迹的交点。
在调查时段内随机选取60组行人与机动车冲突,统计数据如表2所示。数据显示,交通冲突时间为1.2~3.8 s,在这一范围内,随着机动车行驶速度增加,行人与机动车的冲突时间减小,即交通冲突严重程度增加。调查时段内,人行横道未出现人车相撞的交通事故,可以认为当人-车冲突时间大于1.2 s时,不会发生交通事故;当冲突时间大于3.8 s时,行人过街存在较大穿越间隙,行人或驾驶人有相对充裕的时间避让,行人与车辆的冲突较轻。
2.2.3 行车延误与过街行人流率的关系
本文采用机动车行驶速度降低值表征行车延误,表3为调查时段内过街行人流率及行驶速度降低值的统计数据。其中,过街行人流率由7:00—9:00每5 min内过街行人流量换算得到;行驶速度降低值为5 min内无行人通过时机动车平均速度与有行人通过时机动车平均速度的差值,工作日与非工作日均为24组数据。本次调查行人样本量为1 068人,机动车样本量为1 820辆。
由表3可以看出,随着过街行人流率的增长,车辆行驶速度降低值越来越大,即行车延误增大。经统计分析得到工作日平均过街行人流率为273人·h-1,平均行驶速度降低值为26.3 km·h-1;非工作日平均过街行人流率为261人·h-1,平均行驶速度降低值为24.4km·h-1。可以看出,调查路段工作日过街行人流率大于非工作日,相应的速度降低值也较大。
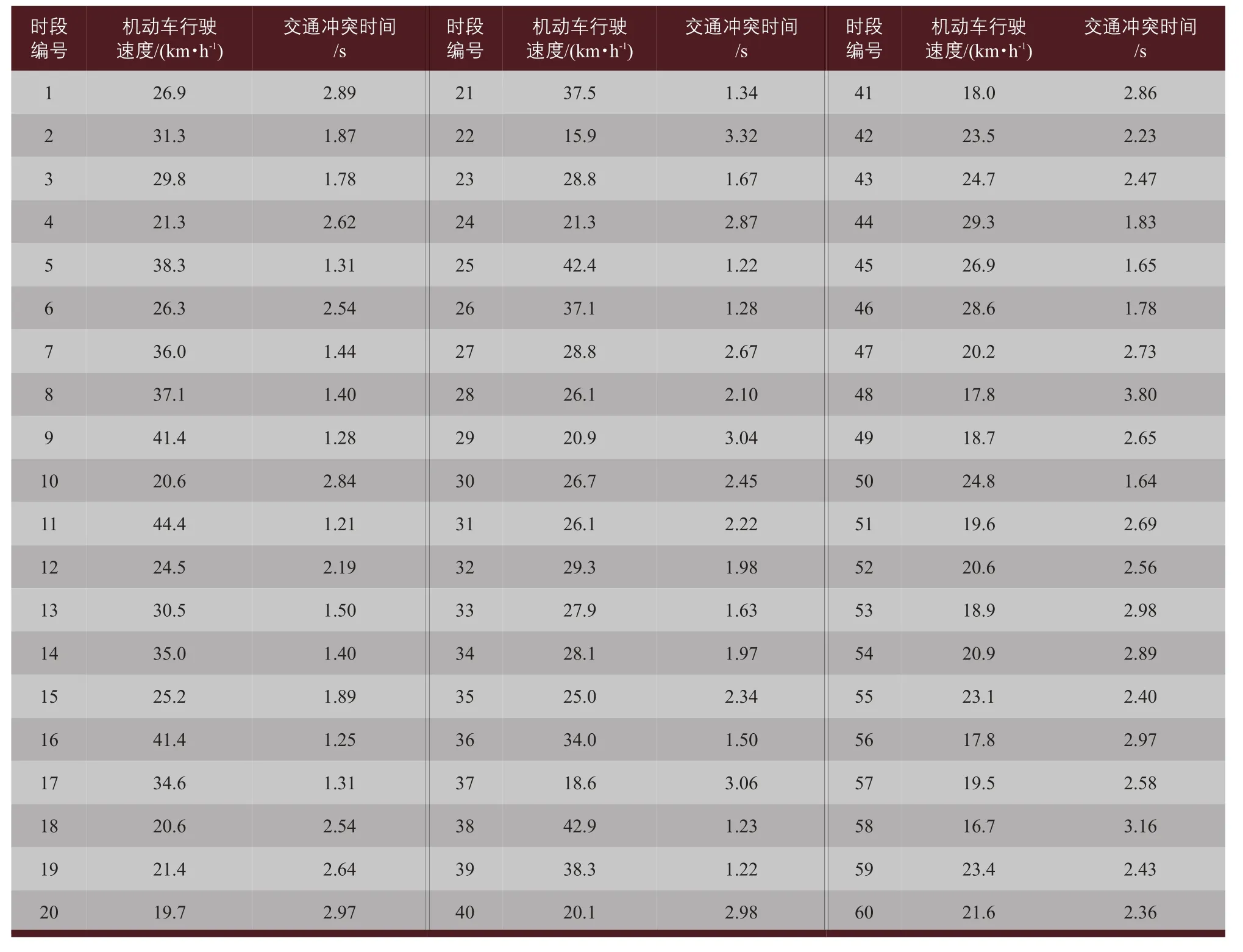
表2 交通冲突时间与行驶速度统计Tab.2 Statistics on traffic conflict time and driving speed
3 模型构建
3.1 行人过街等待时间与机动车流率模型
如图1所示,行人过街等待时间随着机动车流率的增长而增长。选取指数函数、二次函数和三次函数进行曲线拟合(见表4),三次函数的拟合度最高,其次是二次函数和指数函数。其中,Tw为行人过街等待时间/s;Q为机动车流率/(辆·h-1)。
从定性分析来看,随着机动车流率增长,行人过街等待时间应该增大,所以在自变量(机动车流率)大于0的前提下,模型关系应该是一个单调递增函数,而二次函数和三次函数在机动车流率大于0的情况下并非单调递增。因此,在机动车流率较小时,选取指数函数更为合适。此外,因为三次函数和二次函数的拟合度相差很小,为了计算方便,在机动车流率较大时运用二次函数模型。表4中二次函数的对称轴为Q=1 974,则行人过街等待时间与单向机动车流率的关系模型为

3.2 交通冲突时间与行驶速度模型
如图2所示,交通冲突时间随着机动车行驶速度提高显著减小,即冲突更为严重。选取幂函数、二次函数和指数函数进行曲线拟合(见表5),幂函数和指数函数的拟合度均较高。其中,Tc为机动车与过街行人的交通冲突时间/s;V为机动车行驶速度/(km·h-1)。
但是,当自变量趋近于0时,指数函数趋近于一个正值;而当机动车车速趋近于0时,交通冲突时间无限大,这时可以当作交通冲突不存在,所以交通冲突与机动车行驶速度的关系模型选取幂函数更为合适,模型表达式为
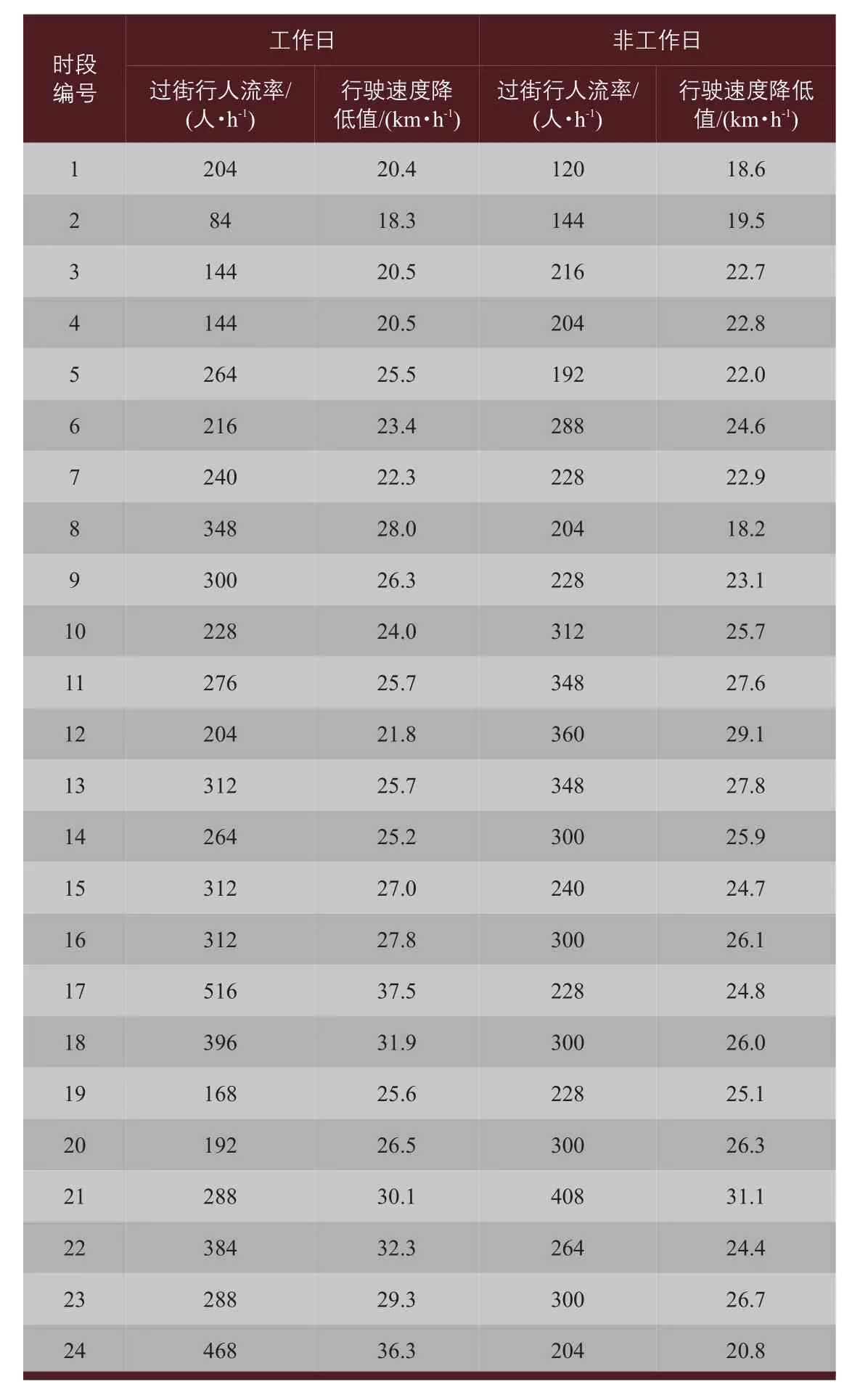
表3 行车延误与过街行人流率统计Tab.3 Statistics on vehicular delay and pedestrian flow

表4 行人过街等待时间与机动车流率回归关系模型Tab.4 Regression model of pedestrian waiting time and vehicular flow
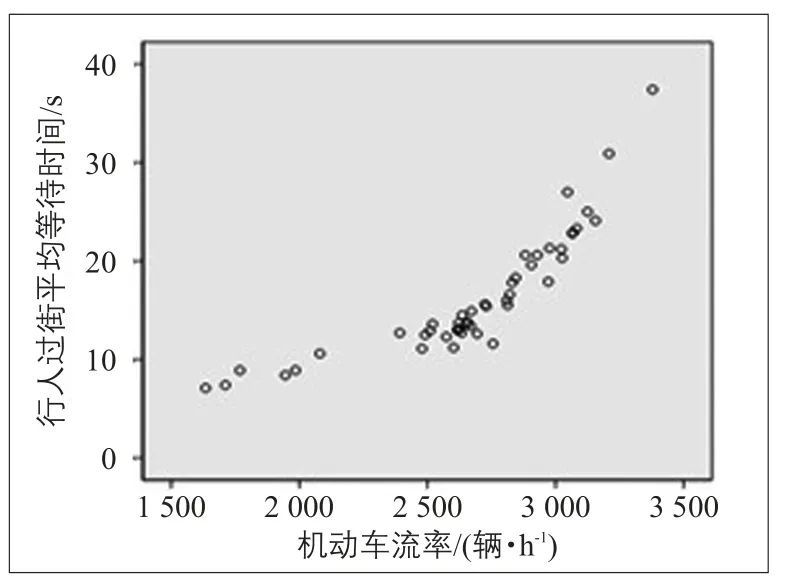
图1 行人过街平均等待时间与机动车流率散点图Fig.1 Scattered plots of pedestrian waiting time and vehicular flow

3.3 行车延误与过街行人流率模型
机动车流率越大,行人过街的机会数越少;反之,过街行人越多,机动车行车延误越大。所以,当过街行人流率达到一定值后,为了保证机动车行车延误不致于影响道路服务水平,路段人行横道应该考虑采用信号控制。
如图3所示,随着过街行人流率的增长,行驶车速降低值显著增加。选取线性函数、二次函数和指数函数进行曲线拟合(见表6),线性函数的拟合度最高。其中,ΔV为行驶车速降低值(行车延误)/(km·h-1);QP为过街行人流率/(人·h-1)。模型表达式为

4 行人过街信号设置条件
4.1 机动车流率
对行人过街平均等待时间数据进行统计分析(见图4),可以看出行人可容忍的时间最长为70~80 s,然而在等待时间为45 s时,已经有80%的人强行穿越。本文在计算行人过街信号设置的机动车流率阈值时,采用过街行人能够忍受的等待时间为45 s。
根据式(1)可得1 200辆·h-1时,建议在人行横道处设置行人过街信号。
4.2 机动车行驶速度
在本次交通调查中,交通冲突时间为1.2~3.8 s,且没有出现交通事故,因此可以认为交通冲突时间小于等于1.2 s时,容易发生交通事故。本文取1.3 s作为严重冲突时间的阈值。
根据式(2)可得


图2 交通冲突时间与行驶速度散点图Fig.2 Scattered plots of traffic conflict time and driving speed
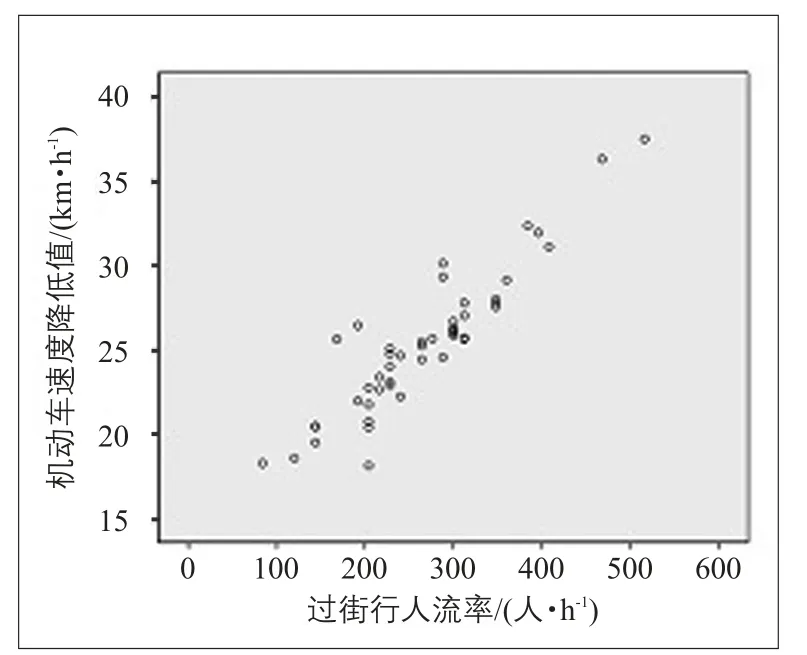
图3 行车延误与过街行人流率散点图Fig.3 Scattered plots of vehicular delay and pedestrian flow

表5 交通冲突时间与行驶速度关系模型Tab.5 Relationship between traffic conflict time and driving speed

表6 行车延误与过街行人流率关系模型Tab.6 Relationship between vehicular delay and pedestrian flow
将TW=45 s带入式(4),得到Q=3 606辆·h-1,而该调查路段单向车道数为3条,即平均每车道高峰小时交通量为1 202辆·h-1。因此,城市干路路段高峰小时交通量大于

将交通冲突时间下限1.3 s带入式(5),得到机动车行驶速度为56 km·h-1。即当行驶速度接近或大于56 km·h-1时,交通冲突比较严重,存在巨大安全隐患。取整后本文建议在机动车行驶速度超过55 km·h-1时,路段人行横道设置行人过街信号,以确保行人过街安全。

图4 行人过街平均等待时间分布Fig.4 Distribution of pedestrian waiting time on road segments

表7 设置行人过街信号的过街行人流率阈值Tab.7 Thresholds of pedestrian crossing flow for setting of mid-block pedestrian crossing signals
4.3 过街行人流率
中国一般采用行车延误作为交叉口服务水平的评价指标,而对于路段的服务水平缺少相应评价指标。美国《道路通行能力手册》(HighwayCapacityManual2010,HCM2010)中采用行程速度作为城市道路服务水平的评价指标[15]。从自由流速度来看,中国城市主、次干路分别对应于美国城市道路的III,IV级,服务水平一般选取C,D。
本文在构建行车延误与过街行人流率关系模型中,以速度降低值作为行车延误的评价指标,这里的速度降低值指自由流速度与受到行人过街影响后的行驶速度差值。城市道路路段的自由流速度分别为:主干路55 km·h-1、次干路45 km·h-1[15];将自由流速度与C,D服务水平对应的平均行程速度之差作为速度降低值(见表7)。
根据公式(3)可得

将表7中的速度降低值ΔV代入公式(6),可计算得到城市主、次干路在C,D级服务水平条件下设置行人过街信号的过街行人流率阈值(见表7)。
5 结语
本文构建了行人过街平均等待时间与机动车流率模型,对模型进行定性分析得出:机动车流率与行人过街平均等待时间呈正指数(机动车流率<1 974辆·h-1)及正二次抛物线关系(机动车流率≥1 974辆·h-1);当单车道机动车流率大于1 200辆·h-1时,建议设置路段行人过街信号。
同时,构建了交通冲突时间与行驶速度模型,分析发现人-车冲突时间与机动车车速呈负幂函数关系。当行驶速度大于55 km·h-1时,建议设置路段行人过街信号。
此外,行车延误与过街行人流率呈正线性关系,并确定了城市主、次干路路段在C,D级服务水平下设置行人过街信号的行人流率阈值,分别为305人·h-1,192人·h-1和442人·h-1,305人·h-1。
本文研究基于双向6车道路段,在下一步研究中,可对双向2,4,8车道分别进行分析研究。另外,可在已构建的两个参数间的关系模型基础上,开展多参数间的多元非线性关系模型研究。
[1]GA/T 851—2009人行横道信号灯控制设置规范[S].
[2]Hamed M.Analysis of Pedestrians'Behavior at Pedestrian Crossings[J].Safety Science,2001,38(1):63-82.
[3]Yagil D.Beliefs,Motives and Situational Factors Related to Pedestrians'Self-reported Behavior at Signal-controlled Crossings[J].Transportation Research Part F,2000,3(1):1-13.
[4]Zeeger C V,Stutts J C,Huang H,Zhou M,Rodgman E.Analysis of Elderly Pedestrian Accidents and Recommended Countermeasures[J].Journal of Safety Research,1996,27(2):128.
[5]Hatfield J,Murphy S.The Effects of Mobile Phone Use on Pedestrian Crossing Behavior at Signalized and Unsignalized Intersections[J].Accident Analysis and Prevention,2007,39(1):197-205.
[6]Lam L T.Factors Associated with Parental Safe Road Behaviors as a Pedestrian with Young Children in Metropolitan New South Wales,Australia[J].Accident Analysis&Prevention,2001,33(2):203-210.
[7]Rosenbloom T,Nemrodov D,Barkan H.For Heaven's Sake Follow the Rules:Pedestrians'Behavior in an Ultra-orthodox and a Nonorthodox City[J].Transportation Research Part F,2004,7(6):395-404.
[8]Schmidt S,Frber B.Pedestrians at the Kerb:Recognizing the Action Intentions of Humans[J].Transportation Research Part F,2009,12(4):300-310.
[9]Bastian J S,Nagui M R.Event-based Modeling of Driver Yielding Behavior at Unsignalized Crosswalks[J]. Journal of Transportation Engineering,2011,137(7):237-240.
[10]Pietrantonio H,Tourinho L F B.A Decisionbased Criterion for Selecting Parameters in the Evaluation of Pedestrian Safety Traffic Conflict Analysis Technique[J].Transport Planning and Technology,2006,29(3):183-216.
[11]Tarek S,Sany Z.Traffic Conflict Standards for Intersections[J].Transport Planning and Technology,2009,22(4):309-323.
[12]张海萍.无信号人行横道处行人过街选择行为研究[J].科技创新导报,2011(22):109-110.
[13]Federal Highway Administration.Manual on Uniform Traffic Control Devices[R].Washington DC:Department ofTransportation,2000.
