广州某院门诊量的ARIMA模型预测*

中山大学孙逸仙纪念医院（510120） 薛允莲

广州某院门诊量的ARIMA模型预测*

中山大学孙逸仙纪念医院（510120） 薛允莲

目的对门诊量序列进行预测，分析预测效果。方法采用时间序列ARIMA模型，对原始门诊量序列和调整1～2月门诊量后的序列进行预测，并在调整预测值基础上计算2月份的校正预测值。结果调整后序列的相对预测误差绝对值均值为3.84，明显小于原始序列的相对预测误差绝对值均值7.10。结论调整1～2月门诊量序列的预测效果明显优于原始门诊量序列的预测效果。

门诊量 ARIMA模型 移动假日效应 预测

随着信息化的进展，统计预测越来越成为现代医院管理工作不可或缺的工具［1］。门诊量是衡量医院门诊业务量发展的重要指标之一。通过对既往门诊量数据动态变化的分析，能够科学、准确的进行预测，合理安排人财物等资源，提高经济和社会效益。由于每年的春节在1月或2月出现，移动春节效应会影响门诊量序列的预测效果。本研究用ARIMA模型比较原始门诊量序列的预测效果和调整1－2月门诊量，并校正2月门诊量后预测效果的差异。

对象与方法

1.研究对象

本次研究利用2005年1月至2012年12月广州市某三甲医院每月门诊量数据进行建模，利用2013年的每月门诊量数据进行模型拟合效果的评价。

2.方法

（1）对原始门诊量序列的ARIMA预测

本文称原始门诊量序列的预测值为原始预测值。ARIMA预测的步骤主要是模型识别、模型选择和建模［2］。

（2）对调整门诊量序列的ARIMA预测

用调整1～2月份的门诊量序列预测后，校正2月份的门诊量预测值，得出最终的校正预测值。将2月份的校正预测值替代2月份的调整预测值，与其他月份的调整预测值一起考察调整后序列的预测效果。

①对调整1～2月门诊量序列后的预测

为了降低移动春节效应的影响，本研究对1～2月门诊量序列进行调整：1月份调整门诊量＝mean（2～12月门诊量），2月份调整门诊量＝mean（1月、3月～12月门诊量）。对调整后的门诊量序列进行预测，将所得预测值称为调整预测值。

②移动假日效应（春节）影响月份的预测值校正

在调整预测值的基础上，对春节影响月份的门诊量预测值进行校正：根据工作经验，春节对门诊量影响的时间段主要是春节及节后至农历正月十五。由于2013年春节日期为2月10日，故春节移动假日效应对门诊量的影响主要在2月份，本次研究中对门诊量的校正也是针对2月份的数据。

校正主要通过线性回归完成，为两步：（1）因变量：2月份门诊量比例＝2月份原始门诊量／（1月＋2月）原始门诊量和；自变量：落入2月份的天数，以1.31日为0点，向前记为负数，向后记为正数。通过线性回归得出2013年的2月份门诊量比例。（2）因变量：差值和＝（1月＋2月）原始门诊量-（1月＋2月）调整门诊量；自变量：年份。通过线性回归得出2013年差值和。

根据2月份门诊量比例和2013年差值和，得出2月份门诊量校正值。2月份校正预测值＝2月份调整预测值＋2月份门诊量校正值。

（3）预测效果评价指标

用相对预测误差绝对值进行原始预测和调整预测的预测效果比较。相对预测误差绝对值abs＝abs（（实际值-预测值）／实际值）×100%。

结 果

1.原始门诊量序列的预测

2005年1月至2012年12月的门诊量序列图见图1。可见，序列总体呈上升趋势，每年春节后有明显的下降，初步判断存在年度周期。对序列进行年度差分，对差分后序列进行ARIMA建模。

图1 2005年1月至2012年12月的门诊量序列的时序图

根据ARIMA建模方法，选择疏系数模型：自回归部分为1＋0.36074 B（1）；移动平均部分为1-0.85004 B（12）。预测效果见表1。

2.调整门诊量序列的最终预测

对1～2月门诊量调整后的序列进行预测。根据ARIMA建模方法，选择疏系数模型：自回归部分为1＋0.22718 B（4），移动平均部分为1-0.50782 B（12）。调整序列的预测效果见表1。

以2月份观测值比例（Y1）为因变量，以落入2月份的天数（X1）为自变量建立线性回归方程，Y1＝55.602＋2.322X1；R2＝0.723，P＝0.007＜0.05。根据2013年X1＝10，可知2013年2月份观测值比例为78.822。见表1。

以差值和（Y2）为因变量，以年份（X2）为自变量建立线性回归方程（因2007年观测值为异常值，故剔除），Y2＝3332482.152－1688.862X2；R2＝0.663，P＝0.026＜0.05。根据2013年X2＝2013，可知2013年差值和为－67197.05。根据Y2和Y1可知，2013年2月份的校正预测值＝2月份的调整预测值＋Y2×Y1× 0.01＝106040.0。见表2。

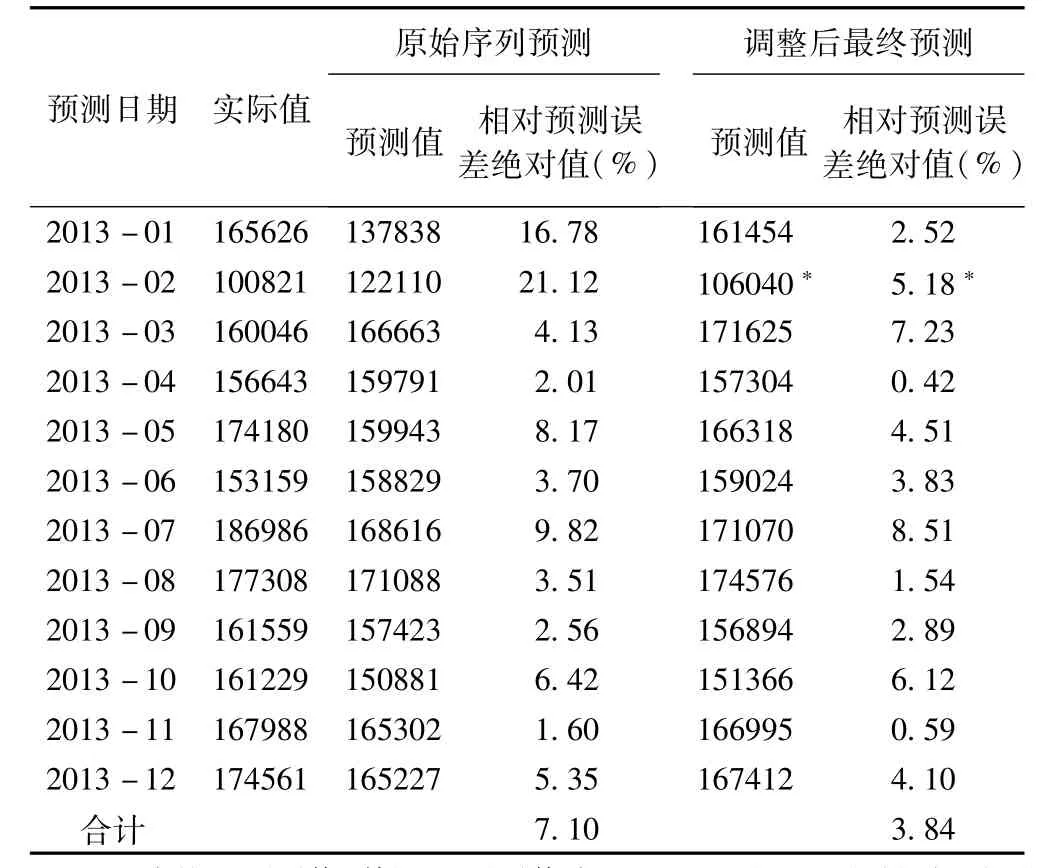
表1 原始序列和调整序列的ARIMA模型预测结果

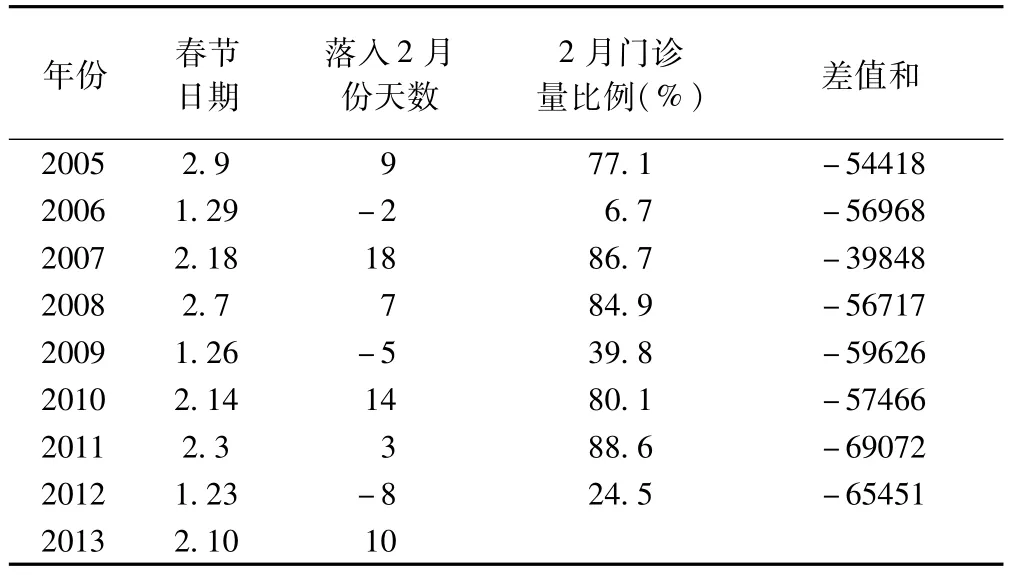
表2 回归分析用数据

讨 论

ARIMA模型又称求和自回归移动平均模型，这一模型是建立在历史数据基础上的，因此对历史数据的搜集时间有一定要求（一般要求多于50个点），通常，历史数据越多，模型的准确性越高。

在用ARIMA模型进行预测时，需要注意移动假日效应的影响。移动假日效应是指假日在各年出现的公历日期不同，具体表现为以下两个特征［3］：①假日前后序列测量的活动规律有上升或下降趋势，②假日对某相邻两个月（公历）的影响程度依赖于每年出现的不同日期。节假日在公历日期上的“移动”最直接表现为各年某些月份（如春节影响的1、2月份）观测指标的不可比，甚至影响季节调整的效果［4］。Edward等［5］指出调整移动假日效应能提高序列的预测效果。

本文分别对原始门诊量序列和调整1～2月门诊量后的序列进行ARIMA建模和预测，并对2月份的调整预测值进行移动假日效应的校正，用2月份的校正预测值替代2月份的调整预测值。从预测效果看，调整预测的预测误差绝对值均值明显小于原始序列的预测误差绝对值均值。可见，移动春节效应降低了序列的预测效果，这可能与移动春节效应对序列的时域和频域均产生影响有关［6－7］。可见，在序列进行预测研究之前，有必要对移动假日效应进行调整。

致谢：非常感谢中山大学公共卫生学院张晋昕副教授对本论文的指导和帮助。

1.周忠彬，吕红梅，邹郢.ARIMA干预模型在医院门诊量预测中的应用.中国医院统计，2008，15（2）：110-112.

2.肖枝洪，郭明月.时间序列分析与SAS应用，2009：13-109，145-163.

3.X-12-ARIMA Reference Manual.Version 0.3.Time Series Staff Statistical Research Division Room.U.S.Census Bureau，Washington，2007.http：／／www.census.gov／srd／www／x12a／

4.Alper CE，Aruoba SB.Moving Holidays and Seasonal Adjustment：The Case of Turkey.Review of Middle East Economics and Finance，2004，2（3）：203-209.

5.Edward E.Leamer.Workday，holiday and calendar adjustment with 21st century data：monthly aggregates from daily diesel fuel purchases.2011，C81：http：／／www.nber.org／papers／w16897

6.薛允莲，张晋昕.时间序列分析中的移动假日效应.中国卫生统计，2009，26（5）：502-504.

7.薛允莲，张晋昕，刘贵浩，等.医院住院人数序列的春节效应调整.中国卫生统计，2010，27（5）：473-476.

（责任编辑：郭海强）

*广东省医学科研基金（No.B2014126）