常见定量资料应用基于秩转换类参数方法的可行性*

南方医科大学公共卫生与热带医学学院生物统计学系（510515） 叶韵韶 陈平雁

常见定量资料应用基于秩转换类参数方法的可行性*

南方医科大学公共卫生与热带医学学院生物统计学系（510515） 叶韵韶 陈平雁△

目的针对配对样本（单样本）设计、两个和多个独立样本设计的定量资料，分析参数方法、非参数方法以及基于秩转换类参数方法在资料不满足参数方法条件下的适用情形。方法介绍基于秩转换类参数方法的原理及其与非参数方法的关系，采用Monte-Carlo模拟方法，考虑正态和左偏态两种分布，方差齐与不齐两种情形，比较三种方法的I类错误率和检验效能。结果左偏态分布时，无论方差是否齐性，或不涉及方差齐性（单样本设计），参数方法的I类错误率偏离设定水准且明显大于非参数方法和基于秩转换类参数方法，而检验效能明显低于其他两种方法。方差不齐且正态分布时，参数方法的统计性能明显优于其他两种方法。非参数方法和基于秩转换类参数方法在不同资料类型下的统计性能相近。结论基于秩转换类参数方法与非参数方法条件性能相近，适用于非参数方法处理的数据。

定量资料 参数方法 非参数方法 秩转换 I类错误率 检验效能

对于定量数据，参数方法通常需要满足某些前提条件，如正态分布和方差齐性等，此种情况下使用参数方法优于非参数方法已有定论。然而，当数据不满足参数方法所需条件时，包括经数据转换后仍然不能满足的情形，校正的参数方法（如Welch法等用于方差不齐的情况）和非参数方法都可以考虑［1］，同时，基于秩转换类参数方法（method of ranks，以下简称“秩转换类参数方法”）也是一种选择［2－5］。虽然Conver等［6］通过理论推导及证明，揭示了常见资料类型秩转换类参数方法统计量与非参数方法统计量之间的关系，但是，采用秩转换类参数方法在应用方面是否可行，仍是一个值得探讨的问题。为此，本文针对常见的资料类型，即配对样本（单样本）设计、两个和多个独立样本设计的定量资料，系统介绍相应的秩转换类参数方法，并采用Monte－Carlo方法模拟比较其与参数方法、非参数方法的统计性能，以系统论证秩转换类参数方法应用于数据处理实践的可行性。

方法原理

1.配对样本设计

非参数方法：对于配对样本设计，用Di表示配对样本（Xi，Yi）的差值，即Di＝Xi－Yi（i＝1，2，…，N），N为样本量。设Ri为Di对应的秩次（差值为0不进行排秩），即Ri＝sign（Di）×rank（｜Di｜），其中sign（）表示符号函数，rank（）表示｜Di｜在｜D1｜，｜D2｜，…，｜Dn｜（n是差值非0的对子数）中的秩次，当｜Di｜相等时，即出现相同秩（ties），此时取平均秩次，由此得非参数方法Wilcoxon signed ranks（WSR）的检验统计量［7］：

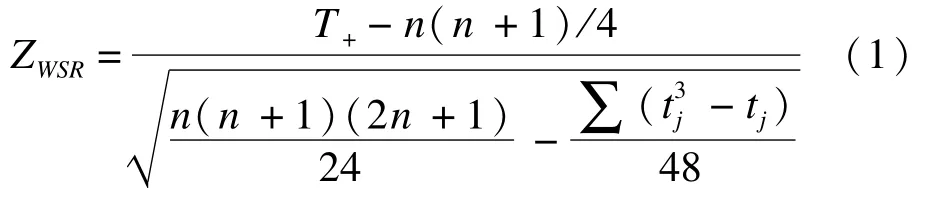
ZWSR近似服从标准正态分布，其中T＋为所有正值的秩和。tj为第j个相同秩的个数。

当无相同秩时，公式（1）等价于：

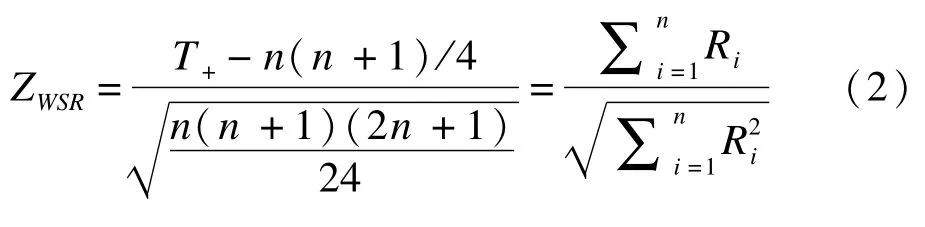
参数方法：H0∶E（D）＝0，参数方法对应的单样本t检验为：

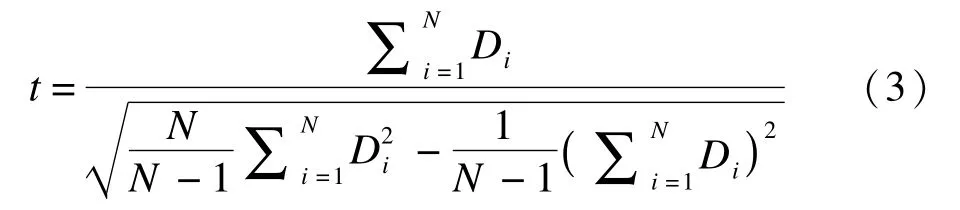
秩转换类参数方法：用秩次Ri替代原始数据Di，差值为0时做剔除处理，则秩转换类参数方法的检验统计量（单样本t检验）：

tWSR服从自由度υ＝N－1的t分布。

当不存在相同秩时，可由公式（2）和公式（4）得出检验统计量ZWSR与tWSR的关系，即：

对于单组设计，检验统计量只需在分子上减去已知参数（常量），其他关系式不变。

2.两独立样本设计

非参数方法：非参数方法常用Wilcoxon－Mann－Whitney（WMW）检验。设X1，X2，…，Xn和Y1，Y2，…，Ym表示两个独立随机样本，其中n≤m，n和m为相应两组的样本量。设Ri为两个独立样本数据混合后对应的秩次，Ri的取值从1到N（N＝n＋m）。当观测值相等时，取平均秩次，可得检验统计量：秩转换类参数方法：秩转换类参数方法（两独立样本t检验）的检验统计量［6］：

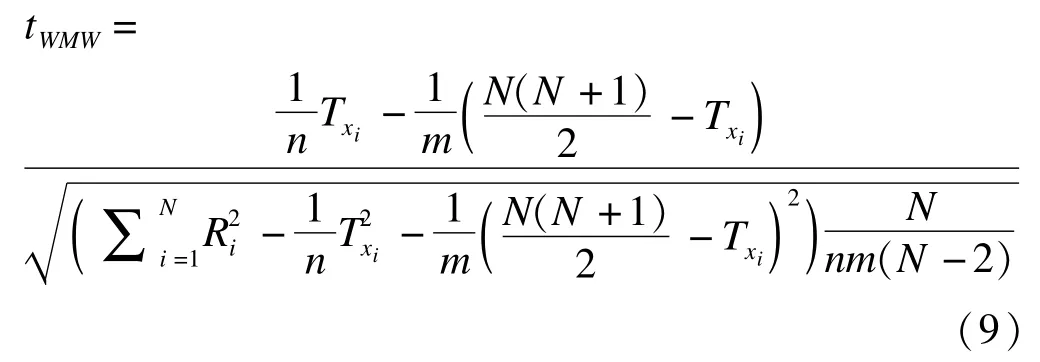
tWMW服从自由度υ＝N－2的t分布。

当不存在相同秩时，检验统计量ZWMW与tWMW有以下关系：

3.多个独立样本设计

非参数方法：（X11，X12，…，X1n1），（X21，X22，…，X2n2），…，（Xk1，Xk2，…，Xknk）表示k个独立随机样本，其样本量依次为n1，n2，…，nk，其中i≤k，j≤nk，即组数为k，第i组例数为ni，设Rij为k个样本数据混合后对应的秩次，即Rij的取值为1，2，…，N（N＝n1＋n2＋…＋nk），当观测值相等时，取平均秩次，可得Kruskal－Wallis（K－W）检验的统计量［8］：

秩转换类参数方法：用秩次Ri替代原始数据后采用方差分析，其检验统计量：

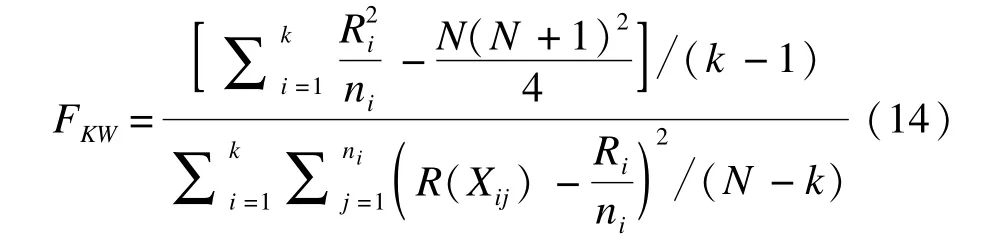
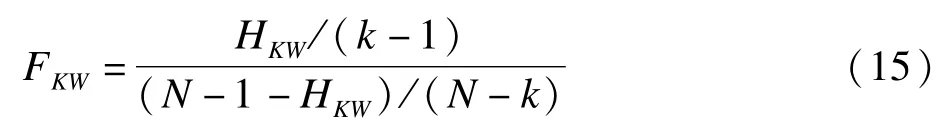
对上式（15）求HKW一阶导数，可证明FKW是一个关于HKW的严格单调递增函数。

模拟方法和结果

1.模拟方法及参数设置

模拟研究考虑分布、均数、方差和样本量等四个因素。因满足参数方法条件下（方差齐性和正态分布）已有结论，本模拟仅验证不满足参数方法的4种情形，即①左偏态分布（单样本）；②方差（两样本或多样本，后同）齐性且左偏态分布；③方差不齐且正态分布；④方差不齐且左偏态分布。样本量分别取5、6、8、10、12、14、16、20、25、30、35、40、50和100，有平衡和非平衡设计两种，后者两组样本量比例取1∶2。多个独立样本设计取3个水平。相同秩次均按平均秩次编秩。均数及方差的设置见后述。双侧检验，检验水准α＝0.05，模拟次数10000次。分别计算三种统计方法的I类错误率和检验效能。模拟过程采用R 3.1.0软件。

当方差不齐时，参数方法采用Welch校正。

2.结果

（1）左偏态分布

由图1可见，单样本或配对样本设计，参数方法的I类错误率明显大于秩转换类参数方法与非参数方法，而检验效能明显低于其他两种方法，其他两种方法的统计性能相近。

FKW服从自由度υi＝k－1，υ2＝N－k的F分布。

当无相同秩时，检验统计量HKW公式（12）与FKW公式（14）的关系如下：

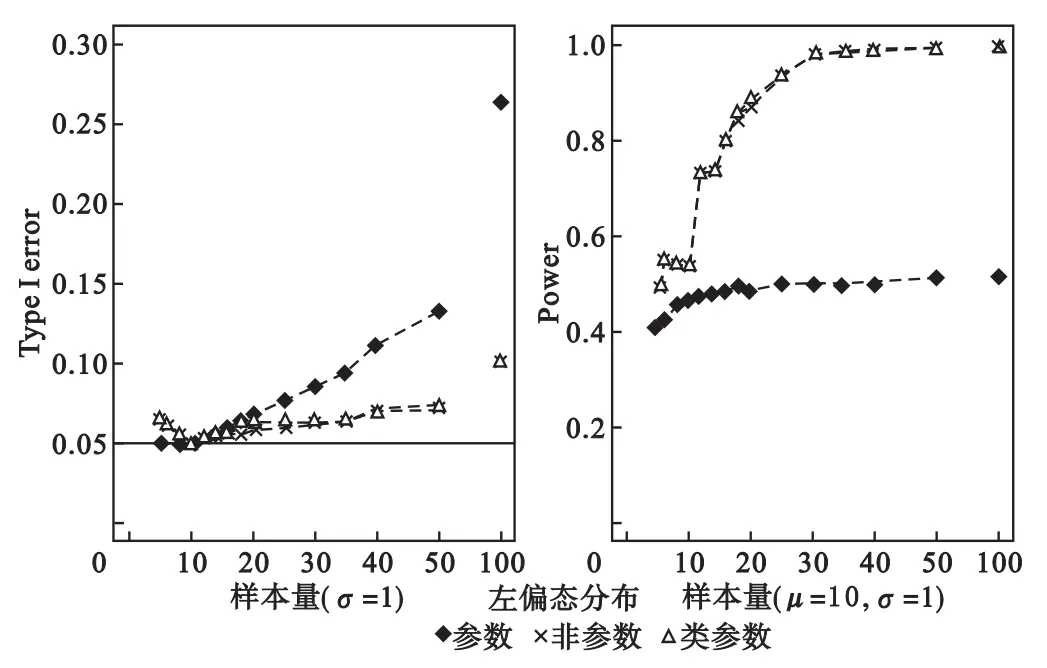
图1 左偏态分布单样本或配对样本

（2）方差齐性且左偏态分布

由图2可见，两独立样本设计，参数方法的I类错误率明显偏离且低于设定的检验水准0.05，检验效能亦明显低于其他两种方法，秩转换类参数方法与非参数方法的统计性能相近，并优于参数方法。三个独立样本设计的结果与两独立样本设计结果相一致。

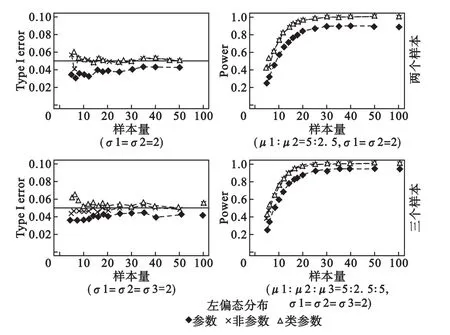
图2 左偏态分布且方差齐性（平衡设计）

（3）方差不齐且正态分布

由图3可见，对于I类错误率，当n≤20时，三种方法的波动幅度较大；当n＞20时，波动幅度明显减小，但均未增大趋势，以参数方法最接近设定的检验水准，秩转换类参数方法次之，非参数方法最差。对于检验效能，三种方法相近。

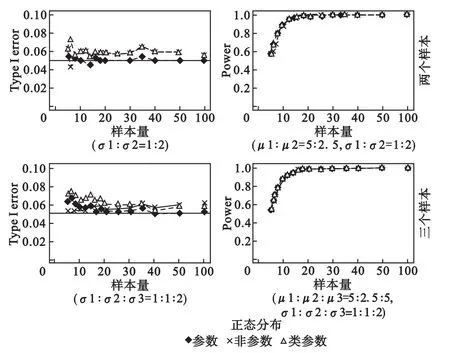
图3 正态分布且方差不齐（平衡设计）

（4）方差不齐且左偏态分布

由图4可见，对于I类错误率，参数方法较其他两种方法明显偏大，而且随样本量增大呈增大趋势；其他两种方法结果相近，接近设定检验水准。对于检验效能，参数方法偏低，其他两种方法相近。

非平衡设计的结果与平衡设计基本一致（因篇幅所限本文未给出）。

讨 论

对于满足参数方法条件的资料（正态分布和方差齐性），参数方法优于非参数方法和秩转换类参数方法已有公认结论，故本研究未考虑这一情形。本研究对于不满足正态分布的情况选择了一种左偏态分布，主要是考虑这种分布无法通过变量变换满足参数方法条件，虽然未考虑更多种类的非正态分布情形，但有代表性。

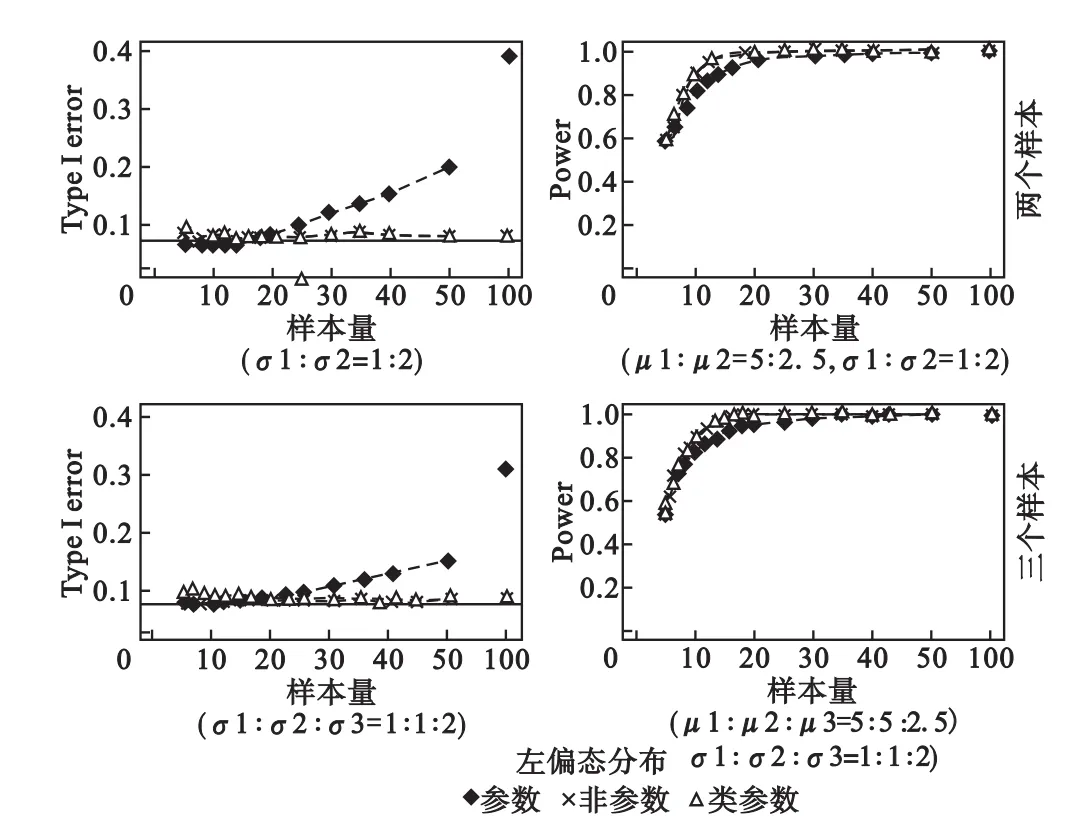
图4 左偏态分布且方差不齐（平衡设计）

对于单样本或配对样本设计，不服从正态分布的情形不宜使用参数方法，用非参数方法或秩转换类参数方法均可，且性能相近。

当方差不齐且服从正态分布时，参数方法的统计性能要优于其他两种方法，这一结果与赵景波等［9］和Skovlund等［10］的研究结果一致。因此，对于此类资料，尽管不满足参数方法的条件，但仍以选择经方差校正的参数方法为最佳选择。

当服从左偏态分布时，无论方差齐或不齐，参数方法的统计性能较差，不推荐使用。而非参数方法和秩转换类参数方法性能相近，均可使用。Zimmerman［11］对该两种方法进行了模拟比较，结果与本研究相似。

秩转换类参数方法实质上属于非参数方法，我们称之为“类参数方法”，是因为这是一种经过秩转换后使用常规参数方法的检验。虽然本研究所涉及的最常用的三种资料类型非参数方法和秩转换类参数方法性能接近，但我们所以进行秩转换类参数方法的研究，主要是考虑某些资料类型，如析因设计等较复杂设计目前尚无适用的非参数方法，这就为秩转换类参数方法应用的可能性提供了依据，也是我们的后续研究会进一步考虑的课题。

1.Rosner B.Fundamentals of Biostatistics.USA：Brooks／Cole 7th edit. 2011.

2.Friedman M.The use of ranks to avoid the assumption of normality implicit in the analysis of variance.Journal of the American Statistical Association，1937，32（200）：675-701.

3.Iman RL.A power study of a rank transform for the two-way classification model when interaction may be present.Canadian Journal of Statistics，1974，2（1-2）：227-239.

4.Iman RL，Hora SC，Conover WJ.Comparison of asymptotically distribution-free procedures for the analysis of complete blocks.Journal of the American Statistical Association，1984，79（387）：674-685.

5.Conover WJ，Iman RL.Analysis of covariance using the rank transformation.Biometrics，1982：715-724.

6.Conover WJ，Iman RL.Rank transformations as a bridge between parametric and nonparametric statistics.The American Statistician，1981，35（3）：124-129.

7.Conover WJ.Practical Nonparametric Statistics.New York：John Wiley，1980.

8.Kruskal WH，Wallis WA.Use of ranks in one-criterion variance analysis.Journal of the American statistical Association，1952，47（260）：583-621.

9.赵景波，李洪源，李康.两个非正态分布资料比较方法的选择.中国卫生统计，2003，20（3）：185-188.

10.Skovlund E，Fenstad G.Shold we always choose a nonparametric test when comparing two apparently nonnormal distributions.Joumal of Clinical Epidemiology，2001（54）：86-92.

11.Zimmerman DW.A note on consistency of non-parametric rank tests and related rank transformations.British Journal of Mathematical and Statistical Psychology，2012，65（1）：122-144.

（责任编辑：郭海强）

Practicability of Parametric Test Based on Rank Transform Statistic for Common Quantitative Data

Ye Yunshao，Chen Pingyan（Department of Bio-statistics，Southern Medical University（510515），Guangzhou）

ObjectiveTo explore the practicability of parametric test，nonparametric test and parametric test based on rank transformation for quantitative data of paired-sample（one-sample）designs，two independent sample designs as well as three or more independent sample designs when data violate normality or homoscedasticity.MethodsIntroducing the theory of parametric test based on rank transformation and comparing type I error and power of the three kind methods by means of Monte Carlo Simulation considering that data are normality or negative skewness and homoscedasticity or heteroscedasticity.ResultsThe results indicate that parametric test contributed to type I error inflations，of which type I error are clearly greater than nonparametric test and parametric test based on rank transformation no matter whether homoscedasticity or not.Parametric test is superior to two others when data are normality but heteroscedasticity.Nonparametric test has a good consistency to parametric test based on rank transformation in different designs.ConclusionType I error and power of parametric test based on rank transformation is nearly equal to that of the nonparametric test when data are applicable to nonparametric test.

Quantitative data；Parametric test；Nonparametric test；Rank transformation；Type I error；Power

*：国家自然科学基金项目（No.81273191）

△通信作者：陈平雁，E-mail：chenpy99＠126.com