视觉/惯性导航抗有色噪声滤波算法设计与仿真*



视觉/惯性导航抗有色噪声滤波算法设计与仿真*

周小刚，刘洁瑜，汪立新，熊陶，杨波

(第二炮兵工程大学，陕西 西安710025)

摘要：实际视觉/惯性组合导航中存在的噪声往往是相关的，必须考虑有色噪声影响，有色噪声的存在易导致视觉/惯性组合导航滤波算法的性能下降甚至发散。在分析视觉/惯性组合导航的结构组成和建立起系统状态方程的基础上，分别针对过程有色噪声和量测有色噪声情形，提出采用状态扩展法和量测状态扩展法对导航系统方程中的有色噪声进行处理，并以选定的优化准则进行滤波算法设计来解决有色噪声干扰问题。数值仿真实验证实所设计的抗有色噪声滤波方法性能稳定有效。

关键词：惯性导航系统；视觉；滤波；有色噪声

0引言

视觉(Vision)传感器可实时获取图像，并利用其来计算运动物体的运动参数，从而提供辅助导航信息。视觉导航是一个非常具有发展前景的导航方式。当前发展比较成熟的视觉导航技术有用于机器人的视觉导航技术、无人自主车、无人直升机的自主着陆控制技术等[1]。现阶段，国外视觉/惯性导航技术发展非常迅速。在高精度导航应用中，由于SLAM (simultaneous iocalization and mapping)系统的构建比较困难，视觉系统难以提供连续的导航定位信息，所以视觉系统通常被用来辅助GPS、惯性导航系统(inertial navigation system，INS)等导航系统[2-3]。Vision/INS导航在工业、军事、民用、科学研究等许多方面具有广泛的应用前景。

卡尔曼滤波算法是组合导航实际应用中最成熟的滤波算法，Vision/INS组合导航的滤波算法选择卡尔曼滤波无疑是最简便的，但是经典卡尔曼滤波应用的一个先决条件是已知噪声的统计特性，然而实际Vision/INS组合导航中受量测噪声、样本等方面限制，噪声的先验统计未知或不准确，这种情况下，采用经典卡尔曼滤波，易引起性能下降甚至发散。因此，必须针对Vision/INS组合导航的特点，设计具有抗噪声能力的滤波器。

1Vision/INS组合导航系统及其状态方程建立

1.1Vision/INS组合导航系统简介

视觉图像视觉导航依靠被观测图像框架在特定时间周期内的连续变换实现的。所需的传感器为相机，相机获取的特征参数通常可用于推理和确定连续图像框架间变化的数量。实现的方法通常有2种：第1种方法是基于光学流，试图建立三维空间图像框架间变化的模型。第2种方法是基于特征跟踪，该方法辨识图像中特征目标物体，并实现其在不同图像框架下的跟踪。基于光学流的方法主要为用户提供一些基本的运动参数估计，特征跟踪方法则通常应用于导航，用于判断被跟踪特征的距离范围[4]。视觉/INS结构示意图如图1所示。

利用一些方法可解决光学相机与期望特征目标的测距。这类操作类似于三角测量基线技术[5-6]。视觉图像传感器获得的特征图像是被观测目标的距离函数。一旦有特征目标被识别到，则立即进行特征关联处理以确定不同传感器观测到的为同一特征物体。假设特征关联时是静止的，而当其位置或者方位变化时，其与用户平台的位置和方位是相关联的。通过测得的已知信息即可实现某些运动参数的估计。

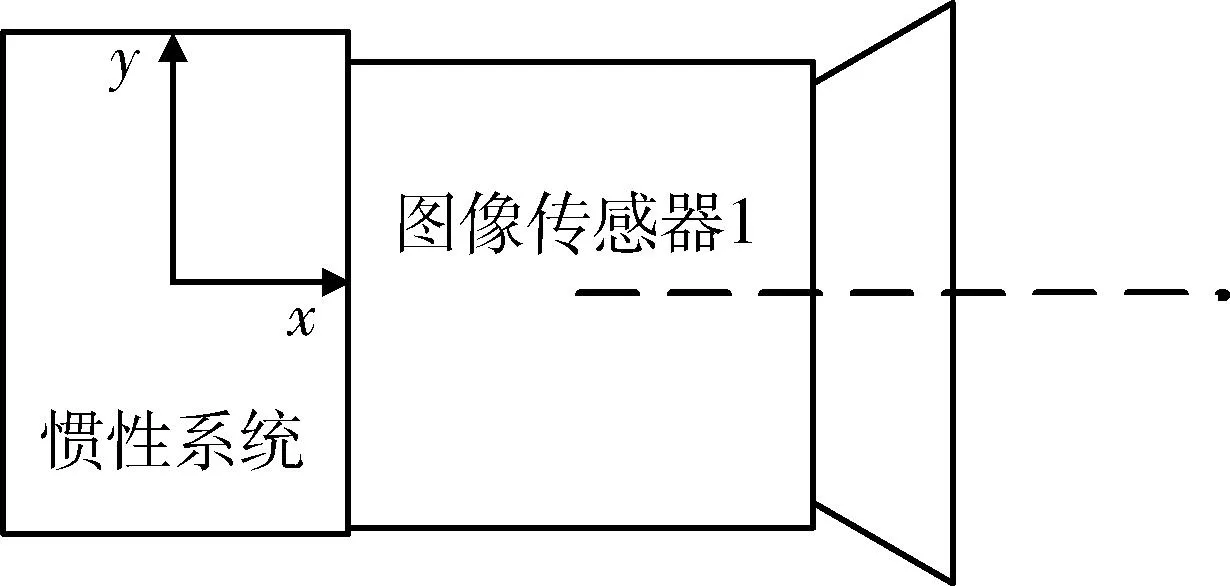
图1　视觉/INS结构示意图Fig.1　Vision/INS mechanization

1.2系统方程的建立

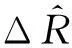
(1)

式中：li(tk)(i=1,2…,N)为tk时刻图像到传感器的距离信息，N为特征图像中的特征平面数。

由INS解算得到的位置变化信息如下：

(2)

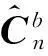
(3)

式中：φ为姿态角矩阵。

在tk时刻式(2)与(1)的差值：

(4)

通过变换，并考虑噪声ζ1影响，则上式可变换为

ZINS(tk)=Hp(tk)X(tk)+ζ1(tk)，

(5)

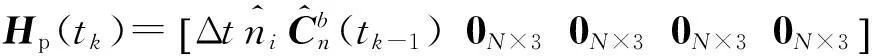
(6)

式中：X=(δx，δy，δz，δvx，δvy,δvz,δα,δβ,δγ，ωx0，ωy0，ωz0，fx0，fy0，fz0)T；δi(i=x,y,z)为位置误差；δvi(i=x,y,z)为速度误差；δα，δβ，δγ为姿态角误差；fi0(i=x,y,z)为加速度计零偏。

公式(5)和(6)可用于校正INS的位置和速度误差，但无法实现对姿态误差的估计，姿态误差估计可采用如下公式完成：

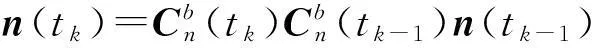
(7)

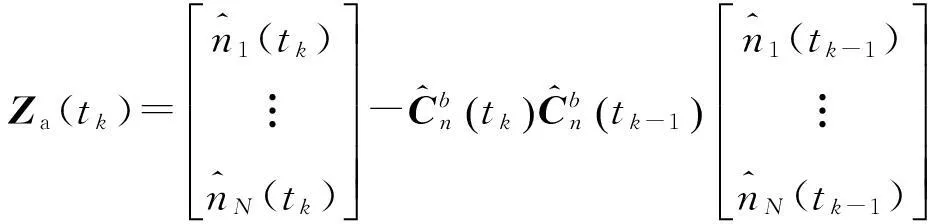
(8)

利用矢量间转换关系，可得

Za(tk)=Ha(tk)X(tk)+ζ2(tk),

(9)

式中：ζ2为噪声；

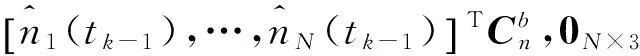
(10)

利用上述公式可建立具有如下形式的矩阵：

(11)

(12)

在满足香农定理条件下进行离散化，得离散方程：

Z(k)=H(k)X(k)+ζ(k).

(13)

系统的状态方程为

X(k)=Φ(k)X(k-1)+υ(k)，

(14)

式中：Φ(k)为状态转移阵；υ为过程噪声。

2抗有色噪声滤波器设计

2.1滤波稳定性判别

系统可看作为随机线性系统，根据滤波稳定性原理，如果随机线性系统是一致完全可控和完全一致完全可观测的，则滤波器是一致渐进稳定的[9]。显然，判断滤波器是否一致渐进稳定，只需判断原系统是否一致完全可控和完全一致完全可观测。对于式(13)和(14)组成的时变离散随机线性系统是否一致完全可控和完全一致完全可观测可分别按照能控性格拉姆矩阵判据和能观测性格拉姆矩阵判据[10]进行判断。通过分析知，式(13)和(14)组成的离散随机线性定常系统是稳定的。

2.2抗有色噪声滤波算法设计

视觉导航提供的信息非常丰富，然而这些信息中往往包括噪声成分，信号处理中的白噪声只是一种理论上假设的理想噪声，实际工程系统中的噪声总是相关的，只是在相关性比较弱的前提下近似的表示成白色噪声，而相关性比较强的条件下就必须考虑有色噪声影响，有色噪声的存在易导致滤波性能下降乃至发散，对此需要进行抗有色噪声滤波设计[11]。有色噪声主要包括过程有色噪声υ(k)和量测有色噪声ζ(k)2种，要通过滤波消除其中的1种或2种噪声，可采用如下方法进行设计。

对于存在过程有色噪声情况，采用状态扩充法，将状态方程中的有色噪声表达式转换成白噪声表示形式[12]。

令新的状态变量为

Xa(k)=(XT(k),υT(k))T.

过程有色噪声满足如下方程：

υ(k)=A(k,k-1)υ(k-1)+η(k-1),

(15)

式中：η(k-1)为白噪声，扩充后系统方程为

Xa(k)=Φa(k)Xa(k-1)+Γaη(k)，

(16)

Z(k)=Ha(k)Xa(k)+ζ(k)，

(17)

Γa(k,k-1)=(0，I)T，Ha(k)=(H(k)，0)。

此时，式(16)和(17)的系统方程将过程有色噪声转换为白噪声，如果系统中还包括量测有色噪声，则进一步对量测状态方程进行扩充。令新的状态变量：

Xb(k)=(Xa(k)，ζT(k))T，

量测有色噪声满足如下方程：

ζ(k)=φ(k,k-1)ζ(k-1)+μ(k-1)，

(18)

式中：μ(k)为白噪声。扩充后系统方程为

Xb(k)=Φb(k)Xb(k-1)+Γbηb(k),

(19)

Z(k)=Hb(k)Xb(k)，

(20)

至此，将有色噪声方程转换为白噪声方程(19)和(20)。在满足某种优化准则的条件下，可进行滤波器设计。上述过程对于仅含量测噪声情况，同样适用，这里以最小方差为准则，通过推导可得到如下滤波算法：

一步预测

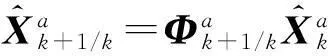
(21)

状态估计：

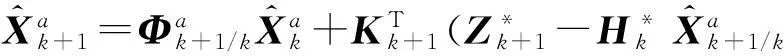
(22)

增益阵：

(23)

一步预测误差方差阵：

(24)

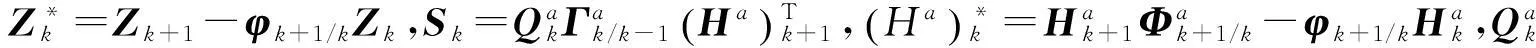
2.3滤波算法分析

前面滤波算法解决有色噪声干扰问题时，采用状态扩展和量测状态扩展的维数可达30+2N维，虽计算量较大，但求逆矩阵的维数与扩展前量测方程的维数2N相同，通过优先选择最佳匹配图像限制其值，可避免引起维数灾难，因此抗有色噪声滤波算法本身是可以实现的。

3数值实例

仿真仅考虑量测方程包含有色噪声情况，视觉/惯性组合导航系统装在载体上并以3×104m/s速度运动，所用INS的参数如下：陀螺零偏为0.1(°)/h，陀螺量测噪声N(0.001,(0.03)2)(°)/h，加速度计零偏为5×10-5g。采用的视觉传感器的测距绝对误差峰值2 cm，视觉图像传感器平面中心测量噪声(1)2cm，按照一定规律在量测方程中引入有色噪声，采样文中方法后滤波结果如图2所示。图中椭圆所圈部分为进行区域视觉导航误差修正段，进行误差修正后可有效消除累积误差，通过采用视觉导航前后对比不难得出：利用视觉导航信息后不仅可保证INS长行程和长时间的导航精度，而且系统具有较强的抗有色噪声能力。

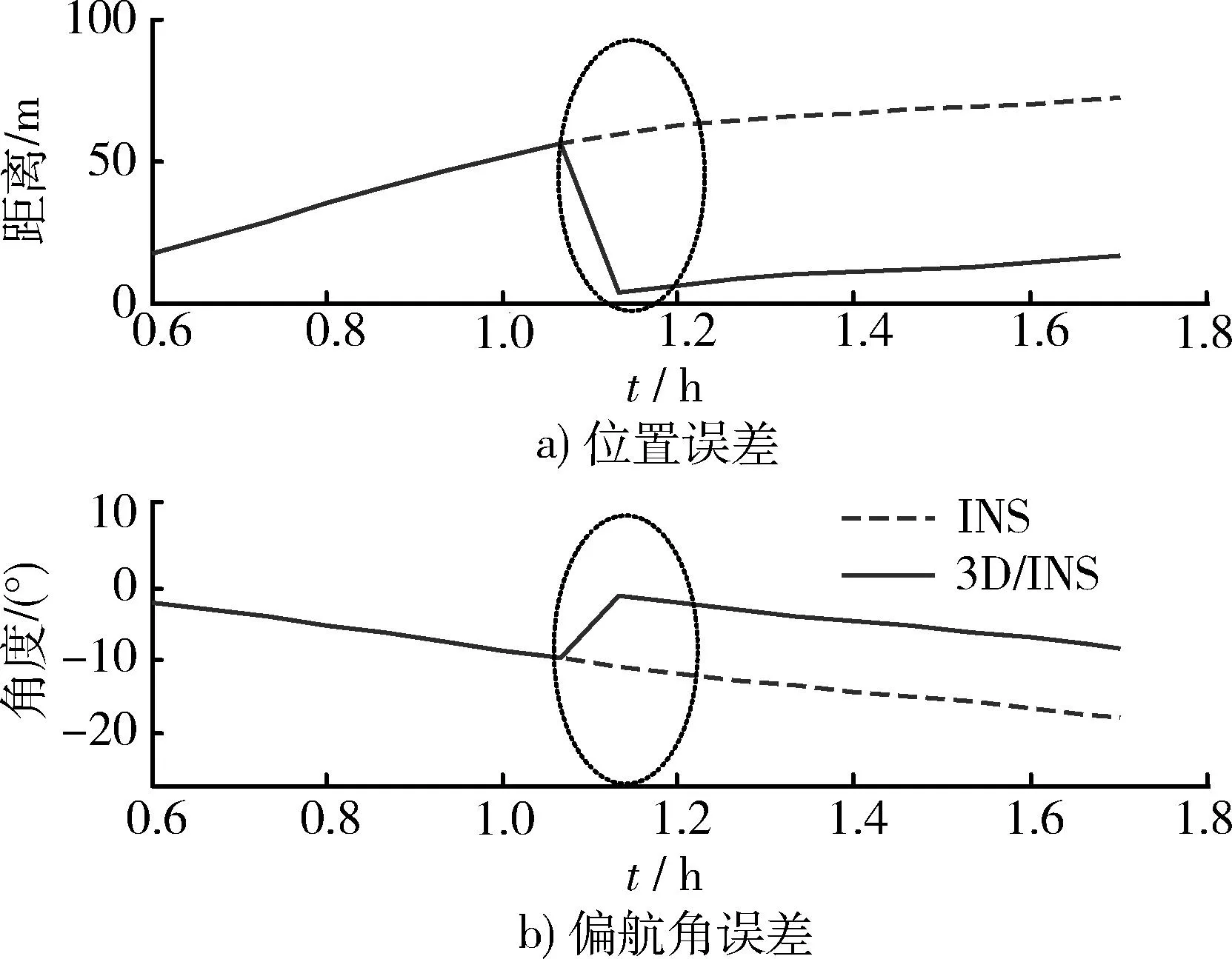
图2　Vision/INS导航抗有色噪声滤波仿真结果Fig.2　Vision/INS anti-colored noise filter　　　simulation result

4结束语

采用状态扩展法可对Vision/INS系统方程中的过程有色噪声进行滤波处理；采用量测状态扩展法则可对存在量测有色噪声进行有效处理。当2种有色噪声同时存在时，同时采用状态扩展和量测状态扩展方法可进行有效处理。系统仿真实验证实采用论文设计的抗有色噪声滤波方法能够保证Vision/INS系统的性能稳定。

参考文献：

[1]SUBRAMANIAN V.Development of Mchine Vision and Laser Radar Based Autonomous Vehicle Guidance Systems for Citrus Grove Navigation[J]. Computers and Electronics in Agriculture，2006,53(2):130-143.

[2]周小刚，汪立新,刘洁瑜,等.车载3D图像辅助导航系统研究[J].第二炮兵工程学院学报，2012,26(4)：28-31.

ZHOU Xiao-gang, WANG Li-xin, LIU Jie-yu,et al. The Car 3D Stereo-Vision Aid Navigation System Research[J].Journal of Second Artillery Engineering University, 2012，26(4)：28-31.

[3]Daniel Sullivan.High Accuracy Autonomous Image Georefereneing Using a GPS Inertial-Aided Digital Imaging System[C]∥Proeeedings of ION NTM，2002：1-6.

[4]BEIS J S, LOWE D G.Indexing Without Invariants in Vision Object Recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999(21):236-243.

[5]UIJT M, VENABLE D, SMEARCHECK M. Integration of an Inertial Measurement Unit and Vision Imaging Sensor for Urban and Indoor Navigation of Unmanned Vehicles[C]∥Proceedings of the National Technical Meeting of the ION, January, 2007：22-24.

[6]丁少文，王林.基于连续三角测量法的机器人定位方法[J].微型电脑应用，2013,30(5)：76-80.

DING Shao-wen, WANG Lin, One Mobile Robot Localization Method Based on Continuous Triangulation[J], Microcomputer Applications, 2013,30(5)：76-80.

[7]Evan T Dill. Integration of Vision and 2D Imaging Data for Assured Navigation in Unknown Environments[D].The Russ College of Engneering and Technology of Ohio University, 2011.

[8]周小刚，刘洁瑜，汪立新,等.车载3D立体视觉辅助惯性导航与仿真实验研究[J]，现代防御技术，2013，41(5)：36-40.

ZHOU Xiao-gang, LIU Jie-yu, WANG Li-xin,et al.Vehicle Mounted 3D Stereo Vision Aided IMU Navigation System and Simulation Experiment[J].Modern Defence Technology, 2013，41(5)：36-40.

[9]宋国东，姜守达，林连雷.复杂有色噪声广义系统信息融合Kalman滤波器[J].仪器仪表学报，2013，34(5)：107-110.

SONG Guo-dong, JIANG Shou-da, LIN Lian-lei.Information Fusion Kalman Filter with Complex Colored Noise for Descriptor Systems[J]. Chinese Journal of Scientific Instrument, 2013，34(5)：107-110.

[10]许涛，祝小平,杨军.有色噪声条件下的目标被动定位算法研究[J].计算机仿真，2013，30(5)：67-71.

XU Tao,ZHU Xiao-ping, YANG Jun.Research on Passive Location Algorithm for Colored Measurement Noise[J].Computer Simulation, 2013，30(5)：67-71.

[11]赵琳.非线性系统滤波理论[M]. 北京：国防工业出版社，2012.

ZHAO Lin. Nonlinear System Filter Theory[M].Beijing:National Defense Industry Publishing Company,2012.

[12]郑大钟.线性系统理论[M].北京：清华大学出版社，2002.

ZHENG Da-zhong. Linear System Theory[M].Beijing:Tsinghua University Press,2002.

Design of Anti-Colored Noise Filter for Vision/INS Integrated Navigation System and Simulation Experiment

ZHOU Xiao-gang，LIU Jie-yu, WANG Li-xin, XIONG Tao, YANG Bo

(The Second Artillery Engineering University,Shaanxi Xi′an 710025, China)

Abstract:The filtering algorithm performance of vision/INS usually declinesand even scattersdue tosystem colored noise. The methods of state extended and measurement state extended areput forward to solve the problems of processing and measuringcolored noise based on analyzing the composition of vision/INS and building the state equation. The filer algorithm is also designed by using the selected optimization rules. The simulation experiment proves that the method mentioned above is stable and valid.

Key words:inertial navigation system；vision；filter；colored noise

中图分类号：V448.122；TP391.9

文献标志码：A

文章编号：1009-086X(2015)-02-0199-04

doi:10.3969/j.issn.1009-086x.2015.02.032

通信地址：710025西安第二炮兵工程大学304教研室E-mail：sheqiangzhou@163.com

作者简介：周小刚(1979-)，男，四川南充人。讲师，博士后，研究方向为惯性技术与信号处理。

基金项目：校青年基金(XY2011JJB20)

* 收稿日期：2014-03-22；
修回日期：2014-05-20