基于两级联合库存的低消耗备件优化配置研究*
2015-03-09董琪,徐廷学,杨继坤等
基于两级联合库存的低消耗备件优化配置研究*
董琪a,徐廷学b,杨继坤a,赵建忠b
(海军航空工程学院 a.研究生管理大队; b.兵器科学与技术系,山东 烟台264001)
摘要:针对现行装备低消耗备件供应保障效率不高的问题,提出了基于两级联合库存的低消耗备件优化配置方法。在建立备件两级联合库存模型的基础上,引入备件横向调拨策略,并以横向调拨方案为约束条件,两级库存系统期望缺货量最少、横向调拨量最大为优化目标,建立了两级联合库存配置优化模型。运用线性规划软件对模型进行求解和优化,结合实例对横向调拨方案进行了分析,结果表明该模型在达到备件配置要求的情况下,提高了备件利用率,为制定合理的备件优化方案提供决策依据。
关键词:联合库存;低消耗备件;优化配置;横向调拨
0引言
备件的横向供应理论和库存优化模型是装备综合保障领域新兴的热点问题,不仅直接影响着装备全寿命周期费用,还直接影响装备的战备完好性及其作战能力[1]。目前,尽管GJB4355《备件供应规划要求》对部队备件保障模式包括上下级备件供应和同级仓库备件横向供应做了明确的规定,但在备件实际保障过程中,同级仓库间极少进行横向供应。但当发生备件短缺时,距离较近的同级仓库间的补给要比上一级仓库补货更加经济、快捷。特别是对于年需求量小于4件的低消耗备件而言[2],各仓库的库存量均不多,避免因积压造成浪费,但也会因需求突然增加出现仓库缺货的情况。因此,在这种较为复杂的备件供应模式下,为了保证装备备件最小的库存缺货,最大限度的提高装备保障效率,需要在各级仓库之间建立合理的库存调拨策略。
对于联合库存和横向调拨模型研究,文献[3-5]研究了多个维修站的维修备件联合库存优化问题。文献[6]研究了以库存持有成本、缺少备件导致的停机损失成本和横向转借成本之和为目标函数,以系统的备件需求满足率为服务水平约束的多仓库联合库存优化模型。文献[7]研究了有横向紧急供应策略下的单级库存模型。文献[8]对多级多品种低需求服务备件库存系统进行了研究,并建立了以顾客的最大等待时间为约束,以系统总库存成本为目标的规划模型。
尽管上述研究取得了一定的成果,大多数国内外学者理论研究的对象通常是商业供应链,其供应模式与部队现有保障模式存在一定的差异。针对海军装备备件保障实际模式,研究了一个由舰队级仓库和多个基层级仓库组成的备件库存系统,正常情况下,基层级仓库由舰队级仓库供应备件,当发生库存短缺时,各基层级仓库允许横向调拨和从舰队级仓库补货,建立了允许横向调拨的两级备件联合共享模型,利用线性规划软件Lingo对模型进行求解。通过实例验证表明,合理的联合库存模型和横向调拨模型可以提高备件利用率和装备保障水平,减少备件短缺概率,为装备保障建设提供决策支持。
1问题描述和基本假设
1.1问题描述
在研究低消耗备件的两级联合库存决策时,可以将舰队级仓库和此仓库供应下的各基层级仓库视为一个两级联合库存系统,如图1所示。具体描述如下:假设两级库存系统中共有n-1个基层级仓库和1个舰队级仓库,系统中只有各基层级仓库对备件有需求。在实施备件共享后,两级联合库存系统的备件配置目标应优先满足军事目标,即最大限度地满足需求较高的基层级仓库,同时每个基层级仓库都可以获得尽量多的支援,使得两级联合库存系统的缺货量最小,装备的可用度最高。由于不同的备件调拨策略会影响备件配置优化目标,因此,影响低消耗备件两级联合库存系统配置优化模型的约束条件是制定何种备件横向调拨策略以达到配置目标。
1.2基本假设
根据上述分析,可将两级联合库存系统看作一个多点库存转运系统,其假设如下:
(1) 备件Ω为可修复备件,其维修过程即为备件的周转过程;
(2) 各基层级仓库对备件Ω的需求服从独立的泊松分布;
(3) 为应对不确定需求,该两级库存系统设置安全库存,并存放在舰队级仓库;
(4) 在满足该两级库存系统备件满足率要求时,n-1个基层级仓库共需备件Ω被分配至各基层级仓库;
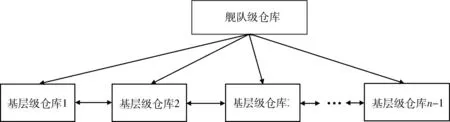
图1 低消耗备件联合库存系统Fig.1 Joint stock system of low consumption spare parts
(5) 各基层级仓库和舰队级仓库完全共享备件Ω,各基层级仓库之间可相互支援调拨,舰队级仓库可向各基层级仓库调拨;
(6) 忽略2个以上基层级仓库同时缺货且同时需要支援的情况,假设每次需要支援调拨的基层级仓库数只有1个;
(7) 进行支援调拨时,由于可能会有2个或者更多可供选择的转运源,则需要明确转运点的选择原则,本文采取就近原则;
(8) 各基层级仓库和舰队级仓库中任一库存的备件Ω都能满足需求方对它的质量水平要求、供货时间(备运期)要求等。
图2所示为本文研究思路及流程。

图2 研究流程图Fig.2 Flow chart of the research
2模型构建
2.1模型参数定义及符号说明
R:n个基层级仓库对低消耗备件Ω总需求数的随机变量;
Ri:各基层级仓库对备件Ω需求数的随机变量;
μ:联合库存系统的总需求量均值;
μi:舰队级仓库和各基层级仓库的供应周期需求均值,其中i=1,2,…,n;
σ2:联合库存系统总需求量的方差;
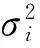
S:n-1个基层级仓库共需备件Ω的数量;
Si:各基层级仓库的库存量;
EBO:库存系统期望缺货量;
ss:安全库存量;
α:两级库存系统备件满足率;
αji:仓库j向仓库i支援调拨的支援系数;
xji:仓库j向仓库i调拨的备件数;
λ:联合库存系统年需求均值;
λi:各基层级仓库年需求均值;
Z:备件供应良好率下的安全库存系数;
tji:仓库j向仓库i发出支援调拨的时间;
λg:订货间隔期需求均值。
2.2联合库存模型
采取联合库存管理时,各基层级仓库和舰队级仓库实施联合库存,将n个基层级仓库和一个舰队级仓库视为一个整体,且整体的备件需求服从泊松分布,其需求均值是各仓库需求均值之和,需求方差小于或等于各仓库需求方差的和,且只有在n个基层级仓库的需求方差均相同时等式成立。证明如下:
若已知备件Ω在各基层级仓库的需求服从泊松分布,则n个基层级仓库对备件Ω的总需求也服从泊松分布,证明过程见文献[9]。其需求数的数学期望值为
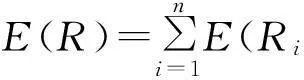
(1)
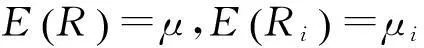
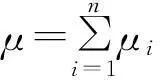
(2)
假设各基层级仓库对备件Ω的需求相互独立,而n个基层级仓库总需求量的方差为
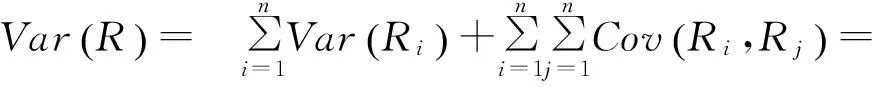
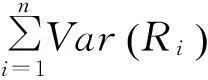
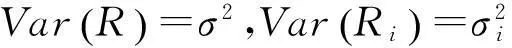

于是,

(3)
式(3)表明,在采取相同服务水平的情况下,n个基层级仓库集中订货比各基层级仓库分散订货的订货量小[10]。因此,在实际备件配置中,且相同的备件满足率下,各基层级仓库对装备备件的需求方差一般不相同,在采取联合库存需要的总库存量一般小于各基层级仓库独立库存的库存量之和。
于是,建立备件满足率不小于α的联合库存模型:
(4)
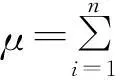
由联合库存模型计算得到的备件数量S,即在备件满足率α下两级库存系统所需备件Ω的总库存量。
2.3基于横向调拨的配置优化模型
在实施备件联合库存后,可通过建立备件配置优化模型,解决联合库存策略下两级库存系统关于低消耗备件的分配问题。本文研究备件配置优化的目标之一是库存系统期望缺货量最小,库存系统期望缺货量可表示为
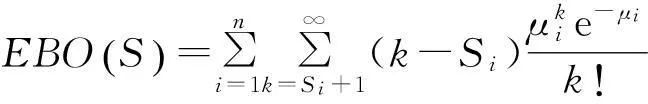
(5)
由式(5)可知,库存系统期望缺货量由各仓库库存量和需求概率均值2因素决定。因为各仓库需求概率均值可通过调研求得,因此,各仓库库存分配量是库存系统期望缺货量的决策因素。
本文在基础上考虑了基层级仓库备件横向调拨情况,结合库存系统备件配置优化目标为基层级各仓库获得调拨总量最大,两级联合库存系统的缺货量最小,可建立基于横向调拨的配置优化模型目标函数:
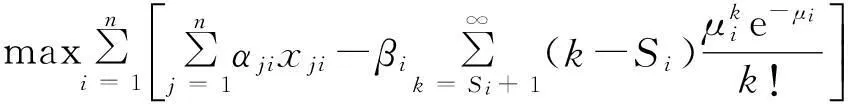
(6)
影响优化模型取值的变量为αji,βi,xji,Si,其中αji和βi由各仓库的地理位置和需求稳态概率均值决定,而可xji和Si的取值范围根据调拨策略而定,备件横向调拨策略如下:
(1) 各基层级仓库在获得分配之前备件Ω的库存为0,且各基层级仓库对备件Ω的库存限额为5;
(2) 库存不小于l件的仓库允许有多种向外支援调拨的方案可供选择,每件备件Ω都有1~2种对外支援的方案;
(3) 所有基层级仓库在获得分配后备件Ω的库存总数为S;
(4) 仓库j向仓库i的调拨量为1
根据以上调拨策略可构建配置优化模型关于决策变量的约束条件为
(7)
式中:i=2,3,…,n;j=1,2,…,n.
除横向调拨策略外,由于舰队级仓库作为后方仓库具有缓冲库存的作用,应设置安全库存。另外,在备件正常调拨中,不允许备件从基层级仓库逆向调拨回舰队级仓库,因此构建约束条件如下:
(8)
式中:j=1,2,…,n。
综合式(4)~(8)得到基于横向调拨的低消耗备件联合库存配置优化模型。
3模型求解
3.1安全库存量计算
为应对低消耗备件两级库存系统中预料之外的备件需求,一般要考虑设置系统的安全库存(又称为缓冲库存)。在备件两级库存系统中,若备件两级库存系统对某项备件总的需求服从泊松分布,库存系统年需求均值为各基层级仓库年需求均值之和,即
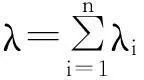
(9)
若已知备件Ω的送修周期为T天,则订货间隔期内备件Ω的需求均值为
λg=λT/365,
(10)
且送修间隔期内的需求标准差为送修间隔期需求均值的平方根[11],即
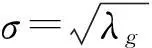
(11)
则库存系统的安全库存量可表示为

(12)
式中:Z可由正态分布表查得[12]。
3.2调拨系数计算
两级联合库存系统中,基层级间横向调拨发生在某仓库i因缺货且不能得到及时补充时,由库存不为0的仓库j发出支援调拨,且各仓库相互间的支援能力不与本仓库的备件需求率相关,只与相互间的调拨时间有关[13]。因此,取调拨系数的值为调拨时间的倒数。若仓库j向仓库i发出支援调拨的时间为tji,则仓库j向仓库i的调拨系数为1/tji,归一化处理后得
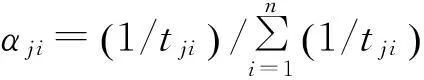
(13)
3.3缺货系数计算
βi表示仓库i的缺货系数,与本仓库的稳态需求概率均值相关,其取值为

(14)
3.4配置优化模型求解方法
低消耗备件配置优化模型有2组决策变量,分别是各基层级仓库获得分配的库存量S、各基层级仓库及舰队级仓库互相支援调拨的调拨量xji。线性规划软件Lingo数学软件是常用的解决优化问题的软件之一。所以,本文采用Lingo软件来进行仿真实验,求解此模型。
4实例分析
某两级库存系统中有7个基层级仓库(代码分别为a,b,c,d,e,f,g)和1个舰队级仓库(代码为z),且这7个基层级仓库对某型部件均存在备件需求。各基层级仓库的备件需求情况如表1所示。其中,年需求均值为mi,修理周期需求均值为μi。

表1 各基层级仓库对某型备件的需求统计数据
经调研得到7个基层级仓库之间的调拨时间及舰队级仓库至基层级仓库的供应时间tji,单位为天,如表2所示。由于基层级仓库对舰队级仓库不进行调拨,以及各基层级仓库对自己无需调拨,因此用“—”表示。
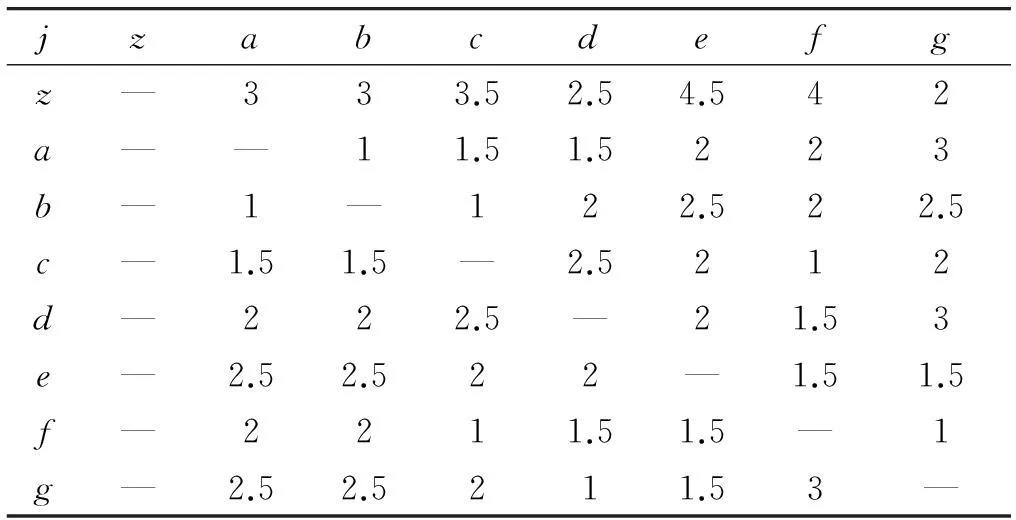
表2 各仓库之间的支援调拨时间
已知该型部件的订货间隔期为1年,送修周期为45天,要求送修周期内的备件满足率不低于90%的条件下,用两级联合库存模型求解舰队级仓库和7个基层级仓库对该备件总的库存需求量、库存配置策略及横向调拨策略。
4.1联合库存系统需求量求解
(1) 基层级库存需求量计算
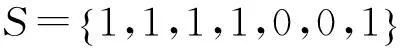
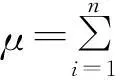
由此得出,实施备件共享策略可使该两级库存系统节约备件3件。
(2) 舰队级仓库安全库存量求解
在联合库存策略下,7个基层级仓库和一个舰队级仓库组成的两级库存系统集中组织对该型备件的订货,根据公式(9),(10)和(11),则送修间隔期内的需求均值为λg=10.4,送修间隔期内的需求标准差为σ=3.2。
若要求该备件的供应良好率为90%,查正态分布表得Z=1.04,由公式(12)得,该库存系统对该型备件总的安全库存为ss=3.33,取整后得ss=4。
综上,该两级库存系统在联合库存策略下,若考虑安全库存,共需要该型备件6件,其中2件分配至各基层级仓库,4件作为安全库存存储在舰队级仓库。
4.2联合库存系统横向调拨参数计算
(1) 计算调拨系数
由式(13)可求得调拨系数αji,对于不发生调拨的,取调拨系数为0,由此得各仓库间的调拨系数如表3所示。
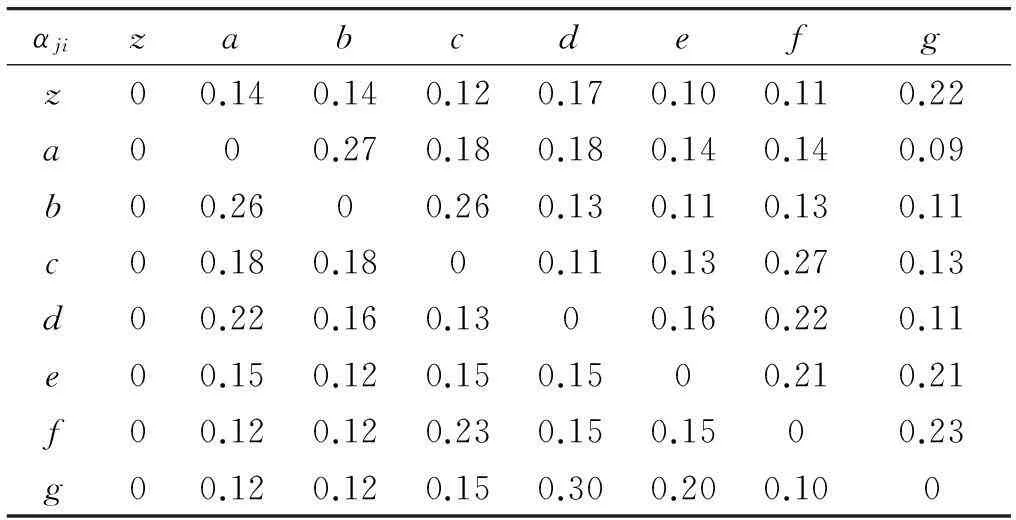
表3 各仓库之间的调拨系数
(2) 计算缺货系数
由式(14)可求得各仓库的缺货系数如表4所示。

表4 各仓库的缺货系数
4.3配置优化模型求解
(1) 模型求解
利用Lingo软件编程并运算,得到备件配置结果如表5所示。

表5 备件配置结果
(2) 横向调拨方案分析
在横向调拨策略下,每一件库存备件都有一个或两个调拨方向,实际应用中可根据需要进行选择。求解得到的横向调拨方案如表6所示。
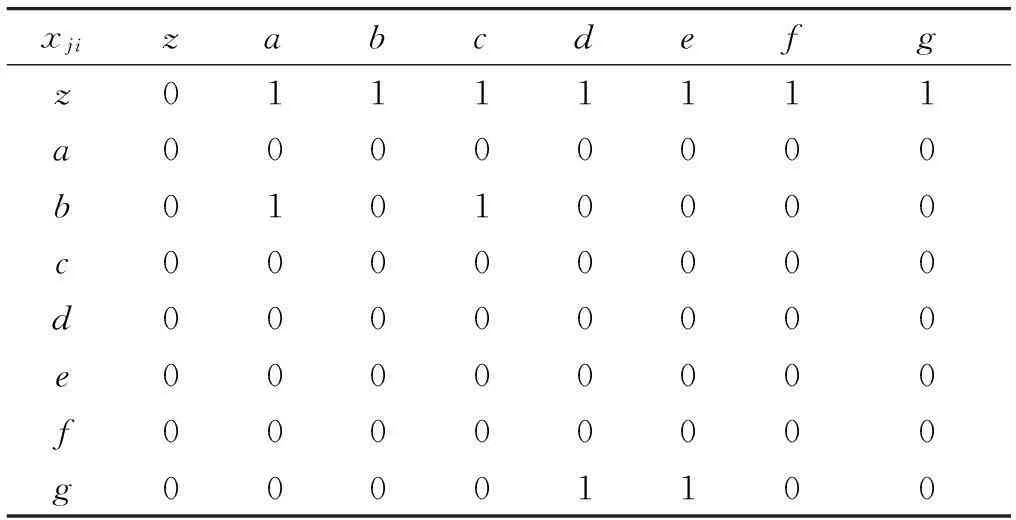
表6 各仓库之间的支援调拨方案
模型中假设每件备件可有1~2种支援调拨方案,得到的所有调拨方案如图3所示。

图3 调拨方案Fig 3 Allocation program
1) 舰队级仓库有下列调拨方案:舰队级仓库→基层级仓库a、舰队级仓库→基层级仓库b、舰队级仓库→基层级仓库c、舰队级仓库→基层级仓库d、舰队级仓库→基层级仓库e、舰队级仓库→基层级仓库f、舰队级仓库→基层级仓库g。因为舰队级仓库有4件该型备件,则舰队级仓库可任意选择其中1~4个路径进行调拨;
2) 基层级仓库b的调拨方案:基层级仓库b→基层级仓库a、基层级仓库b→基层级仓库c;
3) 基层级仓库g的调拨方案:基层级仓库g→基层级仓库d、基层级仓库g→基层级仓库e。
4.4结果分析
从分配结果可以看出,在对7个基层级仓库分配2件该型备件时,首先需求率最高的基层级仓库b得到了一件备件分配,这就在一方面满足了高需求仓库能够优先得到库存满足这一要求;同时,基层级仓库g因为在对基层级仓库d和基层级仓库e进行调拨时所需的调拨时间最短,所以,为了能够快速应对基层级仓库d和基层级仓库e的需求,将另一件备件分配至基层级仓库g,这就满足了备件调拨的目标要求。
从表5库存分配结果及表6支援调拨方案可以得出,在联合库存策略下,各基层级仓库对于该型备件有2种获取途径:一是本仓库的库存;二是其他仓库的支援调拨。在充分共享策略下,假设每件备件都有1种或2种调拨路径可供选择,各基层级仓库最多可获得的备件数如表7所示。

表7 联合库存策略下各基层级仓库最多可获得的备件数
5结束语
本文从低消耗备件保障实际出发,对一个舰队级仓库及多个基层级仓库组成的两级库存系统进行了研究。通过分析横向调拨策略,建立了库存配置优化模型,结合实例运用线性规划软件对模型进行验证。计算得到的优化结果满足了两级联合库存系统调拨总量最大,缺货量最小的配置要求,快速应对了缺货仓库的备件需求。相比采取独立库存策略的库存系统,以及未采取横向调拨策略的库存系统,本文研究的模型提高了低消耗备件利用率和供应水平,为装备保障备件供应规划提供一定的决策依据。
参考文献:
[1]张光宇,李庆民,郭璇.基于横向转运策略的可修备件多点库存建模方法[J].系统工程与电子技术,2012,34(7):1425-1429.
ZHANG Guang-yu, LI Qing-min, GUO Xuan. Modeling for Repairable Spare Parts in Multi-Location Inventory System with Lateral Transshipments [J]. Systems Engineering and Electrionics, 2012, 34(7):1425-1429.
[2]Jeffrey J Hobbs. Analysis of Low Demand Items [M]. New York: Department of Defense Logistics, 1996.
[3]WONG H, HOUTUM V G J, CATTRYSSE D, et al. Multi-Item Spares Systems with Lateral Transshipments and Waiting Time Constraints[J]. European Journal of Operational Research, 2006(3): 1071-1093.
[4]杨华,郭伟,毕海玲.大型设备制造企业维修备件联合库存优化研究[J].中国机械工程,2009,20(15):1802-1806.
YANG Hua, GUO Wei, BI Hai-ling. Research on Pooling Inventory Optimization for Large Equipment Manufacturer’s Maintenance Parts [J]. China Mechanical Engineering, 2009, 20(15): 1802-1806.
[5]张琳,赵杰,唐超,等.可维修备件库存模型研究[J].兵工学报,2009,30(11):90-94.
ZHANG Lin, ZHAO Jie, TANG Chao, et al. Research on the Echelon Inventory Model of the Repairable Spares [J]. Acta ArmamentarII, 2009, 30(11): 90-94.
[6]许民利,孙彩群.基于等待时间限制的服务备件多点转运库存模型研究[J].山东大学学报:理学版,2010,45(3):61-65.
XU Min-li, SUN Cai-qun. A Multi-Location Inventory Model for Service Parts with Lateral Transshipment and Waiting Time Constraints [J]. Journal of Shandong University:Natural Scienceed, 2010, 45(3): 61-65.
[7]KRANENBURG A A,HOUTUM V G J.A New Partial Pooling Structure for Spare Parts Network[J].Journal of Operational Research, 2009(3):908-921.
[8]JAYARAMAN V, PIRKUL H. Planning and Coordination of Production and Distribution Facilities for Multiple Commodities [J]. European Journal of Operational Research, 2001(2): 394-40.
[9]Sherbrooke Craig C. Optimal Inventory Modeling of Systems: Multi-Echelon Techniques [M]. New York:Springer Science Business Media, 2004.
[10]王晶,方建奇,仇晨,等.连锁经营企业集中订货与支援调拨策略及模型[J].工业工程,2005,8(2):11-16.
WANG Jing, FANG Jian-qi, QIU Chen, et al. Policy and Model of Group Ordering and Resource Allocating for Chain Stores [J]. Industrial Engineering Journal, 2005, 8(2): 11-16.
[11]WANG Y Z, COHEN M A, ZHENG Y S. Differentiating Customer Service on the Basis of Delivery Lead-Times [J]. IIE Transactions, 2002(34): 979-989.
[12]Abdul-Jalbar B,Gutierrez J,Puerto J, et al. Policies for Inventory Distribution Systems: the Effect of Centralization vs Decentralization [J]. International Journal of Production Economics, 2003(3):281-293.
[13]WONG H, CATTRYSSE D, OUDHEUSDEN D V. Stocking Decision for Repairable Spares Pooling in a Multi-Hub System [J]. International Journal of Production Economics, 2005(3): 309-317.
Optimization of Low-Consumption Spares Supply Based on Two-Echelon Joint Inventory
DONG Qia, XU Ting-xueb, YANG Ji-kuna, ZHAO Jian-zhongb
(Naval Aeronautical and Astronautical University, a. Graduate Students’ Brigade;b.Department of Ordnance Science and Technology, Shandong Yantai 264001,China)
Abstract:Focusing on low support effectiveness of low-consumption spares, the optimization inventory approach of low-consumption spares for two-echelon joint inventory is presented. Based on two-echelon inventory-share model, optimization model of low-consumption spares is established withthe introduction of lateral transfers strategy, the maximum transfer spares, the minimum shortage as target and lateral transfers schemes as constraint conditions. In the case, optimization model is solved by Lingo, and lateral transfers schemes is analyzed. The result can not only satisfy the support optimization target but also improve utilization rate of spare parts, which has a large significance for supplying decision assistance for a reasonable optimization project.
Key words:joint inventory; low-consumption spares; spare optimization; lateral transfers
中图分类号:TJ760.7;
文献标志码:A
文章编号:1009-086X(2015)-02-0165-07
doi:10.3969/j.issn.1009-086x.2015.02.027
通信地址:264001山东烟台海军航空工程学院研究生1队E-mail:lance0627@163.com
作者简介:董琪(1986-),男,河南平顶山人。博士生,主要从事装备综合保障研究。
* 收稿日期:2014-05-26;
修回日期:2014-07-08
