复杂腔体电磁混沌特性统计分析

庄信武 余志勇 刘光斌 滕向如 陈 亮

（第二炮兵工程大学，陕西 西安710025）

引 言

电大尺寸特征结构的复杂腔体内的场，往往具有较强的边界敏感性或不确定性，很难对下一状态进行有效的预测，这反映了电大尺寸结构的不可积性质.通常将这种不可积称为电磁混沌特性［1］.目前主要从三种方法来描述复杂腔体内电磁波的混沌特性：1）利用粒子射线轨迹分布图来描述场的混沌特性［2-3］.该方法将电磁场视为由无限多个、各向同性、互相独立的粒子组成，粒子的运动轨迹特征表征了场的统计特性，若射线轨迹越具有遍历性，则腔体就越混沌.但该方法仅考虑了腔体的内部几何结构对粒子射线轨迹遍历性的影响，而忽略了腔体材料属性的影响；2）利用归一化最近相邻本征模间隔分布来描述场的混沌特性［4］.若复杂腔体内场的归一化最近相临本征模间隔趋近于指数分布，则为可积的；若复杂腔体内场的归一化本征模间隔接近于Wigner分布，则为混沌的.而现实复杂腔体的归一化本征模间隔往往介于混沌与可积系统之间，此时场的混沌特性如何评估有待于解决；3）利用混响室内场的统计理论来描述场的混沌特性［5-6］.当腔体激励模达到过模状态时，即混响室内场满足各向同性、均匀分布、随机极化的要求，混响室内场可视为混沌状态.

综上，目前对电大尺寸腔体内场的混沌性评估没有给出明确指标，更多是从场的幅值、幅值均方等方面展开统计特性研究［7-9］.因此，为了更好地评估腔体的混沌特性，并扩展其运用，文章将基于量子力学中的Schrödinger方程与电磁学的Helmholtz方程的相似性原理［10］，采用量子混沌理论，定量地研究腔体内场的混沌特性.

1 理论分析

量子混沌理论是模式理论研究的重要内容，是电磁学关于场混沌特性研究的重要工具，主要包括模式密度、本征频率、模式间隔分布等.

1.1 模式密度分析

模式密度分布规律与腔体的形状、本征频率的分布有关.若本征频率越低，则模式密度就越依赖于腔体的几何结构特征，特别当本征频率低于最低可用频率时，这种依赖性就更明显.Weyl为此总结了无损腔体模式密度的分布规律：若腔体内部分段边界是光滑的，则任意无损腔体的平均光滑累积模式密度为［11］

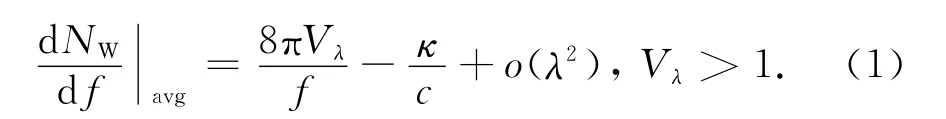
式中：f为本征频率；Vλ＝V／λ3为电尺寸（λ表示本征频率处的信号波长，V为腔体体积），通常将符合Vλ≫1条件的结构称为电大尺寸结构；c为光在腔体媒质中的传播速度；κ为几何因子，

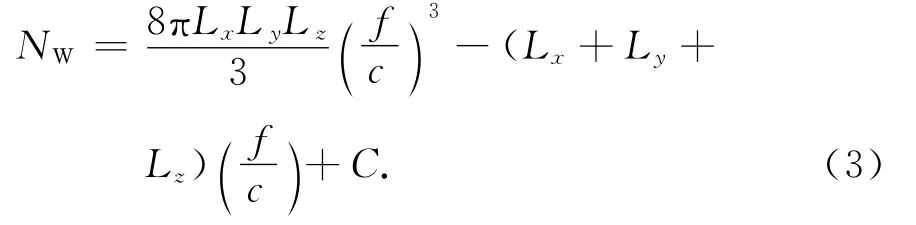
式中：Lx、Ly、Lz分别为矩形腔体的长、宽、高；C为常数（下同），此时二面角φ（r）＝π／2

2）球形腔体模数

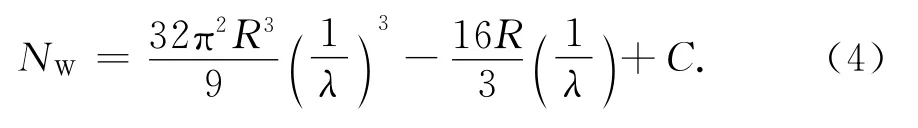
式中：R为球形腔体半径，此时平均曲率ρ（r）＝R，二面角φ（r）＝π.3）圆柱腔体模数

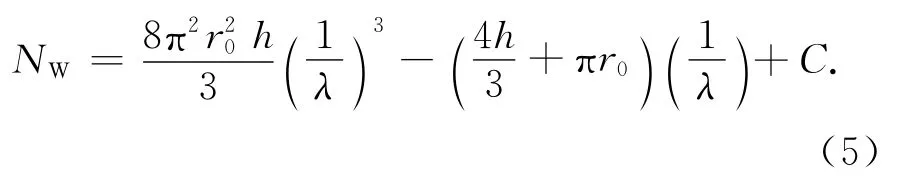
式中：r0为圆柱腔体半径；h为高.

通过对比分析上述各形状腔体的模式模型得到：当本征频率足够高时，即Vλ≫1时，等式（1）右边的第二部分与第一部分的比将趋于零，即

该结果表明：电大尺寸特征下，腔体几何结构对模数的影响可忽略不计.而复杂腔体内本征频率的统计分布特征却与腔体的几何结构相关.为此，在上述模式模型的基础上，基于本征模间隔，进一步分析腔体的混沌特性.

1.2 本征模间隔分析

若忽略本征频率的简并作用，则在本征频率fi处累积模数N（fi）可表示为［12］

式中，符号＃表示对所有符合集合条件枚举的数量.现实中累积模数往往是不平滑的，通常将累积模数N（f）分解为平滑部分NW（fi）和浮动部分Nf（fi）两部分，即

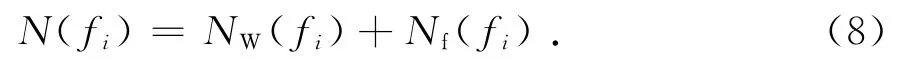
针对浮动部分对系统的影响，可由数值方差Δ2（L）的形式进行分析［13］.若系统为可积系统，则包含L个本征模的数值方差为Δ2（L）＝L；若系统为混沌，则包含L个本征模的数值方差为

方差结果如图1所示.从图中可得到：在给定带宽范围内，可积系统模数的方差与该带宽内模数成正比，斜率k＝1.模数提高，方差增大，系统模数的不确定因素增加.然而混沌系统刚好相反，在高频条件下，斜率趋于0，即

在这种条件下，伴随着模数的增加，混沌系统模数的方差趋于恒定值，这从另一方面反映了混沌系统模数的不确定性趋于稳定值.

综合分析，采用数值方差的方法可以较好区分可积系统与混沌系统.然而，因为数值方差方法很难描述小概率抖动事件，故不能作为研究混沌场概率的预测工具.

图1 本征模数分布

随机矩阵理论作为一种渐进理论，只要获取足够多的状态，即可精确地预测腔体本征模的统计属性.为此，采用基于随机矩阵理论，以最近相邻本征模间隔sn的统计分布来表征腔体系统的混沌特性，可得到较为精确的预测结果［14］，即

当n足够大时，可由随机矩阵系综来描述概率分布函数［15-16］为

式中，s为归一化最近相临本征模间隔sn的随机变量，其中α＝Γv＋1［1＋1／（v＋1）］.

通过式（12）可得到，仅利用单参量v可得到系统本征模间隔的分布特征，如：

1）当v＝0时，系统普适性可由泊松系综来描述，对应的本征模间隔分布可简化为

该分布一般用来描述可积系统，该分布又称为泊松分布.

2）当v＝1时，系统普适性可由高斯正交系综来描述，对应的本征模间隔分布可简化为

该分布一般用来描述不可积系统，对应的分布又称为Wigner分布.

两者的归一化最近相邻本征模数分布规律如图1所示.由图中可以得到：可积系统本征模间隔归一化分布为指数分布，“0”间隔的本征值分布概率最大，这反映了可积系统的大部分本征模“簇拥”一处，近似相等，这就说明可积系统内场的自由度很低；而混沌系统的本征值间隔大部分分布在“1”附近，在两倍间隔之后迅速下降，这反映了混沌系统的大部分本征模在频率轴上是以均匀间隔展开的，从而说明了混沌系统内场具有较高的自由度.

现实中腔体往往介于理想规则腔体和理想混沌之间，即v∈（0，1），随其值增加，归一化间隔分布如图2所示.从图中可以看出，分布的波峰随着参量v的变化而变化.当参量v越靠近0时，对应的概率分布曲线就越接近指数分布；随着参量v增加，波峰逐渐向右移动，其吻合度越接近于Wigner分布；当参量v越靠近1时，对应的概率分布曲线就越接近于Wigner分布.因此，若将参量v作为腔体的混沌性考核指标，通过分析复杂腔体内的混沌性，可总结出一般的规律，这为混沌腔体的设计提供了一定的理论指导.将称v参量为混沌度.

图2 归一化间隔模数分布

2 实验结果分析

为了研究腔体的混沌特性，将按照单规则腔体到多布尔组合体的思路，结合数值试验技术和最小二乘曲线拟合方法，对腔体的混沌特性展开试验研究.

2.1 试验方案设计

考虑工程的可实现性问题，以某铝制矩形混响腔体（7.3m×4.77m×3.25m）为主要研究对象（腔体侧壁电导率为3.8e7s／m，相对介电常数为1，相对磁导率为1.000 021，腔内媒质为空气），将不同尺寸的球形腔体嵌于矩形腔体的顶角处，方案如下：

1）设定球形半径的步进为0.1m，对不同半径的球形腔体本征模分布特征进行分析，得到不同半径球形腔体的混沌度；

图3 Sinna（左）、Stadium（右）腔体

2）将步骤1）中不同半径的球形腔体嵌于矩形腔体的各个顶点处，并进行布尔减运算，得到Sinna腔体（如图3（a））.依据球心放置位置的不同，划分为4种不同的组合：①球形腔体的球心在矩形腔体的H顶角处为Sinna-1腔体；②球心在A、H顶点的Sinna-2腔体；③球心在A、D、F、G顶点的Sinna-4腔体；④球心在八个顶点的Sinna-8腔体；

3）依次类推，将球形腔体与矩形腔体进行布尔和运算，得到的腔体结构如图3（b），该类腔体称为Stadium腔体，按照步骤2）的命名方法，对应4类腔体：Stadium-1、Stadium-2、Stadium-3、Stadium-4；

4）根据矩形腔体及球形腔体结构的相对位置不同，设定组合腔体Sinna-1、Sinna-2、Stadium-1、Stadium-2中的球半径为0.1～3.0m，组合Sinna-4、Sinna-8、Stadium-4、Stadium-8中的球半径为0.1～1.6m.

利用HFSS软件中的本征模求解器，对上述各状态下腔体的前201个本征频率进行求解，将所得的本征频率带入上述对应的本征模数公式（1）得到各个本征频率状态下腔体的本征模数，并依据式（11）对201个本征模数进行归一化模数间隔处理得到（s1，s2，…，s200），利用Matlab软件对归一化本征模数间隔进行分析，并采用最小二乘法对式（12）进行非线性曲线拟合，得到各个状态下混沌特性.

2.2 混沌特性分析

图4 矩形腔体归一化本征模累积概率分布

通过对矩形腔体、球形腔体的归一化本征模间隔进行试验分析，结果（如图4）表明这两类腔体的混沌特性与尺寸没有太大的直接关系.对累积概率密度进行最小二乘曲线拟合后得到矩形腔体的混沌度v≈0.15，这说明了该类腔体属于低混沌度腔体，本征模数的归一化间隔分布趋于指数分布（泊松分布），因此可利用泊松正交系综来描述这类系统的普适性.同理，对不同半径的球体进行混沌度分析，得到混沌度随半径变化的分布曲线如图5.通过分析得到：球形半径在1.1≤r≤3.0m范围内，混沌度分布在0.0～0.1、0.1～0.2、0.2～0.3之间的概率分别为35%、45%、20%，由此说明球体混沌度大部分落在0.1～0.2之间，基本不随球半径的变化而变化，显然这类球体亦属于低混沌度的可积系统.然而当多个矩形、球形等可积系统组合一起，系统混沌特性将不仅仅是它们之间的线性叠加，而变得更加复杂，通过仿真试验分析得到Sinna腔体、Stadium腔体的混沌度随着球半径变化的分布曲线如图6.通过对比分析得到：Sinna-1、Sinna-2腔体的球半径在1.4m以上时，混沌度高于0.9的均占该段总数的13%.在同等条件下，Stadium-1腔体几乎不可能实现，而仅以少量出现在0.7～0.8之间，总体上Sinna腔体比Stadium腔体更容易达到高混沌状态.

图5 球形腔体在不同半径下的混沌特性

图6 Sinna／Stadium混沌度随着球半径变化的分布曲线

通过对比图5、6中的混沌度曲线，总结如下：

1）球形腔体的模数混沌度以v＝0领域内浮动，且大部分集中在［-2，2］，其均值为v＝-0.04，属于低混沌腔体，说明了球形腔体的归一化本征模数间隔分布基本不受球形半径影响，可用泊松系综描述系统的特性；

2）总体上，Sinna腔体较之Stadium腔体有较强的混沌特性，其中表现最为明显的是8类腔体，其次是1类和2类，最后是4类腔体；

3）在总结步骤2）的基础上，可进一步得到，内凹腔体比外凸腔体，具有更明显的混沌特性.

3 结 论

基于量子理论对矩形、球形等常见规则腔体的混沌特性进行分析，结果表明这些规则腔体的混沌特性不受尺寸的影响，混沌度基本较低，从而说明它们的可积性，因此可通过泊松系综矩阵来分析本征模的分布规律.在此基础上，对常规腔体及其布尔组合进行仿真分析，结果表明相同的球形半径下Sinna腔体较Stadium腔体具有较强的混沌特性，从另一方面说明了具有内凹结构特征的腔体比外凸的具有更高的混沌特性，这为以后复杂腔体的混沌特性研究奠定了理论基础，同时也为混响室设计、试验提供了一定的理论指导.

［1］谭武端.电磁混响室内场统计特性及结构优化［D］.西安：第二炮兵工程大学，2013.TAN Wuduan.Statistic Characteristic of Field and Structure Optimization for Electromagnetic Reverberation Chamber［D］.Xi’an：The Second Artillery Engineering University，2013.（in Chinese）

［2］DÖRR U，STÖCKMANN H J.Scarred and chaotic field distributions in a three-dimensional sinai-microwave resonator［J］.Physical Review Letters，1998，80（5）：1030-1033.

［3］STÖCKMANN H J.Microwave studies of chaotic billiards and disordered systems［J］.Journal of Modern Optics，2002，49（12）：2045-2059.

［4］谭武端，余志勇，宋建社，等.混响室的混沌特性及其场统计分布［J］.强激光与粒子束，2013，25（4）：940-944.TAN Wuduan，YU Zhiyong，SONG Jianshe，et al.Chaotic characteristics and statistic distribution of field in reverberation chamber［J］.High Power Laser and Particle Beams，2013，25（4）：940-944.（in Chinese）

［5］COZZA A.The role of losses in the definition of the overmoded condition for reverberation chambers and their statistics［J］.IEEE Transactions on Electromagnetic Compatibility，2011，53（2）：209-307.

［6］MONSEF F，COZZA A.Average number of significant modes excited in a mode-stirred reverberation chamber［J］.IEEE Transactions on Electromagnetic Compatibility，2014，56（2）：259-265.

［7］庄信武，余志勇，刘光斌，等.混沌腔体的统计电磁预测技术［J］.强激光与粒子束，2014，26（3）：197-203.ZHUANG Xinwu，YU Zhiyong，LIU Guangbin，et al.Electromagnetic statistical prediction of chaotic cavities［J］.High Power Laser and Particle Beams，2014，26（3）：197-203.（in Chinese）

［8］庄信武，余志勇，刘光斌，等.基于广义极值的混沌电场峰值分布研究［J］.强激光与粒子束，2014，26（7）：174-179.ZHUANG Xinwu，YU Zhiyong，LIU Guangbin，et al.Analysis of chaotic electric maximum field by generalized extreme value［J］.High Power Laser and Particle Beams，2014，26（7）：174-179.（in Chinese）

［9］唐亚平，徐大专，朱秋明，等.复杂城市环境三维高斯波束跟踪预测模型［J］.电波科学学报，2014，29（1）：86-91＋121.TANG Yaping，XU Dazhuan，ZHU Qiuming，et al.A new 3DGaussian beams launching and predicting model in complex metropolis environment［J］.Chinese Journal of Radio Science，2014，29（1）：86-91＋121.（in Chinese）.

［10］陆希成.复杂腔体电磁耦合效应的统计方法研究［D］.西安：西北核技术研究所，2010.LU Xicheng.Statistical Method Study in Electromagnetic Coupling of Complex Cavities［D］.Xi’an：Northwest Institute of Nuclear Technology，2010.

［11］ORJUBIN G，RICHALOT E，PICON O，et al.Chaoticity of a reverberation chamber assessed from the analysis of modal distributions obtained by FEM［J］.IEEE Transactions on Electromagnetic Compatibility，2007，49（4）：762-771.

［12］COZZA A.Probability distributions of local modaldensity fluctuations in an electromagnetic cavity［J］.IEEE Transactions on Electromagnetic Compatibility，2012，54（5）：954-967.

［13］MEHTA M L.Random Matrices［M］.Salt Lake City：Academic Press，2004.

［14］COZZA A.Probability distributions of local modaldensity fluctuations in an electromagnetic cavity［J］.IEEE Transactions on Electromagnetic Compatibility，2012，54（5）：954-967.

［15］DEUS S，KOCH P M，SIRKO L.Statistical properties of the eigenfrequency distribution of three-dimensional microwave cavities［J］.Physical Review E，1995，52（1）：1146.

［16］STÖCKMANN H J，CHAOS Q.An Introduction［M］.Cambridge：Cambridge Univ Press，1999.