西沙海域天然气水合物地震资料高密度双谱速度分析技术探讨*
2015-03-08陈宏文张宝金
邢 涛 陈宏文 张宝金
(国土资源部海底矿产资源重点实验室 广州海洋地质调查局 广州 510075)
发展海洋天然气水合物的地球物理探测高新技术, 包括数据采集、高分辨率成像为主的处理系统与地质、地球物理和地球化学综合解释技术, 是准确了解天然气水合物的分布与蕴藏量的关键(马在田等,2000)。在天然气水合物地震资料研究中, 速度反转、地震剖面上的似海底反射层 BSR强反射界面之上的高速异常带是水合物的典型表现特征, 速度异常是水合物地层最重要的识别标志之一(宋海斌等, 2002,2003)。速度分析是资料处理的关键环节, 对整个处理质量有决定性作用, 也是速度异常研究的基础条件,高精度速度分析有助于寻找水合物矿点、判定水合物层位(梁劲等, 2006)。同时高质量的地震波速度也可作为AVO分析、无井约束反演等研究的重要参数(张宝金等, 2008)。因此, 高质量的速度分析是水合物地震资料处理中的重要内容。
常规的速度分析技术是基于各向同性假设, 基于双曲线方程计算走时的, 没有考虑到地层真实的各向异性的影响。近些年来随着海上地震采集技术的不断发展, 电缆长度不断增加, 使得地层各向异性的影响更加突出, 其结果严重影响了地震数据的成像质量(庄祖垠等, 2013)。高密度双谱速度分析是双曲线动校正的基础上综合考虑各向异性, 使远偏移距的道集得到很好的校正, 并逐点地进行速度分析来得到空间上细致的速度分布状态, 采用速度自动拾取的方法来避免人为拾取带来的误差, 从而达到高质量速度分析的目的。
1 理论与原理
常规的速度分析基于各向同性假设、双曲近似计算走时。在偏移距和目的层深度比值较小的时候,多层介质的速度值可以用均方根速度代替, 这种假设误差较小。在水平层状各向同性介质中, 在小偏移距近似的情况下, Dix双曲线方程如下
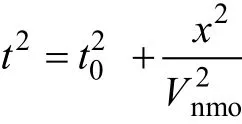
当偏移距和目的层深度比值较大而引起的误差增大的时候, 需要在常规速度分析的基础上综合考虑远偏移距的各向异性问题(Alkhalifah,2000)。
Thomsen将各向异性问题的影响从各项同性背景中分离出来, 提出了各向异性参数和线性近似公式(Thomsen, 1986; Tsvankin, 1996), 更直观地表征了各向异性的物理意义, 说明了各向异性在资料处理中的重要性(Helbig et al, 2005)。Tsvankin提出了适用于各向异性介质和长偏移距的非双曲线 NMO 方程(Tsvankin et al, 1994, 1995)。Alkhalifah和Tsvankin提出了有别于常规单参数速度分析的双参数 Vnmo和 η的速度分析方法(Alkhalifah et al, 1995, 1997), 来进行非双曲时差速度校正, 在任意各向异性情况下的非双曲线时差方程如下

式中: Vnmo为NMO速度, η为各向异性参数。从公式可以看出, 各向异性参数在远偏移距时更明显地改变了反射波走时的计算(徐翠娥等, 2008)。
Siliqi经过深入研究提出: 在垂直各向异性介质中, 将双曲线方程变换成用V和其他参数表示的非双曲线方程(Siliqi et al, 2000 ; Siliqi, 2001), 如下式
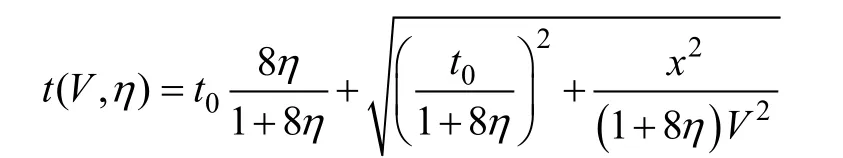
式中: V为NMO速度, η为各向异性参数(非椭圆率), x为偏移距, t0为零偏移距走时。当η等于0或者当偏移距深度比值很小时, 方程收敛为经典的双曲线动校正方程。由此可见各向异性参数 η对时差计算的影响是不规则分布的, 主要集中在远偏移距。在应用于实际资料计算时, 必须将速度V和各向异性参数η结合起来, 采用双谱分析技术, 才能有效地解决远偏移距下的各向异性问题。
2 高密度双谱速度分析参数拾取
高密度双谱速度分析是在每一道都进行速度分析, 在提高速度分析密度的同时综合考虑各向异性的影响, 是由 Siliqi等(Le Meur et al, 2003;Siliqi et al, 2003)提出的。该方法基于前文所述的理论原理, 根据非双曲线时差方程进行分析, 与常规的速度分析方法相比, 双谱速度分析方法的优点在于同时扫描V和η两个参数(潘成磊等, 2010)。
在分析过程中, 加入两个参数dtn和τ0来进行非双曲线校正。参数dtn为最大偏移距时的剩余时差, τ0为零偏移距走时, 参数示意图如图1所示。
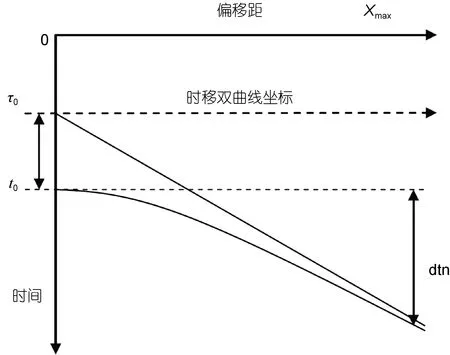
图1 双谱分析参数dtn和τ0示意图Fig. 1 Schematic diagram of dtn and τ0 in bispectral analysis
通过公示变换, 由V-η影响的非双曲线动校方程可以转换为dtn-τ0来表征, 具体公式如下
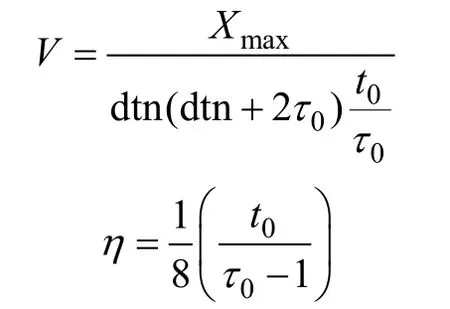
从而 dtn-τ0对可以随时转化为 V-η对, 这样就可以通过扫描 dtn-τ0来转换获得 V-η参数, 从而完成双谱速度分析。
在上述双谱速度分析方法的基础上, 法国 CGG公司研发了相关处理模块来实现高密度双谱速度分析, 具体实现流程如图2所示。
首先对道集数据进行高密度双谱自动速度拾取(hdpic), 扫描并拾取参数 dtn和 τ0后, 分解成对应的低频分量和高频分量; 然后对得到的dtn和τ0的高频分量分别进行地质统计滤波(hdfil), 消除分量中的一些突变和噪音, 使高频分量部分连续性更好, 有利于接下来的处理; 再将处理过的高频分量和之前的低频分量合并(hdbox), 生成新的dtn和τ0; 最后将dtn-τ0转化为速度和各向异性参数 V-η, 应用于道集数据中进行高密度非双曲线动校正, 从而得到解决各向异性问题后的高密度叠加数据体。
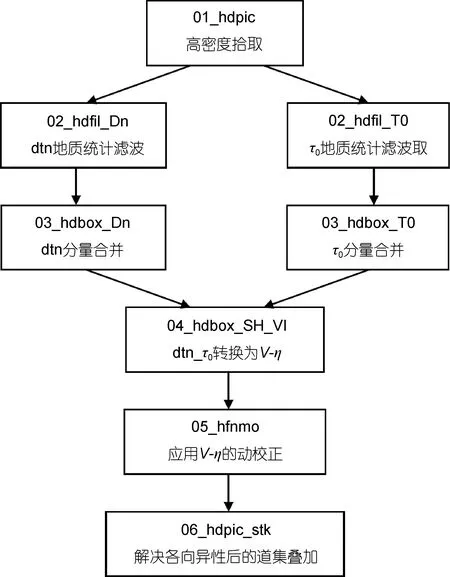
图2 高密度双谱速度分析流程Fig. 2 The flowchart of high-density bispectral velocity analysis
3 天然气水合物地震资料应用效果
采用南海西沙海域天然气水合物二维高分辨率多道地震数据资料, 使用 Geovation地震资料处理系统进行处理。针对典型测线进行保真处理, 经过去多次波、反褶积、高精度速度分析、叠前时间偏移等处理, 得到了较为理想的偏移剖面。之后, 重点对叠前时间偏移数据进行高密度双谱速度分析, 通过高密度双谱非双曲线型NMO自动拾取, 使叠前资料的每一道和每一个采样点都有各向异性速度场, 最终获得解决各向异性问题后的叠前时间偏移剖面。
本次天然气水合物地震二维资料的最大偏移距为3150m。从图3道集对比中可以看出, 在高密度双谱速度分析校正之前的道集上, 同相轴在远偏移距位置, 常规速度分析无法校平, 存在校正过量或者校正不足的现象, 各向异性问题对校正结果影响非常明显。在经过高密度双谱速度分析校正之后, 同时分析拾取速度和各向异性参数, 使得道集在远偏移距位置的同相轴得以拉平, 提高了成像质量。从图4的剖面对比中可以看出, 在高密度双谱速度分析之后,各向异性解决使远偏移距有了更多的有效信息参与到数据处理之中, 使得反射波的同向轴更为连续和清晰, 整体能量也得到了增强, 剖面的细节刻画更加明确, 特别是水合物目标层所在的浅层的信噪比和分辨率有了非常明显的提升。从图5中可以看出, 相对于常规速度分析的速度场, 经过高密度双谱分析之后, 每个 CDP和每个采样点都自动拾取速度形成的速度场在保证速度自动拾取准确性的同时, 提高了分辨能力和分析密度, 更为准确清晰地反映了剖面的地质构造。

图3 高密度双谱速度分析前后动校正道集对比Fig. 3 Contrasts of corrected gathers(a. hyperbola moveout; b. nonhyperbolic moveout)

图4 高密度双谱速度分析前后叠前时间偏移剖面对比Fig. 4 Contrast of PSTM results (a. conventional velocity picking; b. high-density bispectral velocity picking)
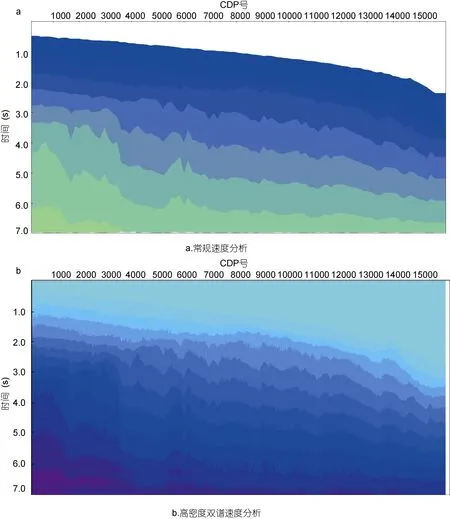
图5 高密度双谱速度分析前后速度场对比Fig. 5 Contrast of Velocity field (a. conventional velocity picking ; b. high density bispectral velocity picking)
综上, 高密度双谱非双曲线动校对远偏移距的同相轴进行了拉平, 从而使得远偏移距有更多的有效信息可以参与叠加, 在每道和每个采样点都获得各向异性速度场的条件下, 明显改善了复杂地质构造区域的成像效果, 提高了叠前偏移剖面的处理质量。
4 结论
(1)高密度双谱速度分析技术采用的是非双曲线动校正, 在常规双曲线动校的基础上综合考虑各向异性的影响。各向异性参数的准确计算, 有效解决了常规速度分析中远偏移距的道集校正不平的问题。
(2)高密度双谱速度分析方法实现了速度逐道逐点的自动拾取, 抛弃了常规速度分析的速度插值方法, 避免人为拾取带来的误差, 使得速度场有着更高的精确度, 提高了时间方向的分辨能力、空间方向的分析密度, 可以充分挖掘水合物地震数据的潜力。
(3)高密度双谱速度分析技术保留了更多的远道信息, 使更多的有效信息参与到数据处理中。处理后反射同向轴更为清晰连续, 剖面细节刻画更加明确, 特别是水合物目标层所在的浅层的信噪比和分辨率有了非常明显的提升, 整体成像质量得到明显提高, 为天然气水合物地震勘探提供了一种更为可靠的技术手段。
(4)高密度双谱速度分析方法对用于分析的数据资料要求较高。由于各向异性参数受近偏移距时差影响, 准确的常规速度分析是研究各向异性的基础条件。此外, 各种噪音引起的信噪比偏低等, 都会对各向异性分析产生干扰。本文在数据准备阶段严格质控,以高质量的叠前时间偏移数据和精细的常规速度分析作为基础, 充分保证了高密度双谱速度分析结果的准确性。
马在田, 宋海斌, 孙建国, 2000. 海洋天然气水合物的地球物理探测高新技术. 地球物理学进展, 15(3): 1—6
庄祖垠, 麻志国, 王志亮等, 2013. 高密度各向异性速度分析技术及应用. 工程地球物理学报, 10(1): 51—56
宋海斌, 江为为, 张文生等, 2002. 天然气水合物的海洋地球物理研究进展. 地球物理学进展, 17(2): 224—229
宋海斌, 张 岭, 江为为等, 2003. 海洋天然气水合物的地球物理研究(III): 似海底反射. 地球物理学进展, 18(2):182—187
张宝金, 张光学, 耿建华等, 2008. 南海含天然气水合物地层速度反演方法探讨. 南海地质研究, (00): 78—85
徐翠娥, 郝晓红, 王 影, 2008. 高密度双谱分析法在各向异性介质速度分析中的初步应用. 海洋石油, 28(1): 1—5
梁 劲, 王宏斌, 郭依群, 2006. 南海北部陆坡天然气水合物的地震速度研究. 现代地质, 20(1): 123—129
潘成磊, 张智勇, 郭廷超, 2010. 高密度速度分析在YA高精度三维的应用. 复杂油气藏, 3(4): 39—42
Alkhalifah T, 1997. Velocity analysis using nonhyperbolic moveout in transversely isotropic media. Geophysics, 62(6):1839—1854
Alkhalifah T, 2000. An acoustic wave equation for anisotropic media. Geophysics, 65(4): 1239—1250
Alkhalifah T, Tsvankin I, 1995. Velocity analysis for transversely isotropic media. Geophysics, 60(5): 1550—1566
Helbig K, Thomsen L, 2005. 75-plus years of anisotropy in exploration and reservoir seismics: a historical review of concepts and methods. Geophysics, 70(6): 9ND—23ND
Le Meur D, Siliqi R, Gamar F et al, 2003. High density moveout parameter fields V and η. Part Two: Simultaneous geostatistical filtering. Dallas, Texas: SEG Technical Program Expanded Abstracts
Siliqi R, 2001. Technological leap in time processing focuses the data throughout anisotropic media. First Break, 19(11):612—618
Siliqi R, Bousquie N, 2000. Anelliptic time processing based on a shifted hyperbola approach. Calgary, Alberta: SEG Expanded Abstracts
Siliqi R, Le Meur D, Gamar F et al, 2003. High-density moveout parameter fields V and η. Part one: Simultaneous automatic picking. Dallas, Texas: SEG Technical Program Expanded Abstracts
Thomsen L, 1986. Weak elastic anisotropy. Geophysics, 51(10):1954—1966
Tsvankin I, 1996. P-wave signatures and notation for transversely isotropic media: an overview. Geophysics, 61(2): 467—483 Tsvankin I, Thomsen L, 1994. Nonhyperbolic reflection moveout in anisotropic media. Geophysics, 59(8): 1290—1304
Tsvankin I, Thomsen L, 1995. Inversion of reflection travel-times for transverse isotropy. Geophysics, 60(4): 1095—1107
