深水波浪破碎与气体交换速率之间的关系*

李竹花 赵栋梁 周桂地

(中国海洋大学海洋环境学院 青岛 266100)

研究海-气界面 CO2通量时, 气体交换速率 k是表征海-气界面气体交换强度的重要参量, 也是实际计算中最难确定的参量。气体交换速率与海面附近的湍动能耗散率密切相关, 但直接观测湍动能耗散率比较困难, 一般通过其他可观测参量对气体交换速率进行参数化, 其中最为常用的是风速参量,Wanninkhof等(2009)对此进行了比较详尽的叙述。然而, 不同作者给出的气体交换速率与风速的关系差异非常大, 给海-气界面 CO2通量的计算带来了很大的不确定性。这表明单一风速参量无法完全描述气体交换速率。有研究指出, 风浪及其破碎直接影响海气界面的气体交换过程(Soloviev et al, 2007; Zappa et al,2007; Tokoro et al, 2008), 因此, 波浪对气体交换的影响应在k的参数化表达式中予以体现。

海洋表面由粘性次层和湍流边界层组成, 气体分子穿越海表面的速度取决于其在两层内的传输速度。粘性次层厚度非常薄, 气体分子在该层内的穿越速率由Schmidt数

决定, 式中νw为水的运动学粘性系数, D则为气体分子在水中的运动学扩散系数。Schmidt数是温度的函数(Wanninkhof, 1992), 是一个容易观测且比较确定的参数。湍流边界层内以湍流运动为主, 通常采用湍动能耗散率ε表征其强度。由于湍流运动强度远强于分子运动, 故而, 跨越海-气界面的气体交换速率主要取决于粘性次层的厚度, 湍动能耗散率越大, 粘性次层越薄, 越有利于海-气界面的气体交换。基于表面更新或小涡理论得到气体交换速率与湍动能耗散率之间具有1/4次方的关系(Danckwerts, 1951; Banerjee et al, 1968; Lamont et al, 1970; Kitaigorodskii, 1984),具体表达式为

式中A为待定系数。粘性次层的厚度δυ可表示为

该厚度又称为 Kolmogorov微尺度, 代表湍流运动的最小尺度。

因此, 如何测量海-气界面下水体的湍动能耗散率成为关键。然而, 湍动能耗散率与气体交换速率的同步观测只是在近年来才实现(Soloviev et al, 2007;Zappa et al, 2007; Tokoro et al, 2008), 大面积、长时间尺度观测的获取依然困难, 在实际应用中仍然存在很大的局限性。

在深水海域中, 波浪破碎造成波浪能量的耗散,为海表面附近的湍流运动提供了主要能量来源, 因此波浪能量耗散率与湍动能耗散率之间应该具有密切的联系。为了获得波浪能量耗散率的值, Hasselmann(1974)和 Phillips(1985)等分别提出谱耗散模型, 利用海浪谱数据计算波浪能量耗散率。然而, 海浪谱并非常规观测量, 在实际应用中必然存在一定的困难。为了解决这个问题, 本文根据谱耗散模型计算所得的波浪能量耗散率与常规观测参量-风速建立关系, 并将湍动能耗散率作为中间变量, 建立气体交换速率与波浪能量耗散率的直接关系式, 探讨利用海浪数值模式计算气体交换速率的可行性。

本文的主要内容如下: 第一节中介绍浮标数据的选取及预处理、浮标观测数据所得波浪能量耗散率及其与风速参量之间的关系。第二节首先建立了波浪能量耗散率与气体交换速率之间的经验关系式, 进而利用浮标数据确定关系式中的未知参量。第三节介绍了由海浪模式得到的波浪能量耗散率和气体交换速率。第四节给出了本文的结论。

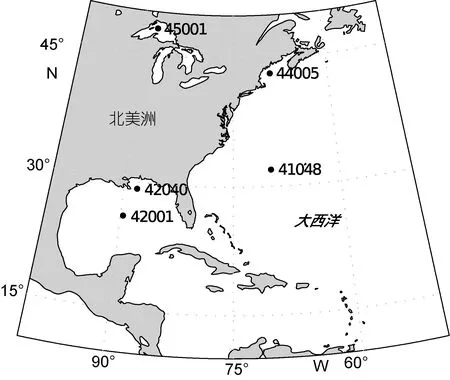
图1 浮标站位的分布Fig.1 Distribution of the buoy stations

1 波浪能量耗散率

1.1 浮标数据及预处理

1.1.1 选取浮标站位 为了避开近海环境的复杂性, 本文主要研究深水风浪的波浪能量耗散率, 即白冠耗散。为此, 选用美国国家数据浮标中心(NDBC)的深水浮标数据, 利用 2007年全年的风速和海浪频谱的观测资料进行计算。

图1所示为选用五个浮标站位的位置, 水深均在200m以上。为避免涌浪的影响, 在选择浮标站位时考虑了以风浪为主的位置。为了保证观测数据涵盖较大的风速范围, 选择了墨西哥湾内的两个深水站位42001和42040站。由于墨西哥湾内经常发生台风, 因而该湾内两站位的选取有利于高风速数据的获得,且容易产生纯风浪。另外, 选用位于大西洋内的41048和44005站, 其中44005站位于大西洋沿岸, 不同方向的风区差异很大, 代表风区较短的情形,41048站远离大西洋沿岸, 风区较大, 代表风区较长的情形。

1.1.2 提取纯风浪数据 风浪频谱一般为单峰,而涌浪频谱往往出现双峰甚至多峰。若低频处存在一个能量较小的峰值, 则属于风浪占优的情形。为了获取纯风浪的频谱数据, 在剔除异常数据后, 首先去掉双峰和多峰的情况, 然后对剩下的数据应用下列判据。

1) 根据Toba(1972)的3/2指数律:

提取满足0.05≤B≤0.074的数据; 其中Hs和Ts分别表示有效波高和有效周期, U10代表10m高度处的风速, g为重力加速度。

2) 选取满足波龄 β=cp/U10≤1.2(Pierson, 1991)的数据, 式中cp为主组成波的相速度。

3) 选取满足Lp/d＜2的数据, 式中d代表水深, Lp为主组成波的波长。

1.1.3 摩擦风速 根据拖曳系数的定义, 可以得到空气摩擦风速与风速之间的关系为其中 Cd称为拖曳系数, 在 U10已知的情况下, 采用Wu(1988)提出的拖曳系数表达式得到摩擦风速的值。

1.2 波浪能量耗散率与风速的关系

Hasselmann(1974)认为尽管波浪破碎属于局地强非线性过程, 平均意义上非线性较弱。最低阶的能量耗散应该是海浪谱的准线性过程, 耗散谱形式为

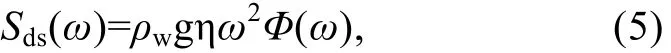
式中ρw=1025kg/m3代表海水的密度, ω为频率, Φ(ω)为海浪频谱, η为常数。Komen 等(1984)给出η的值如下

其中Dht单位是kg/s3。波浪能量耗散率与海浪频谱密度呈线性关系。

Phillips(1985)提出平衡域的概念, 即: 波浪场的高频部分——风浪成分, 与局地风基本处于平衡状态, 是波浪破碎发生的主要区域, 给出的平衡域的频率谱为

式中α为Toba常数。各源项量级相当且对应成比例,因此耗散谱的表达形式为

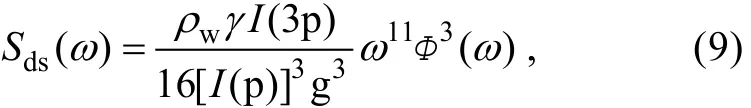
式中I(p)=∫(cosθ)pdθ为表面风浪扩展函数。假定风能输入项与耗散项量级相当, 则 γδ2≈0.04, 其中δ=α/4I(p)。依据 Felizardo 等(1995)(下称 FM95),Phillips模型中两个常量取值为 α=0.11和 p=0.5。因此, 由Phillips模型的波浪能量耗散率为

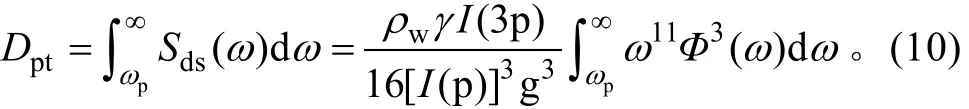
采用式(7)和(10)计算得到的波浪能量耗散率 Dht和Dpt与U10的关系见图2(a, b)。

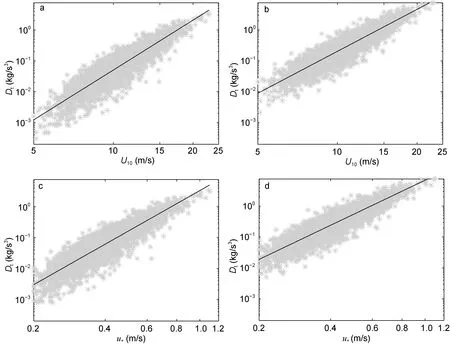
图2 浮标数据计算的Dt与风速U10和u*的关系。灰色散点代表浮标实测数据, 实线为最小二乘拟合结果。a和c代表Hasselmann模型的结果, b和d为Phillips模型的计算结果Fig.2 Relations between Dt and U10 (u*) that are derived using the observational data of the buoy. Gray scatters are the observations and the solid lines represent results of the least-square fitting. The left panel (a and c) represent results of the Hasselmann model, and the right panel (b and d) represent those of the Phillips model

图中显示波浪能量耗散率Dt(即: Dht和Dpt)与U10存在较明显的指数关系, 即

对上述所得的 Dt和 U10的对数值进行最小二乘拟合,得到的系数a和b和相关系数R见表1, 具体表达式如下所得拟合曲线见图2(a, b)中的实线。

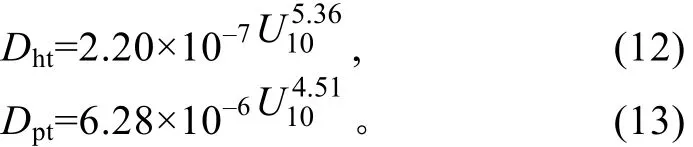
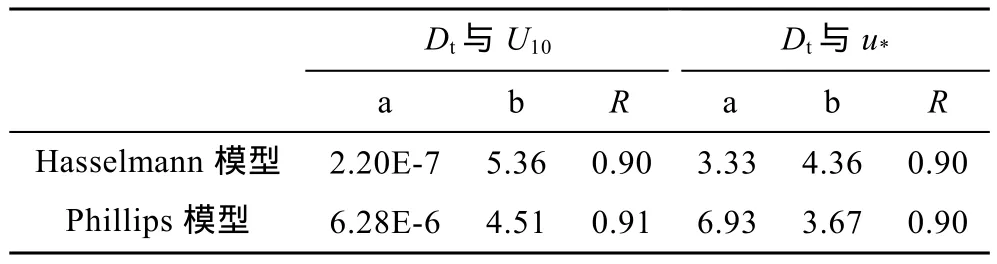
表1 纯风浪浮标数据Dt与风速关系式的参数Tab. 1 Parameters in relations between Dt and wind speed

Hanson等(1999)(下称 HP99)在开阔大洋进行了波浪成长与耗散的观测, 剔除涌浪成分后利用Phillips模型估算波浪能量耗散率。FM95在开阔海域观测了环境噪声谱, 研究其与波浪能量耗散率的关系。该观测海域风区大, 波浪趋于充分成长状态。

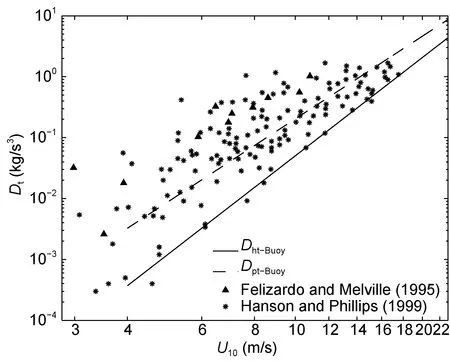
图3 浮标数据计算的Dt与U10的关系与文献结果的对比。星号和三角形分别为Hanson等(1999)和Felizardo等(1995)的观测数据, 实线和虚线分别代表Hasselmann模型和Phillips模型计算结果的拟合曲线Fig.3 Relations between Dt and U10 that are derived using the buoy data. Stars and triangles represent observational results from Hanson et al (1999) and Felizardo et al (1995), respectively.Solid and dashed lines represent the results of the Hasselmann model and the Phillips model, respectively

图 3给出了本文研究结果(拟合曲线)与 HP99和 FM95的实测数据的对比。可见 Phillips模型的拟合曲线与 HP99观测数据符合较好; 而Hasselmann模型的结果则靠近该研究的下限。二者都小于FM95的结果。HP99给出的基于Phillips模型的经验公式为

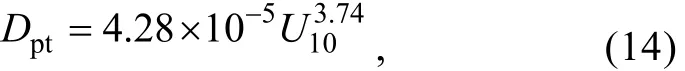
本文给出的结果与之类似, 但系数略小而指数略高。其差别可能是由以下因素引起: 1)所用数据的观测时间、地点和观测长度不同。2)所用风浪提取方法不同。另外, 本文计算的Dpt约是Dht的两倍, 这与FM95的结果一致。

图 2c, d给出了 Dht和 Dpt与摩擦风速 u*的关系,具体表达式如下

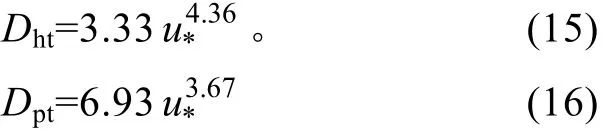
给定平衡域的谱型, Zhao等(2001)利用Hasselmann模型和Phillips模型均给出

可见, 本文给出的指数高于该结果, 与 Phillips模型更为接近。

综上所述, 采用浮标海浪频谱数据, 基于Phillips模型和Hasselmann模型计算的波浪能量耗散率与Zhao等(2001)的结果较为接近。

2 基于浮标数据计算气体交换速率

2.1 气体交换速率与波浪能量耗散率的关系

深水区域发生的波浪能量耗散主要是由波浪破碎造成的, 其耗散的能量是海表面附近湍流的主要能量来源。海洋中的湍流强度可用湍动能耗散率表示,因此, 波浪能量耗散率与湍动能耗散率应具有密切的关系。根据Dpt或Dht的计算公式可以得出, 波浪能量耗散率Dt的量纲为

其中M为质量的量纲, T代表时间的量纲。湍动能耗散率的量纲为

式中L为长度量纲。基于量纲分析, 波浪能量耗散率与湍动能耗散率之间的关系可以写成

式中α为待定常数, z代表湍动能耗散率的计算深度,ρw为海水的密度。上式中z取为粘性次层的厚度δυ(式3)。将上式代入式(2)中, 得到气体交换速率与波浪能量耗散率之间的关系式为

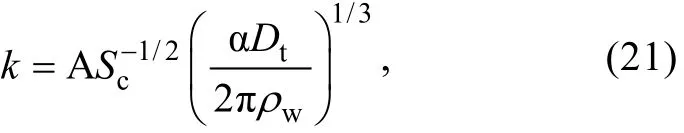
式中的A和α为待定系数。由此建立了k与Dt的关系式, 避免了湍动能耗散率观测的困难。待定常数可利用浮标观测数据确定。

2.2 基于浮标数据计算气体交换速率

根据上述分析, 将 Dpt应用于(21)式计算气体交换速率 k, 并采用最小二乘的方法确定其中的系数Aα1/3。图4给出k与U10的关系及其与文献结果的对比。选取的文献结果(表2)观测区域包含大洋、近海、湖泊、河口和河流以及实验室。图中的一族黑色平行虚线是根据 Zhao等(2010)给出的与波龄β有关的 k与U10的关系式

表2 图4中图例符号对应的参考文献Tab. 2 The references codes used in Fig. 4

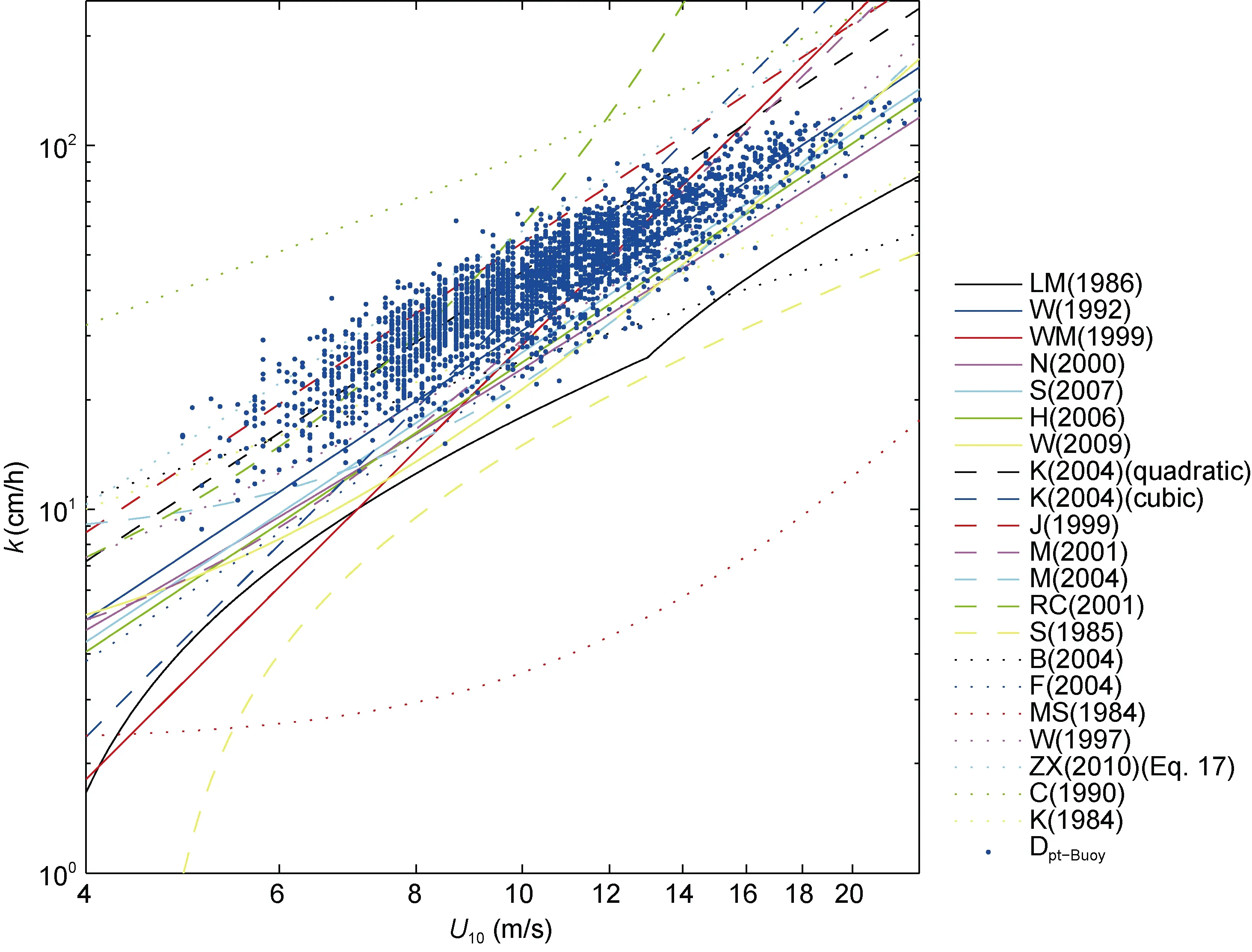
图4 浮标数据计算的气体交换速率k与U10的关系及其与文献结果的比较。散点为浮标计算结果, 曲线为文献结果, 黑色平行虚线为根据(22)式取不同波龄对应的曲线Fig.4 Relation between k and U10 derived by the buoy data and its comparison with results in the literatures. Scatters represent results of the buoy data and curves represent results from literatures. Black parallel dashed lines are obtained using Eq. (22) given different values of wave age

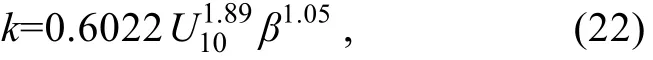
分别令β取不同的值而得到的, 自下向上分别对应于β=0.1 到 β=1.2, 间隔为 0.1。

由图 4可以看到, 文献结果基本处于 β=0.4和β=1.2之间, 选取这两个波龄对应的结果作为气体交换速率的上下限, 利用最小二乘法确定(21)式中的参数 Aα1/3, 其值分别为 0.1384和 0.0425, 取其平均值Aα1/3=0.0905作为Aα1/3的估计值。给出波浪能量耗散率与气体交换速率的关系为

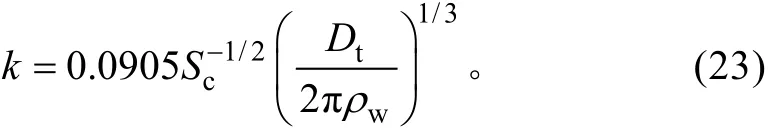
3 基于数值模式计算气体交换速率

3.1 模式设置

海浪数值模拟已成为海浪科学研究中的重要手段, 可以为海浪研究提供大面积、同步的波浪数据。我们分别采用第三代海浪模式中 WAVEWATCHIII(Tolman, 2009)(以下简称 WWATCH)和 SWAN(The SWAN Team, 2010)进行数值计算, 探讨利用海浪数值模式计算气体交换速率的可行性。为了简单又不失代表性, 计算水深取 d=1000m, 计算区域 x方向为4500km, y方向延伸3000km, 网格分辨率为10km。采用4m/s的均匀定常风持续吹拂于研究海域36h, 以消除初始条件的影响; 然后引入随时间线性增强的风速, 72h风速由4m/s逐渐增强到23m/s。由于同一风速持续时间不够长, 计算区域内将产生纯风浪, 且波浪无法达到充分成长状态。

模拟过程中开边界处不采取任何波浪输入, 且在物理过程的选择中, 唯有深水作用被引入计算, 忽略浅水效应。两模式中, 白冠耗散率均采用 Komen等(1984)的公式进行计算。

3.2 模式结果

3.2.1 波浪能量耗散率 图 5给出了模式给出的波浪能量耗散率与风速之间的关系, 及其与浮标结果的对比, 图中所示为海浪模式风区长度为 100—4000km的模拟结果。从图5a可以看到, SWAN模式和 WWATCH模式的模拟结果斜率相差不大, SWAN模式计算的波浪能量耗散率Dst大于 WWATCH的值Dwt, 与FM95的结果接近。中低风速下, WWATCH模式结果与浮标数据的 Phillips模型结果符合较好; 当风速高于14m/s时, 浮标数据逐渐偏离WWATCH的模拟结果, 与SWAN模式的结果接近。模拟结果受风区影响不大。模式所得的Dt与U10的关系式为

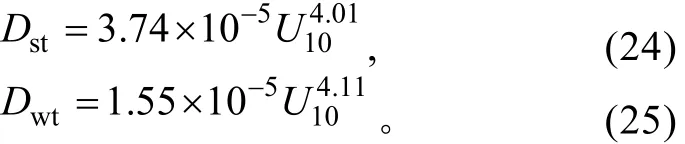
与(3)和(4)式相比, 模式结果的指数偏小, 但与 HP99观测结果接近。图 5(b)给出的 Dt与 u*的关系表达式为

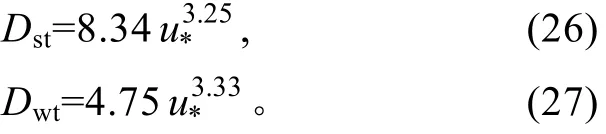
可以看出, 模式结果的指数与Zhao等(2001)所给的更为接近。与SWAN模式相比, WWATCH模式结果接近浮标结果, 更适合应用于气体交换速率的计算。

3.2.2 气体交换速率 采用WWATCH模式计算波浪能量耗散率, 以及基于浮标数据提出的波浪能量耗散率与气体交换速率的关系式(23), 得到的气体交换速率k与风速的关系如图6。

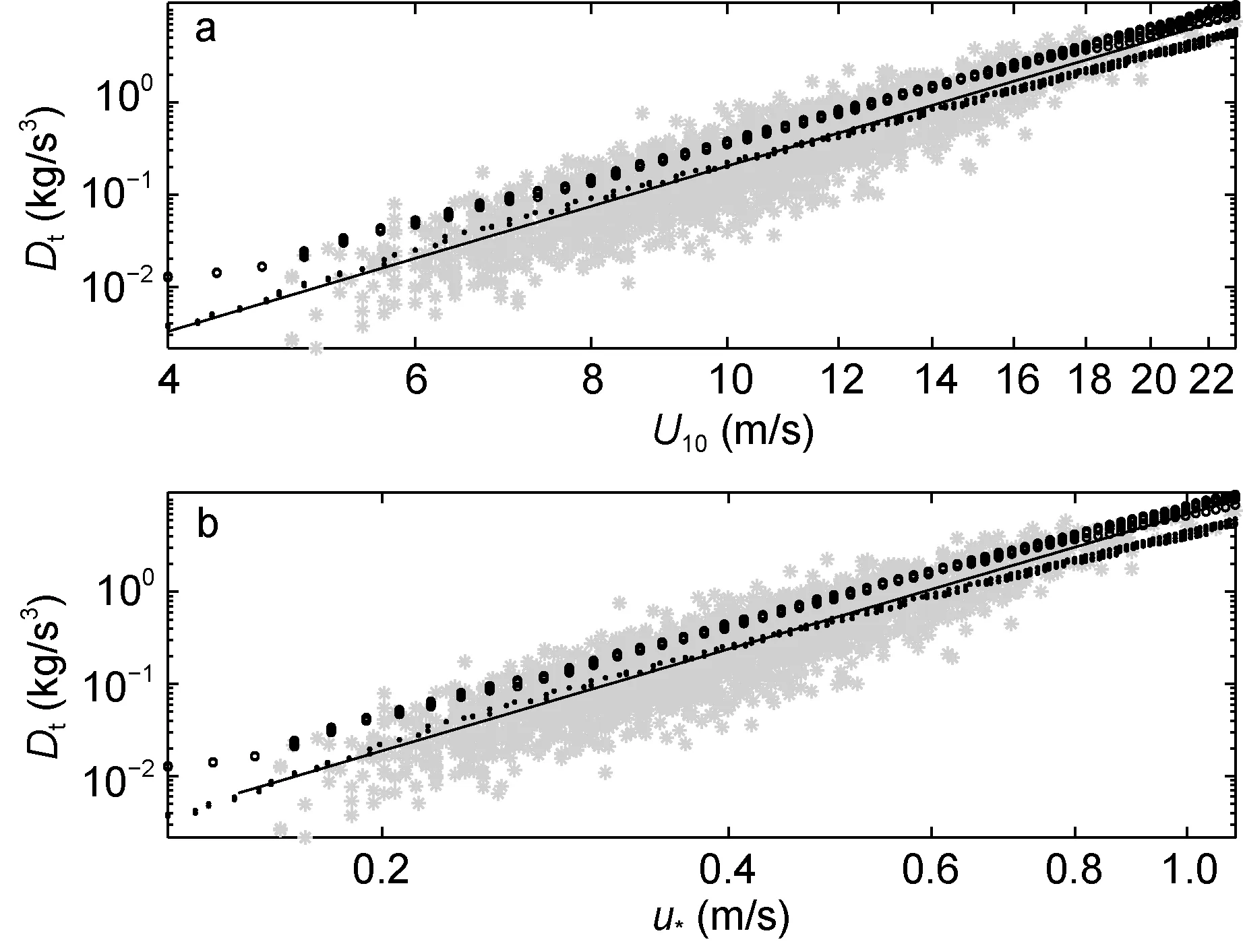
图5 模式计算的Dt与风速U10和u*的关系。灰色散点和实线分别代表浮标实测数据及其最小二乘拟合值, 其Dt均采用Phillips模型进行计算; 圆圈和圆点分别代表SWAN模式和WWATCH模式的模拟值Fig.5 Relations between Dt and U10(u*) that are derived by the model simulations. Gray scatters and the solid lines represent observations of the buoy data and their corresponding results of the least-squares fitting, in which Dpt are used. Black circles and dots represent results obtained using the SWAN model and the WWATCH model, respectively

从图 6可以看出, 在较低风速的情况下, 由WWATCH模式得到的气体交换速率值与现有结果相比偏大; 随着风速的增大, WWATCH模式结果逐渐靠近现有结果。

4 结论

基于浮标观测数据, 本文给出波浪能量耗散率与湍动能耗散率之间的经验关系, 利用 k与 ε1/4的关系, 得到由波浪能量耗散率计算气体交换速率的关系式。利用深水浮标观测数据, 采用Hasselmann模型和 Phillips模型计算了波浪能量耗散率, 建立了其与风速的关系。Phillips模型的计算结果比Hasselmann模型更接近 Zhao等(2001)的结果。基于 SWAN和WWATCH海浪模式计算了波浪能量耗散率,WWATCH模式模拟结果优于SWAN模式, 更适合进行气体交换速率的计算。

图6 WWATCH数值模式所得气体交换速率与文献结果的对比Fig.6 Comparisons between results of the WWATCH model and those in the literatures

Banerjee S, Scott D S, Rhodes E, 1968. Mass transfer to falling wavy liquid films in turbulent flow. Ind Eng Chem Fundam,7(1): 22—27

Borges A V, Delille B, Schiettecatte L et al, 2004. Gas transfer velocities of CO2in three European estuaries (Randers Fjord,Scheldt, and Thames). Limnol Ocean, 49(5): 1630—1641

Csanady G T, 1990. The role of breaking wavelets in air-sea gas transfer. J Geophys Res, 95(C1): 749—759

Danckwerts P V, 1951. Significance of liquid-film coefficients in gas absorption. Ind Eng Chem, 43(6): 1460—1467

Felizardo F C, Melville W K, 1995. Correlations between ambient noise and the ocean surface wave field. J Phys Oceanogr, 25(4): 513—532

Frew N M, Bock E J, Schimpf U et al, 2004. Air-sea gas transfer:Its dependence on wind stress, small-scale roughness, and surface films. J Geophys Res, 109(C8): C08S17, http://dx.doi.org/10.1029/2003JC002131

Hanson J L, Phillips O M, 1999. Wind sea growth and dissipation in the open ocean. J Phys Oceanogr, 29(8): 1633—1648

Hasselmann K, 1974. On the spectral dissipation of ocean waves due to white capping. Bound-Layer Meteor, 6(1—2):107—127

Ho D T, Law C S, Smith M J et al, 2006. Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: Implications for global parameterizations. Geophys Res Lett, 33(16): L16611, http://dx.doi.org/10.1029/2006 GL026817c

Jacobs C M J, Kohsiek W, Oost W A, 1999. Air-sea fluxes and transfer velocity of CO2over the North Sea: Results from ASGAMAGE. Tellus, 51(3): 629—641

Kitaigorodskii S A, 1984. On the fluid dynamical theory of turbulent gas transfer across an air-sea interface in the presence of breaking wind-waves. J Phys Oceanogr, 14(5):960—972

Komen G J, Hasselmann S, Hasselmann K, 1984. On the existence of a fully developed wind-sea spectrum. J Phys Oceanogr, 14(8): 1271—1285

Kuss J, Nagel K, Schneider B, 2004. Evidence from the Baltic Sea for an enhanced CO2air-sea transfer velocity. Tellus,56(2): 175—182

Lamont J C, Scott D S, 1970. An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J, 16(4):513—519

Liss P S, Merlivat L, 1986. Air-sea gas exchange rates:Introduction and synthesis. In: Buart-Ménard P ed. The Role of Air-Sea Exchange in Geochemical Cycling. Norwell, MA,USA: D. Reidel Pub. Co., Sold and distributed in the U.S.A.and Canada by Kluwer Academic Publishers, 113—127

McGillis W R, Edson J B, Hare J E et al, 2001. Direct covariance air-sea CO2fluxes. J Geophys Res, 106(C6): 16729—16745 McGillis W R, Edson J B, Zappa C J et al, 2004. Air-sea CO2exchange in the equatorial Pacific. J Geophys Res, 109(C8):C08S02, http://dx.doi.org/10.1029/2003JC002256

Monahan E C, Spillane M C, 1984. The role of oceanic whitecaps in air-sea gas exchange. In: Brutsaert GHJW ed. Gas Transfer at Water Surfaces. Norwell, MA, USA: D. Reidel Pub. Co., Sold and distributed in the U.S.A. and Canada by Kluwer Academic Publishers, 495—503

Nightingale P D, Malin G, Law C S et al, 2000. In situ evaluation of air-sea gas exchange parameterizations using novel conservative and volatile tracers. Glob Biogeochem Cycles,14(1): 373—387

Phillips O M, 1985. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J Fluid Mech, 156: 505—531

Pierson W J Jr, 1991. Comment on “Effects of sea maturity on satellite altimeter measurements” by Roman E. Glazman and Stuart H. Pilorz. J Geophys Res, 96(C3): 4973—4977

Raymond P A, Cole J J, 2001. Gas exchange in rivers and estuaries: Choosing a gas transfer velocity. Estuaries, 24(2):312—317

Smethie W M Jr, Takahashi T, Chipman D W et al, 1985. Gas exchange and CO2flux in the Tropical Atlantic Ocean determined from222Rn and pCO2measurements. J Geophys Res, 90(C4): 7005—7022

Soloviev A, Donelan M, Graber H et al, 2007. An approach to estimation of near-surface turbulence and CO2transfer velocity from remote sensing data. J Mar Syst, 66(1—4): 182—194

Sweeney C, Gloor E, Jacobson A R et al, 2007. Constraining global air-sea gas exchange for CO2with recent bomb14C measurements. Glob Biogeochem Cycles, 21(2): GB2015,http://dx.doi.org/10.1029/2006GB002784

The SWAN Team, 2010. SWAN scientific and technical documentation for SWAN Cycle III version 40.81

Toba Y, 1972. Local balance in the air-sea boundary processes. J Oceanogr Soc Japan, 28(3): 109—121

Tokoro T, Kayanne H, Watanabe A et al, 2008. High gas-transfer velocity in coastal regions with high energy-dissipation rates.J Geophys Res, 113(C11): C11006, http://dx.doi.org/10.1029/2007JC004528

Tolman H L, 2009. User manual and system documentation of WAVEWATCH III version 3.14

Wanninkhof R, 1992. Relationship between wind speed and gas exchange over the ocean. J Geophys Res, 97(C5):7373—7382

Wanninkhof R, McGillis W R, 1999. A cubic relationship between air-sea CO2exchange and wind speed. Geophys Res Lett, 26(13): 1889—1892

Wanninkhof R, Asher W E, Ho D T et al, 2009. Advances in quantifying air-sea gas exchange and environmental forcing.Annu Rev Mar Sci, 1: 213—244

Woolf D K, 1997. Bubbles and their role in gas exchange. Liss P S, Duce R A eds. The Sea Surface and Global Change.Cambridge: Cambridge University Press, 173—205

Wu J, 1988. Wind-stress coefficients at light winds. J Atmos Oceanic Tech, 5: 885—888

Zappa C J, McGillis W R, Raymond P A et al, 2007.Environmental turbulent mixing controls on air-water gas exchange in marine and aquatic systems. Geophys Res Lett,34(10): L10601, http://dx.doi.org/10.1029/2006GL028790

Zhao D L, Toba Y, 2001. Dependence of whitecap coverage on wind and wind-wave properties. J Ocean, 57(5): 603—616

Zhao D L, Xie L, 2010. A practical bi-parameter formula of gas transfer velocity depending on wave states. J Ocean, 66(5):663—671