探地雷达根系数据的PSO-SA-OMP压缩重构方法1)
2015-03-08李超苏耀文涂文俊张怡卓
李超 苏耀文 涂文俊 张怡卓
(东北林业大学,哈尔滨,150040)
责任编辑:戴芳天。
根系在陆地生态系统能量转换和物质循环中扮演重要角色,不仅具有固定植株、吸收水分和矿物质的功能,而且对于生态系统的碳循环也是至关重要的[1]。因此,研究植物根系的相关参数,如根径大小、分布范围及生物量,对生态系统循环具有重要意义。探地雷达(GPR)作为一种非侵入性探测方法,在根系探测领域正不断改进与完善[2]。Raz-Yaseef N[3]等阐述了探地雷达方法在单株植物根径大小和生物量的估测上具有实效性。郭立[4]等提出了粗根探地雷达信号正演模拟方法,分析了粗根探测精度的敏感因素,改进了探地雷达反演粗根生物量方法,建立了基于探地雷达的根系三维结构模型。
由于探地雷达对根系进行高密度探测时,资源有限,而且采样数据量大,无法实现实时压缩,给传输信道造成巨大压力[5]。屈乐乐[6]等提出了压缩感知框架下的探地雷达技术,对可压缩信号进行稀疏分解、观测测量和重构,有效减少了采集设备的压力。正交匹配追踪算法(OMP)是常用的压缩感知重构算法,但是,OMP 算法每一步分解都要在高维空间进行大量内积计算,所需计算量巨大[7]。杨愚[8]等提出了基于粒子群算法(PSO)优化的OMP重构算法,通过粒子群快速搜索的特点,寻取最佳匹配原子,完成信号重构。针对PSO 容易陷入局部最优解,张建军[9]等提出了基于混合粒子群的匹配追踪算法,但是求出能逼近Hessian 矩阵的正定矩阵较为困难。赵知劲[10]等提出了量子粒子群的运动模式,该算法比基本粒子群算法速度快且精度高,但是由于粒子的中心位置参数设置为区间[0,1]的随机数,造成粒子位置的随机性,导致了算法的不稳定。
模拟退火(SA)是全局寻优算法,能以一定概率接受次优解,能克服PSO 算法陷入局部最优的缺陷[11]。于海平[12]等证明了PSO-SA 算法在多峰信号的应用中,能有效增强PSO 算法的全局搜索能力和稳定性。笔者提出PSO-SA-OMP 的优化方法,针对探地雷达根系数据的快速重构问题,通过PSO算法快速搜索,降低OMP 重构算法运算时间;通过SA 算法,确定全局最优解,提高重构精度。
1 压缩感知框架下的根系数据重构
设m 为探地雷达时间采样点数,n 为探地雷达采样位置点,则可以表示成维度为m×n 的探地雷达数据,用N 维向量x(N=m×n)表示,x=[X1,1,X2,1,…,X1,2,X2,2,…,Xm,n],其在某正交基组成的Ψ 域内可表示为:

式中:Ψ=[Ψ1,Ψ2,Ψ3,…,ΨN],N×1 的列向量s 是投影系数序列,如果s 中仅有K(K≪N)个非零的大系数,则认为x 在Ψ 域内是K 稀疏的。
用M×N 的测量矩阵Φ(M≪N)对x 进行观测得到M 维的压缩向量y:

Gabor 过完备原子库在信号稀疏表示上具有灵活性,能更加准确地表示稀疏信号,因此,采用Gabor 原子构建过完备原子库Θ。一个Gabor 原子由一个经过调制的高斯窗函数组成,如式(3)所示。
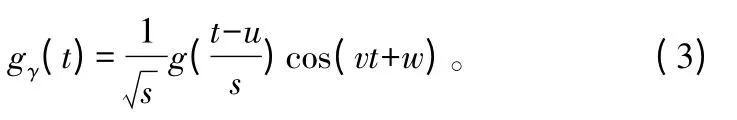
式中:g(t)=e-πt2是高斯窗函数;γ=(s,u,v,w)是时频参数,一个原子由(s,u,v,w)决定;s 是伸缩因子;u 是位移原子;v 是原子的频率;w 是原子相位。时频参数可以按式(4)进行离散化。

式中:a、Δu 为系数参量;Δv、Δw 为相位参量;0<j≤lbN,0≤p≤N2-j+1,0≤k<2j+1,0≤i≤12。
当Θ 满足式(5)所示的约束等距性准则(RIP)时,可通过求解式(6)问题进行恢复。
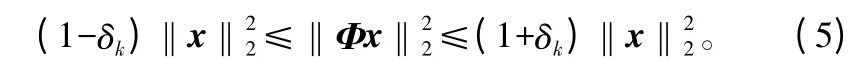
式中:0<δk<1;δk为等容常数。

显然通过求解最小l0范数,从低维信号y 恢复出高维的稀疏信号s 或原始信号x 是NP-hard问题。
OMP 从Θ 中选取构成y 的列向量,重构的关键步骤如下:
①在第p 次迭代中选出最佳原子ip,也就是使信号残差rp-1与列gj相关性最大,即:

②将选中的原子构成集合Hp,采用最小二乘:

③更新残差:

在式(7)中,每一步分解都要在高维空间进行内积计算,造成了其计算时间长。可以选取OMP 的匹配函数|<rp-1,gj>|作为适应度函数,将式(7)看作是求解最优化问题,可以避免大量的内积计算,明显降低重构算法的计算复杂度。
2 PSO-SA-OMP 重构算法
PSO 算法是群体智能算法,源于鸟类捕食行为,算法中每个粒子都代表问题的一个潜在解,粒子在解空间中运动,不断更新粒子的速度和位置,计算适应度值,更新个体极值和群体极值,实现函数求解。SA 算法有加温过程、等温过程和冷却过程,从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性,在解空间中随机寻找目标函数的全局最优解,能量变化就是目标函数,最优解就是能量最低态。
PSO 算法可以快速搜索匹配原子,但是在越来越接近最优解时,粒子速度越来越小,导致粒子群出现“趋同和振荡”现象,使算法不稳定,易陷入局部最小值。而SA 算法能依据Metropolis 准则,以一定概率接受次优解,进行全局寻优,结合两者优点,既减少了OMP 重构过程的运算时间,又保证了重构精度。
在d 维(M×N 维)搜索空间内,Θ 匹配原子搜索优化过程如下:
①初始化参数:种群大小、惯性权重ω、学习因子c1和c2、初始温度T0、迭代次数t 等。给每个粒子在Θ 中生成一随机位置,每个位置对应Θ 中的一个原子。
②第i 个粒子的速度vi=(vi,2vi,2…vi,d)、位置xi=(xi,1xi,2…xi,d),粒子通过不断计算匹配函数的适应度值,选取每个粒子所经历过的具有最好适应度值的位置作为个体最好位置,记为pi(pi1pi,2…pi,d);选取所有粒子所经历过的最好适应度值的位置作为全局最好位置,记为pg(pg,1pg,2…pg,d)。速度和位置更新公式如式(10)、(11)所示。

粒子在解空间范围的速度和位置限制在[-Vmdax,Vmdax]和[-Xmdax,Xmdax]。
③模拟退火算法在退温搜索过程中,在解x 的区域中产生新的可行解x'时,计算f(x')和目标函数f(x)的差值,依照概率min{1,exp(-Δf/Tt)}>rand[0,1]接受解x',其中rand[0,1]表示[0,1]的随机数,因此能够有效避免陷入局部极小值,Metropolis 准则概率公式如式(12)所示。

式中:Tt表示第t 次迭代的温度;Δf 表示计算目标函数f(x')和目标函数f(x)的差值。
根据以上阐述,设计PSO-SA-OMP 算法流程图(见图1)。
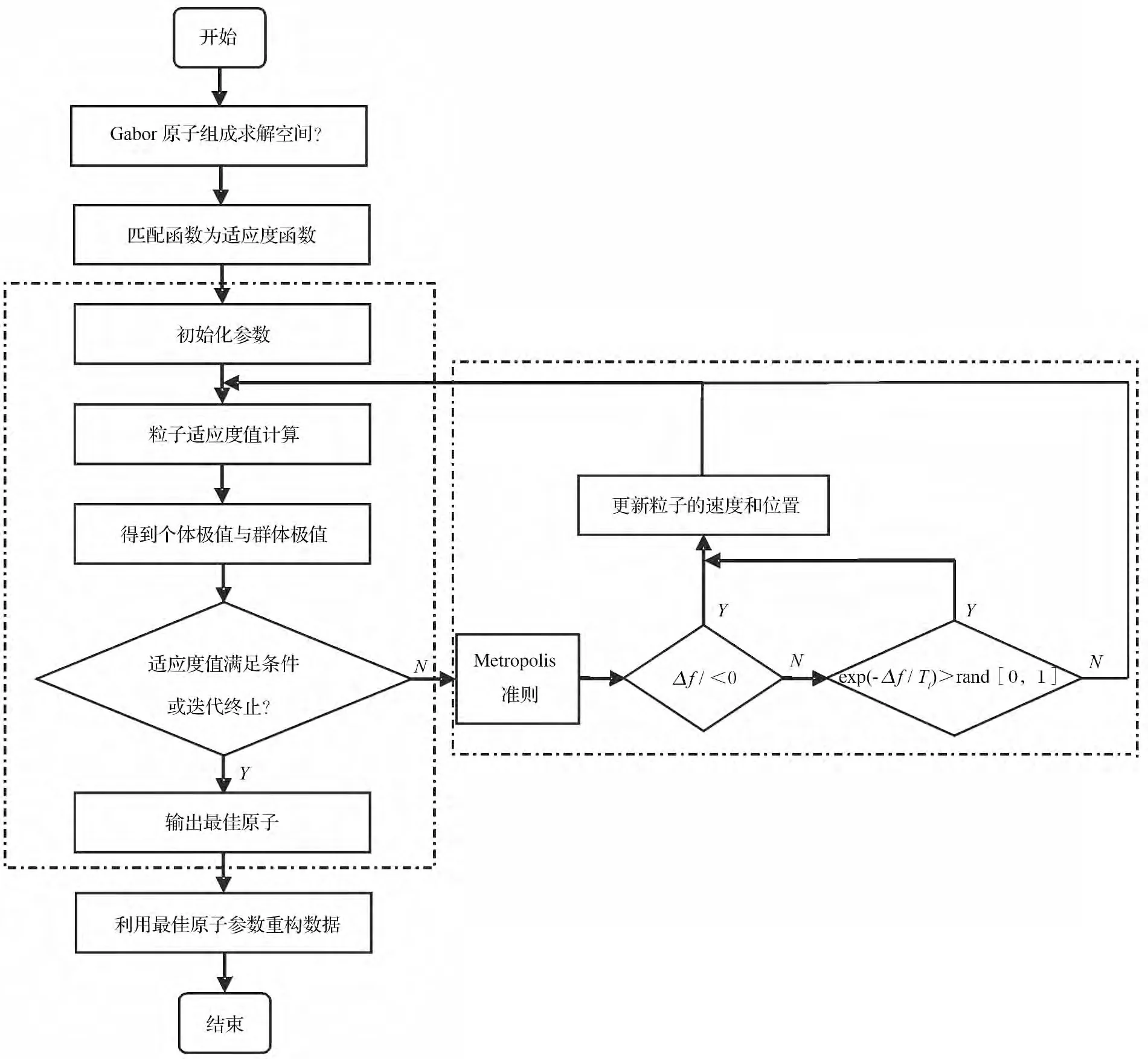
图1 PSO-SA-OMP 重构算法流程图
3 仿真实验及结果分析
3.1 重构参数设计
探地雷达模型如图2所示。XYZ 为探测空间,XOY 代表地表,XOZ 代表探测的地下剖面,发射天线(T)和接收天线(R)的距离为D,高度为l,根系上表面距地表的高度为h。当探地雷达在某一位置探测时,此时采集到的回波数据为A-scan 数据,回波中的唯一变量为时间;当探地雷达沿某一直线探测多次时,多道A-scan 数据组成B-scan 数据。
在XOZ 平面中,构造一个40 cm×40 cm 的二维目标空间,记作A,将其空间等分为L=1 600 个网格,记作A=[A1,…Ai,…AL]T,用b=[b1,…bi,…bL]T表示A 的加权系数向量,b 中的元素取布尔量,0 表示没有目标,1 表示有目标。
系统采用收发分置天线,天线距离地表高度l=15 cm,收发天线间隔D=3 cm,天线移动步长1 cm,系统对接收信号采样256 点,采样间隔10 ps,采用压缩感知的高斯随机矩阵满足均值为0,方差为1/,观测维数为128 维。粒子群和模拟退火中主要参数选择如下:种群大小为50,最大迭代次数为30,学习因子c1=c2=2.1,模拟退火初始温度T0=-fitness(gbest)/log(0.2),退火常数λ=0.2,选取50个原子重构信号。

图2 根系探地雷达模型图
3.2 A-scan 数据重构
按照参数设置,首先选取其中一组A-scan 数据进行实验。当发射波进入地面遇有目标时,信号幅度会发生变化。压缩感知信号重构效果,可以通过式(13)所示的均方误差(EMS)进行度量。

式中:N=256;f'(x)表示重构信号;f(x)表示原始信号。
图3是各类算法对A-scan 数据稀疏重构的对比。由图3a 得出,在信号长度50~256,原始数据受到杂波影响;而由图3b、图3c、图3d 可知,采用压缩感知后,仅保留了具有稀疏特性的目标信号,很大程度上去除了杂波的干扰。

图3 A-scan 数据重构方法比较
表1为各类算法的MSE 和运算时间。在Ascan 数据重构上,PSO-SA-OMP 算法的MSE 较小,但是PSO-SA-OMP 算法比传统OMP 算法运算速度明显提高,运算时间减少了10.471 s。
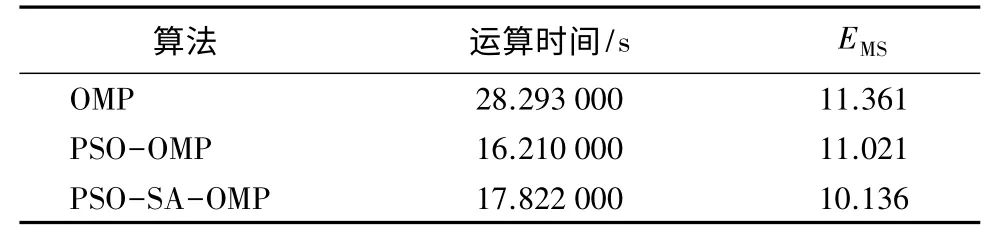
表1 A-scan 数据比较
3.3 B-scan 数据重构
多个A-scan 数据组成B-scan 数据。定义重构B-scan 数据图像的峰值信噪比RPSN,如式(14)所示。


图4 B-scan 数据重构算法比较
重构图像表明,PSO-SA-OMP 比传统OMP和PSO-OMP 重构的B-scan 数据图像更为精细,表2给出了PSNR 和时间的比较。PSO-SAOMP 重构算法不仅在PSNR 方面比传统OMP 算法提高了5.539 dB,而且运算时间减少了20.260 s;虽然PSO-OMP 算法运算速度更快,但是信噪比不高,本研究算法计算效率明显提高。

表2 B-scan 数据比较
3.4 复杂探地雷达数据重构
采用美国GSSI 实际采集的根系探地雷达数据进行测试,由上述实验已经得出,PSO-SA-OMP 重构算法在理想的仿真数据下不仅效果好,而且对杂波具有抑制作用。对于复杂的实际根系探地雷达数据,实验结果如图5所示。
图5a 和图5d 为实际数据图像,图5b 和图5e采用压缩感知理论的PSO-SA-OMP 算法对实际根系探地雷达数据进行重构。图5c 和图5f 为杂波抑制并进行图像二值化分割后得到的目标信息。分割图像表明,杂波能得到很好抑制,目标清晰。
4 结论
提出一种快速有效的根系探地雷达数据压缩感知重构算法,粒子群算法可以快速寻找OMP 过程中每一步分解的匹配原子,降低了运算复杂度,提高了重构的速度。模拟退火算法避免了收敛到局部最优,提高了信号重构精度。实验结果表明,PSO-SAOMP 算法能对探地雷达数据进行快速重构,降低了OMP 算法的计算复杂度与提高了重构精度,同时,优化算法具有杂波抑制作用,对于实际采集的根系探地雷达数据,能得到更加清晰的目标信息。

图5 PSO-SA-OMP 对复杂探地雷达数据测试
[1] Wu Y,Guo L,Cui X,et al.Ground-penetrating radar-based automatic reconstruction of three-dimensional coarse root system architecture[J].Plant and Soil,2014,383(1/2):155-172.
[2] Salvador J M,Jimenez V G,Lopez R,et al.Platform for research and education on ground penetrating radar[J].Radar Sensor Technology XVII,2013,8714(4):813-831.
[3] Raz-Yaseef N,Koteen L,Baldocchi D D.Coarse root distribution of a semi-arid oak savanna estimated with ground penetrating radar[J].Journal of Geophysical Research:Biogeosciences,2013,118(1):135-147.
[4] 郭立,范碧航,吴渊,等.探地雷达应用于植物粗根探测的研究进展[J].中国科技论文,2014(4):494-498.
[5] 卢策吾,刘小军,方广有.基于感知压缩的探地雷达数据压缩采集[J].电子学报,2011,39(9):2204-2206.
[6] 屈乐乐,黄琼,方广有,等.基于压缩感知的频率步进探地雷达成像算法[J].系统工程与电子技术,2010,32(2):295-297.
[7] Liu J,Xu S,Gao X,et al.Novel imaging methods of stepped frequency radar based on compressed sensing[J].Journal of Systems Engineering and Electronics,2012,23(1):47-56.
[8] 杨愚.利用粒子群算法实现信号OMP 稀疏分解[J].微计算机信息,2008,24(43):178-201.
[9] 张建军,王仲生,余汇.采用混合粒子群算法实现匹配追踪算法[J].振动与冲击,2010,29(1):143-147.
[10] 赵知劲,马春晖.一种基于量子粒子群的二次匹配OMP 重构算法[J].计算机工程与应用,2012,48(29):157-161.
[11] Bahmani-Firouzi B.A new hybrid algorithm based on PSO,SA,and k-means for cluster analysis[J].International Journal of Innovative Computing,Information and Control,2010,6(7):3177-3192.
[12] 于海平,刘会超,吴志健.基于模拟退火的自适应粒子群优化算法的改进策略[J].计算机应用研究,2012,29(12):4448-4450.
