不同曲率半径下曲线梁桥的地震时程分析

殷 超，赵 青

(安徽建筑大学 土木工程学院，安徽 合肥 230022)



不同曲率半径下曲线梁桥的地震时程分析

殷 超，赵 青

(安徽建筑大学 土木工程学院，安徽 合肥 230022)

为了分析曲率半径对曲线梁桥抗震性能的影响，以某城市一立交匝道曲线梁桥为背景，针对该匝道曲线梁桥，运用空间大型桥梁有限元分析软件Midas Civil，分别建立了五个不同半径下该曲线梁桥的有限元模型，探索不同半径下曲线梁桥的地震响应。采用E1 Centro地震波，只考虑桥梁的自重作用并采用多方向的地震动输入，进行了地震时程分析，研究了不同曲率半径下的曲线梁桥内力、位移的时程响应，并互相进行了比较，结果显示当自振频率比较小时，无论曲率半径如何变化，桥墩均出现弯扭，并且曲率半径对曲线梁桥的顺桥向和横桥向的地震响应均有较大影响。

立交匝道；曲线梁桥；不同半径；地震响应；时程分析

我国是一个多地震的国家，从公元前17世纪我国有最早期的地震记录开始,至今共有地震记录9 000多次,其中六级以上的破坏性地震就有800多次。而1901年至1969年我国六级以上的地震就有476次,平均每年多达6～7次。近年来,我国又陆续发生了多次七级以上大地震,如1976年河北唐山大地震、2008年汶川大地震等。各地交通部门在高速公路、城市立交建设中大量应用了曲线梁桥，这些曲线梁桥往往位于交通枢纽位置，重要性不言而喻。由于曲线梁桥，特别是小半径曲线梁桥，对于城市当中减少土地的占用、增加行车视野和美观有很大帮助，因此得到大量应用。文献[1-6]中分别对曲线梁桥进行了地震响应分析；文献[7-8]研究了支座设置对于曲线梁桥动力特性的影响；文献[9-10]从结构设计方面讨论曲线梁桥的抗震性能。本文以中部某城市一个立交匝道为研究对象，探索了在不同曲率半径下曲线梁桥的动力特性，并分析了不同曲率半径下曲线梁桥的时程响应曲线。

1 桥梁概况

某城市一个立交匝道曲线梁桥为等截面三跨预应力混凝土连续曲线箱梁桥，原桥本身位于半径为180 m的圆曲线上。跨径组成为29.5+30+29.5 m。桥梁上部结构为单箱双室截面，箱梁高度为2.9 m，桥面宽度为10 m，底板宽度为6.2 m，悬臂宽度为1.5 m，采用C50砼现浇。下部结构为两端双柱式桥墩，直径为1.4 m,中间为单柱桥墩，直径为2 m。墩高平均为10 m,均采用盆式橡胶支座。墩与承台均固结，采用钻孔灌注桩基础。桥梁类型为城-B类，场地类型为II类，抗震设防烈度为8°，特征周期为0.45 s。箱梁截面如图1所示，支座的布置形式如图2所示。

图1 箱梁截面图(单位：mm)

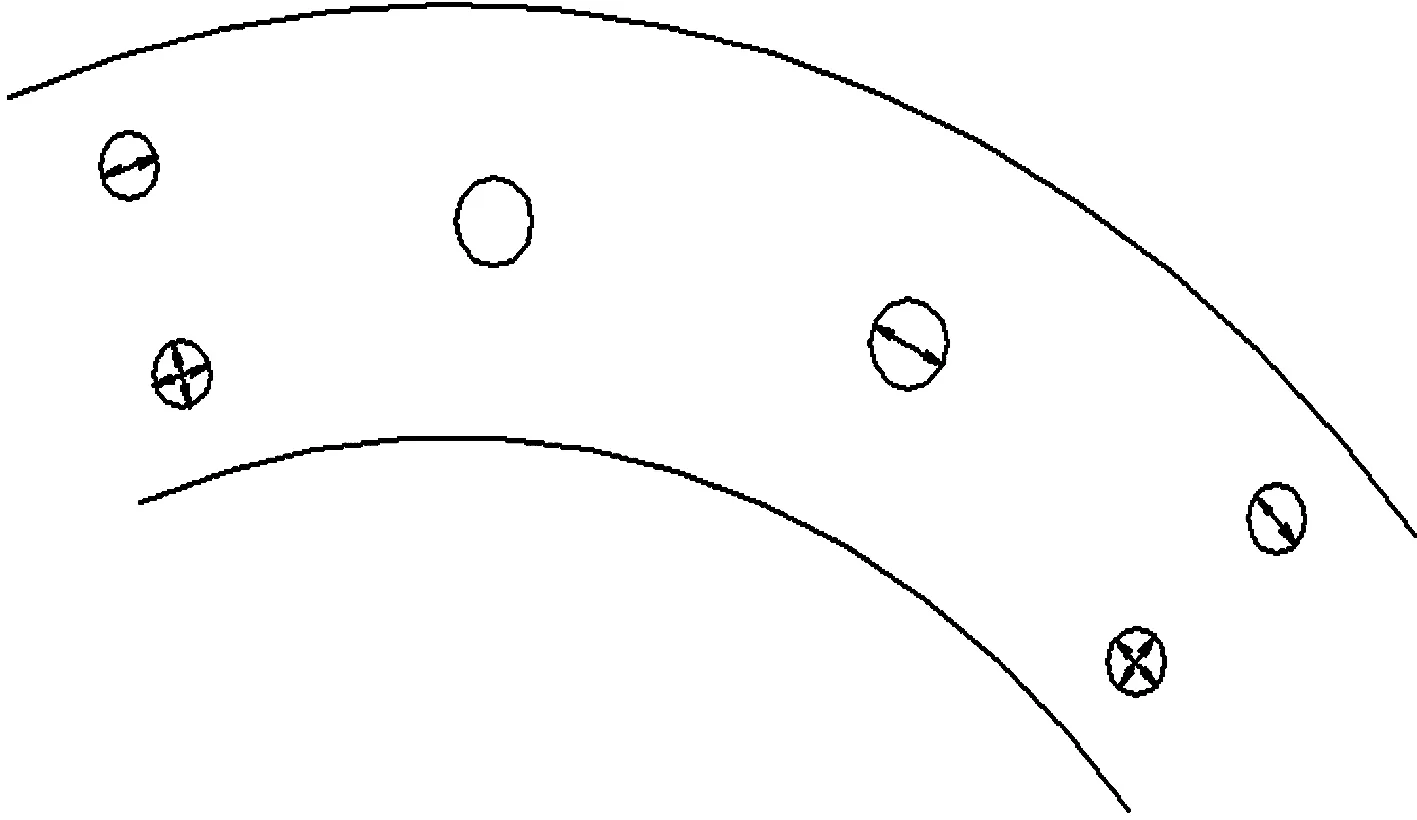
图2 支座布置形式

2 桥梁动力特性分析

为了研究曲率半径对曲线梁桥的动力特性的影响，本桥在建模过程中，曲线梁和桥墩均采用空间梁单元模拟，将墩底固定，并且不考虑桩土效应。在不改变桥梁结构以及支承形式的情况下，分别建立了曲率半径为30 m、60 m、120 m、180 m、360 m的5个有限元模型，采用Midas Civil程序中的多重Ritz向量法，对以上模型均进行了前十阶模态分析，探索其动力特性。原桥模型如图3所示。5个模型的前十阶自振特性如表1、表2所示。

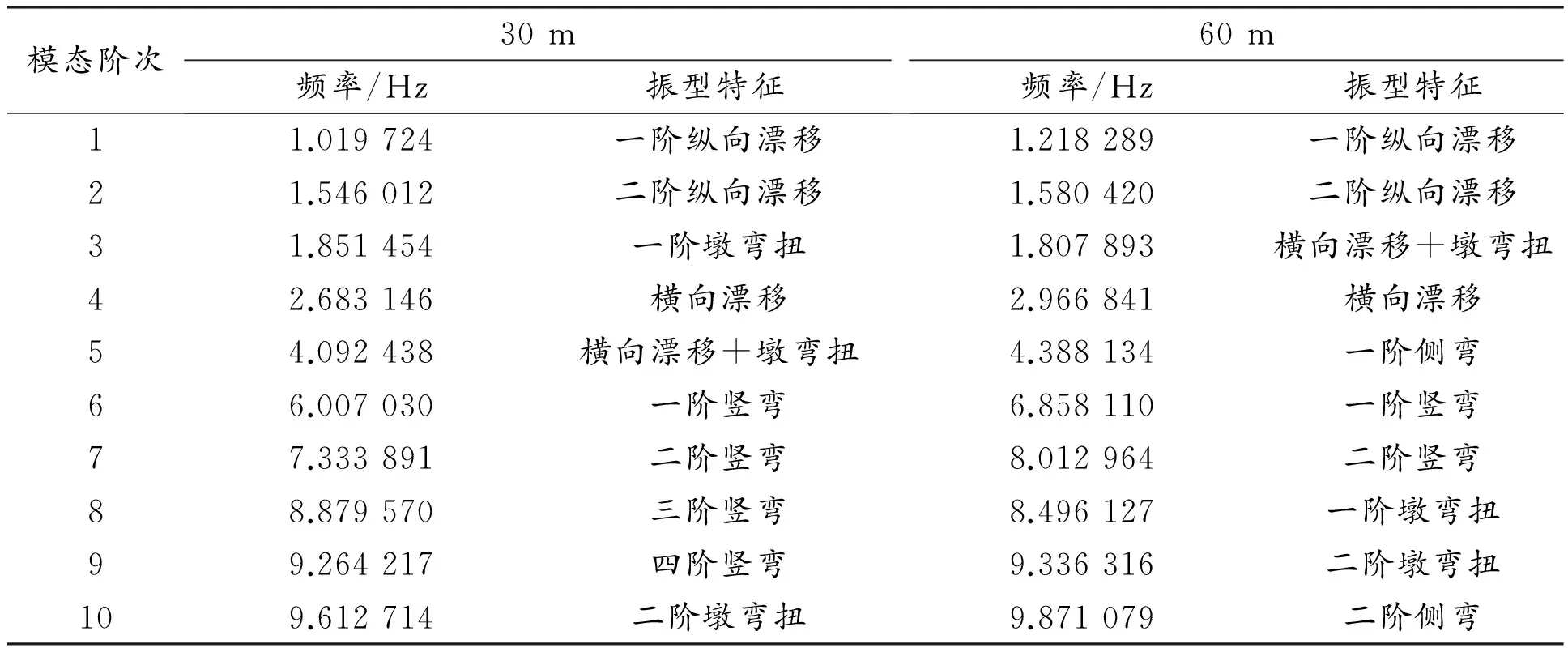
表1 曲线梁桥的自振特性(曲率半径分别为30 m、60 m)

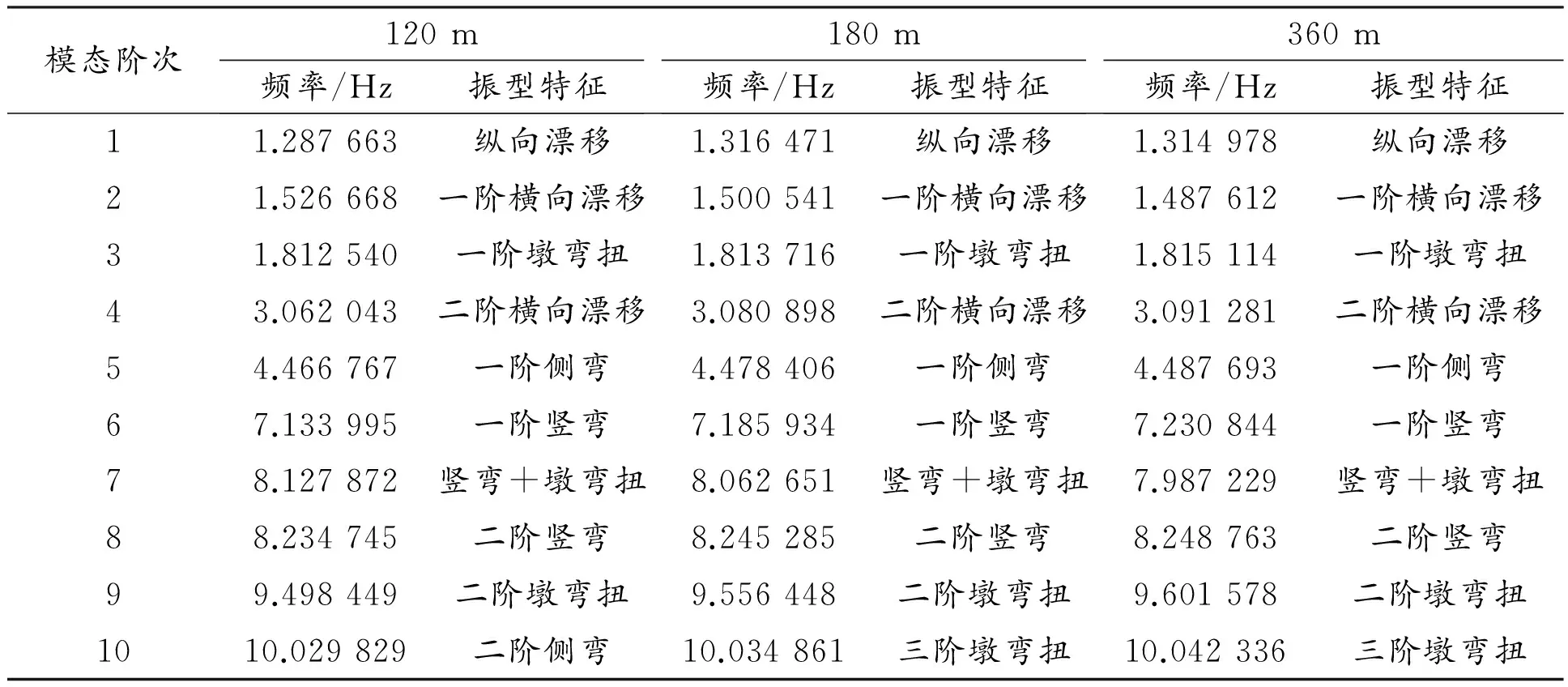
表2 曲线梁桥的自振特性(曲率半径分别为120 m、180 m、360 m)

图3 有限元桥梁模型

由表1、表2和图3可以看出：①当曲线梁桥的曲率半径比较小的时候，如半径为30 m、60 m时，第1阶和第2阶模态下，振型主要为主梁的纵向漂移，主梁无明显变形，而半径为120 m、180 m、360 m时，在第2阶模态下就出现了横向漂移，说明曲线梁桥的曲率半径越小，越有利于约束主梁的横向漂移；②前3阶自振频率均比较小的情况下，桥墩均呈现弯扭现象，说明不管半径如何，桥墩的刚度及曲线梁桥的弯扭耦合作用对曲线梁桥的动力特性影响均比较大；③在曲率半径较大的情况下，如曲率半径为120 m、180 m、360 m时，振型特征基本相同，而在曲率半径较小情况下，如曲率半径为30 m、60 m时，振型特征差别很大，说明半径增大到一定程度时，振型对桥梁的地震响应影响基本一致；④后面7阶自振频率较大的情况下，不论半径如何，均出现了箱梁侧弯、竖弯，墩弯扭等。

3 地震动的输入及调整

对于曲线桥梁，考虑到地震动在两个水平方向上存在耦合，所以不能只考虑顺桥向或者横桥向水平地震动的单向输入，而采用了地震波的双向输入[4]。本文选择了地震时程分析中最常用的E1 Centro地震波，顺桥向采用了1940, El Centro Site, 270 Deg波，横桥向采用了1940, El Centro Site, 180 Deg波，并且按照规范要求进行了调幅处理，持续时间调整为35 s，时间步长取0.02 s，地震加速度峰值取用0.2 g(g为重力加速度)。以曲线桥平曲线直线段方向为顺桥向，垂直于平曲线直线段方向为横桥向，将两个方向地震波在支承处沿桥横向按照一致激励方向输入，以得到结构的地震响应(见图4、表3)。

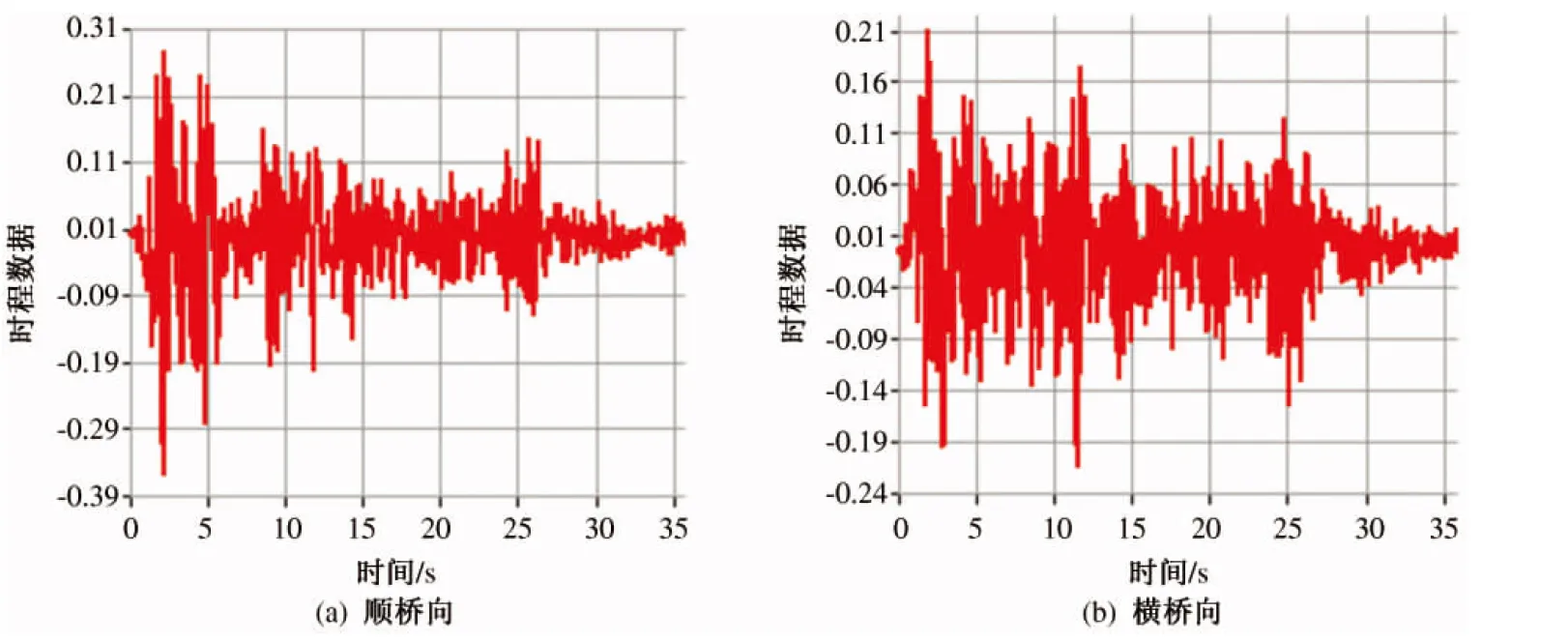
图4 E1 Centro 地震波

表3 地震波特性

4 地震响应分析

图5～图12分别给出了曲率半径为30 m、60 m、120 m、180 m、360 m的曲线梁和桥墩的内力和位移的地震时程曲线，并分别进行了比较。

图5 边墩顶位移

图6 中墩顶位移

图7 边墩底弯矩

图8 中墩底弯矩

图9 边墩底剪力

图10 中墩底剪力

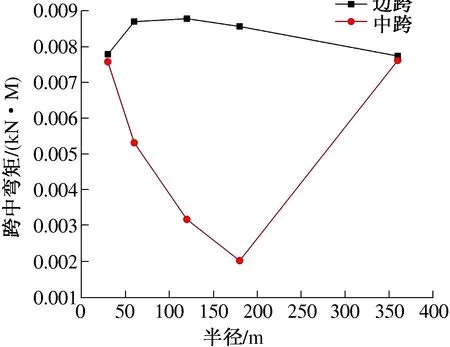
图11 跨中弯矩

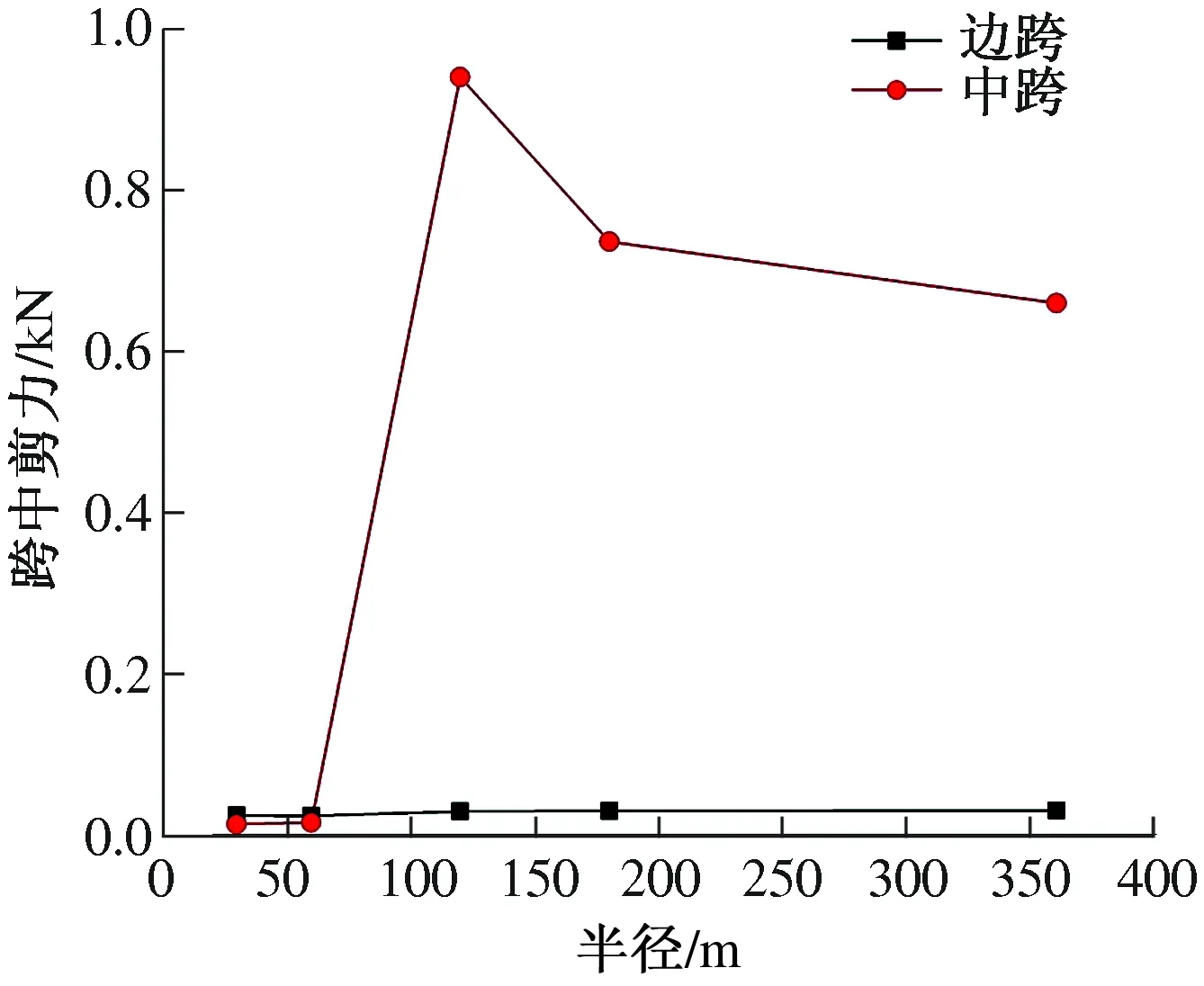
图12 跨中剪力

由图5和图6可以看出：边墩顶位移值在顺桥向随半径增大而逐渐增大，在横桥向随半径增大位移值先增后减，且横桥向位移值明显大于顺桥向位移值；中墩顶位移值在顺桥向随半径增大先增后减，在横桥向随半径增大位移值先减后增，且顺桥向位移值与横桥向位移值相差不大。由图7和图8可以看出：边墩底弯矩在顺桥向和横桥向随半径增大有减有增，但是顺桥向和横桥向弯矩值相差不大；中墩底弯矩在顺桥向和横桥向随半径增大也有减有增，但是顺桥向和横桥向弯矩值相差较大。由图9和图10可以看出：边墩底剪力在顺桥向随半径增大有增有减，在横桥向随半径增大逐渐减小，剪力值相差较大；中墩底剪力在顺桥向和横桥向均随半径增大而逐渐减小，但剪力值相差不大。说明曲率半径对曲线梁桥边墩和中墩顺桥向刚度和横桥向刚度均有较大影响。由图11和图12可以看出：边跨跨中弯矩随半径增大变化不大，而中跨跨中弯矩随半径增大变化较大；边跨跨中剪力随半径增大变化不大，而中跨跨中剪力随半径增大变化较大。说明曲率半径对中跨内力影响比边跨要大。

5 结语

依据有限元程序Midas Civil对某城市匝道曲线梁桥的动力特性分析和地震反应分析表明，其抗震性能有以下特点：

(1)对曲线梁桥进行动力特性分析，发现在自振频率比较小时，无论曲率半径如何，桥墩均呈现弯扭现象，而箱梁只是出现漂移，所以低阶振型下，桥墩变形比较大。

(2)在曲率半径较大时，振型特征基本相同，表明当曲线梁桥的曲率半径增大到一定程度时，曲率半径对桥梁的动力特性影响较小。

(3)半径对曲线梁桥的顺桥向和横桥向的地震响应均有较大影响。

(4)在实际曲线梁桥地震分析时，不能只采用单一方向的地震动输入，而应采用多个方向输入地震动，并对结果进行组合，以保证结构设计的安全性。

[1]戴公连,刘文硕,曾敏.小半径城市高架曲线梁桥地震动响应研究[J].振动与冲击,2012,31(2):155-160.

[2]曾敏.小半径曲线梁桥地震响应分析及减隔震研究[D].长沙:中南大学,2009.

[3]朱东生,刘世忠,虞庐松. 曲线桥地震反应研究[J].中国公路学报,2002,15(3):42-48.

[4]魏双科,李鸿晶,罗寒松,等.立交桥曲线箱梁动力分析模型[J].地震工程与工程振动,2006,26(4):168-175.

[5]王东升,孙治国,李晓莉.汶川大地震曲线梁桥震害及破坏机理分析[J],防灾减灾工程学报,2010,30(5):570-580.

[6]冯苠,李会驰,赵君黎.公路桥梁独柱墩结构安全风险综述[J].公路交通科技：应用技术版，2011(12):17-21.

[7]梁长海,杨成斌.支座布置对预应力混凝土曲线梁桥内力影响的研究[J].工程建设与档案,2005,19(5):393-396.

[8]方诗圣,肖兵,张吉烁,等.支座布置形式对曲线梁桥力学性能的影响[J].世界桥梁,2011(4):49-52.

[9]张平.曲线梁桥常见病害分析与设计优化[D].西安:长安大学,2013.

[10]李惠生,张罗溪. 曲线桥梁结构分析[M].北京:中国铁道出版社,1992.

Seismic time history analysis of curved girder under different radius of curvature

YIN Chao, ZHAO Qing

(DepartmentofCivilEngineering,AnhuiJianzhuUniversity,Hefei230022,China)

In order to analyze the influence of the radius of curve beam bridge seismic performance, taking an overpass ramp curve girder bridge as the background in a city. On the ramp curve girder bridge, by using the space finite element analysis of software Midas Civil, five different finite element model of the curved girder under the radius are established to explore the different radius of the curved girder Bridges under seismic response. The earthquake time history analysis is used with E1 Centro seismic waves and the weight of bridges and multi-direction of ground motion input is taken into account. The different curve radii of curvature of the beam bridge under internal force and displacement time history response are studied, and compared with each other. The results showed that when the natural frequency is relatively small, no matter how the radius of curvature change, piers are bending and torsion occurs, the radius of curvature and have a greater impact on the seismic response curve beam bridge along the bridge and the transverse direction.

interchange ramp; curve girder bridge; different radius; earthquake response; time history analysis

2015-09-07

安徽省高等学校自然科学研究重大项目(KJ2014ZD07)；安徽省高等教育振兴计划(2013ZDJY123)

殷 超(1989-),男, 安徽安庆人，硕士研究生。

1674-7046(2015)06-0012-05

10.14140/j.cnki.hncjxb.2015.06.003

U448.21

A