最大匹配问题Tile自组装模型

周 旭,周炎涛,李肯立,潘 果

(1.湖南大学 信息科学与工程学院, 湖南 长沙 410082；2.嘉兴学院 数理与信息工程学院,浙江 嘉兴 314001；3.湖南大学 电气与信息工程学院,湖南 长沙 410082)

最大匹配问题Tile自组装模型

周 旭1,2,周炎涛1,3†,李肯立1,潘 果1

(1.湖南大学 信息科学与工程学院, 湖南 长沙 410082；2.嘉兴学院 数理与信息工程学院,浙江 嘉兴 314001；3.湖南大学 电气与信息工程学院,湖南 长沙 410082)

Tile自组装模型凭借其自组装、可编程等特性在解决NP问题方面具有巨大优势.文中提出了一种求解最大匹配问题的Tile自组装新模型,该模型主要由初始配置子系统、选择子系统及检测子系统3大部分构成.新模型中首先设计Tile分子存储问题信息,其次通过Tile分子自组装操作生成最大匹配问题解空间,最后通过Tile检测分子筛选得到最大匹配问题的解.对模型从所需Tile分子种类、计算时间和计算空间3个方面进行性能分析,并通过实验模拟论证了模型的有效性和正确性.

DNA计算; Tile自组装模型; 最大匹配问题; NP完全问题; 并行计算

1994年,Adleman提出了DNA计算模型[1].此后,DNA计算以其具有的海量存储能力,巨大并行性及低能耗等特点,得到科学界的广泛关注.随着DNA计算的发展, 众多DNA计算模型被提出,主要有：粘贴DNA计算模型[2],表面计算模型[3],自组装模型[4]等.以上模型中,自组装模型以其自治性及纳米特性等优势,成为当前最具应用潜力的DNA计算模型之一[5].

随着生物技术的不断进步,Tile自组装模型自提出以来,得到了飞速的发展.Winfree基于Wang的Tile理论提出Tile自组装模型[4];Zhao等人提出了基于线性自组装的DNA加法算法[6]; Brun提出了基于Tile自组装的子集和问题算法[7];张勋才等人提出了一种基于自组装DNA计算的NTRU密码系统破译方案[8];方习文等人基于线性自组装模型提出了DNA减法模运算算法[9];周炎涛等人基于DNA自组装模型提出了一种求解最大团问题的算法[10].

图的最大匹配的DNA计算算法已有相当研究[11-12].然而文献[11]中提出的算法基于表面模型、文献[12]中提出算法基于粘贴模型，此两种模型均很难克服实验操作难度较大，需要大量的人工干预的缺点.此外,从公开发表的刊物看,关于最大匹配问题Tile自组装模型的研究还比较少.为此,本文对最大匹配问题Tile自组装模型进行了较深入的探索.主要工作如下:

1) 提出了一种最大匹配问题Tile自组装模型,该模型主要由初始配置子系统、选择子系统及检测子系统3大部分构成.

2)从所需Tile分子种类、计算时间和计算空间3个方面进行性能分析，并通过对算法进行实例模拟,进一步验证模型及算法的正确性和有效性.

1 Tile自组装模型

1.1 Tile分子的结构

基于Wang的Tile理论,1998年Winfree提出了一种Tile自组装数学模型又称为Tile自组装模型[4].Tile自组装模型中的Tile分子可以通过不同的DNA编码来构建.如图1所示,每个Tile分子可以抽象成为带有标签的四边形,每个标签可以识别不同的粘性末端.若两个不同的Tile分子的两个粘性末端互补,两个互补的粘性末端通过碱基互补配对连接进行Tile分子的自组装.本文将Tile分子定义为5元组.Tile分子分别通过North, South, West, East 4个

粘性末端存储信息,其中Value用来表示Tile分子代表的值(如图1).

图1 DNA Tile分子及其抽象模型

1.2 相关生物操作

本文模型在自组装模型中的基本生物操作如退火,连接,荧光标记及凝胶电泳操作的基础上,引入了Adleman-Lipton模型中抽取,检测,读取等生物操作, 具体描述见文献[12].

1.3 扩展的Tile自组装模型的抽象描述

对传统Tile自组装模型进行扩展[4].扩展后的Tile自组装模型定义为5元组, 其中g,t及Configuratio定义见文献[9],而TileSet及BioOperations定义如下：

1) TileSet, 表示自组装模型中Tile分子的集合, Tile分子的4个粘性末端可以表示不同的数值或计算过程中用到的符号.其中Tile分子定义如下.

①符号Σ表示Tile分子所有粘性末端标识的有限集合, null∈Σ.一个基本Tile分子可以用一个5元组<σValue,σNorth,σSouth,σWest,σEast>∈Σ5表示;

②Tile分子的位置用二维坐标(x,y)表示.假设某一Tile分子的坐标为(x,y),通过方向函数集Direction= {fNorth,fEast, fSouth, fWest}可以得到其相邻4个Tile分子的坐标,如fNorth(x,y)= (x,y+1), fEast(x,y)=(x+1,y), fSouth(x,y)=(x,y-1), fWest(x,y)=(x-1,y). 当位置(x,y)和(x′,y′)相邻时,满足条件d∈Direction,d(x,y)= (x′,y′).

2)BioOperations复制、退火、连接等生物操作[12].

2 最大匹配问题Tile自组装模型

2.1 问题描述

无向图G= (V,E)中具有顶点集V= {v1,v2,…,vn}, 边集E= {e1,e2,…,em}, 对E的任一子集M, 如果M中任意两条边ek,ed在G中没有公共的端点,则M为G的一个匹配.若G中没有另外的M’使得|M’|>|M|,则称M为G的最大匹配[12].图2包含的最大匹配分别为M1={e1,e3,e6}和M2= {e2,e4,e6}.

图2 具有6个顶点,6条边的简单无向图G

2.2 最大匹配问题Tile自组装模型

本文的最大匹配问题Tile自组装模型主要分为初始配置子系统, 选择子系统和检测子系统3个部分.

2.2.1 初始配置子系统

初始配置基本Tile分子抽象结构如图3所示. 生成大量如图3所示的初始配置Tile分子后,将通过本节的初始配置子系统生成最大匹配问题的初始配置.

图3 初始配置子系统中Tile分子抽象结构

定理1 定义∑s={p,C, |, =},初始配置子系统SystemInitial= ,其中Tinitial表示基本Tile分子的集合,ginitial=1,τinitial=2,BioOperations表示所需的生物操作.SystemInitial将生成最大匹配问题的初始配置.

证 初始配置系统SystemInitial中的基本Tile分子集合Tinitial={、<|, |,p, null>、、<|, null, null, =>、<|, null, = , null>和< null, |, =, null> }，其中1≤p≤m.初始配置子系统中通过将Tinitial集合中的Tile分子充分自组装后将生成初始配置Cinitial, 其中Cinitial中存在一些位置(x,y)∈2,满足如下约束：

1)∀(x=0,y=0),Cinitial(x,y)= <|, null,=, null > ;

2)∀(x=0, 1≤y≤n-1),Cinitial(x,y)= <|, |,p, null>, 其中1≤p≤m;

3)∀(x=0,y=n),Cinitial(x,y)= < null, |,=, null > ;

4)∀( -n+1≤x≤2,y=0),Cinitial(x,y)= ;

5)∀(x=n,y=0),Cinitial(x,y)= < |, null, null,= > ;

6) 对于其他的位置(x,y) ∈2, (x,y)∉Cinitial.

证毕.

2.2.2 选择子系统

基于2.2.1节中初始配置，通过本节的选择子系统基本Tile分子将生成最大匹配问题的初始解空间配置.选择子系统所需的基本Tile分子如图4所示.

图4 选择子系统中Tile分子抽象结构

定理2 定义∑C={C,Cp0,Cp1,p},选择子系统SystemChoose= ,其中Tchoose表示基本选择子系统Tile分子的集合,gchoose=1,τchoose=2, BioOperations表示所需的生物操作.SystemChoose将生成最大匹配问题的所有初始解空间配置,而在某一初始解空间配置基础上能够产生唯一的最终配置.

证 选择子系统SystemChoose中的基本Tile分子集合Tchoose={, 、< null,C, = ,=> }其中1≤p≤m. SystemChoose中通过将Tchoose中的选择分子自组装到初始配置Cinitial上生成初始解空间配置CInitialResult.CInitialResult中存在一些位置(x,y)∈2,满足如下约束：

1) ∀(x=0,1≤y≤n-1),CInitialResult(x,y)= 其中0．当边ep被选中时,i=1,CInitialResult(x,y)= , 其中1≤p≤m;

2)∀(x=0,y=n),CInitialResult(x,y)= ;

3) 对于其他的位置(x,y)∈2, (x,y)∉CInitialResult.

2.2.3 检测子系统

根据最大匹配问题的定义及Tile分子的基本生物特性,本节中设计了用于检测的Tile分子类型(如图5).

定理3 定义∑D={Cp0,Cp1,Cq0,Cq0,p, |, =},检测子系统SystemDetect=,其中Tdetect表示检测子系统中基本Tile集合,gD=1,τD=2.针对初始解空间配置CInitialResult,通过Tdetect中的检测分子能够检测出最大匹配问题的合法的DNA Tile组装体.

证 如图5,检测子系统SystemDetect中检测分子集合Tdetect={,,,,,,,,< null,Cp1, =, =>,< null,Cp0, =, =>,< |, |, null,Cq1>,< |, |, null,Cp0>,< |, null, null, =>,}其中1≤p,q≤m且p≠q.基于初始解空间配置CInitialResult,SystemDetect中通过将检测分子自组装到初始配置CInitialResult上生成最终配置Cfinal.Cfinal中存在一些位置(x,y)∈2,满足如下约束：

1) ∀(-m-1≤x≤-2, 1≤y≤m),Cfinal(x,y)=,,,,,,,;

2) ∀(-2≤x≤-m-1,y=m+1),Cfinal(x,y)= 或;

3) ∀(x=-m-2,1≤y≤m-1),Cfinal(x,y)= < |, |, null,Cq1> 或< |, |, null,Cq0>;

4) ∀(x=-m-2,y=0),Cfinal(x,y)= < |, null, null, =>;

5) ∀(x=-m-2,y=m+1),Cfinal(x,y) =;

6) 其他的位置(x,y) ∈2,Cfinal(x,y)=empty.

从以上分析可以发现∀t∈Tdetect,(bdsouth(t),bdwest(t)) 是唯一的,因此检测子系统SystemDetect中针对某一初始解空间配置CInitialResult将生成唯一的的最终配置Cfinal.

证毕.

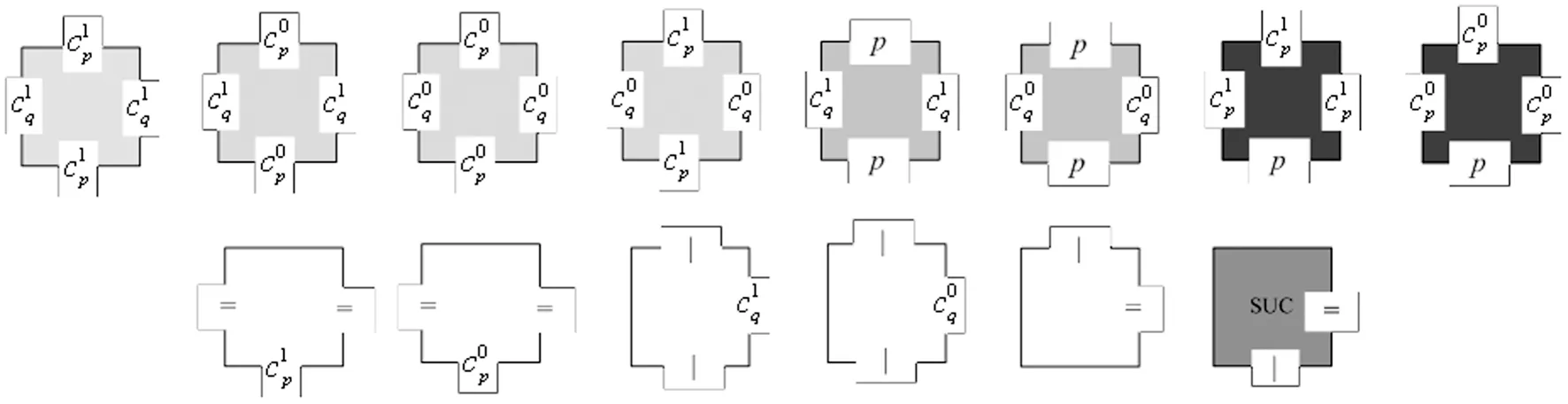
图5 检测子系统中的基本Tile分子

2.3 性能分析

本节将从所需Tile分子种类、计算时间及计算空间3个方面分析算法的性能.

引理1 Tile分子种类,计算时间和计算空间： 本文提出的最大匹配问题Tile自组装高效模型中,需要的Tile分子种类为O(m2), 计算时间为O(m),计算空间为O(m2).

证 本文模型主要由初始配置子系统、选择子系统及检测系统3个部分组成.其中初始配置子系统中需要Tile分子种类为2m+4; 选择子系统中所需的Tile分子种类为2m+1;检测系统中所需的Tile分子种类数为共为8m2-2m+2.综上分析可知本模型中所需Tile分子种类数为O(m2)；其次计算时间即自组装体的深度,本文模型中自组装体的深度为m+2,因而计算时间复杂度为O(m)；最后空间复杂度即Tile自组装体的面积,本文模型中自组装体的最大面积为(m+2)×(m+2),因而计算空间复杂度为O(m2).

证毕.

2.4 实验模拟

为了验证算法的正确性,借鉴文献[7]中的实验方法.以图G为最大匹配问题的实例.

2.4.1 Tile分子编码

以下将针对本文模型中的初始配置子系统，选择子系统及检测子系统3个部分,分别设计基本Tile分子：

1) 初始配置子系统中基本Tile分子有以下两类.① 针对每条边设计两类Tile分子：< 1, null, =, =>,< |, |, 1, null >,< 2, null, =, =>,< |, |, 2, null >,< 3, null, =, =>,< |, |, 3, null >,< 4, null, =, =>,< |, |, 4, null >,< 5, null, =, =>,< |, |, 5, null >,< 6, null, =, =>,< |, |, 6, null >; ②为了随后随机生成解空间，设计了Tile分子；③边界Tile分子<|, null, null , =>，<|, null, = , null>和< null, |, = , null>.

2)选择子系统中基本Tile分子有, ,,,,,,,,,,,< null,C, =, =>.

3) 检测子系统中基本Tile分子有检测分子, 信息传递分子及辅助检测分子3类.

①检测子系统中设计了如下检测分子用于传递边的信息，实现将初始配置中底端的边信息进行传递的Tile分子,其中p∈{1,2,3,4,5,6}; 主要用于辅助顶点信息的传递Tile分子,, ,其中p,q∈{1,2,3,4,5,6}且p≠q.

②检测系统中根据两条边是否具有相同顶点,设计检测分子.若被检测的两条边同时存在于初始配置中时,若边不具有相同的顶点,此时设计的检测分子有,,,,,,,,,,,,,,,;被检测的两条边中仅存在一条边存在于某一匹配方案中时,检测分子有, ,其中p,q∈{1,2,3,4,5,6}且p≠q;当前被检测的两条边均不存在于最大匹配中时,检测分子,其中p,q∈{1,2,3,4,5,6}且p≠q.

③一种边界分子主要用于辅助检测的同时输出结果.其中Tile分子有< null,C10, =, =>,< null,C11, =, =>,< null,C20, =, =>,< null,C21, =, =>,< null,C30, =, =>,< null,C31, =, =>,< null,C40, =, =>,< null,C41, =, =>,< null,C50, =, =>,< null,C51, =, =>,< null,C60, =, =>,< null,C61, =, =>,< |,|, null,C11>, < |,|, null,C10>,< |,|, null,C21>, < |,|, null,C20>,< |,|, null,C31>, < |,|, null,C30>,< |,|, null,C41>, < |,|, null,C40>,< |,|, null,C51>, < |,|, null,C50>,< |,|, null,C61>, < |,|, null,C60>, < |,null, null,=> 和.

2.4.2 求解过程

本文模型中的算法步骤可以分为Tile分子生成阶段、初始配置生成阶段、选择阶段、检测阶段和解的获取5个部分,具体求解过程如下:

1) 准备阶段.执行预处理算法,生成所需的基本Tile分子,分别存于试管Ttileinitial,Ttilechoose,Ttiledetect.

2) 初始配置生成阶段.试管Ttileinitial,通过Anneal()及Ligation()操作, Tile分子充分自组装得到初始配置(见图6).

3) 初始解空间生成阶段.合并试管Ttileinitial,Ttilechoose中大量Tile分子于试管Ttilechoose,通过Anneal()及Ligation()操作,Ttilechoose中的Tile分子充分自组装后得到初始解空间配置.如图7所示,分别展示了子图{e1,e3,e6}及{e1,e2,e6}对应的初始解空间配置.

4) 检测阶段.将存储检测Tile分子的试管Ttiledetect,存储初始解空间配置的试管Ttilechoose中的Tile分子及Tile自组装体进行合并后得到新的试管Ttiledetect.通过Anneal()及Ligation()操作,Ttiledetect中的Tile分子及初始配置充分地自组装得到最终配置.其中子图{e1,e3,e6}及{e1,e2,e6}对应的最终配置如图8所示.

图6 初始配置子系统生成的初始配置

5) 解的获取阶段：首先通过Extract()操作,抽取出试管Ttiledetect中含有tileSucc=的最终配置到试管TMatch中.利用Gel-electrophoresis()操作即凝胶电泳技术将试管TMatch中的最终配置按照长度进行分离.并通过Extract_ maxLength()操作,得到试管TMatch中最长的DNA Tile自组装体并存储于试管TmaxMatch中,Detect()操作检测试管TmaxMatch中是否含有DNA Tile自组装体,如果返回 ‘yes’,Read()操作读取试管TmaxMatch中的DNA Tile自组装体存储的信息,得到图G的最大匹配问题的最终解即{e1,e3,e6},{e2,e4,e6}.

3 结 论

随着生物技术的进步， DNA计算中的Tile自组装模型凭借其自组装,可编程等特性而得到广泛关注.然而, 据我们所知，现今公开发表的刊物上还未有关于最大匹配问题的DNA Tile自组装模型的研究.为此,本文首先提出了一种最大匹配问题的Tile自组装有效模型,模型主要分为初始配置子系统，选择子系统及检测子系统3大部分；其次基于提出的模型，设计了相关算法，并分析了算法的性能，通过算法模拟证明算法的正确性及有效性.

图7 选择子系统生成的子图{e1,e3,e6}，{e1,e2,e6}解空间配置实例图

图8 检测子系统生成的子图{e1,e3,e6},{e1,e2,e6}的最终配置实例图

[1] ADLEMAN L M. Molecular computation of solutions to combinatorial problems [J]. Science, 1994, 266(11): 1021- 1024.

[2] CHANG W L. Fast parallel DNA-based algorithm for molecular computation: Quadratic congruence and factoring integers [J]. IEEE Transaction on Nanobioscience,2012, 11(1): 62-69.

[3] LI D F, LI X R, HUANG H T,etal. Scalability of the surface-based DNA algorithm for 3-SAT [J]. BioSystems, 2006, 85(2): 95-98.

[4] WINFREE E. Algorithmic self-assembly of DNA [D]. Pasadena: California Institute of Technology, 1998.

[5] 杨静, 张成. DNA自组装技术的研究进展及难点[J]. 计算机学报, 2008, 31(12): 2138-2148.

YANG Jin, ZHANG Chen. Progress and difficulty in DNA self-assembly technology [J]. Chinese Journal of Computers, 2008, 31(12):2138-2148. (In Chinese)[6] ZHAO J, QIAN L L, LIU Q,etal. DNA addition using linear self-assembly[J]. Chinese Science Bulletin, 2007, 52(11): 1462-1467.

[7] BRUN Y. Solving NP-complete problems in the tile assembly model [J]. Theoretical Computer Scienee,2008, 395(l): 31- 46.

[8] 张勋才,牛莹,崔光照,等.基于自组装DNA计算的NTRU密码系统破译方案[J].计算机学报,2008, 31(12):2129-2137.

ZHANG Xun-cai, NIU Yin, CUI Guang-zhao,etal. Breaking the NTRU public key cryptosystem using self-assembly of DNA tilings [J]. Chinese Journal of Computers, 2008, 31(12):2129-2137. (In Chinese)

[9] 方习文,来学嘉.基于线性自组装的DNA减法模运算[J].科学通报, 2010,55(10):957-963.

FANG Xi-wen, LAI Xue-jia. DNA modular subtraction algorithm based on linear self-assembly[J]. Chinese Science Bull, 2010, 55(10): 957-963. (In Chinese)

[10]周炎涛, 李肯立,罗兴,等.一种基于DNA自组装模型求解最大团问题的算法[J]. 湖南大学学报:自然科学版, 2012, 39(9): 39-44.

ZHOU Yan-tao, LI Ken-li,LUO Xing,etal.An algorithm for solving maximum clique problem based on self-assembly model of DNA[J]. Journal of Hunan University:Natural Sciences,2012, 39(9): 39-44. (In Chinese)

[11]陈治平, 李小龙, 王雷，等. 最佳匹配问题的DNA表面计算模型[J].计算机研究与发展, 2005, 42(7):1241-1246．

CHEN Zhi-ping, LI Xiao-long, WANG Lei,etal. A surface-based DNA algorithm for the perfect matching problem[J]. Journal of Computer Research and Development, 2005, 42(7):1241-1246．(In Chinese)

[12]周旭, 李肯立, 乐光学, 等.一种最大匹配问题的DNA计算算法[J].计算机研究与发展, 2011,48(11):2147-2154.

ZHOU Xu, LI Ken-li, YUE Guang-xue,etal. A volume melecular solution for the maximum matching problem on DNA-Based computing[J].Journal of Computer Research and Development, 2011, 48(11): 2147-2154. (In Chinese)

Efficient Tile Assembly Model for Maximum Matching Problem

ZHOU Xu1,2, ZHOU Yan-tao1,3†, LI Ken-li1,PAN Guo1

(1. School of Information Science and Engineering, Hunan Univ, Changsha, Hunan 410082,China；2. College of Mathematics and Information Engineering, Jiaxing Univ, Jiaxing, Zhejiang 314001,China；3.College of Electrical and Information Engineering, Hunan Univ, Changsha, Hunan, 410082,China)

The characteristics of tile self-assembly model are nanoscale properties, self-assembly, programmable and so on, so it has a great advantage in solving NP problems. This paper proposed a new tile self-assembly model for maximum matching problem. The new model is composed of initial configuration subsystem, choosing subsystem and detecting subsystem. In the new model DNA tiles were designed to store the information. The solution space of maximum matching problem was generated through the assembly operation. Lastly, the answers were found out by the detecting tiles. The performance of the algorithm was also analyzed in terms of the assembly time, the computation space and the types of the tiles, and the algorithm was simulated to prove its effectiveness and correctness.

DNA computing; tile self-assembly model; maximum matching problem; NP-complete problem; parallel computing

1674-2974(2015)02-0114-07

2014-08-13

国家自然科学基金重点资助项目(61133005)，Major Research Project of National Natural Science Foundation of China(61133005); 国家自然科学基金资助项目(61173013, 61202109),National Natural Science Foundation of China(61173013,61202109); 湖南省杰出青年基金资助项目(12JJ1011) ; 浙江省教育厅科研计划项目(Y201226110); 湖南省科技厅科技计划项目(2013GK3082) ;湖南省教育厅资助项目(08D092)作者简介：周 旭(1983-)，女，江苏宿迁人，湖南大学博士研究生†通讯联系人，E-mail: yantao_z@hnu.edu.cn

TP301.6

A