基于实测电力噪声分布的窄带电力噪声建模

谷志茹，刘宏立†，谭周文，刘述钢

(1．湖南大学 电气与信息工程学院，湖南 长沙 410082;2．湖南科技大学 物电学院，湖南 湘潭 519000)

基于实测电力噪声分布的窄带电力噪声建模

谷志茹1，刘宏立1†，谭周文1，刘述钢2

(1．湖南大学 电气与信息工程学院，湖南 长沙 410082;2．湖南科技大学 物电学院，湖南 湘潭 519000)

基于实际测量电力噪声特性参数的统计分布，推导非高斯分布的窄带电力噪声模型，主要包括背景噪声和脉冲噪声.前者应用升余弦滚降滤波法建模，其功率服从正态分布；后者利用随机分布的特性参数：脉冲的宽度、间隔和包络所构建的脉冲函数来建模.宽度、间隔和包络随机量均服从分隔马氏链.然后应用实际测量数据和马尔克夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)分析法比较评估了此模型，数值分析结果显示，模型能够很好地逼近实际的电力噪声.

电力线通信; 智能电网; 正交频分复用；分隔马氏链；马尔克夫链蒙特卡罗

基于电力信道的通信技术是智能电网(Smart Grid)建设的主要通信方式.它不需要重新铺设专用的通信通路，通过在与传递电能同一路径的线路上确定通信链路来传递信息，并且电力线通信不会像无线通信那样容易被密集的建筑物所阻挡，从而减少安装和维护费用.电力线通信技术市场长期被单载波PLC技术所垄断.最近，被称为G3和PRIME标准[1]的OFDM窄带(10～95 kHz) PLC技术进入了市场.它提供高的通信速率，鲁棒的通信模式，这些是智能电网双向通信的关键.但是，作为信息传输媒介来进行数据或语音传输，低压配电网络具有负荷情况复杂、信号衰减大，信道容量小，并存在背景噪声、随机脉冲噪声、与工频同步的谐波噪声等.所以为满足智能电网双向通信的需求，以电力网络为信道的高速通信技术，必须有适应于电力信道的调制和编码方案，能够抵抗恶劣的信道属性等等，这都需要对实际电力线信道有深入的了解.

电力信道中影响高速通信的主要因素有因电缆损耗导致的信号衰减、多径传播和噪声等.其中多径传播在文献[2]中有详细论述，而应用于10～95 kHz的窄带电力线噪声的仿真模型还没有明确的推论.早期的研究显示电力环境中的噪声不是加性高斯白噪声(AWGN)[3].为了仿真噪声，许多文献提出了不同的噪声的统计模型，脉冲噪声的统计属性可以在文献[4]中发现；背景噪声的功率谱密度在文献[5]中建立；一种忽略脉冲噪声随机性的确定性窄带噪声数学模型在文献[6]中给出.然而，目前没有一种电力噪声模型，考虑了脉冲噪声在实际电力环境中包络和时间的分布.

由于电力噪声分布的多样性和随机性，用一种确定的数学模型很难体现其物理属性.本文通过构建真实电力线噪声的测量环境，记录并分析实测噪声，对其中的背景噪声和脉冲噪声进行了建模和仿真.前者的时域模型由高斯白噪声通过滚降系数为‘1’的滚降滤波器而得到，其功率近似服从正态分布；后者的时域模型由服从确定统计规律的特性参数所描述，特性参数根据实际测量的数据统计得到，其时域的仿真波形由MCMC分析得到.

1 噪声模型

根据背景噪声的平稳分布性和脉冲噪声的随机分布性，利用实际测量数据分别对两种噪声进行统计建模，再将两种噪声叠加[7]，得到实测的电力噪声模型.

1．1 噪声测量

文中所述噪声的测量均按图1所示系统实现.电力信号首先通过容性耦合器，将50 Hz的工频电压谐波噪声滤除，然后通过10～500 kHz的带通滤波器，得到窄带电力噪声，最后由大容量数据存储的数字采集器记录保存.滤波器采用3阶巴特沃斯带通滤波器[8]，线性中心频率为255 kHz.数字采集器的型号为USB2085，实现A/D转换和数据采集的功能，设置其采样频率为400 kHz，采集时长为10 min/次.

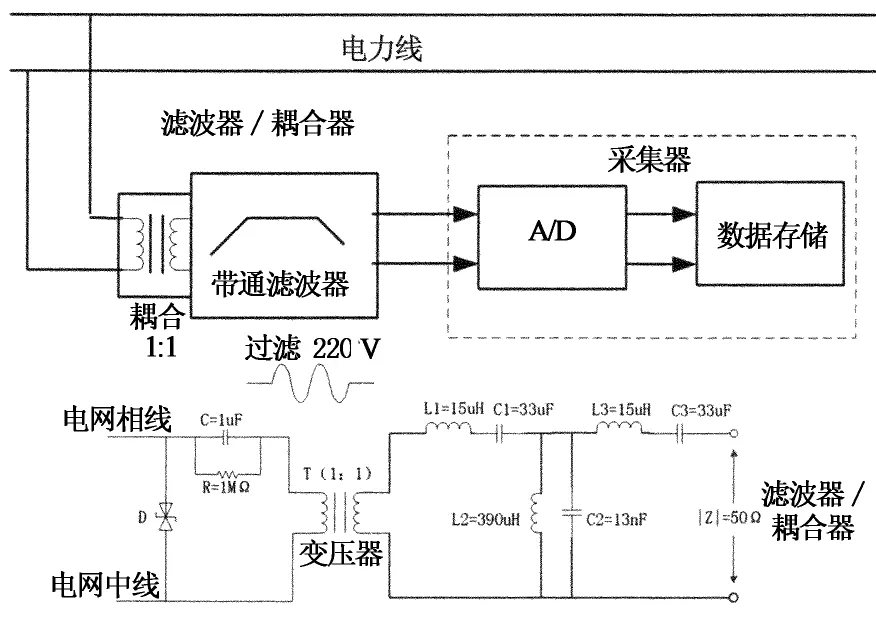
图1 测量系统

现选湖南大学13舍实验楼作为测试点，对七楼配电箱A相进行分时段的连续测量记录，根据用电负荷和噪声干扰的不同，分成3个时段进行测量:轻量噪声时段，00:00-06:00;中量噪声时段，12:00-13:00和重量噪声时段，14:00-17:00.测量总时长为6 361 min，约106 h.

1．2 背景噪声模型

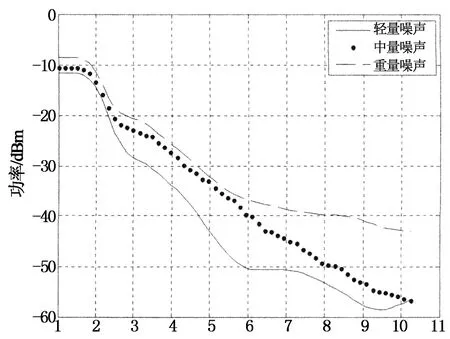
电力背景噪声属于平稳分布的彩色噪声，其功率主要集中于低频段.图2为去除窄带及脉冲噪声后背景噪声的功率谱密度，3个时段的噪声在频率最低处，功率最大，集中于-10 dB附近，随着频率的增大，功率减小，所以具有低通特性.因此背景噪声的时域模型ηc(t)，可以由加性高斯白噪声(AWGN)ξ(t)，通过滚降系数为‘1’的升余弦滚降滤波器而得到：

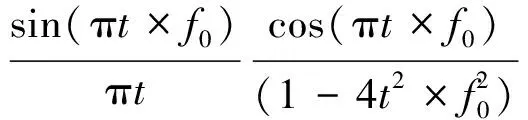
(1)

式中ξ(t)的功率谱密度为n0，通过测量数据的统计和中心极限定律分析[9]，n0近似服从高斯分布：n0～N(-10,2).升余弦滚降滤波器的参数f0，由背景噪声功率谱下降的速度决定.最低频点和最高频点功率的比值Pc，是滤波器在95kHz的频域值：

(2)

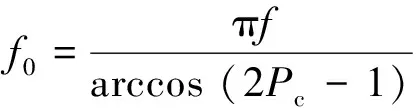
频率/(104 Hz)

1．3 脉冲噪声模型

脉冲噪声分为同步的周期性和异步的非周期性脉冲噪声.对于前者，因为具有确定性，所以建模相对简单；但是对于后者，因为时间和包络参数分布的随机性，所以必须用一个随机模型来描述，同时其特性参数服从确定的分布律.

1．3．1 脉冲噪声模型

图3为实测脉冲噪声的时域波形，显然，每个脉冲可由3个特性参数描述：包络av，宽度tw和间隔td.其脉冲函数表述如下[5]：

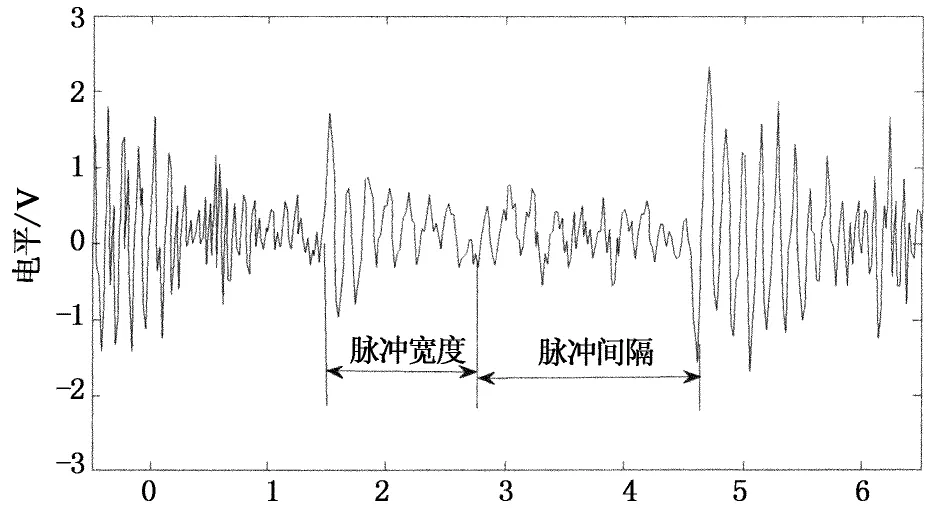
时间/ms

(3)

式中K是脉冲的总数;ta是脉冲噪声的到达时间，由脉冲的宽度和间隔决定.根据图3可知，脉冲噪声具有指数衰减的正弦波振荡特性，所以时域模型可由下式表示：

imp(t)=

(4)

在式(4)中，衰减因子d由脉冲噪声的宽度tw决定，表示脉冲下降的速度；振荡频率fosc决定了在一个脉冲宽度内，正弦波振荡的个数.令fosc=fs/2,

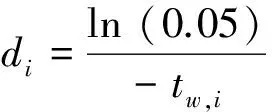
(5)

基于式(3)～(5)，特性参数tw，td，av和脉冲的总数K完全确定了脉冲噪声的时域波形，这些参数由时域测量数据的统计分析得到.

1.3.2 参数确定

这一节主要确定上节中所推得脉冲噪声的个数和特性参数的分布规律.

为确定脉冲的个数，取观察时长为1 s，定义在此时间内脉冲的总数为冲激率rimp，脉冲的总时长为干扰率dr，得到测量数据的统计值如表1所示.

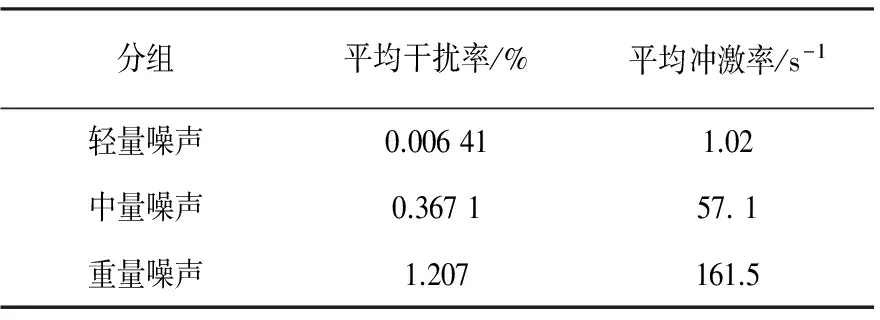
表1 测量数据的冲激率和干扰率统计

rimp和dr可以用下式表达：

(6)

式中NA和Np分别是异步脉冲和周期脉冲的个数.结合式(6)，表1可以通过脉冲的来源和数量来解释.在重量噪声时段，因为是工作时段，供电电源以同步于工频电压主频的速度持续动作，所以大量短时宽的周期脉冲占主导，即使脉冲的平均个数达到161个，但是所占时间仍然不足总时长的2%；在轻量噪声时段，实验楼内没有大量的用电设备，这时会有开关的瞬态过程，所以大部分是异步脉冲，周期脉冲可以忽略.因此在由“轻量噪声组”进入“重量噪声组”，周期性脉冲迅速增加.因为测量是在同一点位置进行的，所以3组时段异步脉冲的个数保持不变.基于此NA，NP和周期脉冲的tw_p可以推导如下：

(7)

式中rimp_wa和dr_wa是轻量噪声组的统计平均值，在表1中可以得到.

异步脉冲噪声的特性参数tw，td和av的测量统计见图4，其变化趋势近似服从指数分布，所以用分段马氏链[10]来描述，过概率(AdvancedProbabilitiesDensity,APD)如下：

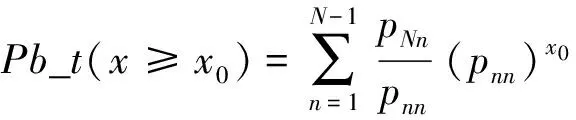
(8)

式中pNn和pnn是马尔克夫链的边沿和对角转移概率，x是时间离散化的值.令pr为边沿和对角概率的比值，对角概率为pd，则分段马氏链的概率密度函数可以由式(8)推得：

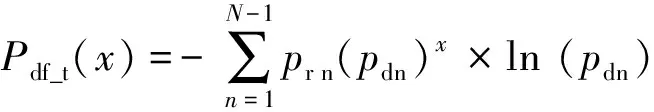
(9)

从式(9)可见，Pb_t和Pdf_t由加权指数函数构成，所以其系数pr和pd，可以通过最小二乘曲线拟合技术，从tw，td和av的测量统计值得到，如图4所示.

图4描述了轻量噪声组的特性参数概率分布，圈划线为测量统计，虚线是根据式(8)得到的,而直方图是对拟合的概率模型的仿真.由图4可见，脉冲噪声的统计模型，完全由实际环境的测量数据得到.而模型的仿真采样基于MCMC算法，因为所研究的窄带频段限制在10～95kHz，所以确定采样频率fs=0.4MHz，这正是窄带OFDM的采样频率.选取仿真时长为1s，则每个周期有4×105个样点.

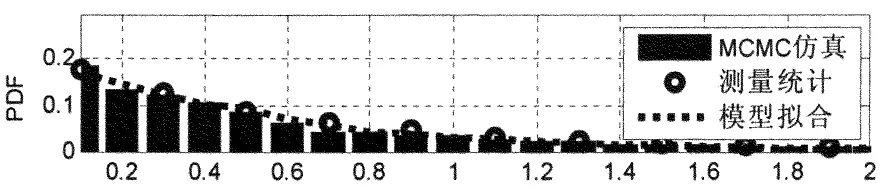
脉冲幅度/V

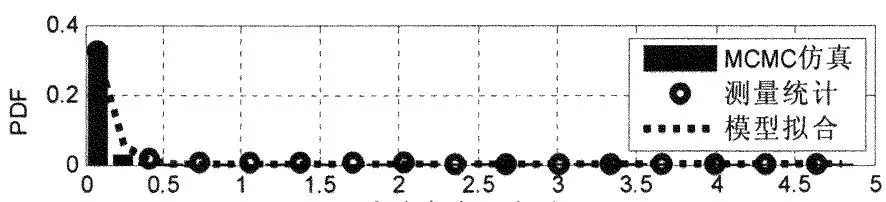
脉冲宽度/ms

脉冲间隔/ms

2 噪声仿真

电力噪声的仿真主要为背景噪声和脉冲噪声的仿真，再将两部分叠加，得：

η(t)=ηc(t)+ηimp(t)

其中背景噪声仿真主要是设计升余弦滚降滤波器，其截止频率由式(2)决定，功率谱密度由服从均值为-10，方差为2的正态分布的采样得到.

脉冲噪声的模型，因为参数是服从确定分布律的随机量，所以用MCMC能够得到快速收敛的仿真值.从图4可见，av和tw的测量统计具有快衰落的特点，在20个采样点后PDF(概率密度分布)已经低于10-4，所以用经典MCMC算法：Metropolis-Hastings(MH) 来仿真这两个量.画出仿真样点直方图，可以看出他们完全按照参数的概率分布模型抽取.

对于脉冲间隔td，概率密度分布于0～16 000ms，变化缓慢，包括200 000个样点，用经典MCMC算法很难达到收敛，所以采Multiple-Try-Metropolis(MTM) 算法[11]，与经典MH算法比较，在不降低接受率的条件下，MTM具有更大步长的跳跃.这种算法首先产生几个相关样点，然后从中选择一个最优点.在这种算法中，目标分布和提议分布分别是概率密度函数Pdf_t(x)和正态分布函数N(x).为得到新的采样，给定初始值为x0.一般，在MCMC算法的权重函数中给出更多的统计信息，能够改善仿真的性能.所以权重函数构造如下：

(10)

接受函数和权重函数之间的关系是：

(11)

则MTM算法的步骤如下：

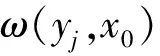
3 模型评价

为了验证提议的模型，将实际电力噪声的测量值与提议模型的仿真值进行比较.在重量组选择5组具有不同(rimp,dr)的测量数据，仿真时长设置为20s.根据每组(rimp,dr)，仿真100组基于提议模型的随机噪声，统计仿真组的(rimp,dr)和均方功率[12]，并与测量值比较.

图5为相同(rimp,dr)条件下，测量值和仿真值的时域波形和功率谱密度，从图中可见，时频域波形比较接近.基于测量数据及仿真数据的干扰率和均

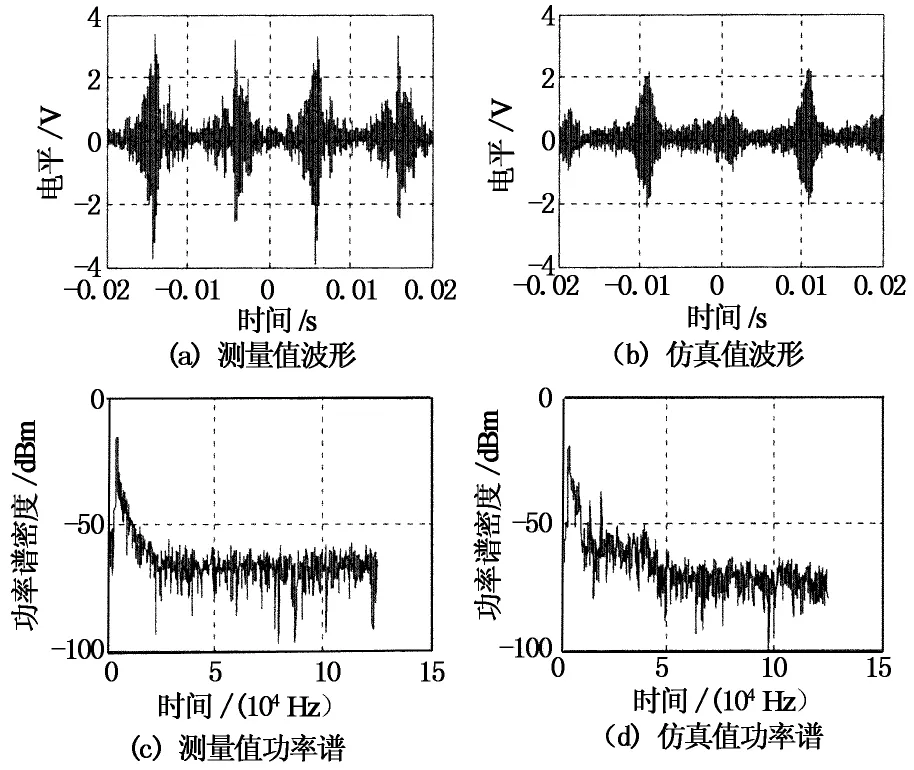
图5 测量值和仿真值的时频域波形比较

方功率的比较如图6所示.横坐标是冲激率，纵坐标是干扰率和均方功率，仿真数据的均方功率曲线和干扰率曲线很好地拟合了测量数据的相应曲线.

图6 测量值和仿真值的冲激率和均方功率比较

为使评价更加完善，现选取应用比较多的ClassA噪声模型，使其与提议模型和实际测量的APD相比较.ClassA模型的APD定义如下：

(12)

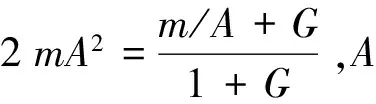
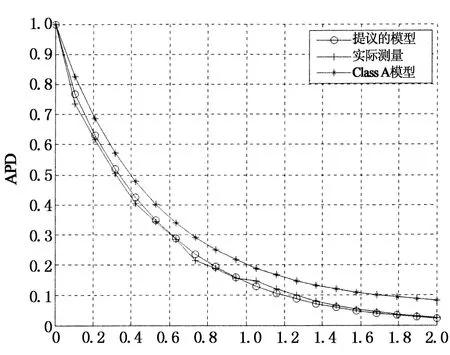
图7为Class A模型、提议模型和实际测量数据的APD比较，测量噪声选取轻量噪声时段数据.因为这一时段的噪声主要是异步非周期性脉冲噪声和背景噪声，所以其APD曲线比较平滑，对实际测量的APD应用EM 算法[13]，确定Class A模型的参数：A=0.5,G=0.1，利用式(8)得提议模型的参数.从图7可见，提议模型的APD与实测数据更为接近.

从以上对不同模型的比较评价，提议模型均能更好地逼近实测数据，所以在研究窄带电力载波通信技术时，可以用提议模型仿真实际的电力线噪声.

幅度/V

4 结 论

电力线环境作为通信信道时具有非高斯分布的噪声特性.因此应用高斯噪声作为信道干扰，进而设计和评价电力载波通信算法，其实质并不适应于电力线环境.为此本文根据实际测量电力噪声的统计分析，提出基于随机分布的特性参数所描述的随机模型.其中背景噪声模型由AWGN通过升余弦滚降滤波器得到；脉冲噪声模型由脉冲包络、宽度和间隔所限定的随机模型得到.通过MCMC算法仿真，得到模型的实现，最后通过与实测数据的比较证明了所提议的模型可以用来仿真实际的电力线噪声.

[1] JAVIER M, SADOT A, RODRIGUEZ-MORCILLO C. Performance evaluation of two narrowband PLC systems: PRIME and G3 [J].Comput Stand Inter, 2013, 36(1): 198-208.

[2] ZIMMERMANN M, DOSTERT K. A multipath model for the power line channel [J]. IEEE Trans Commun, 2002, 50(4):555-559.

[3] GOTZ M, RAPP M,DOSTERT K. Power line channel characteristics and their effect on communication system design [J]. IEEE Communications Magazine, 2004, 42(4):78-86.

[4] ZIMMERMANN M, DOSTERT K. Analysis and modeling of impulsive noise in broad-band powerline communications [J]. IEEE Trans Electromagn Compat, 2002, 44(1): 249-258.

[5] HOOIJEN O G. A channel model for the residential power circuit used as a digital communications medium [J]. IEEE Trans Power Del, 2004, 19(3): 1057-1064.

[6] KATAYAMA M, YAMAZATO T, OKADA H. A mathematical model of noise in narrowband power line communication systems [J]. IEEE J Sel Area Comm, 2006, 24(7): 1267-1276.

[7] ANDREADOU N, PAVLIDOU F N. Modeling the noise on the OFDM power-line communication system [J]. IEEE Trans Power Del, 2010, 25(1): 150-157.

[8] YAO S N,COLLINS T,JAN P.Hybrid method for designing digital butter worth filters[J]. Comput Electr Eng, 2012, 38(4): 811-818.

[9] MORRIS H DeGroot, MARK J Schervish. Probability and statistics[M]. 3rd ed. New York:Addison-Wesley, 2002: 219-237.

[10] THOMAS Kaijser. On Markov chains induced by partitioned transition probability matrices [J]. ActaMathematica Sinica, 2011, 27(3): 221-227.

[11] MARTINO L, DEL Olmo V P, READ J. Amulti-point metropolis scheme with generic weight functions [J]. Statistics and Probability Letters, 2012, 82(7): 121-134.

[12] 于善奇. 统计方法引论 [M]. 第2 版.北京：北京工业大学出版社，2014:251-267.

YU Shan-qi. Introduction to statistical methods [M].2nd ed. Beijing: Press of Beijing University of Technology, 2014:251-267.(In Chinese)

[13] CHEN Shu-chuan, LINDSAY Bruce. Improving mixture tree construction using better EM algorithms[J]. Computational Statistics & Data Analysis, 2014, 74(5): 17-25.

Modeling Narrow-band Power Line Noise Based on Distribution of Field Noise Measurement

GU Zhi-ru1, LIU Hong-li1†, TAN Zhou-wen1, LIU Shu-gang2

(1．College of Electrical and Information Engineering, Hunan Univ, Changsha，Hunan 410082，China;2．Physics and Electronic Science, Hunan Univ of Science and Technology, Xiangtan,Hunan 519000,China)

Based on the distribution of measurement, a Non-Gaussian model of narrow-band power line noise including background noise and impulsive noise was derived, The background noise, which follows Gaussian distributions, was modeled with a raised cosine roll-off filter, while the impulsive noise was modeled with impulse width, interarrival times and envelope parameters, whose distribution follows partitioned Markov chain. Then, the model was evaluated with some field measurement data and the Markov Chain Monte Carlo (MCMC) analysis. The evaluation results show that the proposed model can approximate the noise in real environment.

power line communication; smart grid; orthogonal frequency division multiplexing; partitioned Markov chain; Markov Chain Monte Carlo

1674-2974(2015)02-0081-06

2014-07-26

国家自然科学基金资助项目(61172089),National Natural Science Foundation of China(61172089)；高等学校博士学科专项科研基金资助项目(20120161120012)；湖南省科技计划资助项目(2014WK3001)

谷志茹(1979-)，女，河南开封人，湖南大学博士研究生†通讯联系人，E-mail:hongliliu@vip.sina.com

TPN14

A