基于应变模态法的层合梁的损伤检测研究

张 琼，毛贻齐，官 邑，陶 昶

(湖南大学 机械与运载工程学院，湖南 长沙 410082)

基于应变模态法的层合梁的损伤检测研究

张 琼†，毛贻齐，官 邑，陶 昶

(湖南大学 机械与运载工程学院，湖南 长沙 410082)

结构在建造和服役期间将不可避免出现损伤，发展合适的无损检测方法对其进行检测具有广泛的工程应用价值.基于多自由度振动力学和连续体损伤理论，发展了应变模态法损伤检测理论.通过预置损伤复合材料层合梁的动态加载试验，测得各个测点的应变时程响应，然后利用MATLAB编程对数据进行处理，从而得到结构的损伤应变模态曲线.数据处理结果精确反映了预置结构损伤的位置，由此证明了应变模态法能够应用于复合材料层合梁的损伤定位.最后基于有限元软件ABAQUS，利用连续体损伤理论对损伤纤维金属层合梁的模态进行分析，更进一步验证了当前应变模态法对损伤层合的损伤定位的可靠性.

应变模态；无损检测；纤维金属层合梁；损伤

结构在建造过程与服役期间将不可避免的出现损伤.在初始阶段，损伤表现为微小裂纹，一般难以发现，随着微小裂纹的演化，损伤将表现为可见的裂缝、脱层等，这将轻则影响结构的力学性能，重则导致结构完全失效而引发重大事故发生，造成人员伤亡和经济损伤.因而，检测结构损伤的大小及位置，评估结构的整体性能，从而对结构及时进行有效的维护，具有重要的工程实际意义.

随着振动理论、计算机技术及信号处理技术的发展，结构损伤检测技术的有效性与应用领域不断增长.根据检测目标不同，可以将损伤检测分为两类，一是局部检测，比如：X射线技术、超声波技术、无线电成像技术等；二是整体检测，比如：频率法、结构矩阵修改法、神经网络法、应变模态法等.根据应变具有对损伤敏感的特点，通过比较损伤结构和完好结构的应变模态变化来判断结构损伤大小和位置，即为应变模态法.相较于传统的检测手段，应变模态法对损伤检测非常有效，且可以检测结构内部损伤以及工作人员无法到达位置的损伤，从而成为工程应用及科学研究的热点.

通过对混凝土矩形简支梁进行位移与应变模态实验，顾培英和丁伟农[1]发现应变模态相较于位移模态对损伤灵敏度更高，且应变模态对非节点损伤非常敏感；徐丽[2]对框架结构进行应变模态实验研究，分析了一阶和二阶应变振型对识别损伤存在、位置的灵敏度；通过仿真计算，邓焱和严普强[3]发现应变模态明显地反映损伤存在、大小及位置，同时低阶模态振型由于其较易获得，从而在实桥检测中受到更多关注.周先雁等[4]应用应变模态法对钢筋混凝土结构损伤识别进行了初步尝试，根据损伤状态下的动应变相对于完好状态下的变化量进行损伤定位.王文静等[5]通过对悬臂梁结构进行位移模态分析、应变模态实验分析及有限元计算，验证了三者识别的模态参数基本一致，而且应变模态分析方法可以确定结构应变最大点和共振疲劳危险点.基于应变模态变化率，赵才友等[6]对钢轨的损伤位置及损伤程度进行研究.包振明等[7]采用光滑应变模态差分曲线诊断梁结构的非贯穿损伤.更多的研究[8-12]利用应变模态，对不同材料和结构进行了无损检测，但目前应变模态法主要应用于均质材料的损伤定位分析，鲜有文献报道应变模态法用于非均质材料，如复合材料的损伤检测分析.

本文首先对应变模态法的理论进行了介绍，理论上证明了采用应变模态法对损伤进行检测的合理性.然后，通过对预置损伤复合材料层合梁进行动态加载，利用MATLAB编程处理试验数据，从而得到结构的损伤模态曲线.试验结果精确反映了预置结构损伤的位置，从而证明了应变模态法对复合材料层合结构损伤检测的准确性.最后，基于损伤理论，利用有限元软件ABAQUS对损伤纤维金属层合梁的模态进行分析，进一步证明了采用应变模态法对复合材料层合结构损伤检测的可靠性.

1 理论模型

1.1 损伤理论

(1)

而损伤变量 基于材料弹性模量的改变来描述，即

(2)

式中Ei0和Gi0分别为无损材料在3个材料主方向上的弹性模量和剪切模量；Ei和Gi分别为具损伤材料在3个材料主方向上的弹性模量和剪切模量，且G4=G13，G5=G23，G6=G12.

Qd=M-1·Q·(M-1)T

(3)

其中，Q为无损材料的弹性刚度张量.考虑平面应力状态情况，假设损伤主方向与材料弹性主方向相同，由方程(3)，得到正交各向异性材料的损伤弹性刚度矩阵为:

(4)

1.2 应变模态法介绍

由振动力学理论可知，连续体梁式结构的位移响应u为:

{u}=[φr][Yr][φr]T{F}

(5)

式中φr为位移模态振型;F为激振力;Yr=(-ω2mr+jωcr+kr)-1.

按照梁的弯曲理论，应变是位移的一阶导数，故应变响应εx为:

(6)

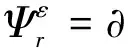
三维空间问题中3个方向的位移向量为[uvw]T，根据弹性力学原理，当仅考虑正应变时，其应变ε为：

(7)

写成矩阵形式即为:

(8)

因此可以定义[He]为力—应变传递函数矩阵，若只考虑一维小位移，得应变传递函数矩阵为:

[Hε]=[ψx][Yr][φ]T

(9)

式(9)还可以表示为:

(10)

式中{rψx}表示在x方向第r阶应变模态振型，{rφw}表示z方向第r阶位移模态振型.为了简便，将ψ和φ的下标x和w去掉，取式(9)中的任一元素来表示由激励点j到响应点i的应变传点函数为

(11)

令s=jω，且只取其中一个参数，即在e点激振，f点拾振，则对于第i阶模态的表达式为:

(12)

则有:

(13)

2 应变模态检测复合材料层合梁的损伤检测实验

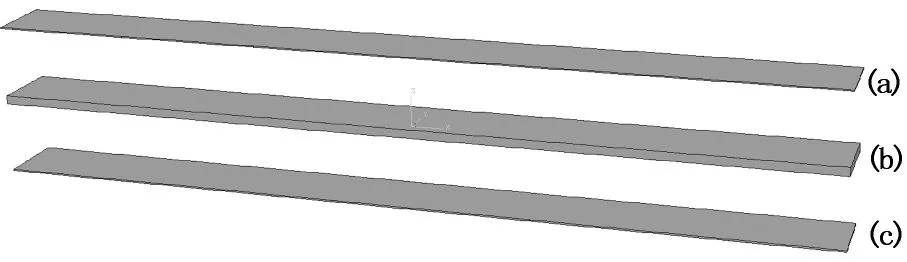
本节通过对损伤金属梁的动态应变检测，利用应变模态法对数据进行处理，并通过分析应变模态曲线找出结构损伤信息，以此证明应变模态法在损伤检测中的可行性.本实验设置了无损和有损层合复合材料梁，梁的几何尺寸均为600 mm×50 mm×8 mm, 边界约束均为一端固支，一端简支.为了进行损伤程度的对比，本实验设置了4根不同损伤程度的梁进行实验测试.损伤的预置为切割机切割出的一条表面割痕，位于距梁一端为163 mm处，割痕为梁横向贯穿(如图1所示)，损伤的宽度和深度分别为：0.3 mm×0.5 mm；0.3 mm×1.0 mm；0.5 mm×0.5 mm；0.5 mm×1 mm.在测试过程中，将梁沿轴向均匀分为9等份，在等分点上布置8个测点，并通过图2的8通道动态测试仪进行信号采集.

图1 预制损伤复合材料层合梁

图2 测试设备和数据采集

2.1 加载和数据采集

根据前面理论所述，在结构某固定点以r阶固有频率激振，测量激振力和该点的应变响应，将应变除以激振力，可获得应变传递函数的1列，再进行归一化处理后，获得第r阶频率的应变振型.实验过程中采用锤击方式加载，敲击方式为等时间间隔敲击，然后连续敲击，由此激励起结构尽可能多的模态.为了减少噪音影响，我们采用接地线处理，减少噪音影响，并通过调试仪器将噪音减少到可接受范围内.

2.2 数据分析

由各个测试点所得到的应变时程响应均包含了多阶模态，如果要得到各阶模态曲线，进行损伤分析，首先需要进行模态分离，再分别将数据拟合成各阶模态曲线.在模态分离时，将检测数据保存为TXT文件，然后导入MATLAB为后面的数据分析做准备.对于模态分离，本实验采取的方案是首先将数据进行幅频变换得到各个测点应变时程响应数据的幅频特性.由实验分析的不同测试点的各阶频率获取相应频率的振幅，然后通过插值法或者拟合法即可以得到对应于该阶频率的应变模态曲线.由于本文实验中结构损伤只是局部地影响结构，如果采用拟合法会掩盖这些局部的特征，因此，本文采取三次样条函数插值法来获取结构的应变模态曲线.

图3所示为采用应变模态测试得到的有损和无损纤维金属层合梁不同阶的应变模态位移.图中横坐标为测点号，纵坐标为归一化应变值(下同).由于梁两端均为面内不可动约束，其应变值取为零，结合所采集8个通道数据(如图所示共10个点)进行模态分析.本实验中仅测试了梁的纵向应变，其应变模态曲线由梁的纵向应变插值而成，因而无法反映出梁的面内扰动和扭转模态振型(第3，5，7阶模态)，

即损伤只能正确反映于第1，2，4阶应变模态(如图4所示).从第1，2，4阶有损和无损复合材料层合梁的模态曲线比较图中，可以看到在测点3附近模态曲线发生了变化.由于损伤的影响，结构的刚度被削减，从而导致结构的频率减小，相比无损情形，有损梁的模态在损伤区域发生了突变.从图中还可以看出，随着损伤宽度和深度的增大，模态位移的变化越明显，当损伤的宽度和深度为0.5 mm×1.0 mm时，模态位移在测试点3附近变化最明显.

测试点(a) 第1阶

测试点(b) 第2阶

测试点(c) 第4阶

3 数值分析与结果讨论

在检测纤维金属层合梁损伤实验前，先采用大型通用有限元软件ABAQUS对梁的模态进行计算，材料为铝夹层复合材料层合梁，梁夹芯为纤维增强复合材料，铝的材料参数设置为E=70 GPa，μ=0.3，ρ=2.5 g/cm3；纤维增强各向异性复合材料常数为E1=276 GPa，E2=6.9 GPa，E3=5.2 GPa，μ12=0.25，μ13=0.25，μ23=0.25，G12=3.4 GPa，G13=3.4 GPa，G23=3.4 GPa，ρ=2.9 g/cm3.在数值模拟过程中，纤维增强夹心层设置为15层；边界条件设置的是两端固支.

建模过程中，为了更加精确地模拟试验过程中的一边夹支和一边简支的边界条件，本文将模型夹支区域一端上下表面单元完全约束z方向位移模拟面内可动简支，另一端将上下表面单元三个自由度完全约束模拟夹支支撑 (如图4和5所示).对于梁的损伤和无损伤区域采用不同材料模型，对于具损伤区域，采用考虑损伤的材料模型，对于损伤判断采用强度破坏判据．

(a)上面板，(b)纤维铺层，(c)下面板

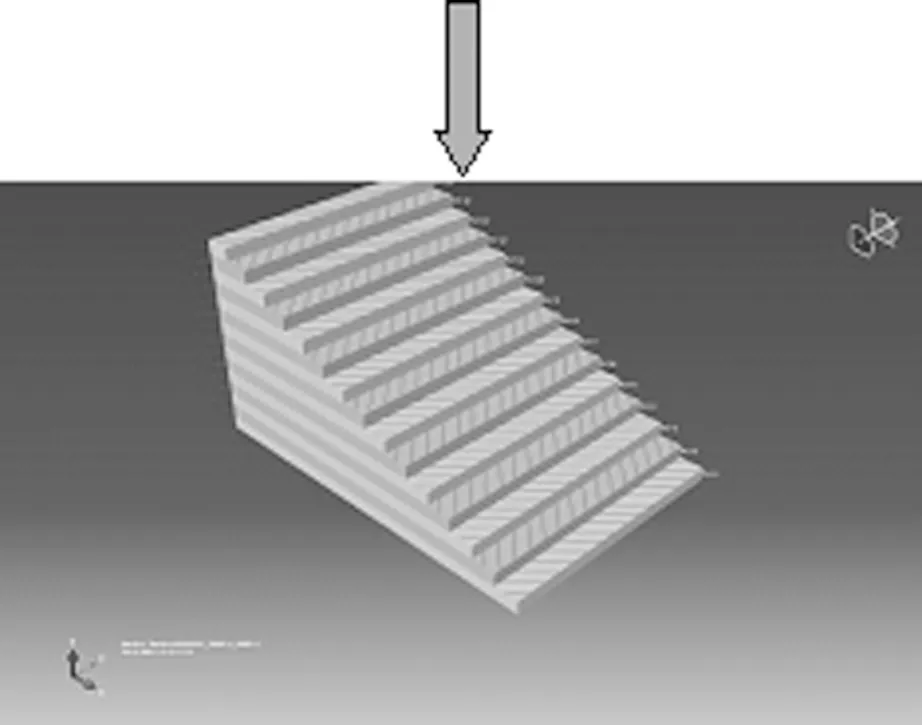
图5 纤维层铺设模型

第1阶

第2阶

第4阶

图6给出了有限元模拟的具损伤纤维金属层合梁的第1，2和4阶模态振型.在测试过程中模态曲线是由沿梁纵向应变插值而成，因此无法正确反映出梁的面内扰动和扭转模态振型，为了与实验测试进行对比，仅提取了有限元第1，2和4阶模态进行分析.表1给出了具损伤和无损伤的纤维金属层合梁的频率.表中显示了有损伤纤维金属层合梁的频率小于无损纤维金属层合梁的频率，这是由损伤导致梁的刚度降低造成的；且从图可以看出实验测试的数据与有限元结果吻合很好.

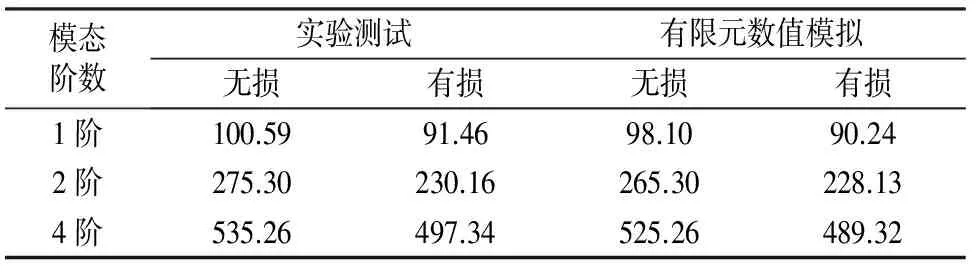
表1 由无损检测所得纤维金属层合梁的频率以及与有限元模拟结果的对比

图7和图8给出了当损伤尺度分别为0.5 mm×0.5 mm和0.5 mm×1.0 mm时的应变模态曲线.在分析模型中，通过削减该区域的刚度(弹性模量)模拟损伤的对结构力学特性的影响.在当前分析中，损伤区域的弹性模量取为无损区域的10%.从图可以看出，由于损伤的影响，材料的刚度削减，从而引起损伤区域应变模态的突变.从图可以看出，在测试点3附近，由于损伤的影响，在损伤位置出现应变集中效应，从而使应变模态发生突变，且损伤的影响在第一阶模态上反映更加明显；当预制损伤的尺度越大时，对应变模态曲线的影响更加明显.从图中可以看出，实验测试和有限元模拟所得应变模态的结果吻合较好，由此证明根据应变模态法可以有效地预测出结构的损伤区域.

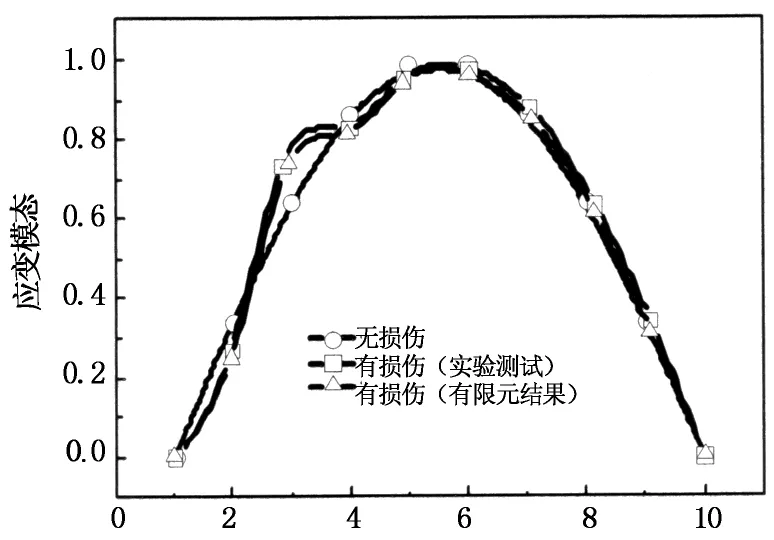
测试点(a) 第1阶

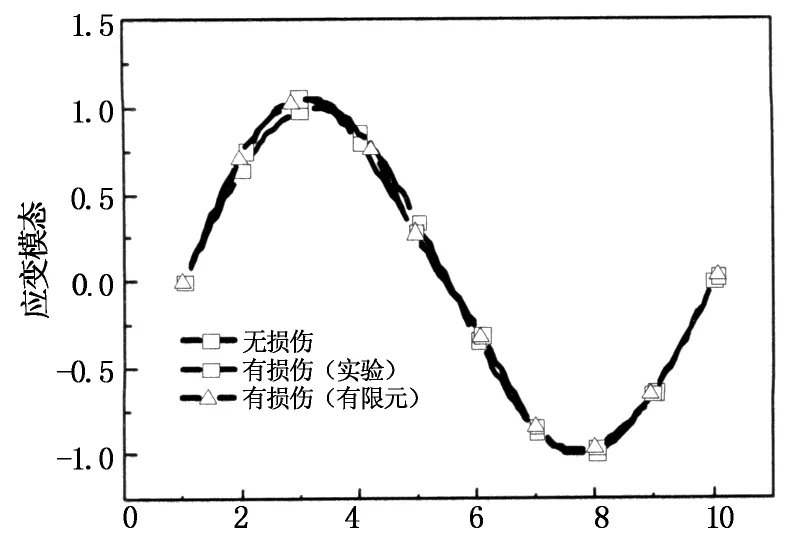
测试点(b) 第2阶

测试点(c) 第3阶

测试点(a) 第1阶

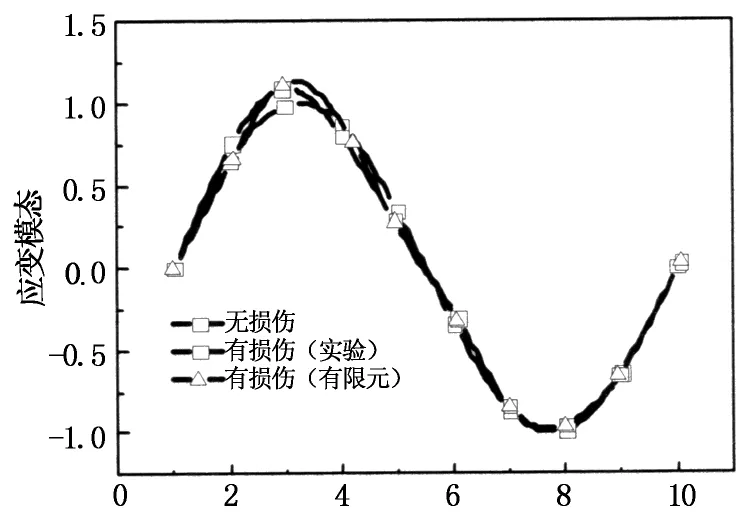
测试点(b) 第2阶

测试点(c) 第3阶

4 总 结

基于多自由度振动力学，本文通过预置损伤复合材料层合梁的动态加载试验，测得结构的损伤应变模态曲线.数据处理结果精确反映了预置结构损伤的位置，由此证明了应变模态法能够应用于复合材料层合梁的损伤定位.然后基于有限元软件ABAQUS，利用连续体损伤理论对损伤纤维金属层合梁的模态进行分析，更进一步验证了当前应变模态法对损伤层合梁的损伤定位的可靠性.从测试结果可以发现由于损伤的影响，损伤区域的应变模态曲线会发生突变，损伤导致的刚度削弱使得模态位移增加，而相应的结构频率降低.当预制损伤程度越大时，反应在应变模态曲线上的突变更加明显，因此，通过定量分析无损和有损应变对模态曲线的影响，可以定量地测试结构的损伤程度，这是我们接下来将开展的工作.

[1] 顾培英, 丁伟农. 模态试验在梁损伤诊断中的应用研究[J]. 振动与冲击, 2005, 23(3): 60-63.

GUPei-ying,DINGWei-nong.Applicationofmodaltestindiagnosingdamageofbeam[J].JournalofVibrationandShock, 2005, 23(3): 60-63.(InChinese)

[2] 徐丽. 框架结构节点损伤诊断的应变模态方法研究[J]. 广州大学学报: 自然科学版, 2005, 4(5): 423-427.

XULi.Investigationofstrainmodalmethodindamagedetectionofjointofframestructures[J].JournalofGuangzhouUniversity:NaturalScienceEdition, 2005, 4(5): 423-427. (InChinese)

[3] 邓焱, 严普强. 梁及桥梁应变模态与损伤测量的新方法[J]. 清华大学学报:自然科学版, 2000, 40(11): 123-127.

DENGYan,YANPu-qiang.Newapproachforstrainmodalmeasurementanddamagedetectionofbridges[J].JournalofTsinghuaUniversity:ScienceandTechnology, 2000, 40(11): 123-127. (InChinese)

[4] 周先雁, 沈蒲生. 用应变模态对混凝土结构进行损伤识别的研究[J]. 湖南大学学报: 自然科学版, 1997, 24(5): 69-74.

ZHOUXian-yan,SHENPu-sheng.Studyofdamageassessmentofconcretestructuresbystrainmodelmethod[J].JournalofHunanUniversity:NaturnalScience, 1997, 24(5): 69-74. (InChinese)

[5] 王文静, 刘志明, 缪龙秀. 基于实验模态的结构应变模态分析[J]. 北方交通大学学报, 2000, 24(4): 20-23.

WANGWen-jing,LIUZhi-ming,MIAOLong-xiu.Thestrainmodalanalysisofstructurebasedonmodaltesting[J].JournalofNorthernJiaotongUniversity, 2000, 24(4): 20-23. (InChinese)

[6] 赵才友, 王平, 全顺喜,等. 基于应变模态变化率的钢轨损伤检测[J]. 振动.测试与诊断, 2012, 32(5): 723-729.

ZHAOCai-you,WANGPing,QUANShun-xi,etal. Damage inspection of rail based on strain mode gradient[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 723-729. (In Chinese)

[7] 包振明, 马骏, 林哲,等. 简支梁损伤定位的直接指标法应用[J]. 船舶工程, 2013, 35(5): 79-82.

BAO Zhen-ming, MA Jun, LIN Zhe,etal. Application of direct index method of simply supported beam damage location[J]. Ship Engineering, 2013, 35(5): 79-82. (In Chinese)

[8] REN W X, DE ROECK G. Structural damage identification using modal data I: Simulation verification[J]. Journal of Structural Engineering, 2002, 128(1): 87-95.

[9] REN W X, DE ROECK G. Structural damage identification using modal data II: Test verification[J]. Journal of Structural Engineering, 2002, 128(1): 96-104.

[10]XIA Y, HAO H, BROWNJOHN J M W,etal. Damage identification of structures with uncertain frequency and mode shape data[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(5): 1053-1066.

[11]郭国会. 桥梁结构动力损伤诊断方法研究[D]. 长沙：湖南大学土木工程学院. 2001.

GUO Guo-hui. Research on damage diagnosis of bridge structures based on the vibration parameters[D]. Changsha: College of Civil Enginering,Hunan University, 2001. (In Chinese)

[12]李军, 于德栋, 白会人. 基于应变模态的结构损伤定位方法[J]. 世界地震工程, 2007, 23(1): 104-109.

LI Jun, YU De-dong, BAI Hui-ren. Damage localization of changes based on the strain modes for simply supported beam[J]. World Earthquake Engineering, 2007, 23(1): 104-109. (In Chinese)

[13]MURAKAMI S. Notion of continuum damage mechanics and its application to anisotropic creep damage theory[J]. Journal of Engineering Materials and Technology,1982;105:99-105.

Damage Detection of Composite Laminated Beam Based on Strain Model Method

ZHANG Qiong†，MAO Yi-qi，GUAN Yi，TAO Chang

(College of Mechanical and Vehicle Engineering, Hunan Univ, Changsha，Hunan 410082, China)

Micro-damage is always unavoidably incurred in structure in fabrication and serving performance. It is of high value to develop an undamaged detection method for these structures. Based on the multi-DOF vibration of mechanics and continuum damage theory, strain-mode based undamaged detection method was discussed and applied in the undamaged detection of composite beam. The strain response of the damaged laminated composite beam at different tested points was obtained through the dynamic test of the structures. And the strain-model curves of the damage structures was acquired by dealing with the dates with the MATLAB programs. The result indicates the exact position of the damage in the structure, which proves the validity of the strain-model method on the damage detection of the laminated composite structure. At last, the model analysis was conducted by applying continuum damage theory based on finite element software ABAQUS, which further demonstrates the feasibility and reliability of the strain-mode method in predicting the damage of structure.

strain mode; undamaged detection; fibre metal laminated beam; damage

1674-2974(2015)02-0060-07

2014-07-22

国家自然科学基金资助项目(11272117),National Natural Science Foundation of China(11272117)

张 琼(1961-)，女，湖南湘乡人，湖南大学高级实验师†通讯联系人，E-mail:zmj3647@hnu.edu.cn

TB333

A