船用齿轮箱多体动力学仿真及声振耦合分析

林腾蛟，何泽银，钟 声，刘 文，吕和生

(1.重庆大学 机械传动国家重点实验室，重庆 400044；2. 重庆齿轮箱有限责任公司，重庆 402263)

船用齿轮箱多体动力学仿真及声振耦合分析

林腾蛟1†，何泽银1，钟 声1，刘 文1，吕和生2

(1.重庆大学 机械传动国家重点实验室，重庆 400044；2. 重庆齿轮箱有限责任公司，重庆 402263)

基于多体系统动力学理论，综合考虑齿轮副时变啮合刚度、齿侧间隙、轴承支撑刚度等内部激励以及螺旋桨外部激励，建立了含传动系统及结构系统的船用齿轮装置多刚体系统动力学模型，计算了齿轮副动态啮合力及轴承支反力；对齿轮箱及支座进行柔性化处理，形成多柔体系统动力学模型，采用模态叠加法计算了箱体表面的动态响应.而后以多体动力学分析所得的轴承支反力频域历程为边界条件，建立了箱体声振强耦合分析模型，预估了齿轮箱表面声压及外声场辐射噪声.结果表明，齿轮副动态啮合力、轴承支反力以及箱体动态响应频域曲线的峰值均出现在齿轮副的啮合频率及其倍频处；仿真所得的箱体振动加速度及外声场辐射噪声与齿轮箱振动噪声试验台架实测结果吻合良好.

齿轮箱；多体动力学；声振耦合；动态响应；辐射噪声

齿轮传动具有承载能力大、寿命长、可靠性高、运转平稳等特点，广泛应用于船舶海洋、交通运输、冶金建材、工程机械等领域.随着科学技术的进步，齿轮传动正朝着大功率、高转速、低噪声方向发展，由于激励源多、激振频率高、啮合冲击大，振动噪声问题日渐突出，特别是船用齿轮装置，其动力学性能不仅影响到传动系统的可靠性，还影响到船舶的生命力和隐身性能，因此有必要针对船用齿轮箱开展振动噪声仿真及试验研究.

在齿轮系统动力学分析方面，国内外学者已做了大量的理论研究.考虑时变啮合刚度[1-2]、齿侧间隙[3-4]、啮合冲击[5]、轴承游隙[6]、齿面误差[7]等非线性因素，建立了齿轮系统动力学模型，研究了各种非线性因素对传动系统振动特性的影响.在齿轮箱辐射噪声分析方面，笔者以振动位移为边界条件，采用有限元法和边界元法建立了齿轮箱声学分析模型，计算了箱体的外场辐射噪声，并进行了振动噪声测试分析[8-9].以上文献得出了大量有价值的研究成果，但多数文献没有同时考虑齿轮系统内、外部激励的综合作用，分析对象仅局限于齿轮传动系统，未将传动系统和结构系统耦合求解，这无疑将影响齿轮系统动力学分析结果的准确性.目前基于声振耦合的齿轮系统振动噪声仿真研究已有少量成果[10-11]，但采用了简化的计算模型，难以准确预估齿轮箱的辐射噪声.

本文以船用齿轮箱为研究对象，综合考虑齿轮副时变啮合刚度、齿侧间隙、轴承支撑刚度等内部激励以及螺旋桨外部激励，建立含传动系统及结构系统的齿轮装置多刚体动力学模型，计算齿轮副动态啮合力及轴承支反力；而后对箱体及支座进行柔性化处理，以轴承支反力频域历程为边界条件，建立齿轮箱声振强耦合分析模型，预估齿轮箱表面声压及外声场辐射噪声，并与试验结果进行对比分析.

1 声振耦合分析理论与方法

声学Helmholtz波动方程为:

▽2p(x,y,z)-k2p(x,y,z)=-jρ0ωq(x,y,z)

(1)

在声场V中进行权重积分，并利用高斯理论转化为沿表面Ω法线方向n的积分，可得

(2)

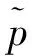
将声学刚度矩阵、阻尼矩阵、质量矩阵代入式(2)中，可得声学系统方程：

(Ka+jωCa-ω2Ma)·{p}={Fa}.

(3)

式中Ka,Ma和Ca分别为声学刚度矩阵、阻尼矩阵和质量矩阵；{Fa}为声学激励.

对于结构系统，动力学方程可表示为:

(Ks+jωCs-ω2Ms)·{u}={Fs}

(4)

式中Ks，Ms和Cs分别为结构刚度矩阵、阻尼矩阵和质量矩阵；{u}为位移；{Fs}为结构激励，包括结构的约束力及外载荷.

声音作用于结构上的声压载荷可看作是附加的法向载荷，故结构系统动力学方程可表达为:

(Ks+jωCs-ω2Ms)·{u}+Kc{p}={Fs}

(5)

式中Kc为耦合刚度矩阵.

在流体与结构耦合处，结构的法向振动速度与流体的法向振动速度应该一致，结构振动速度可看作是声场的附加速度边界，则调整后的声学系统方程为:

(Ka+jωCa-ω2Ma){p}-ω2Mc{u}={Fa}

(6)

式中Mc为耦合质量矩阵.

耦合刚度矩阵与耦合质量矩阵的关系如下:

(7)

将式(5)和式(6)写成矩阵形式的耦合方程为:

(8)

2 齿轮装置多刚体动力学仿真

2.1 多刚体动力学分析模型

船用齿轮箱各级齿轮副的基本参数如表1所示.在UG软件中建立船用齿轮装置的三维实体模型，如图1所示，图中的x,y,z方向分别为齿轮装置的横向、轴向和垂向.

表1 齿轮副的基本参数

(a) 传动系统

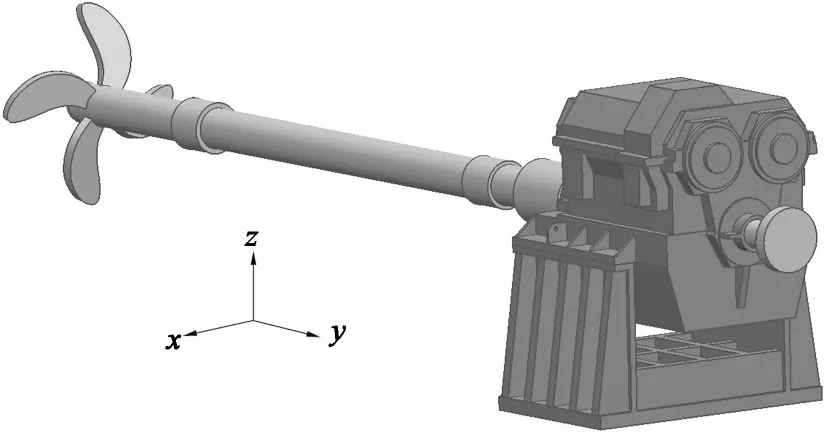
(b) 齿轮箱及安装支座

将齿轮装置实体模型导入到LMS Virtual.Lab软件的Motion模块中，设置各部件材料以便程序自动定义部件质心；在轴承座处设置“bushing force”，以定义轴承刚度和阻尼；在相互啮合的轮齿间设置“gear contact”，定义齿轮时变啮合刚度、阻尼、侧隙，以模拟齿轮副的啮合关系；在原动机处设置旋转副以定义输入转速；在螺旋桨处设置旋转副用于阻力矩的施加.

2.2 齿轮装置多刚体动力学仿真结果

综合考虑轮齿时变啮合刚度、啮合阻尼、齿侧间隙、轴承支撑刚度与阻尼及由输入输出波动引发的外部激励，采用变步长向后差分法(BDF)对齿轮装置进行多体动力学仿真.仿真时输入转速为750 r/min，波动范围设为5%；输出功率为400 kW，波动范围设为10%，波动形式均为正弦.求解总时间设定为6 s，时间步长Δt=6.25×10-5s.图2和图3分别给出了输入级齿轮副的动态啮合力和输入轴前轴承支反力曲线，图中时域曲线选取横坐标5.5～6 s的数据，频域曲线选取横坐标0～1 600 Hz的数据.

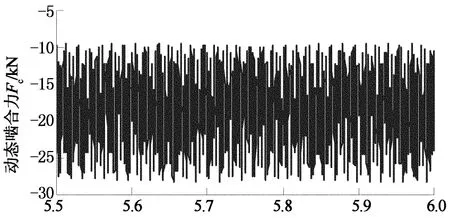
时间t/s(a) 时域曲线

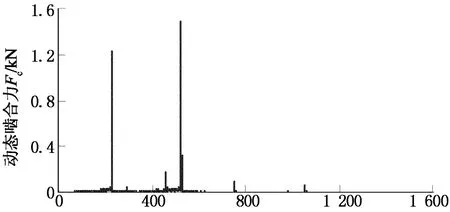
频率f/Hz(b) 频域曲线

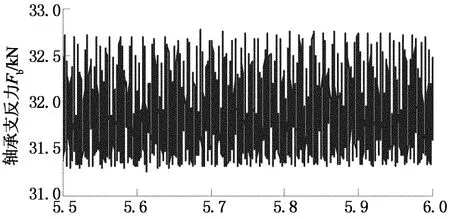
时间t/s (a) 时域曲线

频率f/Hz(b) 频域曲线

由图可知，齿轮副动态啮合力和轴承支反力主要受输出级啮合频率229.69 Hz及其倍频、输入级啮合频率525 Hz及其倍频的影响；相比齿轮啮合力，轴承支反力的频率成分更为丰富.

3 齿轮箱动态响应仿真分析

3.1 齿轮箱有限元网格

将图1所示的船用齿轮箱及安装支座导入Ansys中进行柔性化处理，定义单元类型Solid45，设置弹性模量、泊松比、密度等材料属性；采用自由网格和映射网格相结合的划分方法生成齿轮箱和支座的有限元网格，共计单元310 258个，节点183 586个，如图4所示，图中标注了支座处4个动态响应测点位置.

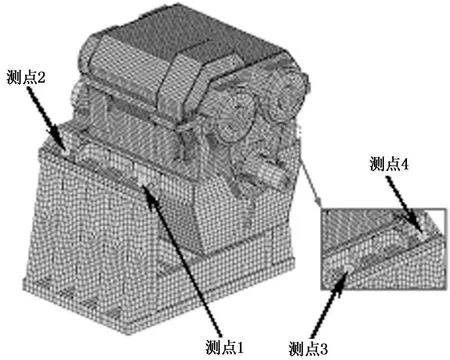
图4 船用齿轮箱有限元网格

3.2 齿轮箱模态分析

采用分块Lanczos法对船用齿轮箱进行模态分析，表2给出了前10阶固有模态频率.

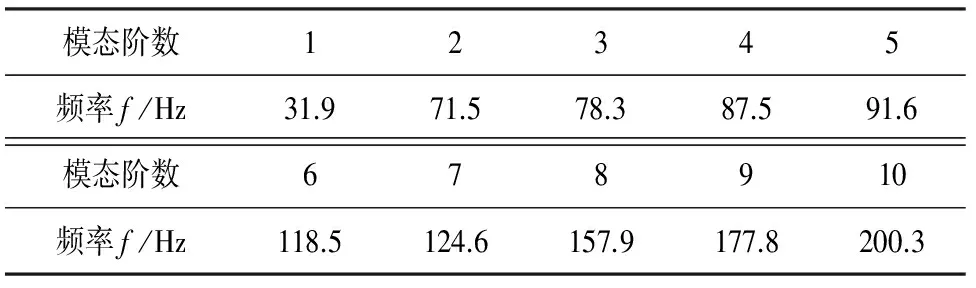
表2 船用齿轮箱前10阶固有模态

3.3 齿轮箱动态响应分析结果

将齿轮装置多刚体动力学分析所得的齿轮副动态啮合力施加在齿轮箱各级齿轮副上，在Virtual.Lab中采用模态叠加法计算齿轮箱动态响应，模态求解范围为0 ～ 4 000 Hz.表3给出了安装支座处4个测点的垂向振动加速度均方根值.

表3 垂向振动加速度仿真值

图5和图6分别给出了测点1的垂向动态响应时域和频域曲线.

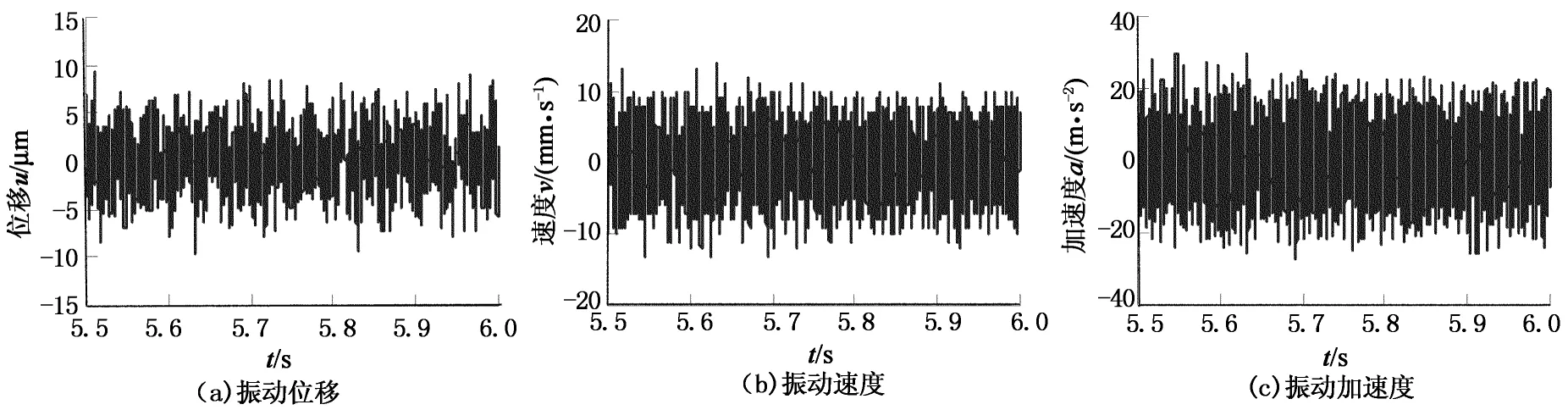
图5 测点1的垂向动态响应时域曲线

图6 测点1的垂向动态响应频域曲线

由频域曲线可知，在输出级齿轮副啮合频率229.69 Hz及其倍频处、输入级齿轮副啮合频率525 Hz处存在较大的峰值，表明齿轮副啮合频率对齿轮箱表面的动态响应有着最为直接的影响，为了达到齿轮箱减振降噪的效果，应从减小齿轮副动态啮合力的波动入手.

4 齿轮箱辐射噪声预估

4.1 齿轮箱声振耦合分析模型

为了减小计算规模，计算模型仅考虑箱体，未包含传动系统.建立声振耦合分析模型的要求是声学网格要完全包络结构网格，为此建立了一个空腔球形网格，球内部空腔表面尺寸完全与齿轮箱箱体匹配[12]，声学网格如图7所示.为了保证声学计算的准确性，通常要求在结构与流体交界面处一个波长内包含6个单元，为了同时兼顾计算时间与仿真精度，对辐射噪声的求解精度设定为4 000 Hz，声学网格共计单元1 014 368个，节点230 189个.声振耦合模型的边界条件为载荷激励，即将齿轮装置多体动力学分析所得的轴承支反力频域历程施加在箱体轴承孔处.

图7 船用齿轮箱声学有限元网格

4.2 齿轮箱表面声压及场点声压计算

齿轮箱周围声波传递介质为空气，空气密度为1.225 kg/m3，传播的声速为340 m/s，设定大气参考声压为2×10-5Pa，采用声振耦合有限元法求解，可得各计算频段处齿轮箱箱体表面声压云图.

图8给出了频率为500 Hz和1 000 Hz时的齿轮箱箱体表面声压云图.由图可知，当频率为500 Hz时齿轮箱表面声压已达137 dB.

为预估齿轮箱的辐射噪声，在齿轮箱外设置一矩形场点，矩形各面距离齿轮箱大约为1 m，如图9所示.图10给出了齿轮箱外场点辐射噪声声压云图.由图可知，频率为500 Hz时，辐射噪声为91.1 dB.

(a) 500 Hz

(b) 1 000 Hz

图9 齿轮箱外声场网格

4.3 齿轮箱振动响应计算结果

采用齿轮箱声振耦合分析模型计算声学量的同时，也可获得结构的振动响应.图11给出了500 Hz,1 000 Hz时齿轮箱表面的振动速度云图.由图可知，当频率为500 Hz时，齿轮箱表面最大振动速度幅值为10.6 mm/s，出现在齿轮箱的顶部.

5 齿轮箱振动噪声试验

为验证仿真结果的准确性，在重庆齿轮箱有限责任公司的协助下，搭建了如图12所示的船用齿轮箱振动噪声试验平台.测试工况与仿真分析一致，即输入转速为750 r/min，输出功率为400 kW.

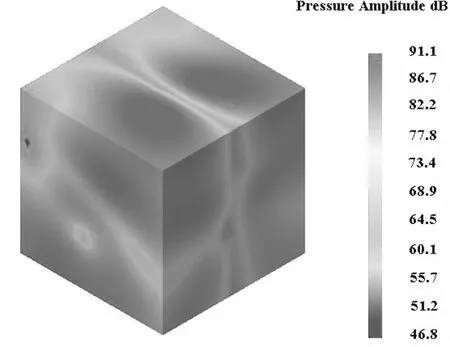
(a) 500 Hz

(b) 1000 Hz

(a) 500 Hz

(b) 1000 Hz

齿轮箱振动响应测点布置见图4.将加速度传感器测得的振动加速度信号经电荷放大器放大后，由智能信号采集处理分析仪进行采集，最后利用DASP软件进行数据处理，得到安装支座处各测点的垂向振动加速度均方根值，如表4所示.对比表3给出的仿真结果，两者的最大相对误差为12.8%.

图12 船用齿轮箱振动噪声试验平台

表4 垂向振动加速度实测值

图13给出了测点1的垂向振动加速度实测曲线.由图可知，振动加速度的峰值频率出现在25 Hz,229.69 Hz,525 Hz和570 Hz处，分别对应输入轴转频的2倍频、输出级齿轮副的啮合频率、输入级齿轮副的啮合频率及其边频，最大峰值频率出现在啮合频率附近.由于齿轮副存在加工误差和传动误差，齿轮啮合频率及其高次谐波两侧出现边频带，边频间隔为齿轮的转频，形成齿轮啮合频率的调制.

时间t/s(a) 时域曲线

频率f/Hz(b) 频域曲线

图14给出了齿轮箱输出端场点的A计权倍频程辐射噪声实测与仿真结果的对比曲线，两者吻合较为良好.

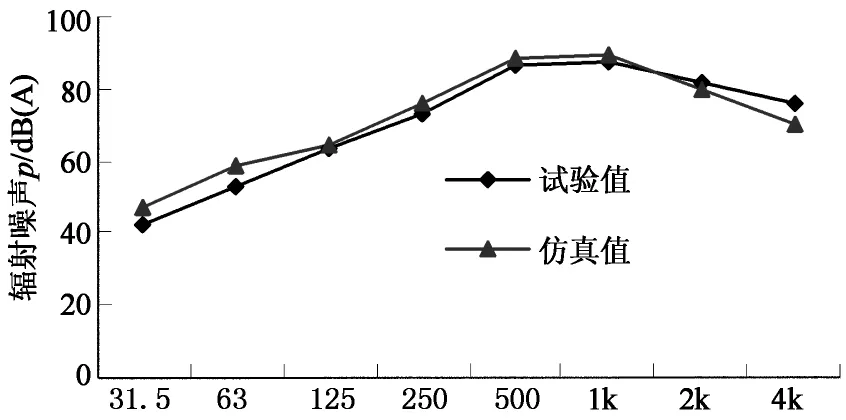
频率f/Hz

6 结 论

1) 综合考虑齿轮副时变啮合刚度、齿侧间隙、轴承支撑刚度等内部激励以及螺旋桨外部激励，建立了含传动系统及结构系统的船用齿轮装置多刚体系统动力学模型，计算了齿轮副动态啮合力及轴承支反力.

2) 建立了船用齿轮箱多柔体系统动力学模型，采用模态叠加法计算了箱体表面的动态响应，其峰值频率均出现在齿轮副啮合频率及其倍频处.

3) 建立了船用齿轮箱声振耦合分析模型，预估了齿轮箱表面声压及外声场辐射噪声，与齿轮箱振动噪声试验台架实测结果对比，两者吻合良好.

[1] 陈学森, 董海军, 刘晓宁. 含时变啮合刚度的间隙非线性齿轮系统的混沌控制[J]. 机械科学与技术, 2006, 25(9): 1035-1037.

CHEN Xue-sen, DONG Hai-jun, LIU Xiao-ning. Chaos control of a nonlinear gear system with clearance and time-varying stiffness[J]. Mechanical Science and Technology, 2006, 25(9): 1035-1037.(In Chinese)

[2] FERNANDEZ A, IGLESIAS M, DE-JUAN A,etal. Gear transmission dynamic: Effects of tooth profile deviations and support flexibility [J]. Applied Acoustics, 2014, 77(3): 138-149.

[3] WANG J, LIM T C, LI M F. Dynamics of a hypoid gear pair considering the effects of time-varying mesh parameters and backlash nonlinearity[J]. Journal of Sound and Vibration, 2007, 308(1/2): 302-329.

[4] MORADI H, SALARIEH H. Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity[J]. Mechanism and Machine Theory, 2012, 51(5): 14-31.

[5] BYRTUS M, ZEMAN V. On modeling and vibration of gear drives influenced by nonlinear couplings[J]. Mechanism and Machine Theory, 2011, 46(3): 375-397.

[6] GUO Y, PARKER R G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity[J]. European Journal of Mechanics, 2010, 29(6): 1022-1033.

[7] BAGUET S, JACQUENOT G. Nonlinear couplings in a gear-shaft-bearing system[J]. Mechanism and Machine Theory, 2010, 45(12): 1777-1796.

[8] 林腾蛟, 廖勇军, 李润方, 等. 双环减速器辐射噪声数值仿真及试验研究[J]. 振动与冲击, 2010, 29(3): 43-47, 203.

LIN Teng-jiao, LIAO Yong-jun, LI Run-fang,etal. Numerical simulation and experimental study on radiation noise of double-ring gear reducer[J]. Journal of Vibration and Shock, 2010, 29(3): 43-47, 203. (In Chinese)

[9] LIN Teng-jiao, HE Ze-yin, GENG Fei-yu,etal. Prediction and experimental study on structure and radiation noise of subway gearbox [J]. Journal of Vibroengineering, 2013, 15(4): 1838-1846.

[10]ABBES M S, BOUAZIZ S, CHAARI F,etal. An acoustic structural interaction modelling for the evaluation of a gearbox-radiated noise[J]. International Journal of Mechanical Sciences, 2008, 50(3): 569-577.

[11]YUKSEL E, KAMCI G, BASDOGAN I. Vibro-acoustic design optimization study to improve the sound pressure level inside the passenger cabin[J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2012, 134(6): 1-9.

[12]汪怡平, 谷正气, 杨雪, 等. 汽车空调出风管道气动噪声分析与控制[J]. 湖南大学学报:自然科学版, 2010, 37(3): 24-28.

WANG Yi-ping, GU Zheng-qi, YANG Xue,etal. Study of the fatigue strength of the dynamic meshing of the spiral bevel gears of reducer[J]. Journal of Hunan University :Natural Sciences, 2010, 37(3): 24-28. (In Chinese)

Multi-body Dynamic Simulation and Vibro-acoustic Coupling Analysis of Marine Gearbox

LIN Teng-jiao1†, HE Ze-yin1, ZHONG Sheng1, LIU Wen1, LV He-sheng2

(1. The State Key Laboratory of Mechanical Transmission, Chongqing Univ, Chongqing 400044, China；2. Chongqing Gearbox Co Ltd, Chongqing 402263, China)

Based on the dynamic theory of multi-body system, a multi-rigid-body dynamic model, which contains the transmission system and structure system of marine gear device, was established by taking account of the internal excitations such as the time-varying mesh stiffness, tooth backlash and bearing stiffness and the external torque excitation caused by the propeller. Then, the dynamic meshing forces of gear pairs and bearing reaction forces were calculated. Using the modal superposition method, the dynamic response of housing surface was solved after the multi-flexible-body dynamic model was developed on the basis of the flexible gearbox and pedestal. Afterwards, a strongly vibro-acoustic coupled model of this gearbox was built by employing the frequency histories of bearing reaction forces obtained from the multi-body dynamics analysis, and the surface sound pressure of gearbox and the radiation noise of outer sound field were calculated. The results show that the peaks of dynamic meshing forces, reaction forces of bearings and dynamic responses of gearbox appear at the position of mesh frequency and its multiples of gear pairs, and the simulation results of vibration acceleration of gearbox and the radiation noise of outer sound field are in good agreement with the experiment results measured in the vibration and noise test platform of the gearbox.

gearbox; multi-body dynamics; vibro-acoustic coupling; dynamic response; radiation noise

1674-2974(2015)02-0022-07

2014-02-24

国家自然科学基金资助项目(51175524),National Natural Science Foundation of China(51175524)；重庆市自然科学基金计划资助项目(cstcjjA70002)

林腾蛟(1968-)，男，浙江宁波人，重庆大学教授，博士†通讯联系人，E-mail:tjlin1968@126.com

TH132.41

A