基于正交设计与主成分回归的矿柱稳定性分析

罗周全，彭 东，苏汉语，王婷玉

(中南大学资源与安全工程学院，湖南长沙 410083)

0 引言

在长时间、大范围的地下开采过程中，大量的采空区是危及矿山安全生产的主要原因之一，而矿柱又是影响采空区稳定性的主要结构单元。矿柱的失稳将导致空区顶板大面积坍塌，造成大量的人员伤亡和严重的财产损失［1］。因此，加深对矿柱稳定性研究对实现地下矿山高效、安全回采具有重要意义。

目前许多专家学者对矿柱稳定性进行了研究。郑泽岱和刘沐宇等分析得出了矿柱安全系数的点安全系数计算方法［2］;赵奎和万林海等提出了基于声波测试的模糊推理系统［3］;王学滨利用FLAC对屈服矿柱渐进破坏及应力分布数值模拟［4］;尹升华、李坚玲等通过正交极差分析方法对矿柱稳定性影响因素的敏感性进行了分析［5-8］。这些方法虽然能实现矿柱稳定分析，但存在以下两个缺陷:①分析过程复杂，分析结果不能直观、全面的反映总体信息指标;②没有考虑各个影响因素之间的交互作用，分析结果存在一定误差。

本文在分析矿柱稳定性影响因素敏感性时，将正交设计极差分析结果与考虑了各影响因素交互作用的主成分回归分析结果进行比较，充分证明了主成分回归分析方法在对重要度排序方面更具有优越性。另外，通过主成分相关系数等分析结果以及稳定性系数与各个影响因素之间的线性回归模型，可以定量的得到各影响因素之间，以及各影响因素与矿柱稳定性之间的关系，使得分析结果得到最优化处理。

1 基于正交设计的主成分回归分析

1.1 点安全系数计算法

本文根据郑泽岱和刘沐宇等提出的矿柱点安全系数计算方法，得出了矿柱稳定性安全系数表达式。该方法既考虑了矿柱各点的实际应力状态，又包含了强度破坏准则的内容，在计算矿柱稳定性系数上得到广泛应用。

点安全系数计算方法主要考虑8项影响因素:⑴采深(H);⑵矿房宽度(Wo);⑶矿柱宽度(WP);⑷矿柱高度(h);⑸矿体的单轴抗压强度(σc);⑹上覆岩层容重(γ);⑺矿柱长度(Lp);⑻ 矿柱长度方向的间距(Lo)。

计算矩形矿柱安全系数的基本公式为

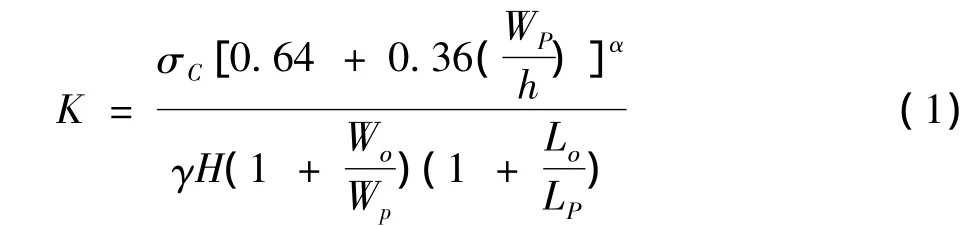
当矿柱的形状为方形时，矿柱长度与矿柱宽度相同，矿柱长度方向的间距与矿房宽度相同，于是，计算方形矿柱安全系数的公式可简化为

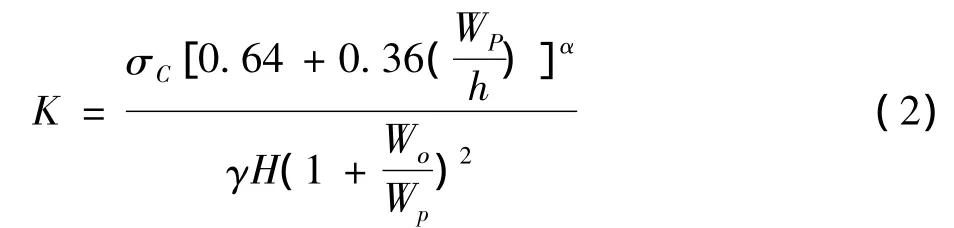
本文主要就矿柱是方形的这种情况进行讨论分析。

1.2 正交设计的实验方法原理

正交设计是研究多因素多水平，根据正交表设计实验的分析方法。本文主要根据点安全系数计算公式得出各因素在不同水平状态下的矿柱稳定性系数并建立正交设计表。根据各因子在同一水平的平均实验指标Kij，从而得到主成分分析的数据矩阵［9］。

式中:r——因素j在i水平下的实验次数;

Xijk——因素j在第i水平下第k次实验的结果指标值;

Kij——因素j在i水平下的平均实验指标。

另外，计算各列的极差R。根据极差大小，可确定各因素重要度顺序［10］。

1.3 主成分回归分析原理

主成分回归分析的原理是用主成分分析提取的主成分与因变量建立回归模型［11］。由于主成分分析可以很好的解决回归分析中的多重共线性问题，而且各主成分之间不相关［12］。因此，能更加全面、具体的反映各相关因素之间的综合信息。

1.4 主要分析步骤

(1)正交设计实验获得各因子在同一水平的平均实验指标Kij，作为主成分分析的数据矩阵。

(2)对各个因素构成的数据表做主成分分析。根据选定的累积贡献率，选取前n个主成分。并根据主成分因子负荷矩阵的结果，可获得各主成分F与各影响因素之间的线性关系，即:

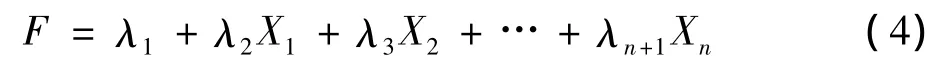
(3)将前n个主成分F作为自变量，作多元线性回归。得到各主成分F与因变量Y之间的线性关系，即:

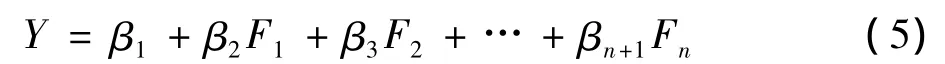
(4)由于每个主成分F均是N个因素X作为自变量的线性组合，因此，经最终转化，可获得线性回归模型，即:

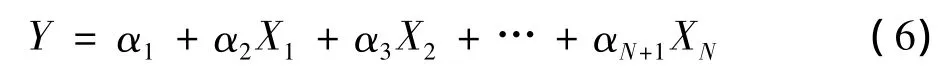
2 应用实例

2.1 正交设计分析

某地下大型铜矿从投产主要采用阶段崩落法进行开采。但是，地表已经出现大量的坍塌坑和采空区群，给生产安全留下了重大隐患［13］。根据该矿的采矿工艺与赋存条件等要求，将矿柱稳定性的6个影响因素划分为5个水平［14］(表1)。考虑到有6个因素，5个水平，选用L25(56)正交表。按式(3)计算矿柱安全系数。实验方案及分析结果见表2。

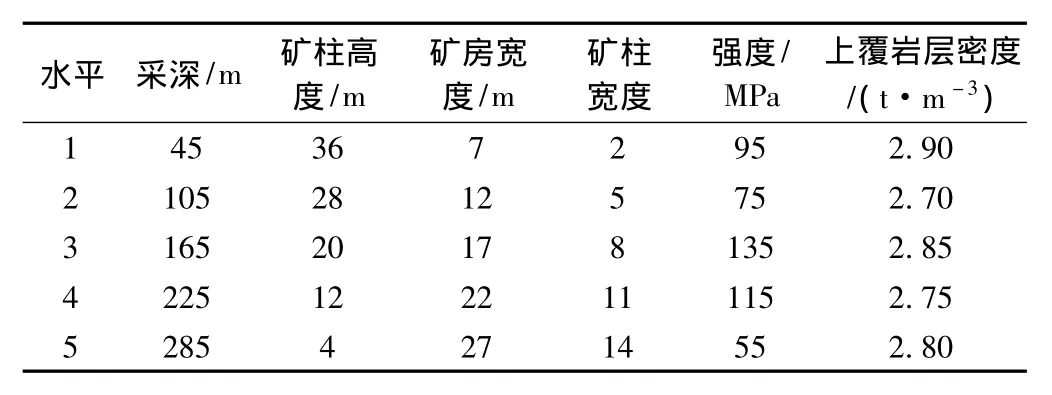
表1 实验因素水平划分方案Table 1 The level division scheme of experimental factors

表2 矿柱稳定性正交设计方案及分析结果Table 2 Orthogonal design of pillar stability and result analysis

根据正交极差分析结果可知，矿柱稳定性影响因素的主次顺序为:采深H＞矿柱高度h＞矿柱宽度WP＞矿房宽度Wo＞上覆岩层密度γ＞矿体矿压强度σ。

采深、矿房宽度与矿柱稳定性影响因素呈负相关，其他四个方面都与矿柱稳定性系数呈正相关。其中，矿柱宽度、采深与矿柱稳定性系数关系(图1、图2)。

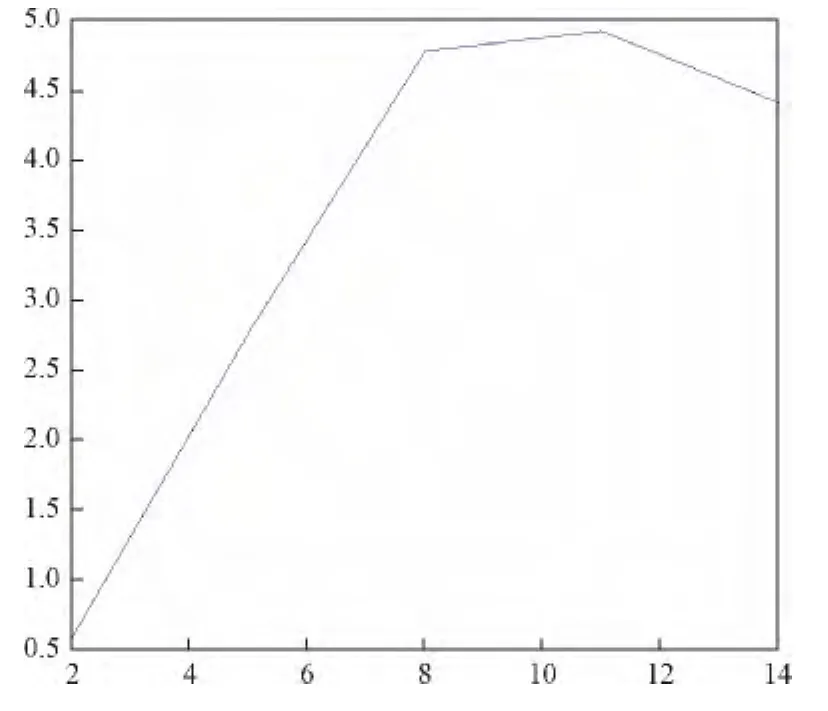
图1 矿柱宽度与矿柱稳定性系数关系Fig．1 The relationship between the width of the pillar and the pillar stability coefficient

图2 采深与矿柱稳定性系数之间的关系Fig．2 The relationship between the deep mining and pillar stability coefficient

2.2 主成分分析

由上述正交分析结果可得各影响因素稳定性系数均值结果见表3。

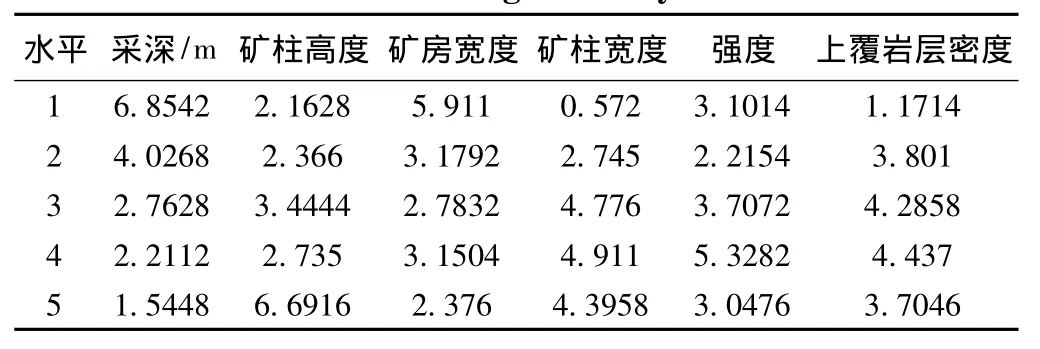
表3 稳定性系数均值Table 3 The average stability coefficient

由稳定性系数均值分析结果可得主成分分析的数据矩阵，即:

进行主成分分析，结果见表4～表6。

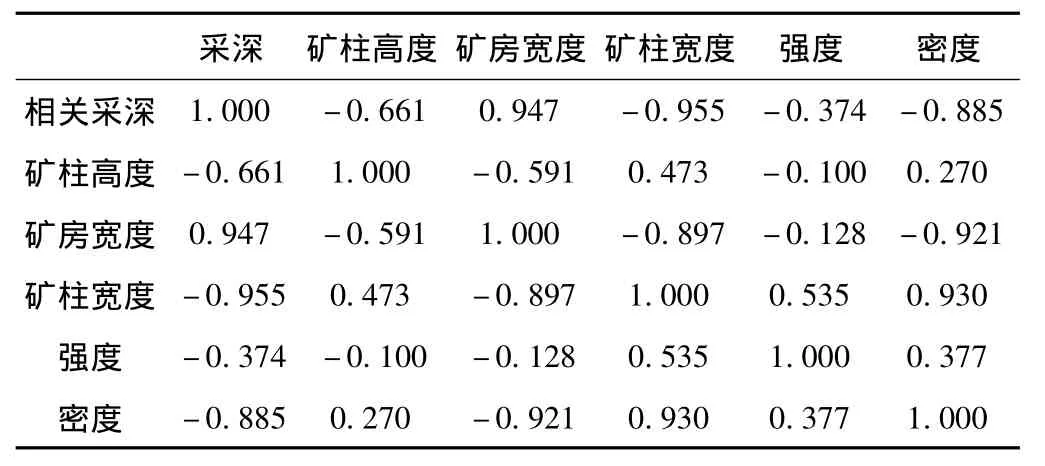
表4 相关系数矩阵Table 4 Correlation matrix

表5 主成分特征值及贡献率Table 5 Principal component eigenvalues and contribution rate

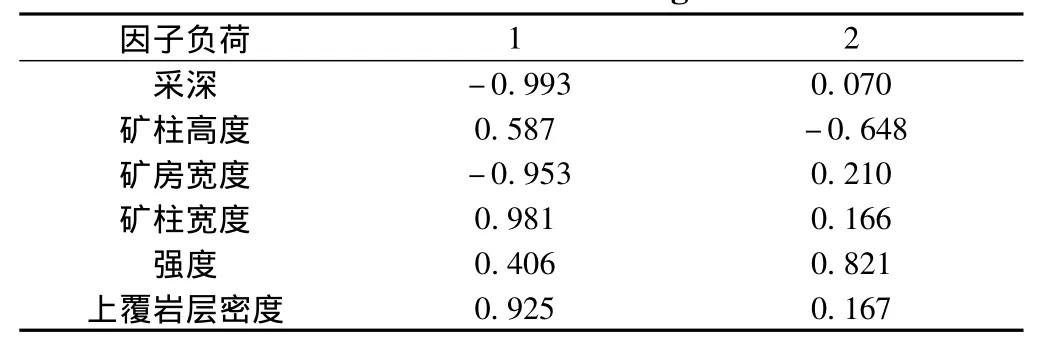
表6 因子负荷矩阵Table 6 The factor loading matrix

由表4分析结果可知采深与矿房宽度、矿柱宽度、密度具有很强的相关性，另外密度与矿房宽度、矿柱宽度也具有很强的相关性。因此，在分析各个影响因素重要性顺序的时候，应该考虑各影响因素之间的交互作用。

由表5主成分分析特征值与贡献率可知，第一、二主成分的贡献率累积已达到90.330%。由表6的分析结果可得，两个主成分的线性表达式为

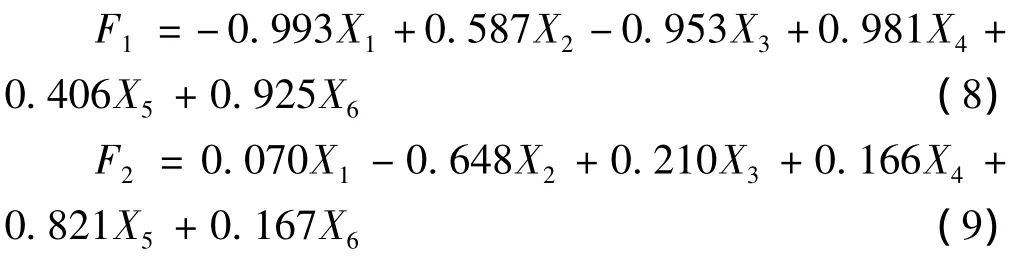
由上式分析结果可知，主成分F1主要反映采深、矿房宽度、矿柱宽度与上覆岩层密度的信息，主成分F2主要反映矿柱高度与抗压强度的信息。

2.3 回归分析

由上表4相关系数矩阵的结果可知，各自变量之间均在很强的相关性，因此，可以合理的建立因变量与自变量之间的线性模型。但由于自变量个数较多，这样在建立线性模型时，可能会出现多重共线性问题［14］。因此，应该先进行共线性诊断，各诊断指标的结果数据见表7。

表7 共线性诊断指标Table 7 Collinearity diagnosis index

从上述共线性诊断的特征值结果可以得出，除了维度1之外，其他的都接近于0，说明该模型存在严重的线性关系。另外，条件索引第6、7列均大于10，说明可能存在较严重的线性关系。而且，方差比例内存在1的数，也可以说明存在严重的线性关系。

将矿柱稳定性系数作为因变量，两个主成分作为自变量，作多元线性逐步回归，分析结果见表8～9。

由表9可知，Sig小于0.01，说明回归方程的线性关系非常显著。故建立的主成分线性关系方程为:

表8 回归分析的显著性检验Table 8 Significant test of regression analysis

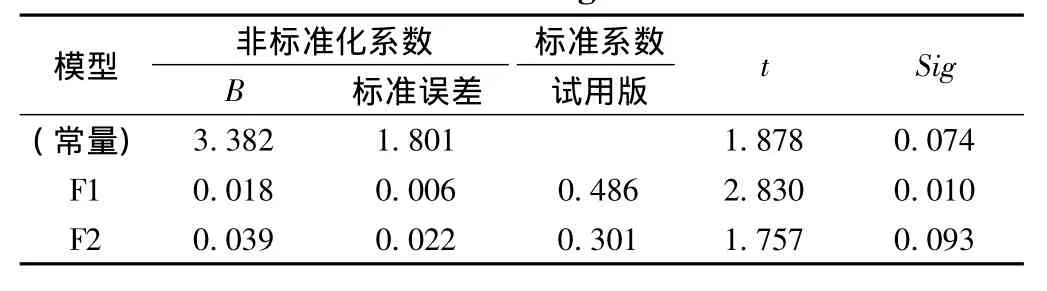
表9 标化后回归系数Table 9 Standardized regression coefficient

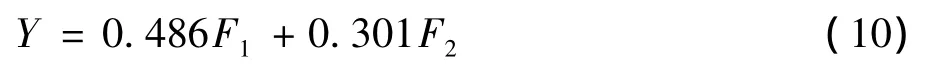
因此最终回归模型为:

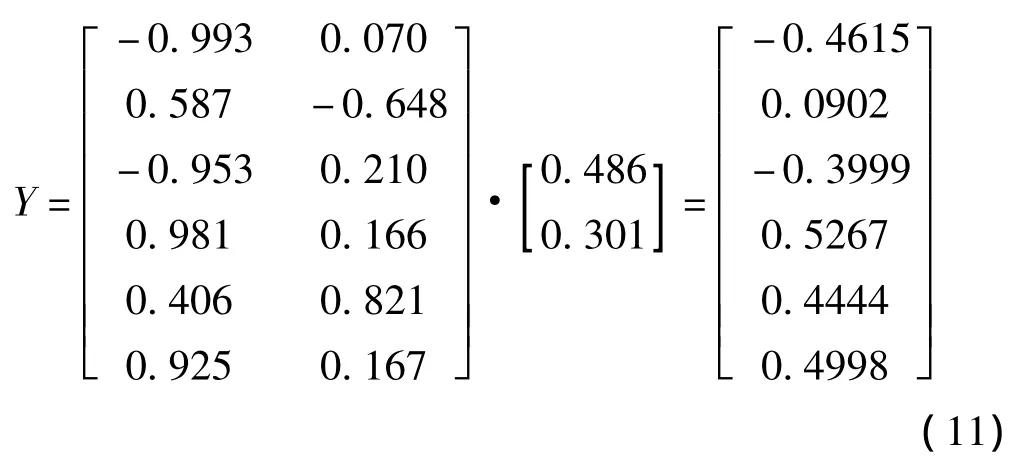
由此，可得出各影响因素作为自变量，矿柱稳定性系数作为因变量的最终线性回归模型，即:

3 结论

(1)从最终主成分回归方程可以看出，采深与矿房宽度对矿柱稳定性系数起反作用，其他四个因素都起促进作用。

(2)由线性回归模型系数可知，矿柱宽度与上覆岩层密度对矿柱稳定性影响程度最大，这两方面每提高1%，将导致稳定性系数增加0.5%左右。采深、单轴抗压强度与矿房宽度对矿柱稳定性影响较大，这三方面每提高1%。将导致稳定性系数发生0.4%左右的变化。另外可知，矿柱高度对稳定性系数的影响最小。

(3)由相关系数矩阵与共线性诊断指标可知，矿柱稳定性各影响因素之间具有极强的相关性，在进行敏感度分析是应该考虑交互作用。

(4)通过上述回归方程获得各影响因素敏感度分析结果，即为:矿柱宽度WP＞上覆岩层密度γ＞采深H＞单轴抗压强度σc＞矿房宽度Wo＞矿柱高度h。与上述极差分析结果比较可知，基于正交设计与主成分回归分析方法在分析各影响因素敏感度更准确。

［1］王国焘，罗周全，刘晓明，等.金属矿采空区三维探测及可视化建模与应用［J］.中国地质灾害与防治学报，2010，21(1):104-109.WANG Guotao，LUO Zhouquan，LIU Xiaoming，et al.Application of 3D monitoring and visual modeling cavities in metallic mines based on cavity features［J］.The Chinese Journal of Geological Hazard and Control，2010，21(1):104-109.

［2］郑泽岱，刘沐宇，祝文化.计算矿柱安全系数的新方法［J］.化工矿山技术，1994，23(3):16-19.ZHANG Zedai，LIU Muning，ZHU Wenhua.A new method for calculation of safety factor of one pillars［J］.Chemical Mining Technology，1994，23(3):16-19.

［3］赵奎，万林海，饶运章，等.基于声波测试的矿柱稳定性模糊推理系统及其应用［J］.岩石力学与工程学报，2004，23(11):1804-1809.ZHAO Kui，WAN Linhai，RAO Yunzhang，et al.Fully reasoning system pillar stability based on sonic wave measurement and it’s application［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(11):1804-1809.

［4］王学滨.屈服矿柱渐进破坏及应力分布数值模拟［J］.中国地质灾害与防治学报，2006，17(2):50-56.WANG Xuebin.Numerical simulation of progressive failure and stress distribution of yield pillars［J］.The Chinese Journal of Geological Hazard and Control.2006，17(2):50-56

［5］尹升华，吴爱祥，李希雯.矿柱稳定性影响因素敏感性正交极差分析［J］.煤炭学报，2012，37:48-52.YIN Shenghua，WU Aixiang，LI Xiwen.Orthogonal polar difference analysis for sensitivity of the factors influencing the ore pillar stability［J］.Journal of China Coal Society，2012，37:48-52.

［6］宋卫东，曹帅，等.矿柱稳定性影响因素敏感性分析及其应用研究［J］.岩土力学，2014，35(1):271-277.SONG Weidong，CAO Shuai，et al.Sensitivity analysis of impact factors of pillar stability and its application［J］.Rock and Soil Mechanics，2014，35(1):271-277.

［7］李坚玲.全面法采场矿柱稳定性及影响因素敏感性分析［J］.有色金属，2010，62(5):6-8.LI Jianling.Stope Pillarstability and sensitivity analysis of effect factors in overall mining method［J］.Nonferrous Metals，2010，62(5):6-8.

［8］党洁，张晨洁，郭生茂，等.隔离矿柱回采稳定性影响因素的正交试验分析［J］.金属矿山，2014(5):24-26.DANG Jie，ZHANG Chenjie，GUO Shengmao，et al.Orthogonal tests analysis on the influencing factors for the stoping stability of isolated pillars［J］.Metal Mine，2014(5):24-26.

［9］XIN Chaozhao，WEN Qiaolin，QING Fuzhang.Enhanced particle swarm optimization based on principal component analysis and line search［J］.Applied Mathematics and Computation，2013，(72).

［10］余能，刘正宇，胡培良，等.边坡稳定性影响因素的敏感性正交极差分析［J］.矿业研究与开发，2013，33(5):66-69.YU Neng ，LIU Zhengyu ，HU Peiliang，et al.Orthogonal experiment rang analysis of sensitivity of factors influencing slope stability［J］.Mining R＆D，2013，33(5):66-69.

［11］李毛侠.安徽省消费需求影响因素的主成分回归分析［J］.现代物业，2010，9(2):48-51.LI Maoxiao.Effect of Anhui province consumer demand in principal component regression analysis［J］.Modern property，2010，9(2):48-51.

［12］蔡善荣，阮红芳，等.以主成分回归分析方法探讨人均卫生费用影响因素的研究［J］中国卫生事业管理，2001(7):399-400 CAI Shanrong ，YUAN Hongfang，et al.The principal component regression analysis of the factors influencing the per capita health expenditure method［J］Chinese Health Cause Management，2001(7):399-400.

［13］胡永泉，张传信，匡玉生，等.冬瓜山铜矿西山采空区治理工程研究与实践［J］.金属矿山，2011(5):23-27.HU Yongquan，ZHANG Chuanxin，KUANG Yusheng，et al.Research of treatment engineering of Xishan mined-out area in Dong gua shan copper mine and its practice［J］，Metal Mine，2011(5):23-27.

［14］崔希民，左红飞，王金安.急倾斜煤层开采地表塌陷坑形成机理与安全矿柱尺寸研究［J］.中国地质灾害与防 治学报，2000，11(2):67-69.CUI Ximin，ZUO Hongfei，WANG Jinan.Discussion on mechanism of surface collapse pit and dimensions of obstructive ridge for steep inclined coal seam mining［J］.The Chinese Journal of Geological Hazard and Control，2000，11(2):67-69.