不同截面形式简支梁计算模态分析

高 冉 苏义坤 李熠诗

(东北林业大学，黑龙江 哈尔滨 150040)

φ=ω2φ



不同截面形式简支梁计算模态分析

高 冉 苏义坤 李熠诗

(东北林业大学，黑龙江 哈尔滨 150040)

为了探究不同截面形式下简支梁的动力特性差异，利用有限元计算软件Ansys12.1对矩形、圆形、工字形以及空心四种截面的简支梁进行计算模态分析，结果表明圆形截面的模态自振频率要比其他截面高，在前四阶模态中主要出现的变化是横弯变形以及竖弯变形。

简支梁，横截面，模态分析

1 概述

模态分析是研究结构动力响应的基础，模态为结构的固有动力特性，每个模态都具有特定的频率、周期、阻尼比、振型等模态动力参数。这些模态动力参数可以通过现场试验实测得到，也可以通过有限元软件计算得到，计算模态分析源于振动原理，单自由度的结构是最基本的计算系统，在实际结构中通常是多自由度结构，但是对于单自由度结构计算可以得到很多基本的动力特性参数，因此多自由度结构通常可以看成是多个单自由度结构的叠加。

计算模态分析的基本原理就是将线性定常系统振动微分方程组中的物理坐标变换为模态坐标解耦方程组，将其变换为一组以模态坐标及模态参数描述的独立方程，以此得出系统的模态参数。

计算模态分析的思路是将多自由度结构体系转化的单自由度结构体系的叠合称之，多自由度结构体系的自振动力微分方程如式(1)所示：

(1)

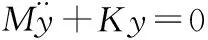
(2)

对式(2)中的矩阵方程进行转化，可以得到计算简支梁结构自振频率的矩阵方程式如式(3)所示。

φ=ω2φ

(3)

其中，φ为结构振型向量；ω为自振频率。因此可以通过计算模态分析的方法来分析简支梁结构的动力特性以及结构在某一受影响的外界频率范围内的模态特点，以此来预测结构在空间中不同振源作用下产生的实际动力响应。因此模态分析是了解结构动力特性并以此分析结构动力响应的重要方法。

2 计算模型

在计算模态分析中，建立合适准确的有限元模型是最为基础也是最为关键的一步。本文通过大型有限元计算软件Ansys12建立简支梁的三维有限元模型，简支梁梁长10 m。模型采用材料库的Beam188单元实现，通过截面赋予的方式自上而下进行建模，简支梁赋予四种截面形式，分别是实心矩形、圆形、工字形以及空心矩形，其中实心矩形、空心矩形以及工字形截面的梁高为1 m，梁宽为0.5 m，圆形截面的径长为1 m。建立好有限元模型以后划分网格并对支点进行简支梁约束，并对梁体施加自重荷载，有限元建立的不同截面的三维模型如图1所示。

3 模态分析

建立好有限元模型以后就需要提取结构模态进行求解。在有限元软件Ansys中提供了多种提取结构模态的办法：分块 Lanczos 法、Subspace子空间法、PowerDynamics法、非对称法、阻尼法以及缩减法等等。本次模态使用Subspace子空间法提取了不同截面简支梁的前10阶模态，得到了前10阶模态的自振频率、自振周期以及模态振型等动力特性参数，其中不同截面简支梁前10阶模态的自振频率对比如图2所示。而将不同截面简支梁前5阶模态的振型特点列于表1。

如图2所示，四种截面的简支梁的自振频率随着模态阶数的增大而有所增加，而且增大的幅度是递增的，增长的趋势很相近都是指数型增长，但在第10阶模态时四种截面的自振频率基本相同。同时从图中可以看出，在10阶以前的自振频率相差还是较大的，其中圆形截面简支梁在每阶模态的自振频率都要比其他三个大，其次是空心矩形，然后是实心矩形，最后是工字形截面。因此在所有的截面中，工字形截面在振动前期最易发生共振，根据式(3)的表述，由于简支梁的阻尼条件均一致，改变了截面形状，进而导致了梁体的刚度矩阵以及梁体的质量矩阵发生了改变，其中的增大会导致结构自振频率的增大，而的增大则会使得自振频率减小，因此工字形截面的简支梁由于其横向抗弯刚度以及抗扭刚度较小而使得其自振频率最低，而由于实心矩形的重量要大于空心矩形，所以其实心矩形简支梁的自振频率要比空心矩形简支梁的自振频率小，而圆形截面由于各向刚度较好而质量相对较小导致不易自振。

表1 人行钢桥自振频率及振型特点

由表1可以看出，四种截面简支梁的振型变化都是由低阶振型向高阶振型变化。对于实心矩形简支梁在前5阶模态分析中主要出现的振型特点是竖弯以及横弯，这与空心矩形截面简支梁较为类似，但是由于空心矩形简支梁的质量较轻，因此在前5阶模态中仅出现了二阶横弯的变形，而实心矩形简支梁则出现了三阶横弯的振型特征。对于圆形截面，其首先出现的竖弯变形，且由于其抗弯刚度较大，在前5阶模态中并未出现二阶弯曲变形，但是由于其抗扭惯性矩较小，因此抗扭刚度要比矩形截面小，因此在第5阶模态中出现了扭转变形。工字形截面的简支梁由于其横向抗弯刚度较小，因此在前5阶模态中有四个模态出现了横弯的振型特征。

4 结语

通过计算模态分析是可以得到不同截面的简支梁的动力特性。其中前10阶模态分析中圆形截面简支梁在每阶模态的自振频率都要比其他三个大，其次是空心矩形，然后是实心矩形，最后是工字形截面，到第10阶模态时四种截面的自振频率基本相同。实心矩形截面简支梁与空心矩阵简支梁在前5阶模态分析中主要出现的振型特点是竖弯以及横弯，因此在进行抗震设计时可以加强抗弯设计，工字梁最易发生振动，特别是当跨径较大时，需要加强其抗横弯变形能力，圆形截面简支梁抗弯性能较好，但最易出现扭转振型，需要在抗震设计时注意。

[1]傅志方.模态分析理论与应用.上海：上海交通大学出版社，2000.

[2]李廉锟.结构力学.北京：高等教育出版社，2010.

[3]何钰龙,李 超,申杨凡,等.人行钢桁架桥动力特性及反应谱分析.黑龙江工程学院学报，2015，29(1):12-15.

[4]王 洋，郝志军.ANSYS在土木工程应用实例.北京：中国水利水电出版社,2010.

Computational modal analysis with different cross-section beam

Gao Ran Su Yikun Li Yishi

(NorthestUniversityCollege,Harbin150040,China)

In order to explore the different dynamic characteristics between different section forms of beam, using the finite element modal analysis calculation software Ansys12.1 for rectangular, round, and four kinds of hollow I-shaped section beam, results show that the modal frequencies of circular cross section than the cross section of his high, changes occurred mainly in the first four modes in the main is the transverse bending deformation and bending deformation.

beam, cross section, modal analysis

1009-6825(2015)18-0040-02

2015-04-13

高 冉(1992- )，男，在读本科生； 苏义坤(1972- )，男，博士，教授； 李熠诗(1994- )，女，在读本科生

U442

A