椭圆抛物体形微凸体弹性接触力学模型
2015-03-07刘伟强张进华洪军朱林波
刘伟强,张进华,洪军,朱林波
(西安交通大学机械制造系统工程国家重点实验室, 710049, 西安)
椭圆抛物体形微凸体弹性接触力学模型
刘伟强,张进华,洪军,朱林波
(西安交通大学机械制造系统工程国家重点实验室, 710049, 西安)
为了更准确地描述粗糙结合面的微观接触特性,构建了一种椭圆抛物体形微凸体曲面弹性接触模型。该模型同时考虑了微凸体正接触与侧接触的情形,采用了Weingarten映射的方法来求解接触点处的曲率,并结合赫兹曲面接触理论进行求解,得出椭圆抛物体在弹性侧接触时的接触面积与接触位移的解析公式。讨论了微凸体在不同相对位置下及不同椭圆率的情况下接触面积与接触位移的变化,并通过有限元仿真与该模型进行了对比计算,结果表明:椭圆率对接触面积、接触位移的计算结果影响较大,当椭圆率在超过0.9后,两微凸体接触面积迅速减小,接触位移迅速增大;提出的模型与有限元模型结果相比,两微凸体接触位移计算结果差异最大为10%,接触面积结果差异最大为6.2%。该模型同样适用于求解几何模型具有二阶连续偏导数的微凸体弹性接触问题,为研究形状更为复杂的微凸体接触奠定了基础。
赫兹曲面接触;微凸体;弹性接触
机械结合面的接触刚度、接触面积等对机械系统的动静态特性、热电传导特性有着重要的影响。为了更准确地预测结合面宏观动静态接触特性,学者们充分研究了机械结合面微观接触原理,提出了许多微凸体接触解析模型。文献[1]假设机械结合面上分布着球形微凸体,并且微凸体高度呈高斯分布,最后得出了经典的Greenwood-Williamson(GW)模型。在GW模型的基础上发展了许多考虑塑性变形的微凸体接触模型[2-3],微凸体高度分布也从GW模型的高斯分布扩展到了非高斯分布[4-6]。除假设微凸体形状为球形外,许多学者将微凸体的形状扩展到了非球状[7-9]。文献[7]研究了椭圆抛物体形微凸体正接触的力学模型;文献[10-11]研究了旋转抛物体形微凸体正、侧接触时的接触变形的问题。在旋转抛物体形微凸体的基础上,文献[11]采用分水岭算法,将结合面划分成单个微凸体,成功地将微凸体的模型应用到结合面接触刚度的计算中。
上述模型大部分以微凸体的峰顶法向接触模型为主,微凸体的变形大都是峰对峰的正接触变形。基于微凸体形状为球形及旋转抛物体形的接触理论,可以推出单对微凸体正接触时的接触面为圆形,与实际情况不符[12]。造成这种差异的原因是微凸体本身形状并非是完全轴对称,并且微凸体往往难以恰好发生峰对峰的正接触。同样,现有的椭圆抛物体形微凸体接触模型也只考虑了法向正接触情形[13]。
实际中,两个微凸体接触往往难以保证严格对中,从而形成侧接触状态。文献[10-11,14]研究了抛物体状的微凸体侧接触的力学模型,但微凸体接触点处曲率等相关参数是由抛物体的二维截面计算得来,由于曲面曲率与曲线曲率有着本质的区别,两者不能互换,因此文献[10-11,14]的模型在计算真实机械结合面微凸体接触问题时,存在着一定的理论缺陷。
基于以上研究现状,为解决机械结合面法向、切向接触参数计算等问题,本文提出了以椭圆抛物体状微凸体来代替现有球形微凸体的弹性接触模型。该模型同时考虑了微凸体正接触与侧接触的情形,采用了Weingarten映射的方法来求解接触点处的曲率,结合赫兹曲面接触理论进行求解,得出椭圆抛物体在弹性侧接触时的接触面积与接触位移的解析公式。同时,讨论了微凸体在不同位置及不同椭圆率的情况下接触面积与接触位移的变化,并通过有限元仿真对本文模型进行了对比。本文模型结合分水岭法[11]可将结合面的表面划分成单个的微凸体并将其拟合成椭圆抛物体,最终可实现结合面法向及切向接触刚度、阻尼等接触参数计算[11]。
1 力学模型的构建
1.1 模型基本假设
(1)机械结合面表面微凸体形状可由椭圆抛物体表征。椭圆抛物体的表达式为
(1)
式中:a、b、c为微凸体的形状参数;θ、rx、ry为微凸体表面形状的位置参数。
(2)微凸体的接触为曲面接触,微凸体不仅会产生峰对峰的正接触,也会产生侧接触。
(3)微凸体的材料属性为各向同性,为了简化模型,不考虑材料的塑性变形,不考虑摩擦。
(4)微凸体接触受力遵循Hertz曲面接触理论的一般情形。
1.2 椭圆抛物体接触几何模型
1.2.1 椭圆抛物体几何模型 假设分布于粗糙结合面上的微凸体为椭圆抛物体,如图1所示。为了便于分析微凸体侧接触对接触面积及接触位移的影响,假定下微凸体椭圆面的中心为坐标原点所在的位置,上微凸体相对于下微凸体的相对位置关系以两微凸体中心线在x、y方向的偏移与两微凸体长半轴间的夹角α表示。两椭圆抛物体方程如下
(2)
式中:z1、z2分别表示下微凸体与上微凸体表面形状;夹角α表示上微凸体z2与下微凸体z1长半轴之间的夹角;dx、dy表示上微凸体z2中心线相对于下微凸体z1中心线的偏移。

图1 椭圆抛物体接触模型
1.2.2 接触点坐标及接触方位求解 为研究椭圆抛物体的正、侧接触,首先需要求出两微凸体在任意相对位置下的接触点坐标(xc,yc)。椭圆抛物形微凸体两表面的接触间距为
(3)
接触点(xc,yc)需满足的条件为:(xc,yc)为接触间距的极小值点,z(x,y)对xc、yc的偏导为0;接触间距d不大于0。因此,接触点处的判别式为
(4)
给定两微凸体的表达式,即可求得接触点(xc,yc)的准确位置。在求解微凸体侧接触问题时,还需要求解接触点处曲面的法向及切向向量。假设曲面z1的参数表达式如下所示
(5)
接触点处的方向向量可以由以下3个向量表示
(6)
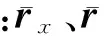
在己知接触点各方向向量后,总可以将该模型通过坐标变换的方式转化成标准的赫兹曲面弹性接触问题。但是,由于难以建立该坐标变换的数学模型,因此本文通过求解曲面曲率的方式将问题转化为标准的赫兹曲面接触问题。
1.3 接触点处的主曲率及其方向计算
本文采用Weingarten映射法求解曲面曲率。Weingarten映射是一种表征曲面某点处的单位法向量沿曲面某切线方向变化率的映射,该映射与空间坐标系及曲面参数方程的选取无关,可在接触点处建立曲面的自然活动标架场进行分析[15]。在Weingarten映射法中,令G、L分别为曲面第1基本形式和第2基本形式的系数[15]
(7)
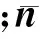
Weingarten映射本质上属于空间上的一种坐标变换。由微分几何[15]中的推导可得出G-1L是Weingarten映射的过渡矩阵,并且该过渡矩阵的特征值分别为κ1、κ2,特征向量分别为e1、e2,分别对应着曲面的主曲率及主曲率方向,即有如下对应关系[15]
(8)
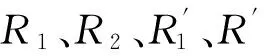
(9)

1.4 接触面积接触位移计算
Hertz讨论了曲面弹性点接触的受力分析[16]。如图1中坐标变换后的接触示意图所示,在曲面接触点处设新的坐标系,使得新坐标系的原点位于曲面接触的初始接触点处,xoy平面为接触点处的切平面,oz轴的方向为接触点的法向。经过合适地选取ox、oy方向,总可以使得新坐标系下结合面的法向接触间距满足以下公式[16]
(10)
法向接触间距的系数A、B与该点处两曲面在该接触点处的主曲率及其之间的夹角有关系,可以由以下两个公式计算得出[16]
(11)
(12)
曲面点接触的接触区域近似为椭圆,长、短半轴分别为[16]
(13)
式中:P代表接触点处的法向载荷;A、B是式(10)法向接触间距dn的两个系数;m、n是与椭圆积分相关的系数,数值可参考文献[16];k1、k2是与两微凸体的弹性模量有关的系数,具体表达式如下
(14)
式中:E为材料的弹性模量;ν为材料的泊松比。
接触位移与接触面积可由以下方程得出
(15)
式中:γ是与椭圆积分相关的系数,可参照文献[13]获得。
1.5 微凸体弹性接触力学模型的推广
由式(7)、式(8)可以看出,本模型的曲率计算仅与反映微凸体形状的曲面函数的一阶、二阶偏导数有关。若微凸体几何形状可以以二阶连续可导的二元函数表示,重复1.1节到1.4节的计算,均可得到微凸体接触点处的接触位移与接触面积。常用于描述微凸体几何外形的函数包括三角函数、二元高次函数、指数函数、幂函数等。例如,微凸体的二元高次函数拟合表达形式如下
(16)
式中:f(u,v)代表微凸体的几何函数;u、v是自变量,可以是笛卡尔坐标系下的变量,也可以是圆柱坐标系下的变量,可根据需要选择坐标系;a、b、c是与最终拟合形状有关的系数。此函数是具有连续的二阶偏导数,因此依然可以用前述的计算过程来计算两微凸体间接触变形与接触面积。
2 微凸体相对位置对接触的影响
通过上文的力学模型分析,获得了微凸体相对位置变化及椭圆率变化对接触位移δ与接触面积s的影响。微凸体形状采用式(2)描述,长度以μm为单位,取系数a为0.05,系数b为0.2,微凸体弹性模量为210 GPa,泊松比为0.3。以0.02 N的力向下压上微凸体z2,模型几何形状如图2所示。

图2 椭圆抛物体弹性接触模型
2.1 相对偏移及转角对接触的影响
采用两微凸体长半轴方向间的相对夹角α来表示两椭圆抛物体长轴间的夹角,用两微凸体中心线沿x轴方向上的相对位移dx来体现侧接触,y方向上的相对间距dy始终保持为0 μm,改变上微凸体与下微凸体的相对位置dx及夹角α,进行接触位移δ及接触面积s的计算,从而获得了不同相对位置dx及相对夹角α时,接触面积s与接触位移δ的变化规律。
如图3所示,微凸体长半轴方向间相对转角α对接触面积s的影响较小,微凸体中心线沿x方向相对间距dx对接触面积s的影响较大。在微凸体峰对峰接触时,α对接触面积s的影响较小,而随着dx增大,α对接触面积s的影响逐渐增大,面积波动从6.6%增大到12.5%。同时,在转角α一定、接触位移dx变动的情况下,接触面积s最大波动可达55.6%。

图3 相对偏移与转角对接触面积的影响
如图4所示,随着α及dx的增大,接触位移δ逐渐变小,波动幅度在20%左右,α及dx对接触位移δ的影响大致相同。
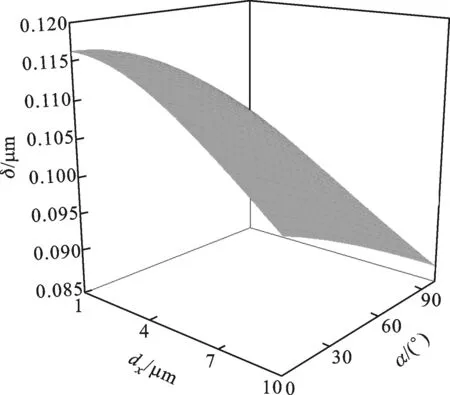
图4 相对偏移与转角对接触位移的影响
2.2 椭圆率与相对转角对接触的影响
微凸体的椭圆率ε可由式(1)中的参数a与b的关系来表征。椭圆抛物体的各个水平截面的ε相同,本文采用ε来表征微凸体的椭圆程度,并计算了在dx为8 μm、dy为0 μm的情况下,ε变化与α变化对接触面积s与接触位移δ的影响。椭圆率ε表达式为
(17)
如图5所示,椭圆率ε对接触面积s的影响较大,ε增加会导致s迅速减小,在ε超过0.9之后,s急剧下降,最大波动达27%,造成的应力集中现象较为明显。同时,相对于椭圆率ε,α对接触面积s的影响较小。在相同ε的情况下,α对接触面积s的波动在0.014%与10%之间。

图5 椭圆率与微凸体相对转角对接触面积的影响
如图6所示,椭圆率ε增加会导致接触位移δ迅速增加,在ε超过0.9之后,δ急剧上升。在椭圆率一定的情况下,接触位移δ基本恒定,α对δ的影响较小,只有在椭圆率ε偏大的情况下α的变动会导致δ变动加大。
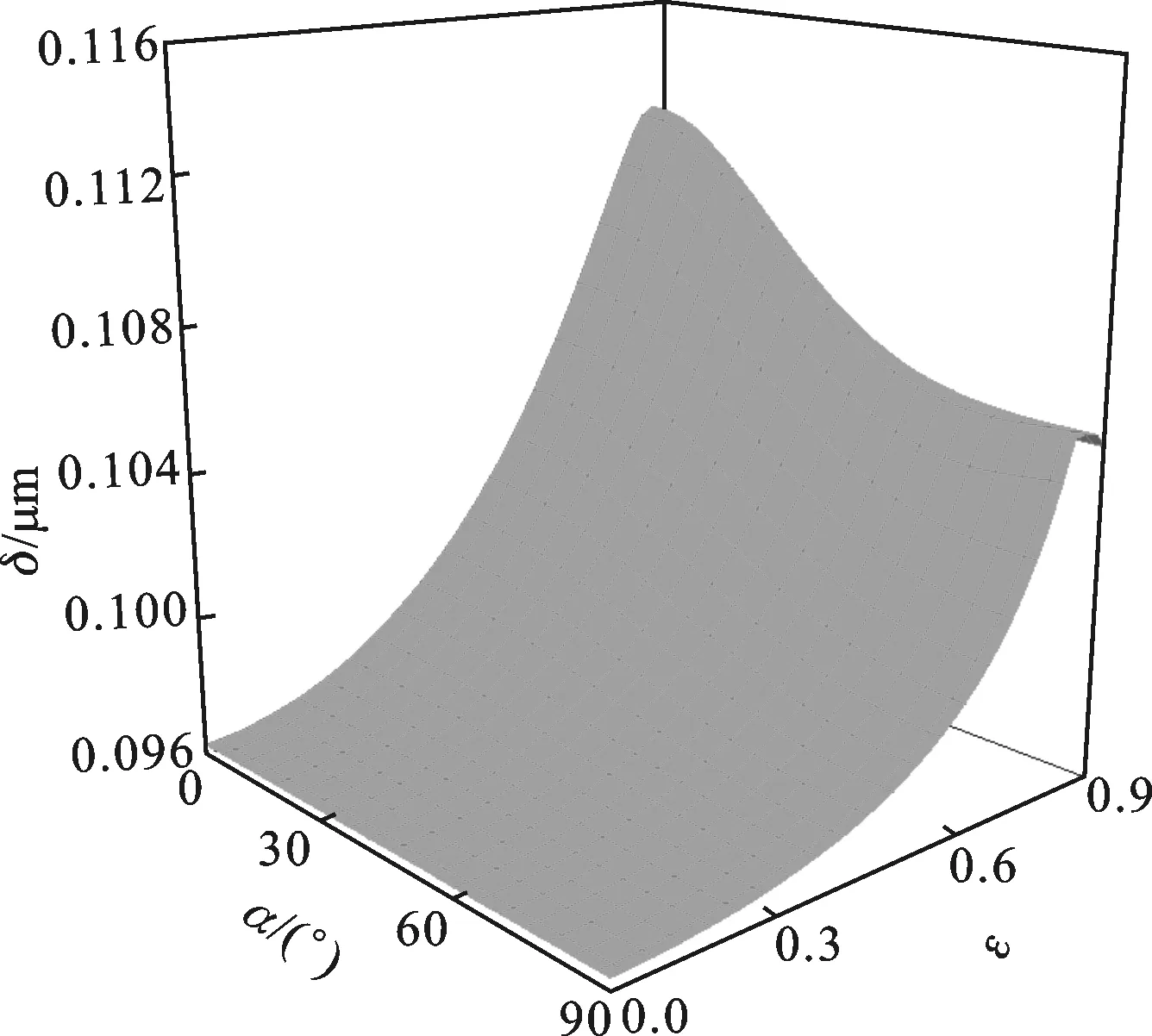
图6 椭圆率与微凸体相对转角对接触位移的影响
3 本文模型与仿真模型对比
3.1 本文模型算例
为与有限元模型对比,建立了特定椭圆抛物体接触的计算模型。模型中上、下抛物面的参数a、b相同,符合下式所描述的形状(单位为μm)
z=0.05x2+0.2y2
(18)
材料的弹性模量为210 GPa,泊松比为0.3。接触间距dn为0作为初始状态,将上微凸体下压0.2 μm。为了增加对比点的随机性,以便于对理论解析模型与有限元模型进行全面对比,如图 7所示,令上微凸体与下微凸体长半轴间的夹角α成45°,其中心线沿以下微凸体中心为圆心、半径为8 μm的圆弧轨迹移动,β按逆时针方向从0°到180°分布11个对比点,增加了接触位置的随机性。
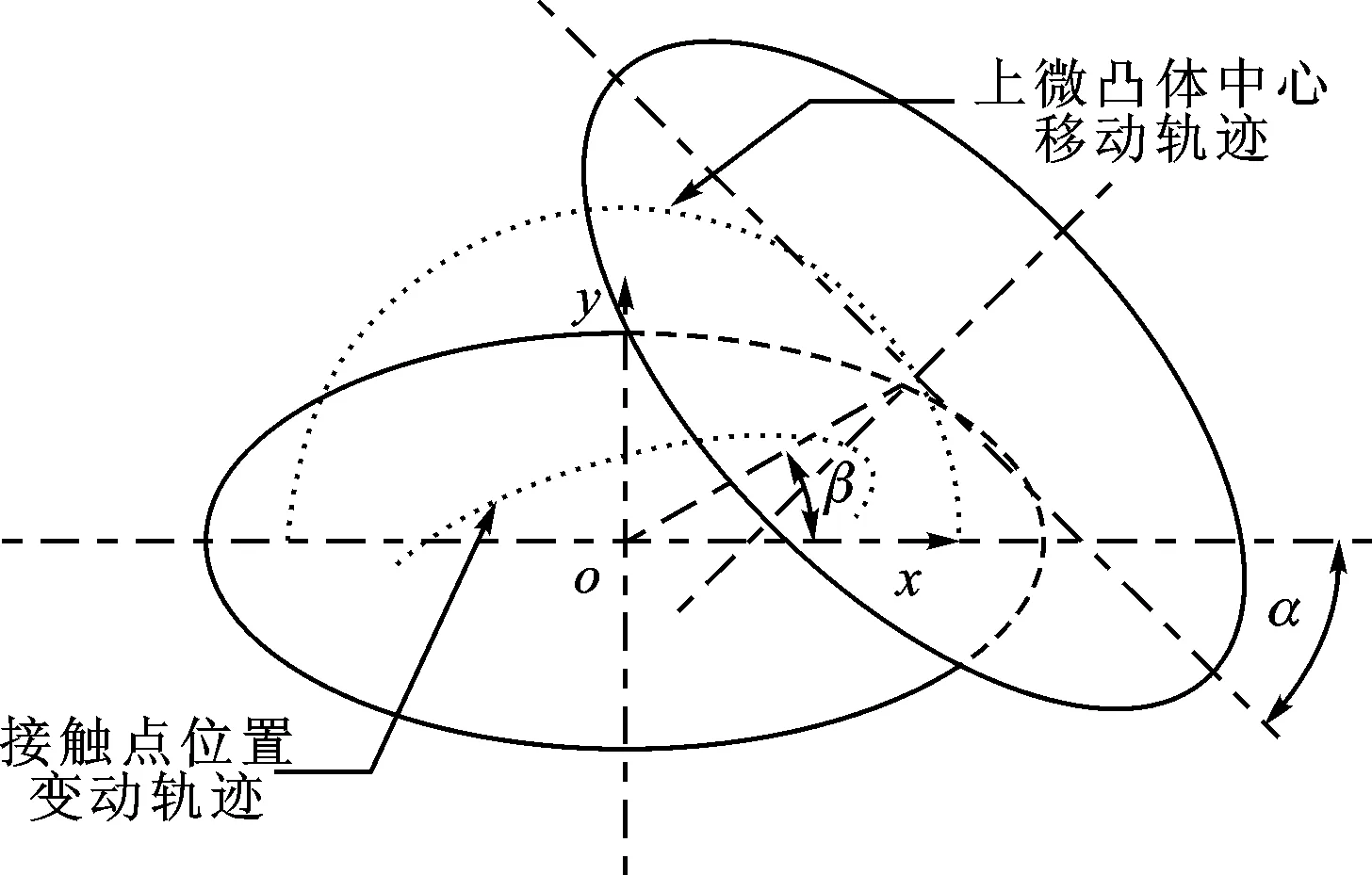
图7 椭圆抛物体弹性接触对比模型
3.2 椭圆抛物体接触有限元模型
按3.1节所述的几何形状,相对位置关系及材料特性建立了有限元分析模型。ABAQUS有限元模型采用C3D4线性四面体单元,网格边长约为0.6 μm。由于分析接触面积s及接触位移δ时,接触点处网格数目要求较高,需进行细分,细分后接触点附近网格边长约为0.04 μm,最终总的单元数目约为11万。下微凸体底面施加端固定约束,上微凸体顶面约束水平方向自由度,并施加垂直方向的位移,大小为0.2 μm。取初始接触点(xc,yc)相对基体的下陷量之和作为接触位移δ。按照1.1节中的假设(3),在有限元模型当中,忽略摩擦力的影响,接触的摩擦系数设置为0。最终的有限元模型如图8所示。
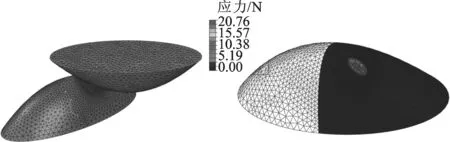
(a)有限元分析网格 (b)有限元分析结果图8 有限元分析模型网格及最终计算结果
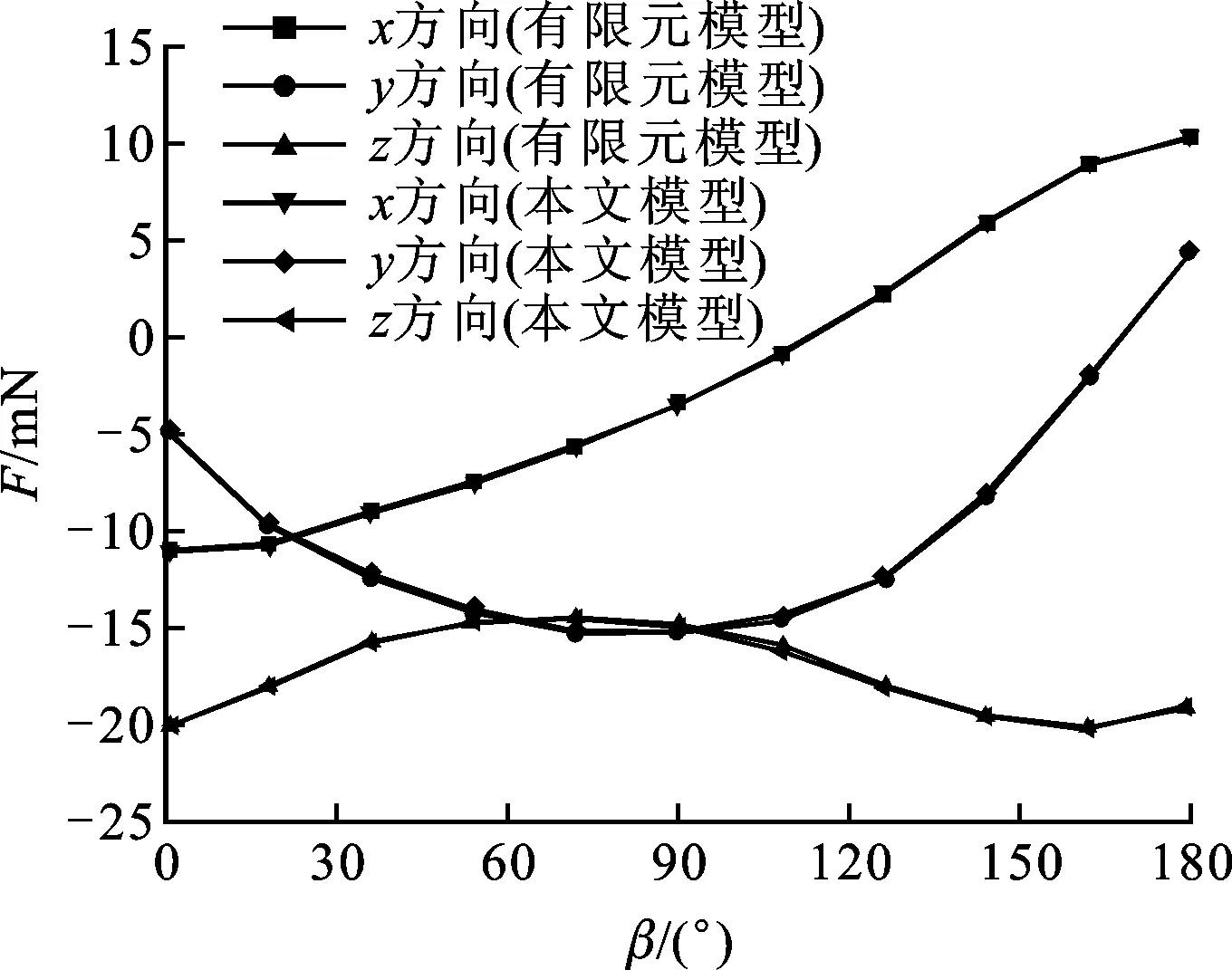
图9 两种方法沿坐标轴方向分力对比
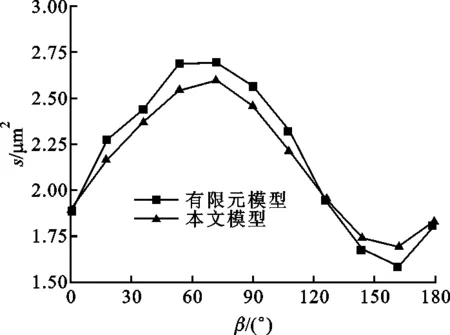
图10 两种方法接触面积对比
3.3 模型计算结果对比
本文模型与有限元模型各方向分力F对比如图9所示。不同点接触时3个方向分力符合较好,最大相对误差不超过1%,可见本文模型与有限元模型在力学分析结果上较为符合。
由图10可得,与有限元模型相比,本文接触面积理论计算结果最大误差为6.2%,表明本文的理论模型可以在一定误差范围内与有限元法计算结果近似。
由图11可得,对于接触间距,本文理论计算结果与有限元结果偏差最大为10%。
由于结合面处的接触面积非常小,计算结果对网格密度非常敏感,而为了保证计算效率,难以将网格划分得十分精细,因此有限元结果中的接触面积和接触位移与本文的理论模型结果相比,误差相对较大。由于各方向上的分力是施加在整个模型上的,是一种总力,受网格密度影响较小,因此各方向分力的误差较小。

图11 两种方法接触位移对比
4 结 论
(1)本文提出了一种新型微凸体弹性接触模型,用椭圆抛物体作为微凸体的几何模型,能更好地体现微凸体接触中的侧接触特性。本文的弹性接触计算同样适用于求解几何模型具有连续二阶偏导数的微凸体模型的弹性接触问题,为以后进一步研究形状更为复杂的微凸体接触奠定了基础。
(2)通过Weingarten映射的方法求解了微凸体接触点处的曲面曲率,并利用赫兹曲面接触理论求解,最终得出接触面积s与接触位移δ的解析结果,并与有限元分析结果进行了对比。对比结果表明,接触位移计算结果差异最大为10%,接触面积结果最大差异为6.2%。
(3)分析了微凸体相对接触位置及椭圆率与接触面积、接触位移的关系。其中,椭圆率在超过0.9后,接触面积迅速减小,接触位移迅速增大;相对平移位置和转角相比,对接触位移与接触面积的影响较大。
[1] GREENWOOD J, WILLIAMSON J. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1966, 295(1442): 300-319.
[2] CHANG W, ETSION I, BOGY D B. An elastic-plastic model for the contact of rough surfaces [J]. Journal of Tribology, 1987, 109(2): 257-263.
[3] ZHAO Y, MAIETTA D M, CHANG L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow [J]. Journal of Tribology, 2000, 122(1): 86-93.
[4] WHITEHOUSE D J, ARCHARD J. The properties of random surfaces of significance in their contact [J]. Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1970, 316(1524): 97-121.
[5] LIOU J L, LIN J F. A microcontact non-Gaussian surface roughness model accounting for elastic recovery [J]. Journal of Applied Mechanics, 2008, 75(3): 031015.
[6] KIM T, BHUSHAN B, CHO Y. The contact behavior of elastic/plastic non-Gaussian rough surfaces [J]. Tribology Letters, 2006, 22(1): 1-13.
[7] JAMARI J, SCHIPPER D. An elastic-plastic contact model of ellipsoid bodies [J]. Tribology Letters, 2006, 21(3): 262-271.
[8] BUCZKOWSKI R, KLEIBER M. Statistical models of rough surfaces for finite element 3D-contact analysis [J]. Archives of Computational Methods in Engineering, 2009, 16(4): 399-424.
[9] CIULLI E, FERREIRA L, PUGLIESE G, et al. Rough contacts between actual engineering surfaces: part I Simple models for roughness description [J]. Wear, 2008, 264(11): 1105-1115.
[10]SEPEHRI A, FARHANG K. Closed-form equations for three dimensional elastic-plastic contact of nominally flat rough surfaces [J]. Journal of Tribology, 2009, 131(4): 041402.
[11]庄艳, 李宝童, 洪军, 等. 一种结合面法向接触刚度计算模型的构建 [J]. 上海交通大学学报, 2013, 47(2): 180-186. ZHUANG Yan, LI Baotong, HONG Jun, et al. A normal contact stiffness model of the interface [J]. Journal of Shanghai Jiaotong University, 2013, 47(2): 180-186.
[12]GREENWOOD J, WU J. Surface roughness and contact: an apology [J]. Meccanica, 2001, 36(6): 617-630.
[13]ANTOINE J, ABBA G, VISA C, et al. Approximate analytical model for Hertzian elliptical contact problems [J]. Journal of Tribology, 2006, 128(3): 660-664.
[14]SEPEHRI A, FARHANG K. On elastic interaction of nominally flat rough surfaces [J]. Journal of Tribology, 2008, 130(1): 011014.
[15]徐森林, 纪永强, 金亚东, 等. 微分几何 [M]. 合肥: 中国科学技术大学出版社, 2013: 169-180.
[16]TIMOSHENKO S P, GOODIER J N. 弹性理论 [M]. 3版. 徐芝纶, 译. 北京: 高等教育出版社, 2013: 377 -381.
(编辑 杜秀杰)
Elastic Contact Model of Elliptical Parabolic Asperity
LIU Weiqiang,ZHANG Jinhua,HONG Jun,ZHU Linbo
(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
To precisely describe the contact mechanics between two solid rough surfaces, a kind of elliptical parabolic elastic asperity contact model was proposed. Both top-top contact and shoulder-shoulder contact were considered in this model. Weingarten map was adopted to obtain the curvature of contact point, and Hertz surface contact theory was used to solve this model. Analytic formula was deduced to get contact displacement and contact area for shoulder-shoulder contact. The influence of relative location and ellipticity on contact area and contact displacement was discussed. Finite element model and the proposed model were compared. The result shows that the ellipticity exerts an obvious influence on the contact area and contact displacement; when ellipticity exceeds 0.9, the contact area and contact displacement of two asperities change drastically; the largest contact displacement error reaches 10%, and the largest contact area error reaches 6.2%. The proposed model is suitable for the other asperity models with second-order continuous partial derivatives.
Hertz surface contact; asperity; elastic contact
2015-04-15。
刘伟强(1988—),男,硕士生;洪军(通信作者),男,教授,博士生导师。
国家重点基础研究发展计划资助项目(2011CB706600);国家高技术研究发展计划资助项目(2012AA040701)。
时间:2015-06-29
10.7652/xjtuxb201510006
O343.3
A
0253-987X(2015)10-0034-07
网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150629.1137.001.html
