非一致噪声下的多阵列直接定位算法

黄志英,吴江,唐涛,王云龙

(解放军信息工程大学信息系统工程学院, 450001, 郑州)



非一致噪声下的多阵列直接定位算法

黄志英,吴江,唐涛,王云龙

(解放军信息工程大学信息系统工程学院, 450001, 郑州)

针对实际无源定位系统中多个阵列分散分布以及单个阵列各阵元之间差异造成的噪声功率分布不均匀导致直接定位(DPD)算法精度下降的问题,提出了一种非一致高斯白噪声场中的多阵列最大似然DPD(UN-ML-DPD)算法,并推导出该条件下的克拉美罗界。首先计算各阵列输出协方差矩阵;再将计算结果传到数据处理中心;然后由数据中心通过迭代的方式同时对目标位置与非一致噪声功率进行最大似然联合估计,以收敛后得到的结果作为目标位置精确估计值,从而减弱了非一致噪声对DPD算法的影响;最后在多目标条件下用交替投影法降低算法复杂度。较之传统算法,UN-ML-DPD算法能够提高多阵列在低信噪比下的定位精度。仿真结果表明:UN-ML-DPD算法在-15 dB的低信噪比下估计误差小于15 km,与DPD算法相比定位精度提高15%以上;能较为准确地估计各阵列噪声协方差矩阵,在标准噪声功率小于30 W时估计误差小于3.5 W;在高信噪比下定位精度能够逼近克拉美罗下界。

无源定位;多阵列;非一致噪声;直接定位;最大似然估计

传统的多阵列角度交叉定位方法需要2步:各站首先利用各自的固定阵列对窄带信号到达方向(direction of arrival, DOA)进行估计,并将DOA估计值通过网络传输到融合中心;融合中心根据各站的DOA估计值进行联合交叉定位[1-2]。这种方式对DOA的估计由各站孤立完成,忽略了各站收到的信号都是来自同一个辐射源的约束,而且参数估计与位置解算相分离造成了测量的参数与真实目标位置失配,导致数据处理过程中信息不可避免的损失,从而无法获得最优的估计性能[3]。

针对传统2步定位模型的缺点,近年来学者们提出了对辐射信号的一步直接定位(direct position determination, DPD)算法,其思想是不预先估计信号到达方向(DOA)或者到达时间差(TDOA),直接用原始数据通过最大似然等方式对目标的位置进行非线性估计。这些算法在低信噪比下较传统的2步定位方法具有较高的精度,且能够在低信噪比下逼近相应的克拉美罗下界(Cramér-Rao lower bound, CRLB)。根据处理的目标数据,该类算法可以分为频域数据DPD[4-7]与时域数据DPD[8-9]2种。频域数据DPD精度最高,但不适用于超视距定位模型;时域数据DPD精度比频域数据DPD精度稍低,但仍高于传统2步定位法,且适用于超视距定位。

传统的DPD算法都基于一个基本假设,即各阵列的接收噪声都符合均值为零方差为δ2的高斯分布,然而实际中并非如此。对于多个分布在不同位置的阵列,由于各阵列间相隔较远,不同的电磁环境下阵列的接收噪声是有差异的;此外,在同一个阵列中,由于接收通道间的互耦、分布源引起的随机散射、回声以及非期望干扰等原因,也有可能造成各阵元之间噪声的非均匀分布[12]。对噪声建模的误差将会导致DPD算法性能的下降。

针对上述问题,本文对多阵列接收噪声进行建模,为了与传统的单阵列非均匀噪声相区分[12],定义多阵列非一致接收噪声为:

(1)各阵列的接收噪声为相互独立的高斯白噪声,功率未知且不相等;

(2)同一阵列不同阵元之间的接收噪声相互独立,功率未知且不相等。

基于文献[12]在非均匀噪声下的DOA与阵列噪声协方差矩阵联合估计的算法,本文提出了一种基于多阵列的非一致噪声下的最大似然直接定位算法(unknown nonuniform noise maximum likelihood direct position determination, UN-ML-DPD),该算法通过交替迭代的方式对各阵列的噪声协方差矩阵以及目标位置进行联合估计。本文算法属于时域数据处理方式,与文献[8-9]算法相比,在非一致噪声下能够取得更好的定位效果。在信噪比较高的条件下,本文算法的定位性能接近相应的克拉美罗下界。

1 观测模型

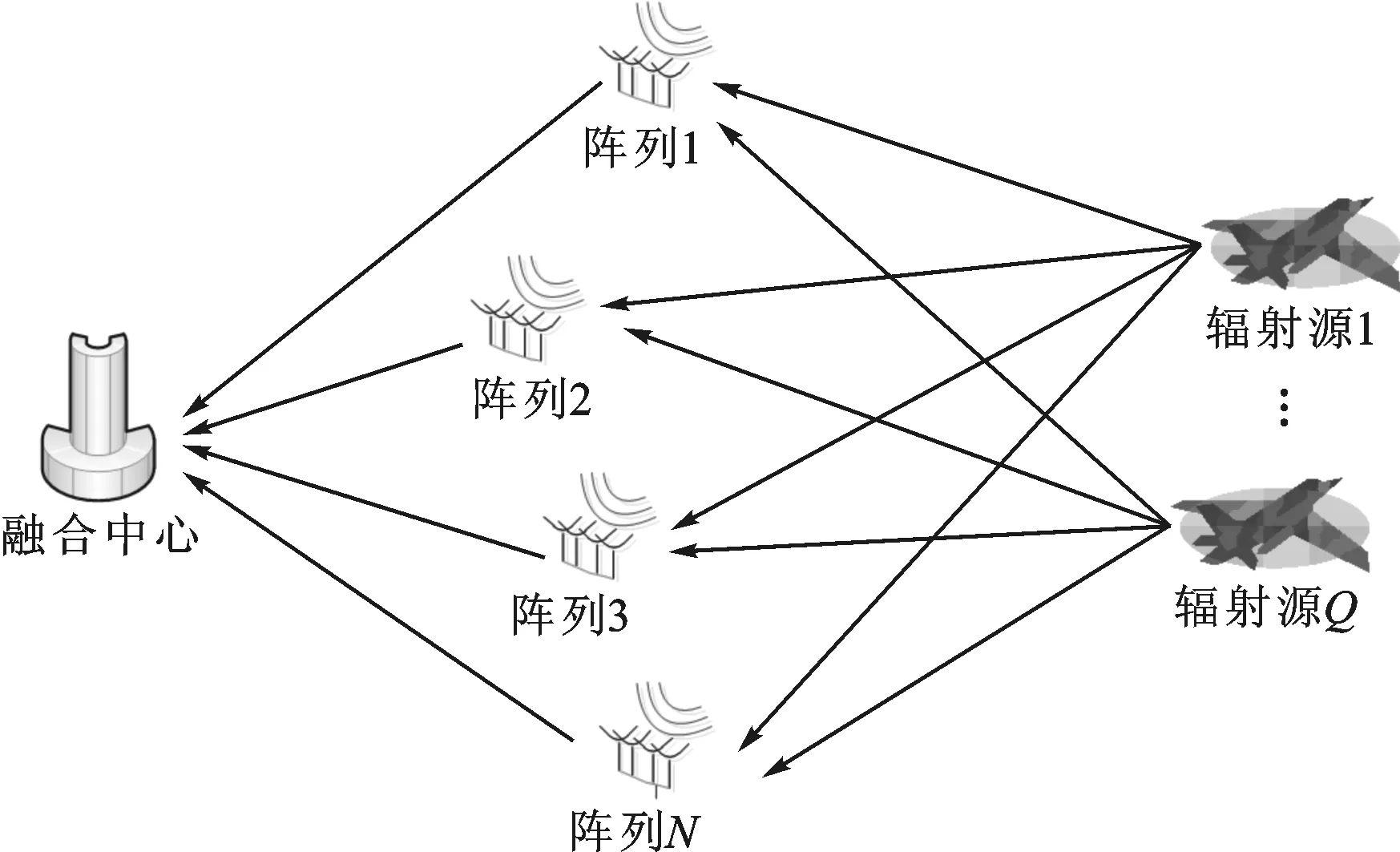
图1 多站联合定位示意图

多阵列典型的定位场景如图1。假设多阵列联合定位系统中,sn,k,q表示k时刻入射到第n个阵列的第q个源信号,其中n=1,…,N,N为联合定位系统中阵列的个数,q=1,…,Q,Q为辐射源个数,k=1,…,K,K为采样个数。令zn,k∈CMn×1表示第n个站k时刻的接收矩阵,Mn为第n个阵列的阵元个数,则有

(1)

式中:wn,k∈CMn×1为第n个站的噪声矩阵;an(pq)∈CMn×1为阵列流型矢量;pq=[xq,yq]T为第q个辐射源的二维平面位置。令

(2)

则有

(3)

再令

(4)

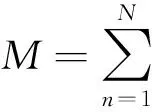
(5)

由此,接收信号与辐射源的位置关系可由式(5)确定,则多阵列联合定位的问题可以归结为:利用接收矩阵vk估计所有辐射源的位置p。为了解决上述联合定位问题,需要以下2个基本假设。

假设1 多阵列接收噪声与接收信号相互独立,且为非一致噪声,接收噪声矩阵wk的协方差矩阵为

(6)

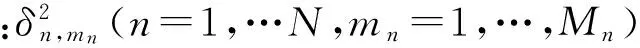
(7)

假设2sn,k是一组待估计的确定信号序列(确定信号数据模型),接收信号zk符合正态分布

(8)

(9)

2 算法原理

2.1 定位算法原理

在信号波形为未知确定信号序列的假设下,对于第n个阵列,n=1,…,N,令

(10)

则(3)式可以写成

Zn=An(p)Sn+Wn

(11)

再令

(12)

式中cn,k∈CMn×1(k=1,…,K)和rn,m∈C1×K(m=1,…,Mn)分别表示矩阵Gn的第k列和第m行,则在固定其他参数的情况下,第n个阵列的噪声协方差矩阵的最大似然估计为[12]

(13)

在固定其他参数的情况下,sn,k的最大似然估计为

(14)

式中

(15)

时域数据DPD算法的最大似然估计器可将下式最小化[9]

(16)

将式(14)代入式(16),得到目标位置p的最大似然估计为

(17)

式中

(18)

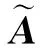
(19)

在联合定位系统中,定义非一致噪声下的多阵列最大似然DPD的代价函数为

(20)

式(20)并不能同时对噪声的协方差矩阵和目标位置进行估计。因为根据该式的形式可知,目标位置p的估计依赖于根据式(13)对各阵列协方差矩阵Φn的估计;反之,Φn的估计也通过式(14)依赖于目标位置p。通过迭代的方式,可以实现Φn和p的联合估计。

2.2 交替投影算法

本文提出的UN-ML-DPD算法是一个非线性的多维最优化问题,需要全局极值的多维搜索。在单目标的情况下,该算法只需要在二维平面上对目标位置进行搜索,而在多目标条件下,则需要2Q维的搜索,在目标数增多的时候算法的计算量会随着搜索维数的增多而急剧增大。为了降低算法的搜索维数,本文采用文献[9]提出的交替投影DPD(alternative projection DPD,AP-DPD)算法来解决本文算法的多维优化问题,其基本思想是通过迭代的方式将多维优化问题进行简单求解,在每一次迭代的每一步中,均相对于一个目标进行优化,而其他参数保持不变。于是迭代过程中的每一步均只需要进行一次二维的搜索。

(21)

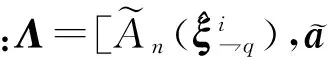
(22)

对于任意具有相同行数的矩阵E和F,P[E,F]为矩阵[E,F]的列张成的子空间投影矩阵,则根据分块Hermite矩阵的求逆公式可得

(23)

式中:FE=(I-PF)E。于是

(24)

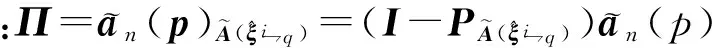
(25)

则式(21)可以表示为

(26)

综上所述,UN-ML-DPD算法的主要步骤如下。

(4)重复步骤2和步骤3直至得到最后目标位置p的估计值。

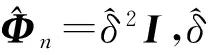
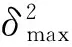
(27)

同时,为了考察算法在不同噪声环境下的定位性能,定义非一致噪声条件下的信噪比

(28)

式中:Pn=E[|sn,k|2]为第n个阵列接收信号功率。

假设传统时域数据DPD算法对目标定位搜索的平均计算量为Cp。本文算法需要联合估计目标位置p和噪声协方差矩阵Φ,并需要一定次数的迭代,假设估计Φ的计算量为CΦ,算法收敛所需要的平均迭代次数为L,则本文算法定位平均计算量为L(Cp+CΦ)。由于Φn估计的计算量主要集中在式(14)的矩阵计算中,式(17)的计算与式(14)相当,若采用QPSO算法实现p的最优化,假设使用u个粒子进行搜索,QPSO算法收敛需要的平均迭代次数为v,则式(17)计算就需要进行uv次,因此在通常情况下Cp≫CΦ,即本文算法定位平均计算量约为传统算法的L倍。

3 定位误差的克拉美罗下界

本章将分析非一致噪声下多阵列DPD算法的克拉美罗下界(CRLB)。待估计的所有未知参数组成的矢量为

(29)

CRLB由Fisher信息矩阵的逆给出,有

(30)

式中

(31)

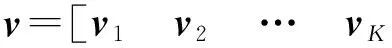
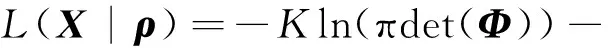
(32)

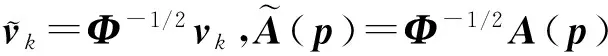
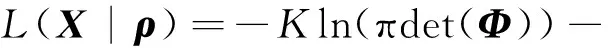
(33)

使用类似于文献[12]的计算方法,可得

(34)

式中

(35)

(36)

(37)

其中⊗表示Kronecker积。

4 仿真实验

为了验证本文算法的性能,对于不同的场景均做1 000次Monte-Carlo实验,并与文献[8]中SDF-DPD以及文献[9]中ML-DPD这2种时域数据DPD算法性能进行比较。本文的所有仿真均将采用以下典型定位场景:假设目标位置为(300 km,200 km)。多阵列联合定位系统有4个测量站,其坐标分别为(0 km,80 km)、(150 km,0 km)、(0 km,200 km)、(100 km,300 km),目标与测量站的位置关系如图2所示。

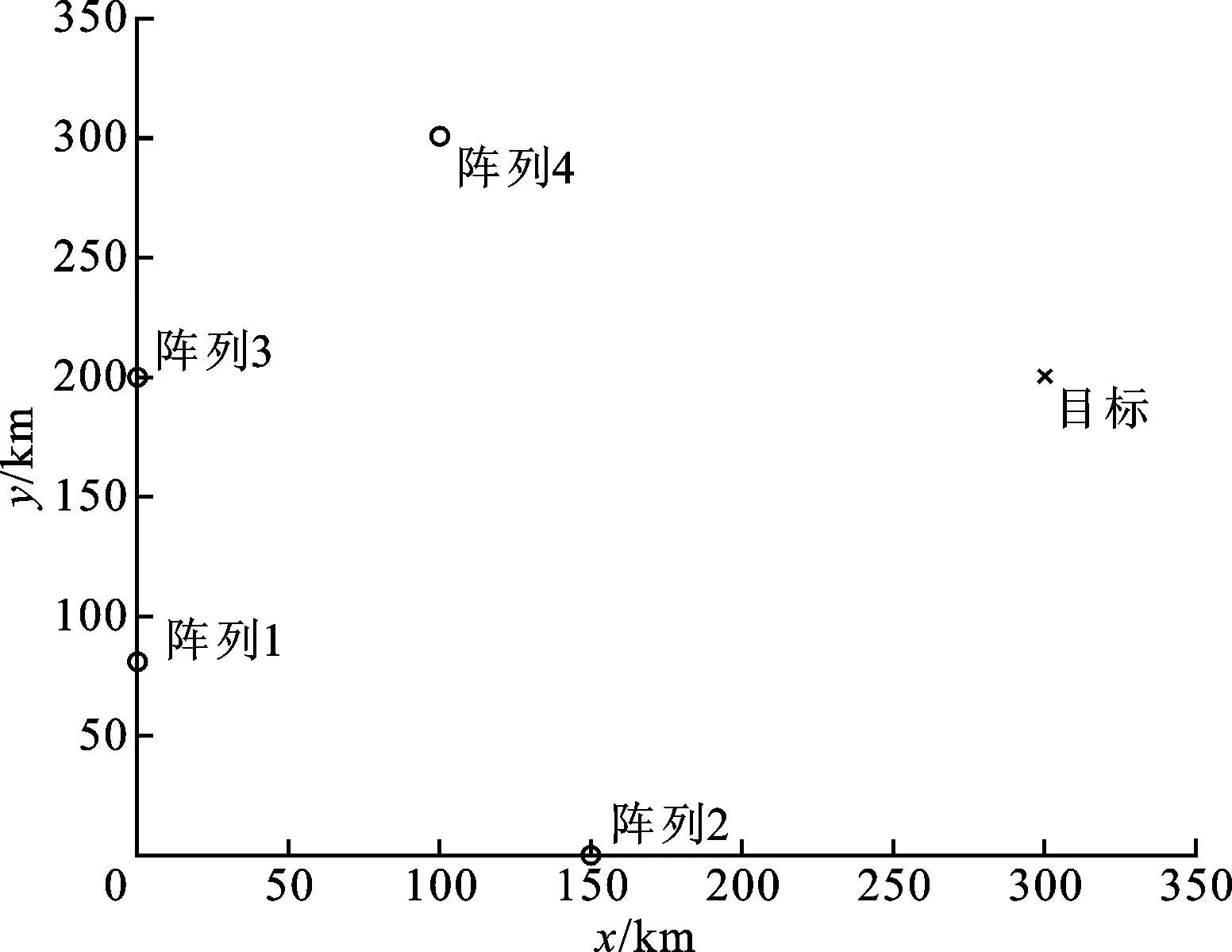
图2 目标与测量站位置关系图

联合定位系统中所有阵列都是阵元个数为10的平行于y轴的均匀直线阵,阵元间距与信号波长的比值d/λ=0.5。信噪比为-5 dB,快拍数为32,信噪比范围为-15～0 dB,用定位均方误差eRMSE考察算法在不同信噪比下的定位性能,固定各阵列接收噪声协方差矩阵为

(38)

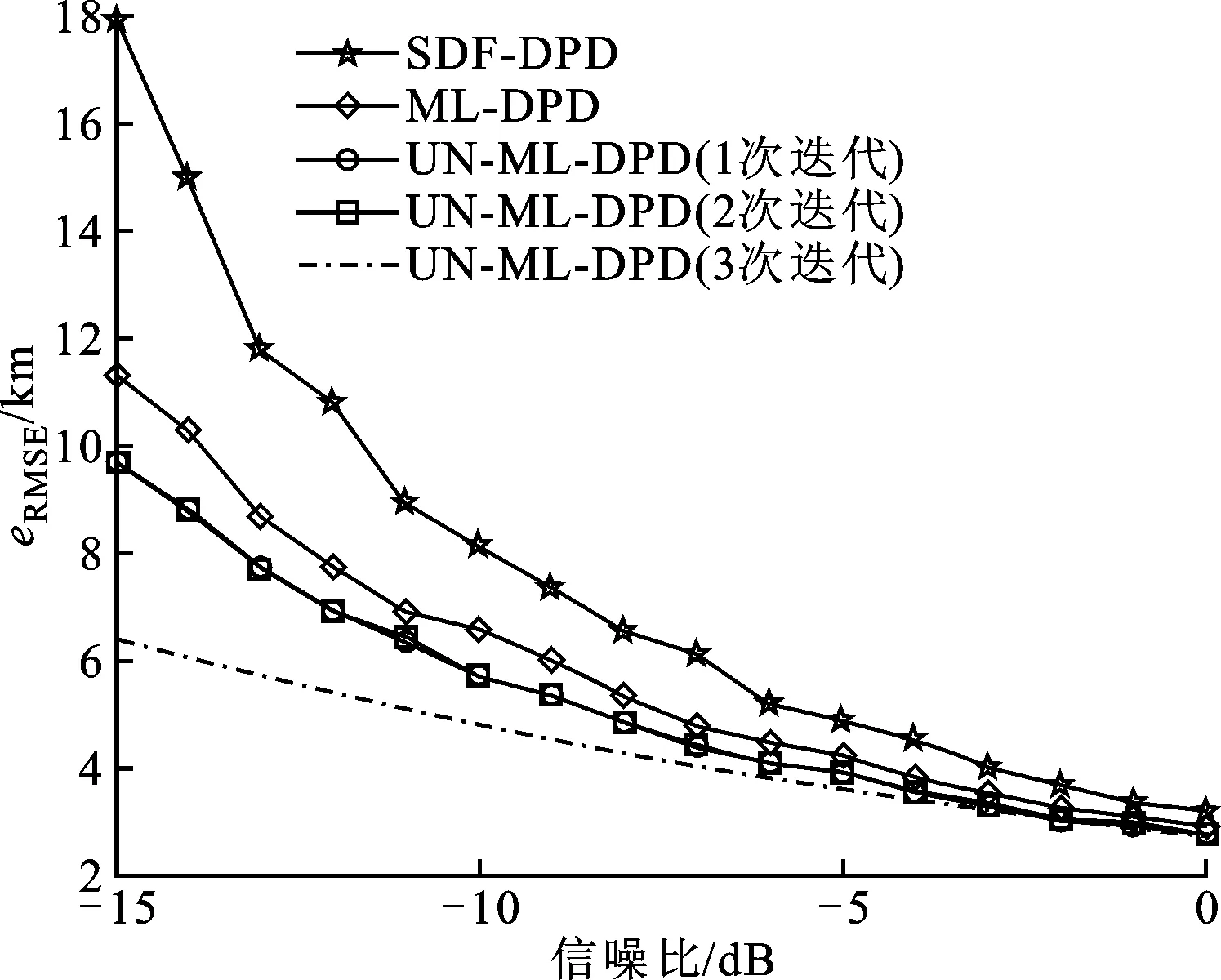
图3 不同信噪比下3种算法的性能对比

考察算法在不同最劣噪声功率比下的定位性能,其他仿真条件不变,信噪比固定为-5dB,阵列的噪声协方差矩阵设置如下

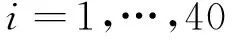
(39)

采用二次迭代后得到的位置估计值作为算法定位的最终估计值,得到的结果如图4所示。可以看到,最劣噪声功率比越大,本文算法的精度较其他2种算法的提升效果越明显。

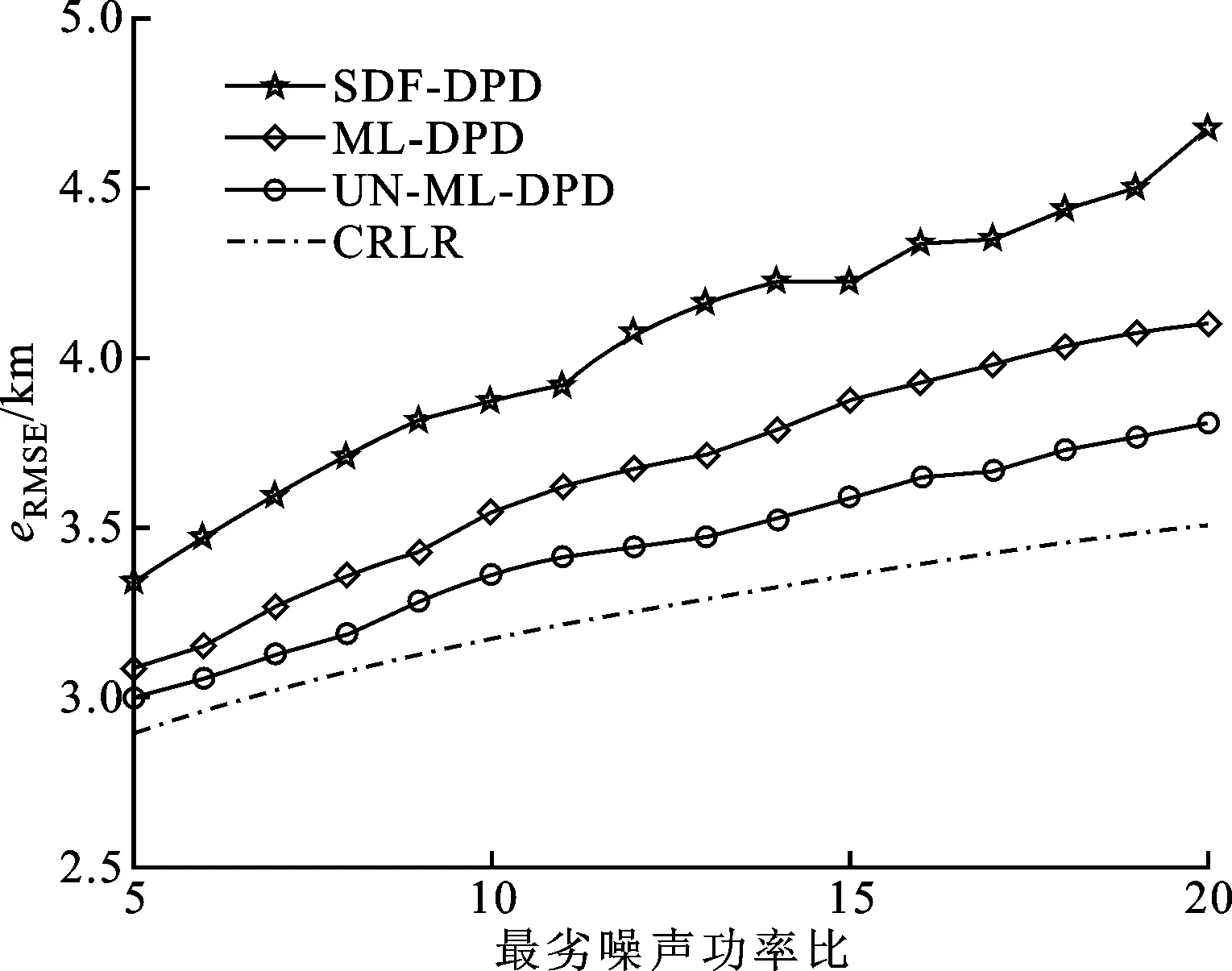
图4 不同最劣噪声功率比下3种算法的定位性能对比

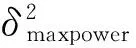
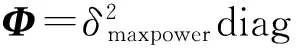
(40)

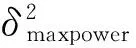
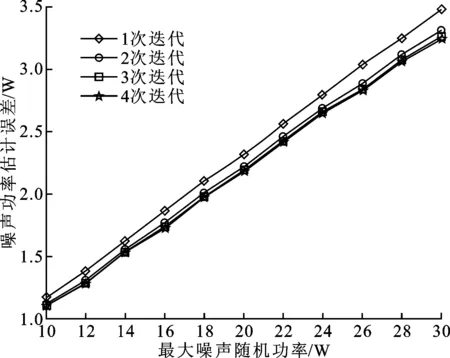
图5 不同迭代次数下阵元噪声功率估计误差随最大噪声随机功率的变化曲线

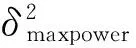
假设监测区域内存在2个目标,其位置分别为(300 km,200 km)和(300 km,100 km),内外层各迭代3次,其他条件与图3相同,得到的2个目标条件下的定位均方误差与信噪比之间的关系如图6和图7所示。可以看到,在2个目标且噪声非均匀的条件下,SDF-DPD算法受非一致噪声的影响最大,性能最为不稳定,而采用交替投影方式的本文算法与ML-DPD依然可以同时对2个目标较为稳定的进行位置估计,定位精度均高于SDF-DPD算法。经过3次迭代本文算法的精度趋于稳定,精度比均匀噪声假设的ML-DPD算法高。且在信噪比较高时对2个目标的定位性能均能逼近克拉美罗下界。

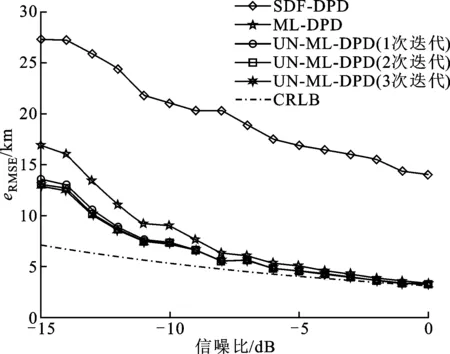
图6 不同信噪比下3种算法的定位性能对比(目标1)

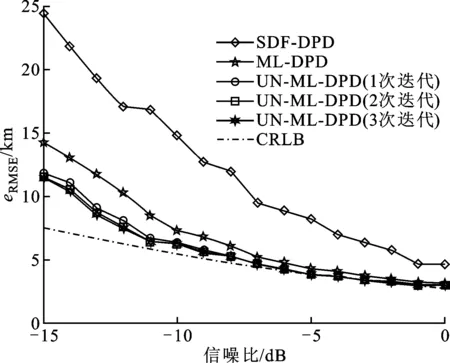
图7 不同信噪比下3种算法的定位性能对比(目标2)

5 结 论

考虑各阵列之间与单个阵元之间的差异造成的接收噪声非均匀的情况,本文的多阵列直接定位算法通过迭代的方法对阵列接收噪声协方差矩阵与目标位置进行联合估计,降低了非一致噪声对时域数据DPD算法的影响,提高了该算法的精度,且在信噪比较低及最劣噪声功率比较大的情况下提升效果较为明显。本文算法在信噪比较高的条件下可以逼近克拉美罗下界。在单目标条件下,由于需要的迭代次数不多,本文算法较之传统DPD算法的计算量并未显著增加,但在多目标条件下,由于本文算法的定位解算过程需要2层迭代,实现较为复杂,因此计算量较大。

[1] 王鼎, 吴瑛, 田建春. 基于总体最小二乘算法的多站无源定位 [J]. 信号处理, 2007, 23(4): 611-614. WANG Ding, WU Ying, TIAN Jianchun. Multi-station passive location based on TLS algorithm [J]. Signal Processing, 2007, 23(4): 611-614.

[2] 王鼎, 张莉, 吴瑛. 基于角度信息的结构总体最小二乘无源定位算法 [J]. 中国科学: F辑 信息科学, 2009, 39(6): 663-672. WANG Ding, ZHANG Li, WU Ying. The structured total least squares algorithm research for passive location based on angle information [J]. Science in China: Series F Information Science, 2009, 39(6): 663-672.

[3] 王云龙, 吴瑛. 联合时延与多普勒频率的直接定位改进算法 [J]. 西安交通大学学报, 2015, 49(4): 123-129. WANG Yunlong, WU Ying. An improved direct position determination algorithm with combined time delay and Doppler [J]. Jounal of Xi’an Jiaotong University, 2015, 49(4): 123-129.

[4] WEISS A J. Direct position determination of narrowband radio frequency transmitters [J]. IEEE Signal Processing Letters, 2004, 11(5): 513-516.

[5] AMAR A, WEISS A J. Advances in direct position determination [C]∥ Proceedings of 2004 Sensor Array and Multichannel Signal Processing Workshop. Los Alamitos, CA, USA: IEEE Computer Society, 2004: 584-588.

[6] WEISS A J, AMAR A. Direct position determination of multiple radio signals [J]. EURASIP Journal on Applied Signal Processing, 2005(1): 37-49.

[7] AMAR A, WEISS A J. Direct position determination in the presence of model errors: known waveforms [J]. Digital Signal Processing, 2006, 16: 52-83.

[8] DEMISSIE B, OISPUU M, RUTHOTTO E. Localization of multiple sources with a moving array using subspace data fusion [C]∥ 11th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2008: 1-7.

[9] OISPUU M, NICKEL U. Direct detection and position determination of multiple sources with intermittent emission [J]. Signal Processing, 2010, 90: 3056-3064.

[10]张敏, 郭福成, 周一宇. 基于单个长基线干涉仪的运动单站直接定位 [J]. 航空学报, 2013, 34(2): 378-386. ZHANG Min, GUO Fucheng, ZHOU Yiyu. A single moving observer direct position determination method using a long baseline interferometer [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 378-386.

[11]孙俊, 方伟, 吴小俊, 等. 量子行为粒子群优化: 原理及其应用 [M]. 北京: 清华大学出版社, 2011.

[12]PESAVENTO M, GERSHMAN A B. Maximum-likelihood direction-of-arrival estimation in the presence of unknown nonuniform noise [J]. IEEE Transactions on Signal Processing, 2001, 49(7): 1310-1324.

[13]王永良, 陈辉, 彭应宁. 空间谱估计理论与算法 [M]. 北京: 清华大学出版社, 2004.

[本刊相关文献链接]

王云龙,吴瑛.联合时延与多普勒频率的直接定位改进算法.2015,49(4):123-129.[doi:10.7652/xjtuxb201504020]

张东伟,郭英,齐子森,等.采用空间极化时频分布的跳频信号多参数联合估计算法.2015,49(8):17-23.[doi:10.7652/xjtuxb201508004]

巴斌,郑娜娥,朱世磊,等.利用蒙特卡罗的最大似然时延估计算法.2015,49(8):24-30.[doi:10.7652/xjtuxb201508005]

吴一全,孟天亮,吴诗婳.人工蜂群优化的非下采样Shearlet域引导滤波图像增强.2015,49(6):39-45.[doi:10.7652/xjtuxb201506007]

熊涛,江桦,崔鹏辉,等.应用基扩展模型的混合信号单通道盲分离算法.2015,49(6):60-66.[doi:10.7652/xjtuxb201506 010]

尚佳栋,王祖林,周丽娜,等.采用随机共振增强的混合扩频信号跳频参数估计.2014,48(10):42-48.[doi:10.7652/xjtuxb201410007]

吴杰,冯祖仁,刘恒,等.水下目标多元声传感阵列网络定位方法.2015,49(4):40-45.[doi:10.7652/xjtuxb201504007]

李彬,王文杰,殷勤业,等.无线传感器网络节点协作的节能路由传输.2012,46(6):1-6.[doi:10.7652/xjtuxb201206001]

朱磊,水鹏朗,章为川,等.利用区域划分的合成孔径雷达图像相干斑抑制算法.2012,46(10):83-88.[doi:10.7652/xjtuxb201210015]

(编辑 刘杨)

A Direct Position Determination Algorithm Based on Multi Arrays in the Presence of Unknown Nonuniform Noise

HUANG Zhiying,WU Jiang,TANG Tao,WANG Yunlong

(Institute of Information System Engineering, Information Engineering University of PLA, Zhengzhou 450001, China)

A multi-array based maximum likelihood direct position determination (DPD) algorithm in the presence of unknown nonuniform noise (UN-ML-DPD) is proposed and an expression of Cramér-Rao lower bound (CRLB) is derived to solve the problem that the position accuracy of the DPD algorithm decreases due to dispersed multi-array distribution and nonuniform noise power distribution caused by difference among array elements in passive localization systems. The covariance matrixes of the array data are calculated and the results are transmitted to the process center. Then, the power of the nonuniform noise and the position of the targets are co-estimated simultaneously using the maximum likelihood method with iteration, and the converged result is taken as the target position estimation, so that the effect of the nonuniform noise is reduced. The alternative projection method is utilized to lower the algorithm complexity when multi targets exist. Compared with the traditional method, the UN-ML-DPD algorithm can improve the position accuracy under low signal-to-noise ratio (SNR). Simulation results show that the estimation error is lower than 15 km for SNR is -15 dB, and the accuracy of the position estimation is increased by 15% compared with the DPD method. The noise covariance matrix is well estimated, and the estimation error is less than 3.5 W when the standard power of the noise is lower than 30 W. Moreover, the position accuracy approaches the CRLB when the SNR are high.

passive localization; multi-array; nonuniform noise; direct position determination; maximum likelihood estimation

2015-01-09。

黄志英(1987—),男,硕士生;吴江(通信作者),男,副教授,硕士生导师。

国家自然科学基金资助项目(61201381)。

时间:2015-07-23

10.7652/xjtuxb201510022

TN911.7

A

0253-987X(2015)10-0136-07

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150723.0922.010.html