误码条件下的LDPC码盲识别算法

包昕,周磊砢,何可,王桂良,游凌

(盲信号处理重点实验室, 610041, 成都)



误码条件下的LDPC码盲识别算法

包昕,周磊砢,何可,王桂良,游凌

(盲信号处理重点实验室, 610041, 成都)

为解决误码条件下信道编码校验矩阵难以逆向重建的问题,提出了一种新颖的LDPC码盲识别算法,简称迭代筛选(IS)算法。首先,由被截获数据构造含错矩阵,通过实施列消元运算获取其对偶向量;接着,利用校验向量判定准则从对偶向量中筛选出LDPC码的有效校验向量;进而再对被截获数据中的含错码组进行辨识和剔除;迭代进行以上操作,不断提高被截获数据内无误码码组的比例,直至将原问题退化为无误码时的简单场景;最终使用渐进行变换算法,实现LDPC码校验矩阵的稀疏化。仿真和实测均显示,IS算法对于802.16e、802.11n、DVB-S2、GJB7296、GB20600等公开标准均有效,能够在误码率不高于10-4条件下的非合作场合实现LDPC码的盲识别,LDPC码校验矩阵获得了完整重建。

变换信道编码;LDPC码;盲识别;误码率

信道编码是一种保证通信可靠性的技术手段,是现代通信系统的重要组成部分。在非合作条件下,展开对信道编码的有效识别,具有重要的军事意义和情报价值。信道编码盲识别问题力求解决,如何通过含噪序列R重建编码C,而LDPC码盲识别问题是其子问题。

对于传统信道编码,Valembois证明了其盲识别问题是一种NP完全问题[1],基于此结论,相关研究成果均将快速搜索次优解作为解决问题的途径。较有代表性的有:Cluzeau提出了一种有效的对偶码组搜索策略[2],该策略借鉴了Canteaut提出的最小码重搜索算法[3]和Gallager提出的置信度传播概率译码思想[4];游凌利用Walsh-Hadamard变换,提高了误码条件下短码校验关系的穷举速度[5];陆佩忠基于Grönber基理论,将卷积码识别问题等价为线性移位寄存器的综合[6]。然而,以上方法均不适用于LDPC码识别问题。

LDPC码是一种由校验矩阵定义的分组码,具有码长长、校验矩阵稀疏、性能逼近香农限的特点。自1995年LDPC码被重新发现以来,人们围绕其构造、编码、译码方法展开了深入的研究,当前已应用于卫星、深空、移动、无线、光纤在内的各种通信系统,成为最具潜力的信道编码解决方案。

然而,针对LDPC码盲识别问题的研究成果极为有限。Cluzeau证明,足够多的LDPC码码组是确保多项式时间内重建LDPC码的充要条件[7]。文献[8-9]通过计算后验概率对数似然比(LLR),将实数域上的软解调序列与LDPC码的校验关系联系在一起。文献[10]在此基础上,形成闭集识别算法。遗憾的是,这些研究成果远不能满足非合作背景下LDPC码盲识别的现实需求。

本文着重解决误码条件下的LDPC码开集识别问题,尝试综合利用列消元运算、校验向量判定准则及渐进行变换等方法,以发现正确校验向量和剔除含误码码组作为手段,最终将原问题成功退化为无误码条件下的稀疏校验矩阵重建问题,实现了误码条件下的LDPC码盲识别。

1 问题描述与分析

LDPC码盲识别的最终目标,是实现稀疏校验矩阵的正确重建。码长n和码组起点的正确识别,是该目标得以实现的基础,文献[11-12]以矩阵二元域上的秩作为统计判决量,重点研究了此问题。考虑到该问题的复杂性和独立性,本文为简化讨论和分析,假设码长和码组的起点已知。

在无误码情况下,对LDPC码接收序列进行高斯消元,总能够获取码字空间的一组基,即生成矩阵G,进而方便地获取至少一个非稀疏校验矩阵Hd。在此基础上,利用足够多次数的线性行变换运算,可最终实现稀疏校验矩阵的正确重建。图1给出了无误码条件下的盲识别流程。

图1 无误码条件下的校验矩阵重建

在误码条件下,由于高斯消元法对误码极为敏感,此时已不可能通过使用高斯消元运算获取LDPC码码字空间的基。因此,需寻找新的解决思路。本文将稀疏校验矩阵的重建问题分解为3个相对独立的子问题:①获得含错码组的正交向量;②对码字空间C的有效校验向量进行辨识;③稀疏化有效校验向量。其中,问题2将在第3节中详细讨论,问题3的解决方案将在其余文章中专门讨论。问题1是本文重建问题的核心。一种朴素的正交向量发现思想是,通过穷举n维空间内的所有2n组向量,搜索满足正交性的校验向量。但是,无论是使用Canteaut方法、Walsh-Hadamard变换或者是借助巨型机,该思想都不现实。本文引入的k阶列消元运算,将方便地解决问题1。

图2给出了本文所提出的解决方案:首先,使用k阶列消元运算,获取含误码码组的大量正交向量,称作疑似校验向量;接着,利用统计判定准则,从正交向量中遴选出码字空间的有效校验向量;然后,利用以上有效校验向量,辨识和剔除接收序列中被发现的含误码码组;迭代进行以上一系列操作,不断提高接收序列内无误码码组的比例,只要待识别码组数量足够多,经过有限次迭代,总能找到足够多的有效校验向量,同时剔除所有含误码码组。此时,误码条件下的盲识别问题,已退化为前述无误码时的情况。

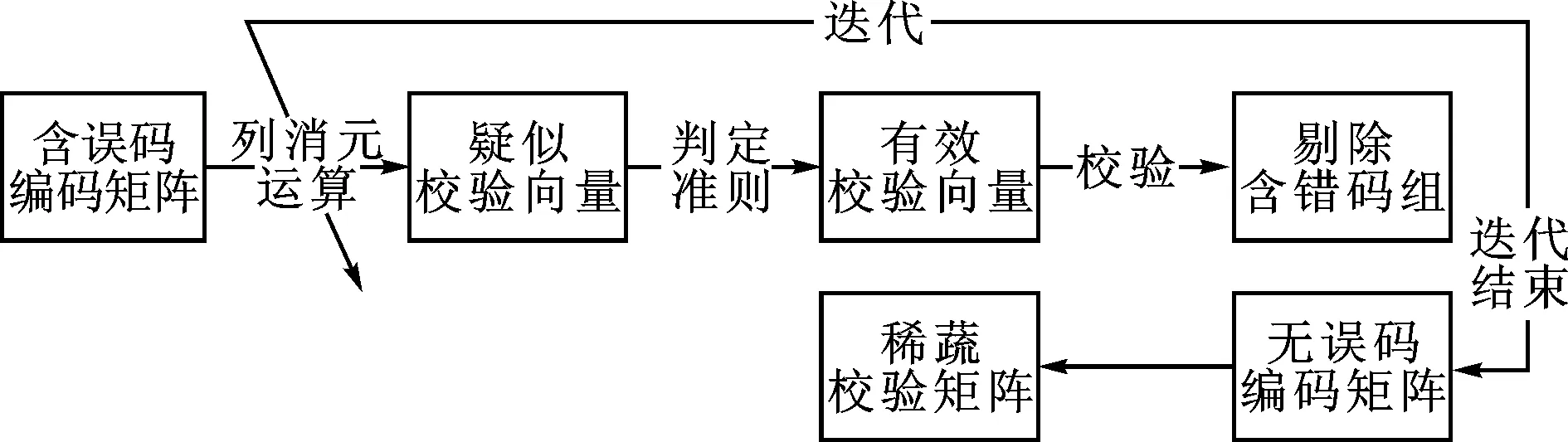
图2 误码条件下的校验矩阵重建方案框图

至此,本文给出了一种误码条件下的LDPC码有效盲识别方法,后续章节将对具体实现技术展开讨论。

2 k阶列消元运算

k阶列消元运算的目标,是将任意给定的二元矩阵M,通过k步操作,变换为形如下式的下阶梯型矩阵

(1)

并得到M的对偶矩阵Θ。

设M经i-1步运算后记为M(i-1),可构造形如下式的矩阵

(2)

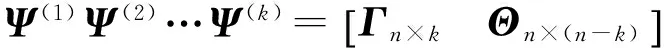
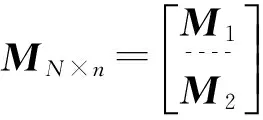
(1)无误码的情况。设MN×n=mG,其中m为N×k维信息矩阵,G为C的生成矩阵,易得

(3)

若对M进行k阶列消元运算,必然存在矩阵Θn×(n-k),使得0=M1Θ,即

(4)

因此,存在矩阵Θ,使得MΘ为全0阵。

(2)存在误码的情况。设MN×n=mG+EN×n,E为错误图样。易得

(5)

对M进行k阶列消元运算,必然存在矩阵Θn×(n-k),使得0=M1Θ,即

(6)

因此

(7)

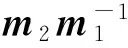
图3给出了对M进行k阶列消元后的变化结果,其中M由100组(40,25)分组码组成。可见,经k阶列消元运算后,当M无误码时,MΘ为全0阵;当M存在误码时,MΘ前k行为全0阵,余下N-k行存在非零元素。由此,k阶列消元运算一方面可用于快速获取编码矩阵M的正交矩阵,另一方面可方便地判定矩阵M是否存在误码。

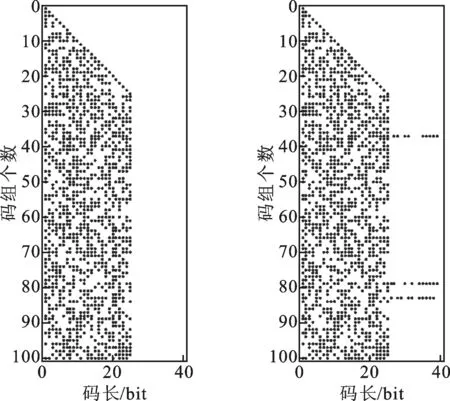
(a)无误码 (b)误码率为10-4图3 对某(40,25)分组码的列消元处理结果

3 疑似校验向量的判定

Gallager指出,若n维二元向量中元素为1的概率记做p,则该向量中存在偶数个1的概率为[1+(1-2p)n]/2[4]。Chabot给出了如下结论[12]。

定理1 令向量p,q∈R,且w表示q中非零元素个数,则p、q正交概率pr(〈p,q〉=0)为

(8)

式中:R⊥表示空间R的对偶空间;pb为p中非零元素的出现概率。当p表示校验向量h、q表示含噪接收向量r时,该定理可用于判定r是否属于码字空间C;同理,当p表示编码向量c、q表示任意向量h时,该定理可用于判定h是否属于校验空间C⊥。

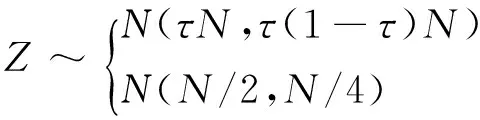
(9)

式中:τ=[1-(1-2pe)w(h)]/2。

4 矩阵的稀疏化

(n,k)分组码码字空间C由2k个码字c组成,可看作由2k个信息向量m通过生成矩阵G的线性表出。若G由k个n维线性无关向量组成,则G称作码字空间C的一组基;相似地,若校验矩阵H由n-k个n维线性无关向量组成,由于H与(n,k)分组码的所有2k个码字c正交,则由H张成的空间必定与码字空间C正交,该空间称为C的校验空间C⊥,H称为C⊥的一组基。因此,恢复(n,k)分组码的生成矩阵G,就是寻找码字空间C的某组基;而恢复校验矩阵H,就是寻找码字校验空间C⊥的某组基。

渐近行变换(gradual row transform,GRT),是一种以非稀疏检验矩阵行作为优化对象的矩阵稀疏化算法,能够有效实现无误码条件下LDPC码的矩阵重建。

5 误码条件下的盲识别算法

5.1 算法描述

前述章节依次解决了对偶向量的获取、有效校验向量的辨识、矩阵的稀疏化3个问题。这些问题的综合,即为误码条件下的LDPC码盲识别问题。将N个接收码组ri,i=1,2,…,N逐行排列形成矩阵M,则盲识别算法步骤如下。

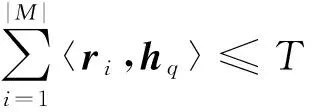
(2)采用GRT算法,获得如下稀疏矩阵: 对M进行高斯消元获得G; 对G使用GTT算法获得M。

表1给出了算法复杂度分析。可见算法的计算复杂度最多为O≈2Nn3+OGRT。

表1 算法复杂度分析

注:N′表示一次迭代中M的码组个数;l表示一次迭代获取的有效校验向量个数;OGRT表示GRT运算级计算量。

5.2 算法测试

当前,LDPC码已应用于卫星、深空、移动、无线、光纤在内的各种通信系统。本节仅以无线城域网IEEE 802.16e标准[13]为例展开算法测试。

例1 给定(576,288)LDPC码,误码率pe=10-4时,设定码组个数N=3k=864。测试显示,经4次迭代运算,可获得807组无误码码组c和528组有效校验向量h。对以上无误码码组采用GRT算法,所获得的非稀疏矩阵及重建后的稀疏矩阵分别如图4a、图4b所示,经与真实校验矩阵(图4c)比对,可确认稀疏校检矩阵H获得了正确重建。

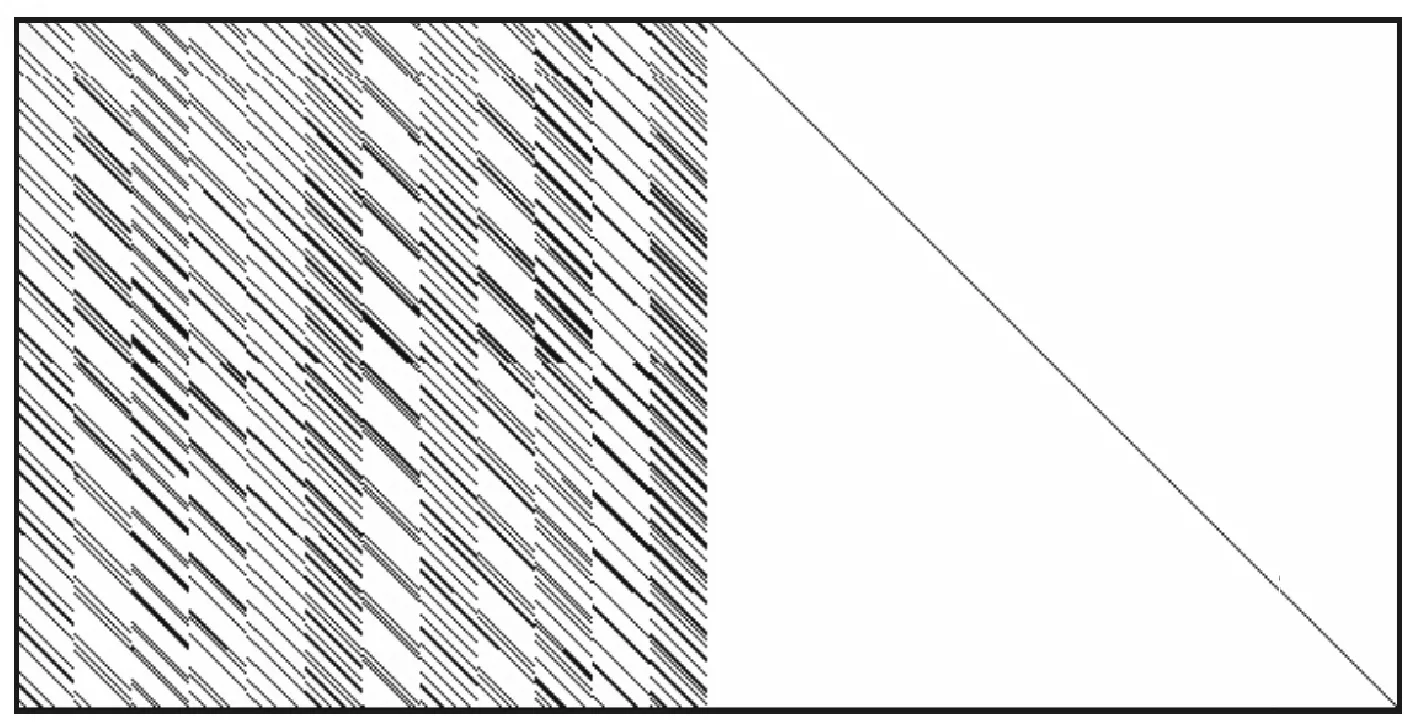
(a)非稀疏校验矩阵

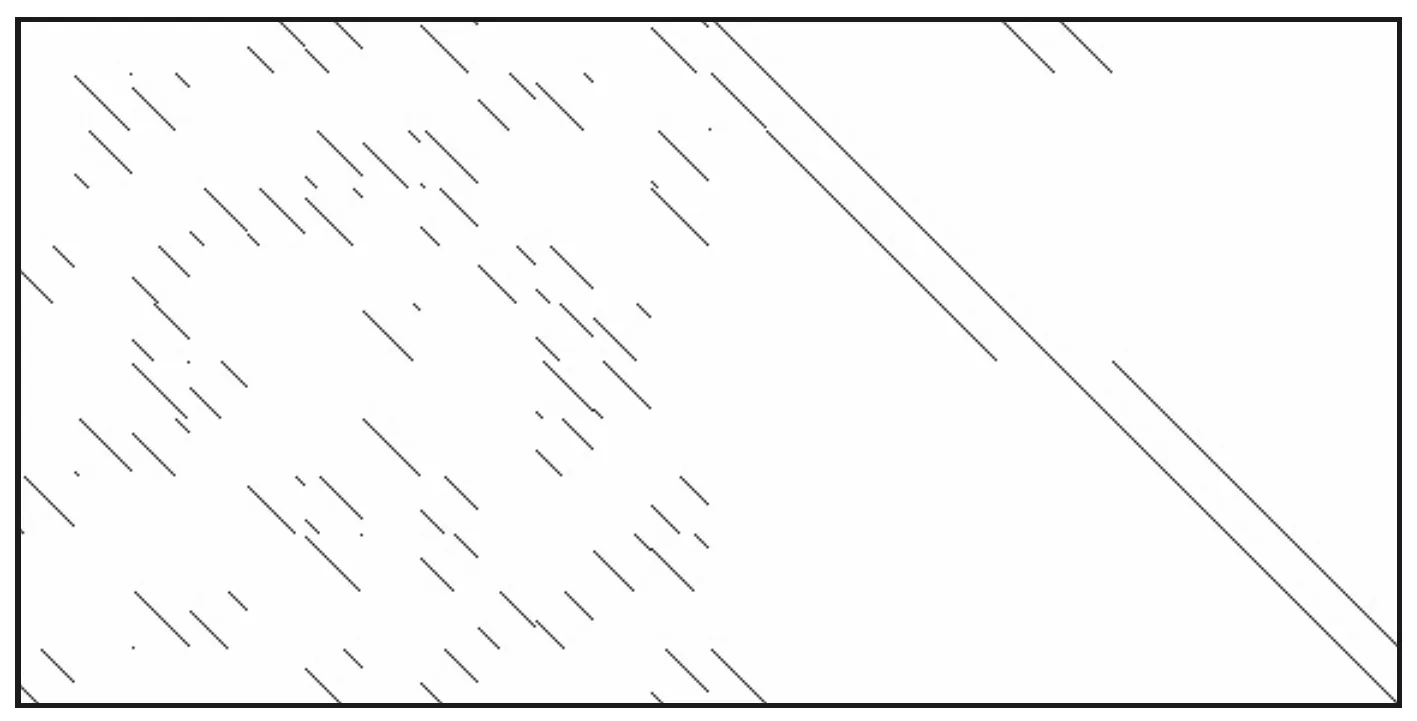
(b)重建后的稀疏校验矩阵

(c)真实校验矩阵图4 例1中(576,288)LDPC码仿真情况

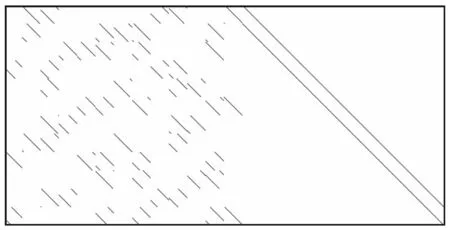
例2 保持码组数N=864不变,将误码率提高到pe=3×10-4。此时,经6次迭代后,共获得750组无误码码组c和354组有效校验向量h。经GRT算法处理后,所重建的矩阵如图5所示。

经统计,该矩阵包含非零元素1 852个、4环1个、6环46个,而在图4c所示的真实矩阵中,以上参数分别为1 824、0和24。可见,测试中所获取的354组有效校验向量h还未能完整张成(576,288)编码的对偶空间,校验矩阵重建失败。

图5 例2中(576,288)LDPC码仿真情况

例3 保持误码率pe=3×10-4,将码组数提高到N=5k=1 440。经7次迭代后,共获得1 188组无误码码组c和1 152组有效校验向量h,稀疏校验矩阵H再次获得重建。

表2给出了此次测试时,迭代过程的中间变量。可见,首次迭代所获取的有效校验向量可以极少,随着迭代的进行,越来越多的有效校验向量h将被发现,越来越多的误码码组将被剔除,最终,含误码码组比例由最初的16.53%收敛至0%,同时有效校验向量个数正好等于288组。

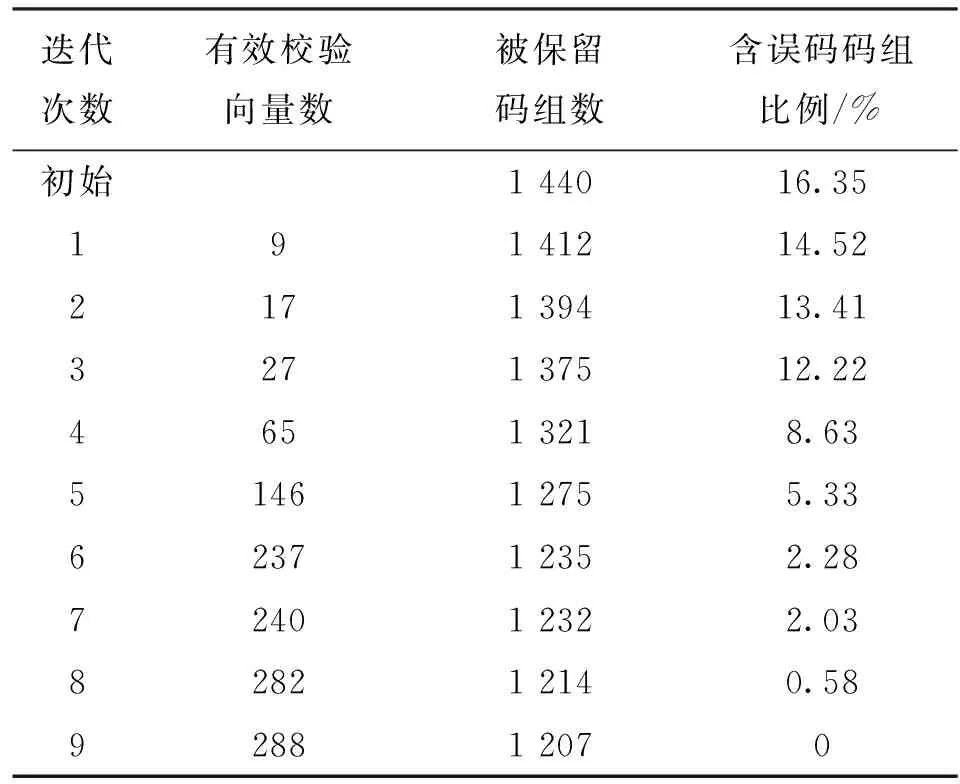
表2 例2中(576,288)LDPC码的仿真中间变量

例4 扩大码长,选取(1 152,864)LDPC码,测试参数为pe=10-4,N=10k=8 640。经3次迭代运算,共获得7 590组无误码码组c和4 608组有效校验向量h。校验矩阵重建结果如图6所示。

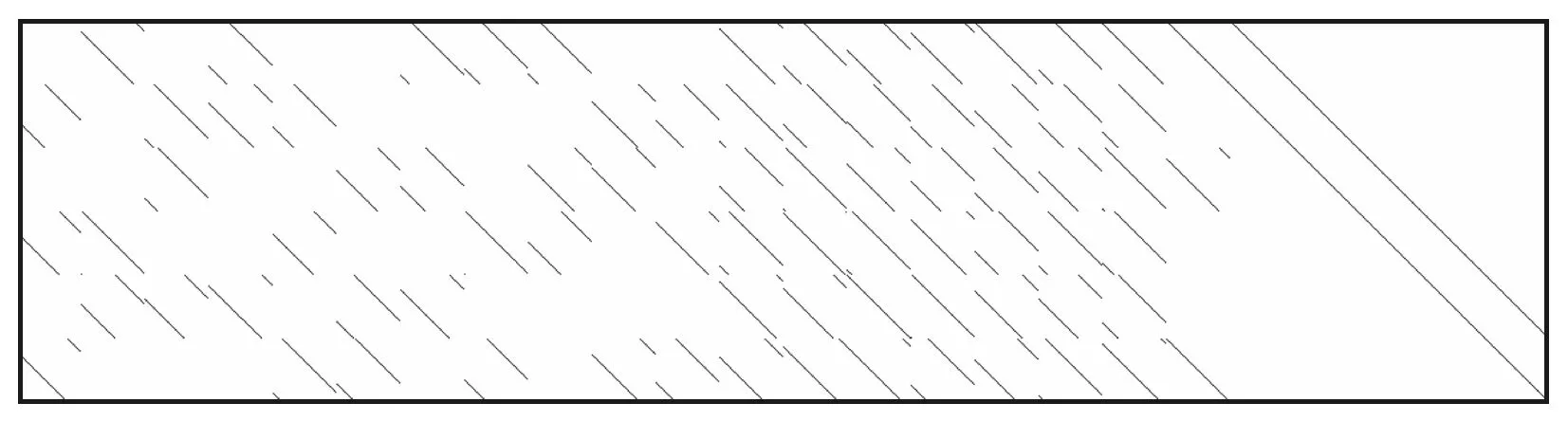
图6 例4中(1 152,864)LDPC仿真情况

本文还对DVB-S2[14]、IEEE 802.11n[15]、GJB 7296及GB 20600[16]等标准/协议进行了测试。测试结果显示,本文算法具备较好的通用性。

5.3 讨论

由仿真可以发现,通过增加码组数量N,在一定层度上可提高算法的容错性能。本算法成功的关键是能否通过若干次k阶列消元运算,凑齐足够多的无误码码组。一方面,参与算法的N个码组中应当确实存在至少k个无误码码组,即

(10)

此为N的一个松弛下限。另一方面,即使N个码组中存在k个无误码码组,能否将其发现也存在不确定性。由于一次k阶列消元运算仅能获取子矩阵Mi的n-k个正交向量,而其中并不保证存在编码C的有效校验向量h。将一次k阶列消元运算中有效校验向量h的产生概率称为发现概率ph。

(11)

特别地,当ph→0时,N→∞,算法等价于失效。

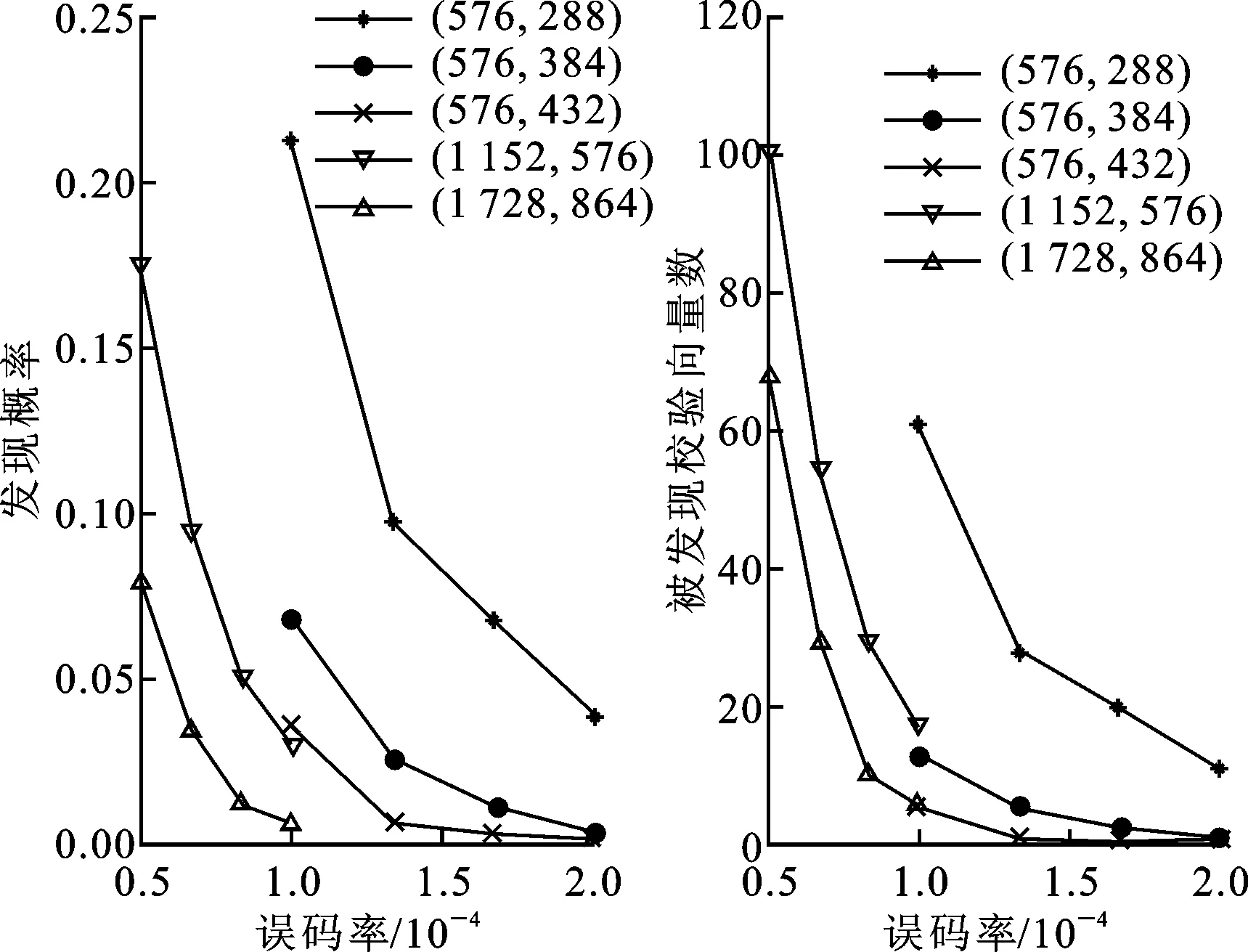
(a)发现概率 (b)被发现校验向量数图7 不同编码时误码率与发现概率和被发现校验向量数关系的仿真曲线

至此,分别得出了算法有效时所需码组数量N与误码率pe的两种表述方法,为算法复杂度与容错性能的折中问题提供了一定依据。

6 结 论

针对误码条件下的LDPC码开集盲识别问题,本文提出了一种有效的解决方案。测试结果显示,算法适用于包括802.16e、802.11n、DVB-S2、GJB7296、GB20600在内的多种LDPC标准/协议,实用性强。本文算法通过将原本棘手的研究对象分解为3个相对独立的子问题,综合利用k阶列消元运算、基于统计学原理的校验向量判定准则和渐进行变换算法,成功地将问题退化为无误码条件下的LDPC码盲识别问题,最终实现了LDPC码稀疏校验矩阵的完整重建。特别是本文得出了利用增加码组数量换取算法容错性能的结论,具有一定的现实指导意义。

[1] VALEMBOIS A. Detection and recognition of a binary linear code [J]. Discrete Applied Mathematics, 2001, 111(1): 199-218.

[2] CLUZEAU M. Block code reconstruction using iterative decoding techniques [C]∥Proceedings of 2006 IEEE International Symposium on Information Theory. Piscataway NJ, USA: IEEE, 2006: 2269-2273.

[3] CANTEAUT A, CHABAUD F. A new algorithm for finding minimum-weight words in a linear code: application to McEliece’s cryptosystem and to narrow-sense BCH codes of length 511 [J]. IEEE Transactions on Information Theory, 1998, 44(1): 367-378.

[4] GALLAGER R G. Low-density parity-check codes [J]. IEEE Transactions on Information Theory, 1962, 8(1): 21-28.

[5] 游凌, 朱中梁. Walsh函数在解二元域方程组上的应用 [J]. 信号处理, 2000, 16(S1): 27-30. YOU Ling, ZHU Zhongliang. The application of Walsh function in resolving of GF(2) equations [J]. Signal Processing, 2000, 16(S1): 27-30.

[6] 陆佩忠. 删除卷积码的盲识别 [J]. 中国科学学: E辑, 2005, 35(2): 173-185. LU Peizhong. Blind recognition of punctured convolutional codes [J]. Science in China: Series E, 2005, 35(2): 173-185.

[7] CLUZEAU M, TILLICH J. On the code reverse engineering problem [C]∥Proceedings of IEEE International Symposium on Information Theory. Piscataway, NJ, USA: IEEE, 2008: 634-638.

[8] 于沛东. 一种利用软判决的信道编码识别新算法 [J]. 电子学报, 2013(2): 301-306. YU Peidong. A novel algorithm for channel coding recognition using soft decision [J]. Acta Electronica Sinica, 2013(2): 301-306.

[9] XIA T. Novel blind identification of LDPC codes using average LLR of syndrome: a posteriori probability

[J]. IEEE Transactions on Signal Processing, 2014, 62: 632-640.

[10]包昕. 基于软解调序列的LDPC码闭集识别方法 [J]. 电讯技术, 2015, 55(1): 55-60. BAO Xin. A finite set recognition algorithm of LDPC coding by using soft-demodulation sequence [J]. Telecommunication Engineering, 2015, 55(1): 55-60.

[11]BARBIER J. SICOT G, HOUCKE S. Algebraic approach for the reconstruction of linear and convolutional error correcting codes [J]. Proceedings of World Academy of Science Engineering & Technology, 2006, 2(3): 113-118.

[12]CHABOT C. Recognition of a code in a noisy environment [C]∥Proceedings of IEEE International Symposium on Information Theory. Piscataway, NJ, USA: IEEE, 2007: 2211-2215.

[13]LAN/MAN Standards Committee of IEEE Computer Society. Draft IEEE Standard for Local and metropolitan area networks: Part 16 Air interface for fixed and mobile broadband wireless access systems amendment for physical and medium access control layers for combined fixed and mobile operation in licensed bands [S]. New York, USA: IEEE Standards Activities Department, 2005.

[14]European Broadcasting Union. Digital video broadcasting (DVB): second generation framing structure, channel coding and modulation systems for Broadcasting, interactive services, news gathering and other broadband satellite applications [S]. Geneva, Switzerland: European Telecommunications Standards Institute, 2006.

[15]LAN/MAN Standards Committee of IEEE Computer Society. IEEE standard for information technology telecommunications and information exchange between systems: local and metropolitan area networks specific requirements: Part 11 Wireless LAN medium access control (MAC) and physical layer (PHY) specifications [S]. New York, USA: IEEE Standards Activities Department, 2009.

[16]中国国家标准化管理委员会. 数字电视地面广播传输系统帧结构, 信道编码和调制 [S]. 北京: 中国标准出版社, 2007.

(编辑 刘杨)

A Recognition Algorithm for LDPC Codes of Blind in a Noisy Environment

BAO Xin,ZHOU Leike,HE Ke,WANG Guiliang,YOU Ling

(Science and Technology on Blind Signals Processing Laboratory, Chengdu 610041, China)

A novel recognition algorithm (called iterative screening, IS) for LDPC codes of blind is proposed to solve the problem that the parity-check matrix of Channel Coding is hard to reconstruct in a noisy environment. A matrix with the intercepted data is constructed, and then dual vectors of the matrix are obtained by using column elimination operation. Effective parity-check vectors of the dual-space of the LDPC code are selected and error code blocks are recognized and deleted from the intercepted data. These steps are iteratively carried out until the original problem is reduced to a simple problem, i.e., blind recognition of some error-free codes. The sparse parity check matrix is finally obtained by using Gradual Row Transformation. Simulation and experimental results show that the IS algorithm can apply to most LDPC standards, such as 802.16e, 802.11n, DVB-S2, GJB7296 and GB20600. It is able to be used in the non-cooperative context with the bit error rate less than 10-4, and reconstructs the sparse parity check matrix of LDPC codes.

channel coding; LDPC codes; blind recognition; error bit rate

2015-04-23。

包昕(1986—),男,博士生;游凌(通信作者),男,高级工程师,博士生导师。

国家自然科学基金资助项目(61172140)。

时间:2015-10-03

10.7652/xjtuxb201512009

TN911.22

A

0253-987X(2015)12-0053-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151003.1918.004.html