利用表面肌电信号的下肢动态关节力矩预测模型

陈江城,张小栋,李睿,石强勇,王贺

(西安交通大学现代设计及转子轴承系统教育部重点实验室, 710049, 西安)



利用表面肌电信号的下肢动态关节力矩预测模型

陈江城,张小栋,李睿,石强勇,王贺

(西安交通大学现代设计及转子轴承系统教育部重点实验室, 710049, 西安)

为实现表面肌电信号的下肢关节力矩动态解码,建立了从表面肌电信号到关节力矩输出的人体下肢运动系统正向生物力学模型。首先,从幅值和频率两个角度建立表面肌电信号到骨骼肌激活程度模型;其次,根据肌丝滑移理论,构建反映骨骼肌生理结构和微观力学特性的肌肉力模型,同时确定活动肌肉拉力线方向及力作用点位移矢量,将骨骼肌力转换到关节力矩;最后,以牛顿-欧拉逆动力学方法获得关节力矩作为准确值,给出正向生物力学模型参数动态标定方法。在模型基础上,对4名对象进行随意步态下膝关节屈伸动态力矩预测试验,结果表明:所建模型对步态行走下的膝关节动态关节力矩具有很好的动态跟踪性能,最大绝对误差为(11.0±1.32) N·m,平均残差为(4.43±0.698) N·m,预测值与准确值之间的平均线性相关系数为0.927±0.042,验证了该方法的正确性和有效性;可为康复训练机器人人机协同过程中的力学交互模式研究提供接口。

表面肌电信号;关节力矩预测;肌肉模型;正向生物力学

运动训练对中风偏瘫患者的运动功能恢复十分重要,康复训练机器人具有比人工医疗师辅助训练更多的优点而被研究者和康复工作者所认可,目前世界上典型的下肢康复训练机器人有LOPES、LOKOMAT、Gait Trainer和Haptic Walker等[1]。康复训练过程一般分为被动阶段和主动阶段,主动阶段注重患者的主动参与和自身能力,选择性地给患者提供助力[2-3]。实际上,康复机器人辅助的根本作用是,在患者自身力量无法提供目标运动所需力的时候,给患者额外提供部分需要的力,通过训练逐渐摆脱机器人的帮助,达到人进机退,同时应保证人、机力交互的柔顺性[4]。因此,康复机器人需要对患者实际运动能力进行实时感知,但是目前由于缺少对患者运动能力的直接感知手段,从力交互机理出发设计的康复控制策略很少,制约康复机器人的进一步提高。

骨骼肌是人体运动的主要动力源,在神经系统调控下收缩,牵引骨骼和关节运动,因此通过运动中骨骼肌收缩力检测可以感知人体的运动能力。目前,直接测量体内肌肉力大小是不现实的,表面肌电(sEMG)蕴含肌肉活动强度、活动时间等信息,成为体表无创检测肌肉活动的重要方法,被广泛用于康复领域。文献[5]将表面肌电信号的强度与关节力矩等效成一阶线性关系,通过表面肌电信号估计关节力矩,并控制助行外骨骼机器人,增强了穿戴者的行走能力。文献[6]通过Hill肌肉模型建立表面肌电信号与关节力矩的关系,用于控制外骨骼机器人。文献[7]通过收集特定肌肉上的肌电信号并进行处理,当被处理的信号超过一定阈值时触发辅助,作为给患者的奖励,相同的肌电生物反馈方法也被用于上肢的康复训练[8-9]。另外,文献[10]通过神经网络学习,建立了表面肌电信号与关节力矩的关系,用于上肢假肢控制;文献[11-12]都基于Hill肌肉模型建立了幅值大小到关节力矩的映射模型。

综上可以看出,通过肌电感知肌肉力和关节力矩是一种可行的方法。然而研究表明,产生相同的肌肉力在不同的运动任务下肌电活动模式是不一样的,而且不是简单的线性关系,若要保证预测模型的精度及在任意运动下都有效,所建立的模型必须能反映运动系统的解剖结构和生理特点[11]。Hill模型是在离体肌肉实验基础上提出的[13],没有考虑肌肉收缩的微观特性,也不能描述活体肌肉完整生物力学过程。文献[14]基于肌丝滑移理论,从微观角度研究肌肉的力学特性,从频率角度分析表面肌电信号与骨骼肌力之间的关系,重点讨论了基于表面肌电的肌力预测结果,没有对关节力矩的预测进行研究。

本文以提高下肢康复机器人的运动感知能力为目标,考虑下肢系统运动生物力学模型的完整性和动态力矩预测的准确性,对骨骼肌生物电调控(激励)、收缩力学模型以及肌肉力到关节力矩等过程进行深入研究,从运动机理出发,构建了下肢运动系统正向生物力学全过程模型,实现了下肢运动力学信息的表面肌电信号动态解码,为下肢康复机器人力交互机理及辅助控制策略研究提供合适的人机交互接口。

1 正向生物力学模型

建立正向生物力学模型的最终目标是:通过输入原始表面肌电信号和关节运动学数据得到关节力矩的大小,且使模型能够适用于较宽的运动任务(除发生痉挛等意外)和任意下肢关节。人体下肢运动系统主要包括神经、肌肉和骨骼关节3个部分,分别发挥控制、驱动和执行的作用。根据其力学过程,本文分别建立肌肉生物电激活模型、肌肉收缩力学模型及肌肉功能模型,3者按照力学关系联合形成完整的正向生物力学模型,如图1所示。其中,肌肉生物电激活模型的作用是将表面肌电信号sEMG表征为肌肉激活程度a(t),肌肉收缩生物力学模型描述肌肉在激活程度a(t)下的输出力Fm(t)的情况,肌肉功能模型作用是将相关联肌肉力合成得到关节力矩Tj(t)输出。

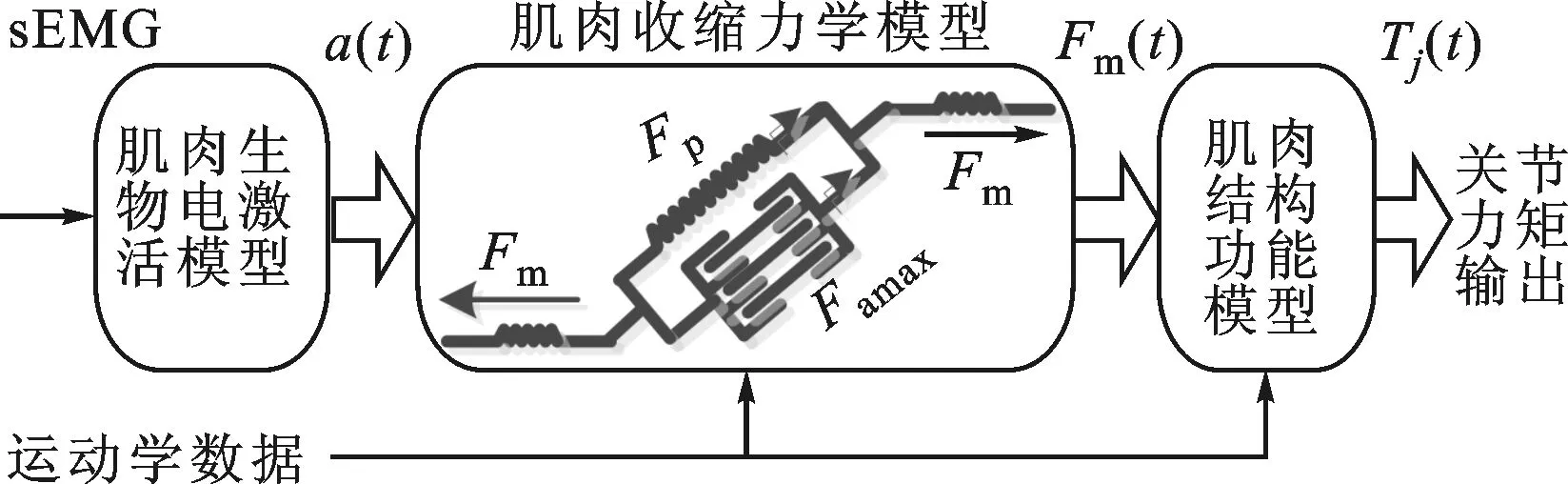
图1 正向生物力学模型建立过程

1.1 肌肉生物电激活模型

人体骨骼肌由大量肌纤维组成,肌纤维的活动受到神经系统控制,一个神经元和受其支配的所有肌纤维构成一个运动单位。肌纤维的收缩是集力学、生理学和生物化学的一个复杂过程。在神经冲动的激励下,肌细胞膜激发动作电位,一方面叠加形成皮肤表面肌电信号,另一方面兴奋整个细胞,经过兴奋收缩耦联引起肌丝滑移。因此,表面肌电信号表征了肌肉的激活强度,其按照以下3个步骤形成肌肉生物电激活模型。

(1)对于单根肌纤维,当动作电位幅值超过门限值,会引起肌浆网Ca2+通道开启,使Ca2+进入肌浆,当动作电位幅值低于门限值,Ca2+又迅速回流,肌浆内的Ca2+与肌纤维中的肌钙蛋白作用引起肌丝滑移,Ca2+浓度决定着肌纤维收缩强度。肌纤维激发动作电位存在“全或无”的特点,即只要激发,其波形幅值变化固定,所以肌浆内的Ca2+浓度是通过动作电位发放率调控的。文献[15]从肌纤维的生理结构和运动机理出发,建立了肌浆内平均Ca2+浓度μ与动作电位发放率的数学模型,并通过Sigmoid函数拟合

(1)

式中:fa为动作电位发放率;a1、b1和c1为拟合系数。另外,μ与肌纤维激活程度β的关系可以表示为

(2)

式中:K1=8.72,表示Ca2+与肌钙蛋白弱作用时两者分离速率与结合速率之比;K2=0.194,表示Ca2+与肌钙蛋白强作用时两者分离速率与结合速率之比。

以往研究发现,肌纤维的动作电位发放率在8～50 Hz之间[16],而表面肌电信号的有效频率范围是在20～500 Hz之间。本文通过线性模型建立两者之间的映射关系,以表面肌电信号短时傅里叶变换后得到中值频率fm表示表面肌电信号频率,线性变换得到肌纤维动作电位发放率,即

(3)

式中:fi(t)为Ai(t)时刻短时傅里叶变换的各频率;Ai(t)为各频率点对应的幅值;N为频率点数,由频率分辨率,即短时傅里叶变换所用窗函数宽度决定。至此,式(1)～式(3)描述了表面肌电信号频率与单根肌纤维激活程度的关系。

(2)对于整个肌肉,其激活程度还与肌纤维的募集数量有关,肌纤维募集越多,就有更多的肌膜动作电位叠加形成表面肌电信号,因此可用表面肌电信号的幅值反映肌纤维募集数量。对于原始表面肌电信号,通过零滞后的四阶巴斯沃特滤波器进行滤波,以达到消除运动伪迹的目的,截止频率为20 Hz。在此基础上,进行全波整流和4 Hz低通滤波得到时域信号R(t),表示表面肌电信号活动强度。用相同的方法对每块肌肉在最大主动收缩力下测得的表面肌电信号进行处理,得到时域信号RMVC(t),取其中最大值作为标准,对所有试验下处理后的肌电信号进行归一化处理,转化为肌纤维募集程度,即

(4)

(3)任意骨骼肌的激活程度可以表示为肌纤维激活程度与肌纤维募集程度的乘积

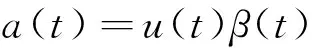
(5)

利用上述模型,由某对象股直肌表面肌电信号计算肌肉激活程度,如图2所示。从图可知,同时考虑幅值与频率两个因素时获得的肌肉激活程度a与单独考虑幅值时的肌肉激活程度u相比,变化趋势微小,但是幅值上变化较为明显。激活程度的改变将影响后续模型参数的准确性。

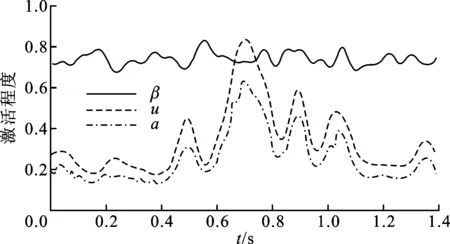
图2 肌肉激活程度变化曲线

1.2 肌肉收缩力学模型

目前,对肌肉生物力学研究多数是在Hill提出的肌肉力学模型基础上进行的,其肌肉力方程为

(6)

式中:Fmmax为肌肉最大等长收缩力;l为肌肉纤维长度;v为肌肉收缩速度;f(l)、f(v)和fp(l)为归一化的肌纤维力学特性曲线,是通过离体实验测量得到的,没有考虑微观特性,因此无法有效反映活体肌肉生理参数对生物力学的影响。

从微观上看,骨骼肌收缩是由于大量肌球蛋白分子马达对细肌丝集体做功引起粗细肌丝相对滑移导致的。基于肌丝滑移理论,文献[17]提出了肌肉横桥动力学模型,推出了肌丝滑动速率方程和肌丝横截面上的主动力力学方程。文献[18-19]通过二态布朗棘轮模型及统计动力学方法,研究了分子马达的集体运行特性。文献[20]针对肌纤维结构特点和肌球蛋白马达运行机制,利用非平衡统计力学的方法,构建了肌节主动收缩力学模型,该模型可以用于定量讨论负载力、Ca2+及能量因子三磷酸腺苷浓度等对收缩力学特性的影响。

肌节是肌肉收缩最小功能单元,骨骼肌是由大量肌节串并联而成,而肌肉整体收缩力大小与肌节并联数目相关,任意骨骼肌的主动收缩力学模型可以表示为

(7)

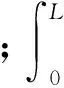
(8)

另外,根据文献[21]对肌节主动力和肌节长度关系的实验研究表明,主动力随着肌节长度增加先增后减,本文用高斯函数模拟粗细肌丝的重叠程度α,即

(9)

式中:lopti为肌肉最大等长收缩时肌肉纤维长度。

除主动收缩力外,肌肉组织本身还存在被动拉伸的特性,采用刚度阻尼模型表示为

(10)

式中:km表示肌肉刚度;γm为肌肉阻尼;lo为肌纤维初始长度;Δlm为肌肉伸长量。

因此,肌肉收缩力学模型为

Fm=Fa+Fp

(11)

从肌肉收缩力学模型可知,除激活程度a外,肌肉截面积Sm、最优长度lopti、刚度km及阻尼γm等结构和物理参数都影响肌肉收缩力的大小。

1.3 肌肉功能模型

根据肌肉结构及力学原理,肌肉收缩力在关节上产生的转动力矩为

T=r×Fcosφ

(12)

式中:r表示关节转动中心到力作用点的位移矢量;F表示肌肉力矢量;φ表示肌肉羽状角。因此,要将肌肉力转换到关节力矩的大小,需要进一步确定肌肉拉力线方向矢量I和位移矢量r。

肌肉附着点位置,包括起点、代起点、止点和代止点,是确定肌肉长度、肌肉伸缩速度、肌肉拉力线和肌肉力作用点的基础。文献[22]通过大量尸体标本检测确定人体下肢肌肉附着点位置和人体下肢骨形参数,并以3个关节中心为坐标基准点,建立骨盆、大腿、小腿局部坐标系,给出了用于计算活体肌肉附着点三维坐标的线性回归方程。本文基于文献[22]研究结论,给出下肢位姿动态变化过程中的肌肉拉力线和力位移矢量的确定方法,具体步骤如下。

第1步,利用光学运动捕捉系统记录人体下肢关键点的位置,确定髋、膝和踝关节中心的位置坐标。对于膝关节和踝关节,以关节内外侧标记点位置的中心作为关节中心。采用文献[23]提出的方法确定髋关节中心:首先,以两髂前上棘中心为基准点,根据左右髂前上棘和髂后上棘位置坐标,建立骨盆坐标系,如图3所示,其坐标轴方向确定方法如下

(13)

(14)

U=V×W

(15)

其次,计算髋关节中心在骨盆坐标系中的位置,并转换至全局坐标系下。同时,根据文献[24]给出的线性回归方程确定髋关节中心在骨盆坐标系中的位置,方程如下

(16)

式中:Pd代表骨盆深度,为两髂前上棘中点与两髂后上棘中点之间的距离,mm;Pw代表骨盆宽度,为两髂前上棘之间的距离,mm。

图3 骨盆坐标系及与髋关节中心的关系

第2步,从骨盆、大腿、小腿分别选择3个标记点,以关节中心为基准点建立各肢体的局部坐标系,然后根据文献[22]给出的肌肉附着点三维坐标计算线性回归方程,计算附着点在局部坐标系中的位置,同时通过坐标变换,将附着点位置转换到全局坐标系下表示。

第3步,利用肌肉附着点以及关节中心坐标,确定在全局坐标下的肌肉拉力线方向矢量和力位移矢量r,同时计算肌肉长度lm、肌肉纤维长度l以及肌肉伸缩速度v。

在确定所有肌肉力方向矢量和力相对于关节中心的位移矢量后,分别选出对下肢各关节运动起作用的肌肉,计算每块肌肉对关节的力矩贡献并相加,得到该关节力矩,即

(17)

式中:j代表关节;N代表作用于该关节上的肌肉数量;φi表示第i块肌肉的羽状角。

2 模型的标定

从建立的下肢运动系统正向生物力学模型看出,模型中包括了反映肌肉生理特性及结构的参数,不同肌肉具有不同的参数大小,如横截面积较大的肌肉并联更多的肌节,产生的最大肌肉力也更大。因此,在模型应用于具体对象之前,需要对模型参数进行调整,即模型标定。

2.1 模型标定原理

模型标定需要一个标准的参考值。考虑测量人体活体肌肉在关节上的作用力不现实,本文利用足底力(GRF)和运动学数据,通过牛顿-欧拉逆动力学方程[25]计算各关节的输出力矩Tjiv,并将其作为模型标定的参考值。

模型标定的目标是通过调整正向生物力学模型参数,最终寻找一组合适的参数值,使模型输出的关节力矩Tj与标准参考值无限接近。本文采用模型参数优化算法实现这一目标,并定义优化目标函数如下

(18)

式中:n为采样点数。整个模型的标定过程如图4所示。

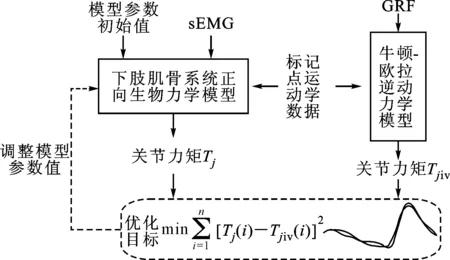
图4 模型标定过程

另外,为了使标定后模型能够适用于较宽的运动任务条件,优化函数中所选取的样本应尽可能涵盖复杂的运动情况,当然这也会增加模型参数寻找的时间。鉴于本文的目的是为康复机器人提供患者运动能力感知的功能,而康复的主要运动训练是步态行走,文中利用不同步行速度下的若干步态周期数据样本对模型参数进行标定,使标定后模型能够完成步态行走下的关节力矩准确预测。

2.2 模型参数的优化算法

为了实现目标函数的最小化,采用遗传优化算法寻找模型的最优参数值。模型中优化的参数包括肌肉收缩力学模型中的高斯函数标准差σ、肌肉最大力Famax、最优长度lopti以及刚度km和阻尼γm。对于肌肉的羽状角φ,文献[11]研究表明其值变化范围很小,因此本文采用该文献提供的羽状角数据,不对其进行优化。

在对模型参数进行优化时,初始种群的每个个体代表模型参数的一组初始值,进化方向为使目标函数值减小。另外,本文采用文献[26]提供的最大肌肉力和肌肉最优长度作为参考初始值,优化范围分别被约束在初始值上下±50%和±20%之间。这样一方面减小了优化搜索空间,加快优化速度,另一方面也能防止大幅度偏离实际情况而与解剖学知识不符的参数值出现。

3 膝关节动态力矩预测试验

为了验证模型的可靠性和有效性,选取4名男性对象A、B、C和D(平均年龄(29±5.5)岁,平均身高(172±4.3) cm,平均体质量(63.9±5.0) kg)进行生物力学模型标定和随意步态下的膝关节屈伸动态力矩预测试验。根据生理学先验知识,确定10块对膝关节运动有贡献的主要肌肉,分别是半膜肌(SM)、股二头肌长头(BFL)、股二头肌短头(BFS)、股内侧肌(VM)、股外侧肌(VL)、股直肌(RF)、腓肠肌内侧(MG)、腓肠肌外侧(LG)、阔筋膜张肌(TFL)和缝匠肌(SR)。实验中,所有受试者完成多种步速(约0.8、1.0和1.2 m/s)行走,记录相应的步态数据,试验设备场景如图5所示。下肢运动学数据通过英国Oxford Metrics Limited公司生产的VICON运动光学捕捉系统记录,包括12台高精度摄像机,采样频率为50 Hz;足底力信号利用AMTI测力板获取,采样率为1 000 Hz;表面肌电信号由16通道多导生理记录仪记录,采样频率为1 024 Hz。

完成数据获取后,对不同信号进行滤波和采样率同步化处理。另外,文献[27]进行了肌电爆发时刻与关节力矩产生时刻之间的时间差检测,结果表明,关节力矩产生滞后表面肌电信号50～80 ms;文献[11]在利用表面肌电信号进行关节力矩预测时将滞后时间定为40 ms。为此,本文综合各方面因素,将运动学和动力学数据都提前50 ms。利用同步化数据,按照第2、3节的方法分别对4名对象进行正向生物力学模型参数的标定和预测。

图5 试验设备与场景图

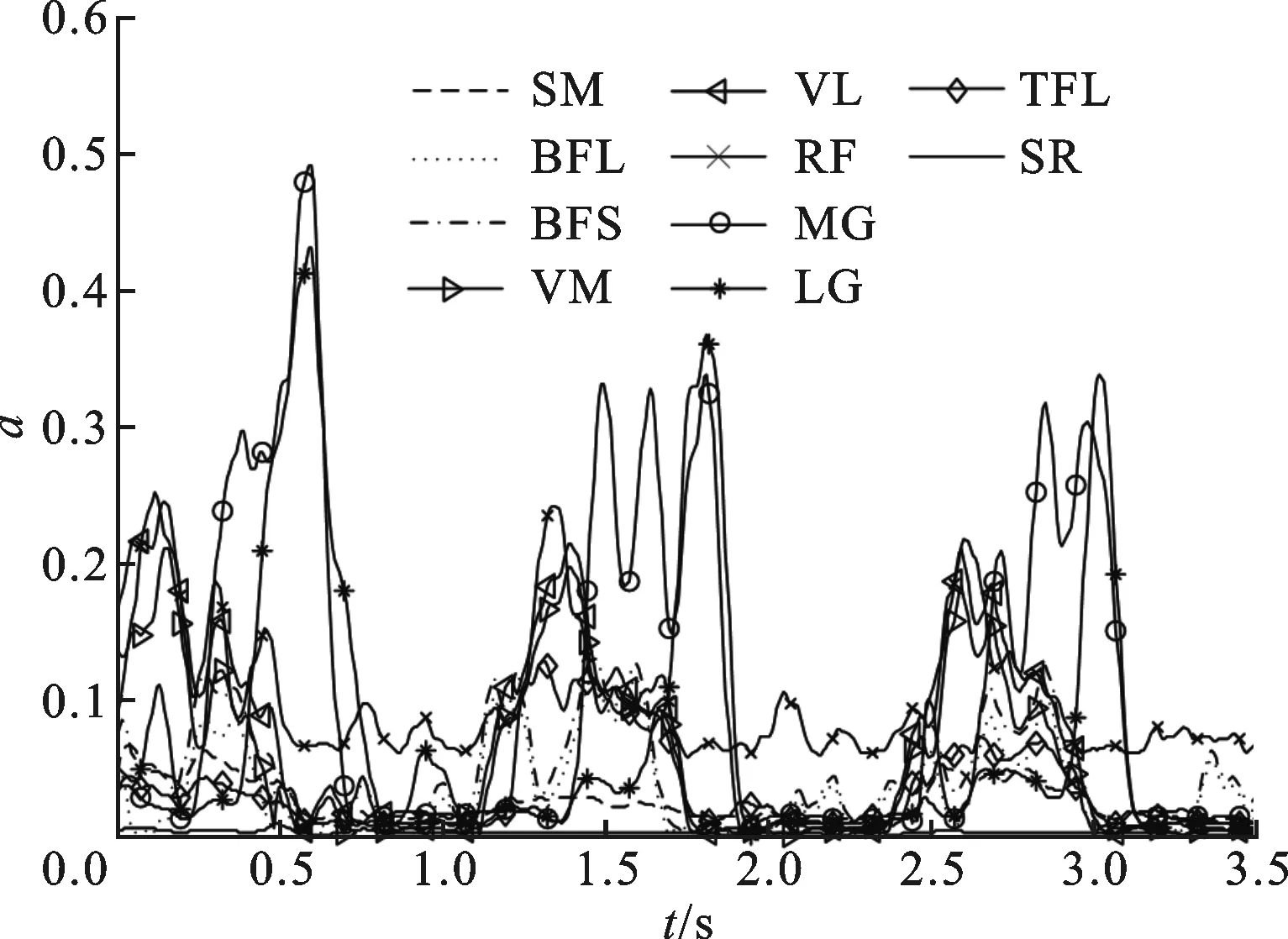
图6 对象A在3个步态周期中肌肉激活程度变化曲线

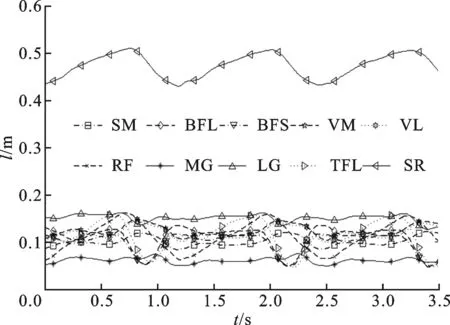
图7 对象A在3个步态周期中肌肉纤维长度变化曲线

以对象A为例,从3种步速下各选取一个步态周期数据作为优化样本,对模型进行标定。首先计算3个步态周期中的肌肉激活程度、肌肉运动参数以及关节力矩。图6是对象A在3个步态周期下10块肌肉的激活程度变化情况。从图中可以看出,在步态过程中,每块肌肉的激活程度变化非常复杂,但是在行走这一特定任务中,肌肉激活程度的变化趋势基本固定,主要在大小上存在差异。图7是对象A在3个步态周期下的肌肉纤维长度变化情况,可以看出,步态周期中肌纤维长度变化缓和,周期性很好,其中缝匠肌(SR)起始于骨盆髂前上棘,止于胫骨上端前缘,是人体最长的肌肉。其次,根据肌肉激活程度、肌肉运动学参数以及膝关节屈伸力矩值,对模型参数进行优化,初始种群规模为60,最大代数为400,优化结果误差如图8所示,优化最大误差达到6.25 N·m。此外,表1给出了对象A经过模型标定后的肌肉部分参数,包括肌肉最大力Famax、最优长度lopti和高斯函数中的标准差σ,同时还给出了文献[26]基于Hill肌肉力学模型给出的肌肉参数。在Delp模型中,通过测量21名尸体相关肌肉的横截面积取均值并乘以单位面积最大张力(61 N/cm2),得到肌肉最大力,因此肌肉之间最大力之比等于肌肉横截面积之比,而肌肉最优长度通过尸体肌肉直接测量得到。通过比较,本文优化得到的不同肌肉之间最大力之比与Delp模型中不同肌肉之间最大力之比关系一致,即遵循实际人体不同肌肉之间的发达程度关系,而肌肉的最优长度相差在1～2 cm之间,最长的肌肉缝匠肌(SR)相差为8 cm,这可以解释为是由于个体之间肌肉发达程度、身高差异引起的。

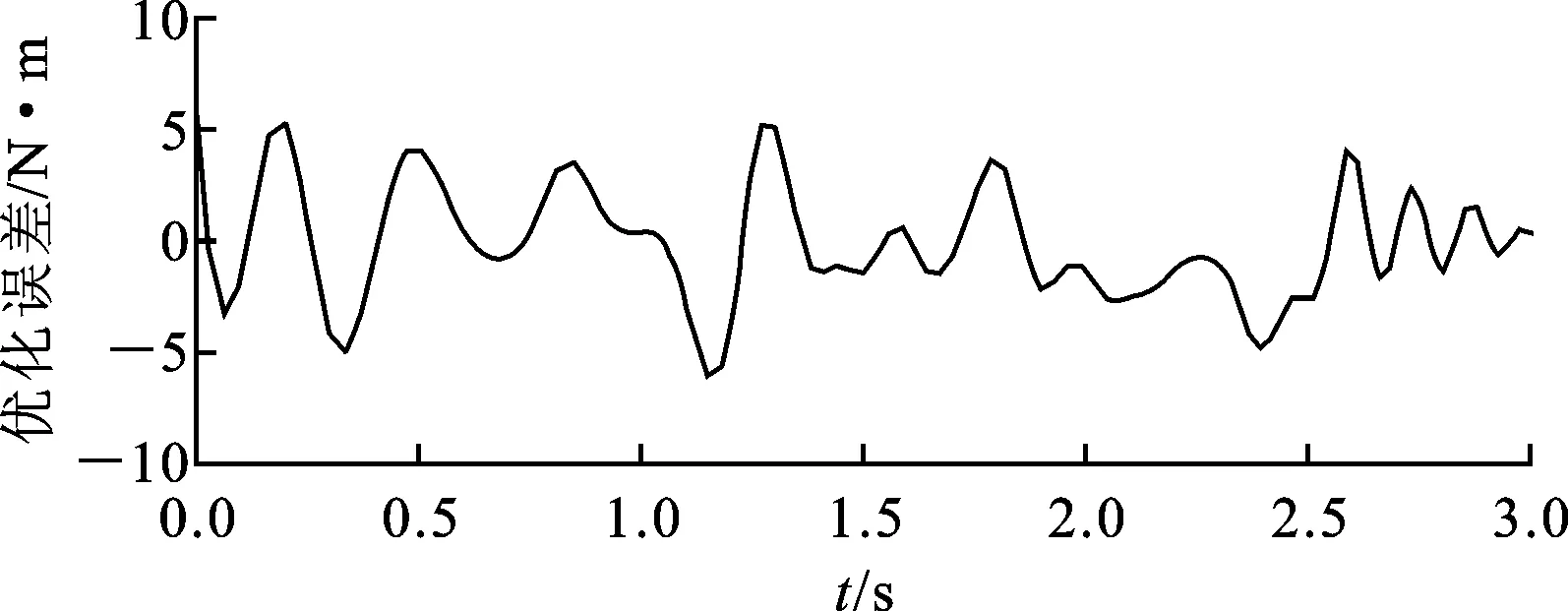
图8 模型参数优化结果误差

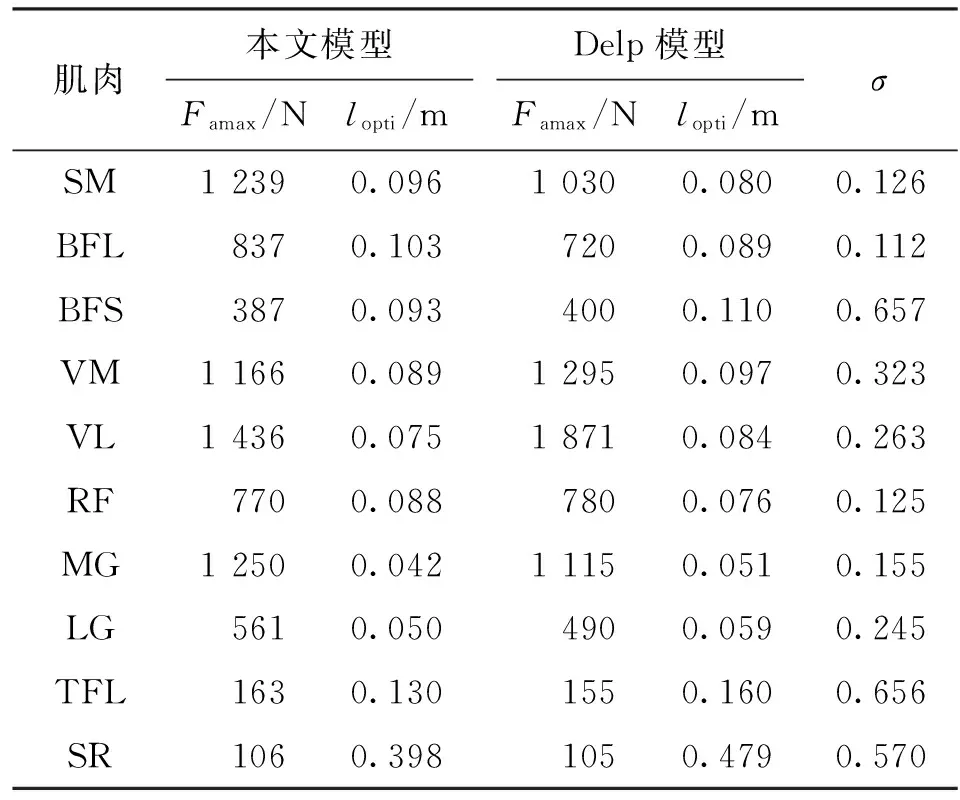
肌肉本文模型Famax/Nlopti/mDelp模型Famax/Nlopti/mσSM12390.09610300.0800.126BFL8370.1037200.0890.112BFS3870.0934000.1100.657VM11660.08912950.0970.323VL14360.07518710.0840.263RF7700.0887800.0760.125MG12500.04211150.0510.155LG5610.0504900.0590.245TFL1630.1301550.1600.656SR1060.3981050.4790.570

模型标定后,对所有对象步行过程中的膝关节屈伸方向动态力矩进行预测,图9给出了对象A某次步态下的预测结果,图中还给出了逆动力学计算的动态力矩曲线。从图中可以看出,建立的生物力学模型对步态行走过程中的膝关节动态力矩有较好的预测能力,能够快速地捕捉实际关节力矩的变化趋势,而且预测曲线波动较小。

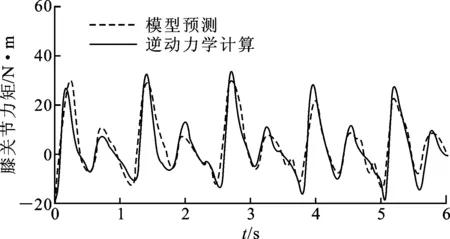
图9 膝关节动态关节力矩预测结果

另外,为定量描述模型的预测效果,采用最大绝对误差、平均残差以及预测值和实际值的线性相关程度R这3个参数来描述预测精度。对4名对象、3种不同步速下膝关节力矩预测结果进行定量统计,每名对象的描述参数都是对自身预测结果统计的平均值,如表2所示。从表中可以看出,正向生物力学模型预测最大绝对误差平均值为(11.0±1.32) N·m,平均残差为(4.43±0.698) N·m,平均线性相关系数为0.927±0.042。

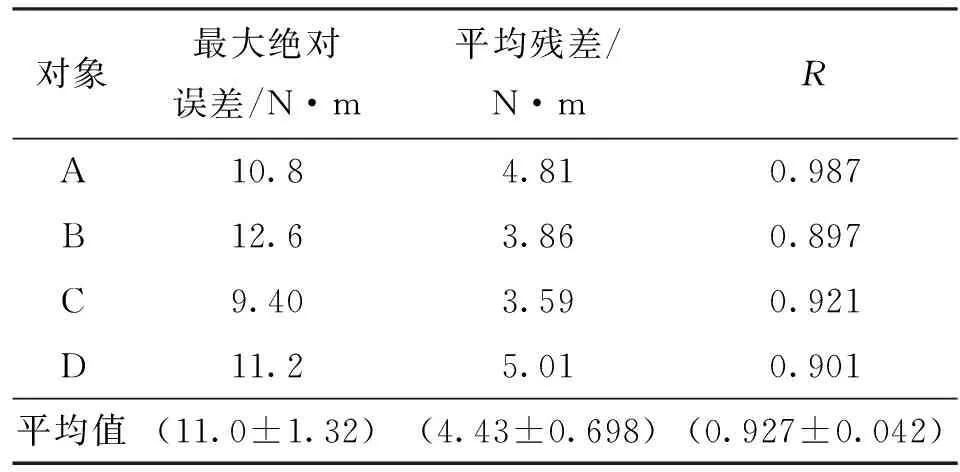
表2 所有对象预测结果统计

4 结 论

康复训练机器人能否有效地感知患者自身运动能力是其提供合理辅助的重要前提。基于生物电的人机交互接口技术是康复机器人领域的重要发展方向。本文在对人体下肢运动系统,包括神经、肌肉、骨骼、关节,各个组织的解剖结构和运动机理进行深入研究的基础上,建立了完整过程的正向生物力学模型,实现了基于表面肌电信号的下肢关节力矩动态预测。本文模型根据表面肌电信号的产生机理,从频率和幅值角度描述了肌肉激活程度与肌纤维激活及募集程度的关系,不同于过去只通过幅值信息描述肌肉激活程度,本文建立的肌肉生物电激活模型更全面。综合幅值和频率与单一的幅值相比,可以更加直接影响肌肉激活程度,进一步影响肌肉力大小及优化后参数的准确性,然而由于人体内肌力大小和肌肉参数目前无法直接测量,因此本文对于参数的影响尚不能给出具体评价,有待进一步研究。与Hill肌肉模型不同,本文根据肌丝滑移理论,建立能够描述生理结构和微观收缩机理的肌肉力学模型,因此更加完整和切合实际收缩过程。膝关节屈伸动态力矩的试验预测结果证明了本文模型的准确性和可靠性,为康复机器人运动感知能力的提高和人、机力柔顺交互研究提供了接口。同时,该生物力学模型的研究对不同运动的生理机理、探索运动康复规律、提高运动员成绩和防止运动损伤等领域存在应用价值。

[2] LUM P, REINKENSMEYER D, MAHONEY R, et al. Robotic devices for movement therapy after stroke: current status and challenges to clinical acceptance [J]. Topics in Stroke Rehabilitation, 2002, 8(4): 40-53.

[3] EKKELENKAMP R, VENEMAN J, VANDER KOOIJ H. LOPES: selective control of gait functions during the gait rehabilitation of CVA patients [C]∥9th International Conference on Rehabilitation Robotics. Piscataway, NJ, USA: IEEE, 2005: 361-364.

[4] 文忠, 钱晋武, 沈林勇, 等. 基于阻抗控制的步行康复训练机器人的轨迹自适应 [J]. 机器人, 2011, 33(1): 142-149. WEN Zhong, QIAN Jinwu, SHEN Linyong, et al. Trajectory adaptation for impedance control based walking rehabilitation training robot [J]. Robot, 2011, 33(1): 142-149.

[5] HAYASHI T, KAWAMOTO H, SANKAI Y. Control method of robot suit HAL working as operator’s muscle using biological and dynamical information [C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2005: 3063-3068.

[6] FLEISCHER C, HOMMEL G. A human-exoskeleton interface utilizing electromyography [J]. IEEE Transactions on Robotics, 2008, 24(4): 872-882.

[7] KREBS H I, PALAZZOLO J J, DIPIETRO L, et al. Rehabilitation robotics: performance based progressive robot-assisted therapy [J]. Autonomous Robots, 2003, 15(1): 7-20.

[8] PERRY J C, ROSEN J, BURNS S. Upper-limb powered exoskeleton design [J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(4): 408-417.

[9] KREBS H, VOLPE B, WILLIAMS D, et al. Robot-aided neurorehabilitation: a robot for wrist rehabilitation [J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007, 15(3): 327-335.

[10]MORITA S, KONDO T, ITO K. Estimation of forearm movement from EMG signal and application to prosthetic hand control [C]∥International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2001: 3692-3697.

[11]LLOYD D G, BESIER T F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo [J]. Journal of Biomechanics, 2003, 36(6): 765-776.

[12]BUCHANAN T S, LLOYD D G, MANAL K, et al. Neuromusculoskeletal modeling: estimation of muscle forces and joint moments and movements from measurements of neural command [J]. Journal of Applied Biomechanics, 2004, 20(4): 367-395.

[13]HILL A V. The heat of shortening and the dynamic constants of muscle [J]. Proceedings of the Royal Society of London: Series B Biological Sciences, 1938, 126(843): 136-195.

[14]GUO Zhao, FAN Yuanjie, ZHANG Jianjun, et al. A new 4M model-based human-machine interface for lower extremity exoskeleton robot [C]∥The 5th International Conference on Intelligent Robotics and Applications. Montreal, Canada: ICIRA, 2012: 545-554.

[15]YIN Y H, CHEN X. Bioelectrochemical control mechanism with variable-frequency regulation for skeletal muscle contraction-biomechanics of skeletal muscle based on the working mechanism of myosin motors (II) [J]. Science China: Technological Sciences, 2012, 55: 2115-2125.

[16]WANG W, DE STEFANO A, ALLEN R. A simulation model of the surface EMG signal for analysis of muscle activity during the gait cycle [J]. Computers in Biology and Medicine, 2006, 36(6): 601-618.

[17]HUXLEY A F, SIMMONS R M. Proposed mechanism of force generation in striated muscle [J]. Nature, 1971, 233(5321): 533-538.

[18]JULICHER F, AJDARI A, PROST J. Modeling molecular motors [J]. Reviews of Modern Physics, 1997, 69(4): 1269-1281.

[19]LECARPENTIER Y, BLANC F X, QUILLARD J, et al. Statistical mechanics of myosin molecular motors in skeletal muscles [J]. Journal of Theoretical Biology, 2005, 235(3): 381-392.

[20]YIN Yuehong, GUO Zhao. Collective mechanism of molecular motors and a dynamic mechanical model for sarcomere [J]. Science China: Technological Sciences, 2011, 54(8): 2130-2137.

[21]GOLLAPUDI S K, LIN D C. Experimental determination of sarcomere force-length relationship in type-I human skeletal muscle fibers [J]. Journal of Biomechanics, 2009, 42(13): 2011-2016.

[22]单大卯. 人体下肢肌肉功能模型及其应用的研究 [D]. 上海: 上海体育学院, 2003.

[23]CAMOMILLA V, CEREATTI A, VANNOZZI G, et al. An optimized protocol for hip joint center determination using the functional method [J]. Journal of Biomechanics, 2006, 39(6): 1096-1106.

[24]HARRINGTON M E, ZAVATSKY A B, LAWSON S E, et al. Prediction of the hip joint centre in adults, children, and patients with cerebral palsy based on magnetic resonance imaging [J]. Journal of Biomechanics, 2007, 40(3): 595-602.

[25]VAUGHAN C L, DAVIS B L, O’CONNOR J C. Dynamics of human gait [M]. Champaign, Illinois, USA: Human Kinetics Publishers, 1992: 83-106.

[26]ARNOLD E M, WARD S R, LIEBER R L, et al. A model of the lower limb for analysis of human movement [J]. Annals of Biomedical Engineering, 2010, 38(2): 269-279.

[27]HOWATSON G, GLAISTER M, BROUNER J, et al. The reliability of electromechanical delay and torque during isometric and concentric isokinetic contractions [J]. Journal of Electromyography and Kinesiology, 2009, 19(5): 975-979.

(编辑 杜秀杰)

Prediction Model for Dynamic Joint Torque of Lower Limb with Surface EMG

CHEN Jiangcheng,ZHANG Xiaodong,LI Rui,SHI Qiangyong,WANG He

(Key Laboratory of Education Ministry for Modern Design & Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China)

To achieve the dynamic joint torque decoding from surface electromyography (EMG), the forward biomechanical model of lower limb motor system, which relates the surface EMG and joint torque, is established. The dynamic surface EMG to skeletal muscle activation model is constructed from the perspective of amplitude and frequency. Then the muscle contraction model reflecting physiological structure and micromechanical properties is constructed according to the sliding-filament theory. The force direction and displacement vector of active muscle are determined and the transformation from muscle force to joint moment is realized. The dynamic calibration for the forward biomechanical model using the exact joint torque value obtained with Newton-Eular method is finally put forward. Following the calibration, the flexion/extension (FE) knee joint torque of four objects under different speed walking is predicted. The results show that the forward biomechanical model can capture the general shape and timing of the joint torque, the maximum absolute error is (11.0±1.32) N·m, the mean residual error is (4.43±0.698) N·m, and the linear relationship between predicted and exact knee FE torque reaches 0.927±0.042. This prediction model provides an interface for the study of force interaction pattern in the process of human-machine cooperation in training.

surface EMG; joint torque prediction; muscle model; forward biomechanics

2015-03-08。

陈江城(1987—),男,博士生;张小栋(通信作者),男,教授,博士生导师。

国家高技术研究发展计划资助项目(2015AA042301);国家自然科学基金重大研究计划资助项目(91420301)。

时间:2015-09-13

10.7652/xjtuxb201512005

TP242

A

0253-987X(2015)12-0026-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150913.1822.002.html