利用高斯混合概率假设密度滤波器对扩展目标量测集进行划分

孔云波,冯新喜,危璋

(空军工程大学信息与导航学院, 710077, 西安)



利用高斯混合概率假设密度滤波器对扩展目标量测集进行划分

孔云波,冯新喜,危璋

(空军工程大学信息与导航学院, 710077, 西安)

针对杂波环境下多扩展目标高斯混合概率假设密度(ET-GMPHD)量测集划分难、计算量大的问题,提出了一种新的基于网格密度分布和谱聚类的扩展目标量测集划分方法。利用动态网格生成技术来获得量测集的网格密度分布;在获得网格划分后,将全部量测数据映射到网格单元中并统计网格单元的密度,且采用双密度阀值法来滤除量测集中的杂波;在谱聚类算法中利用密度敏感距离测度对去除杂波后的量测集构造相似矩阵,继而变换得到拉普拉斯矩阵;利用k-均值聚类算法对拉普拉斯矩阵的特征向量进行聚类划分。采用网格密度划分法滤除量测集中的杂波,使划分子集尽可能多地包含真实量测,增加划分子集与量测集合的近似度,从而在减少计算量的同时保证算法的跟踪性能损失不大。仿真实验表明,与典型的量测集划分算法相比,所提方法在跟踪误差损失约5%的前提下,计算效率提高了38%以上,具有更好的性能。

扩展目标;网格密度;谱聚类;量测集划分

在传统的目标跟踪方法中,由于目标与传感器之间的距离远远大于目标的大小,因此通常假设每个目标在一个采样周期内最多产生一个量测。然而,随着传感器分辨率的不断提高以及目标与传感器距离的不断缩小,目标占据的雷达分辨单元逐渐增加,从而使得一个目标在一个采样周期内可产生多个量测,这类目标称为扩展目标。自动雷达对车辆的跟踪、激光测距雷达对人运动情况的跟踪以及地面或海事雷达站对近距飞机或舰船的跟踪问题都属于扩展目标跟踪的研究范畴[1]。

近年来,基于随机有限集的多目标跟踪由于无需数据关联且能在处理跟踪问题的过程中同步获得目标数的动态估计,因此受到越来越多的关注。2009年,Mahler提出将概率假设密度滤波器用于扩展目标的跟踪,推导获得了扩展目标-概率假设密度(ET-PHD)滤波器[2]。2010年,Granstrom等在线性高斯假设条件下给出了ET-PHD滤波器的高斯混合实现方法,并通过仿真验证了该滤波器的有效性[3]。在此基础上,Orguner等人针对扩展目标提出了扩展目标势概率假设密度(CPHD)滤波,并用高斯混合得以实现[4]。连峰等针对扩展目标和群目标提出了一种标准CPHD滤波[5]。然而,由Mahler的推导可知,无论是扩展目标高斯混合-概率密度(ET-GM-PHD)和ET-GM-CPHD滤波,其精确滤波更新都需要当前量测集的所有可能划分,而量测集的所有可能划分数目随量测数的增加而急剧增加,是一个贝尔数,除简单情况外,一般是计算不可行的。因此,寻找快速的量测集划分方法是实现扩展目标高斯混合概率假设密度滤波的关键。针对此问题,文献[3]提出了一种基于距离原则的假设检验量测集划分方法,为保证跟踪性能,该算法需要选取阀值区间中所有的值来形成足够多的划分,而划分数将随着目标数的增加而急剧增加,进而增加了算法的计算量。文献[6]提出了一种基于快速模糊自适应谐振理论(ART)的量测集划分方法,该算法能够对量测集进行快速和稳定地划分,然而在密集目标和杂波情况下,模糊ART固有的缺陷使得该算法容易出现“饱和”问题,从而出现分类错误。

本文针对杂波环境下多扩展目标高斯混合PHD量测集划分难、计算量大的问题,提出了一种新的基于网格密度分布和谱聚类的扩展目标量测集划分方法。该方法首先利用动态网格划分来估计量测集的密度分布,并采用双密度阀值法来滤除量测集中的杂波,然后在谱聚类算法中利用密度敏感距离测度对去除杂波后的量测集构造相似矩阵,继而变换得到拉普拉斯矩阵,最后利用k-均值聚类算法对拉普拉斯矩阵的特征向量进行聚类划分。

1 扩展目标高斯混合PHD滤波器

PHD滤波作为一种近似的算法,可以用来降低多目标贝叶斯滤波器的计算复杂度。高斯混合概率假设密度滤波是PHD滤波的一种实现形式,通过带权值的高斯分量来近似目标强度函数,它假设场景中的每一个目标都服从线性混合高斯模型。由于扩展目标高斯混合PHD滤波器的预测更新方程和标准的高斯混合PHD滤波的预测更新方程一致[7-8],因此本文仅给出扩展目标量测更新方程的具体形式和推导过程。

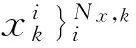
(1)

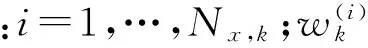
假设预测PHD高斯混合表示为

(2)

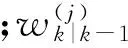
假设量测个数服从泊松分布,则量测更新PHD可表示为

(3)

(4)

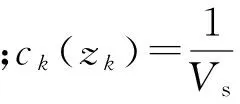
为阐述量测集划分在扩展目标高斯混合PHD滤波中的重要性,给出一个例子,若某一时刻量测集Z={z1,z2,z3},则其所有划分为:p1={{z1,z2,z3}},p2={{z1},{z2},{z3}},p3={{z1,z2},{z3}},p4={{z1,z3},{z2}},p5={{z1},{z2,z3}}。随着量测集中元素数目的增加,所有可能划分的数量将急剧增加,特别是杂波密集的情况下,计算一般是不可行的。因此,本文提出了一种新的基于网格密度分布和谱聚类的扩展目标量测集划分方法。

2 基于网格密度分布和谱聚类的量测划分方法

2.1 基于网格密度分布的杂波剔除方法

基于网格密度分布的杂波剔除方法结合密度估计和网格划分思想的优点,用数据空间网格化的方法来节省运算时间,根据网格间的密度关系来剔除杂波,提取量测信息。其主要思想是:首先对量测数据空间进行动态网格划分,然后将量测信息汇总到其所在的单元格中并统计其密度,最后采用双密度阀值和动态网格边界优化来剔除量测集中的杂波点。

2.1.1 动态网格划分 在网格密度杂波剔除算法中的第一步且关键的一步是网格的划分方法,网格的划分是影响剔除算法的关键因素,划分粒度太细会导致算法计算量增加且容易将真实目标肢解,从而使得真实量测当作杂波被剔除,划分粒度太粗又会导致真实量测与杂波无法分离。本文采用动态网格密度划分法,在每一时刻自适应确定网格划分,减小人为因素的影响。

采用网格划分对数据处理的本质是数据压缩,而数据每一维的划分数就代表了数据压缩的程度。定义数据压缩率γ,则k时刻网格的划分数

(5)

式中:Nz,k表示k时刻量测z的个数;d表示数据维数。

2.1.2 双密度阀值 在确定网格划分后,网格密度阀值的确定对杂波的剔除结果有着很大的影响,如果选择得不合理很可能造成信息的多选和漏选。传统的方法采用单密度阀值判断高低密度网格,容易将真实量测和杂波相混淆[9]。因此,借鉴平均密度的思想,在原有密度阀值的基础上增加一个核心密度阀值,从而利用双密度阀值来剔除杂波信息。

假设划分网格单元个数为C,den(Ci)表示网格密度,max(den(Ci))为生成相交网格最高密度网格,min(den(Ci))为生成相交网格最低密度网格。密度阀值ε1和核心密度阀值ε2的定义分别为

(6)

(7)

定义网格单元密度大于核心密度阀值的网格单元称为核心网格,网格单元密度大于密度阀值的网格单元称为高密度网格,网格单元密度小于密度阀值的网格单元称为低密度网格,核心网格也属于高密度网格。

在获得网格划分后,将全部量测数据映射到网格单元中并统计网格单元的密度。在此基础上,利用式(5)、式(6)计算密度阀值和核心密度阀值。若直接采用双密度阀值法来排除杂波点,则有可能丢失边界信息。为正确提取边界点,本文采用边界优化技术,对低密度网格区域和不包含核心网格单元的高密度网格区域的量测点进行扫描,并以该量测点为中心,依据式(5)划分的网格为边长建立动态网格,统计落入其内量测的密度。若该网格密度值大于ε2,则将其保留;反之,将其视为杂波点舍去。

2.1.3 剔除算法具体步骤 基于双密度阀值的网格密度杂波剔除算法的主要操作步骤如下。

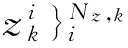
步骤2 利用式(5)求解量测数据每一维的网格划分数,并进行网格单元的划分。

步骤3 将全部量测数据映射到网格单元中并统计网格单元的密度。

步骤4 网格单元的密度定义为网格中含有量测的个数,在此基础上,利用式(6)、式(7)计算密度阀值和核心密度阀值。

步骤5 在完成上述步骤后,依据步骤4计算的密度阀值来进行量测剔除。由分析可知,只有含有核心网格单元的高密度网格区域才是包含真实的量测值,低密度网格区域和不包含核心网格单元的高密度网格区域都是杂波网格。依据此原则对所有的单元格进行处理。

步骤6 利用网格边界优化技术,对经过步骤5处理的量测点集进行边界点提取。

2.2 基于谱聚类的量测划分

2.2.1 谱聚类算法 谱聚类算法[10]的思想来源于谱图划分理论,如果将数据集看成一个无向完全图,数据点作为图的顶点,数据点间的相似度量化为定点连接边的权值,则聚类问题就转化为图的划分问题。基于图论的最优划分准则就是使划分成的2个子图内部相似度最大,子图之间的相似度最小。划分准则的好坏直接影响到聚类结果的优劣。常见的划分准则有最小划分、平均划分、正则划分、最小最大化划分、比率划分等。谱聚类算法对聚类的数据空间结构不做强的假设,相比传统的k-均值算法等需要建立在凸球形的样本空间的缺点,谱聚具有能在任意形状的样本空间上聚类且收敛于全局最优解的优点。

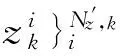
(8)

2.2.2 基于谱聚类的量测划分 基于谱聚类的量测划分思想是首先利用构建的密度敏感距离测度对去除杂波后的量测集构造相似矩阵S,然后通过变化得到拉普拉斯矩阵F,再求解拉普拉斯矩阵的特征值和特征向量,最后选择合适的特征向量进行聚类。相似度矩阵S中元素反映了量测数据之间的相似性度量,优质的相似性度量应该能同时反映出量测数据的局部一致性和全局一致性。局部一致性是指在空间位置上相邻的数据点具有较高的相似性,全局一致性是指属于同一类的数据点具有较好的相似性。本文采用一种既满足局部一致性又满足全局一致性的相似性度量-密度敏感相似性度量[11],该度量可以缩短同一类数据点之间的距离,同时放大不同类数据点之间的距离,从而有效描述数据点的实际分布情况,达到好的聚类效果。

下面给出基于密度敏感的谱聚类量测划分方法的计算步骤。

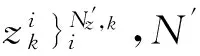
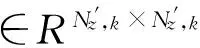
(9)

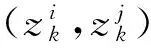
(10)

(11)

式中:L(pt,pt+1)表示两点间密度可调节的线段长度;dist(pt,pt+1)表示两数据点之间的欧氏距离;ρ>1为密度参数。

步骤3 构造对角矩阵D。

步骤4 按照式(8)构造拉普拉斯矩阵F。

步骤5 求矩阵F的K个最大特征值对应的特征向量v1,v2,…,vK,构造矩阵

(12)

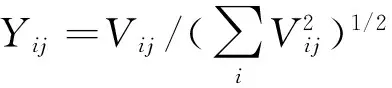
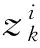
步骤8 重复步骤5～7,继而得到量测集的划分子集。

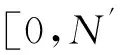
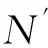
(13)

(14)

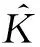
(15)

2.3 计算时间复杂度分析

为了分析基于网格密度和谱聚类的扩展目标量测集划分方法,设Nz,k为k时刻的量测数。该算法的计算复杂度由两部分组成:第一部分是利用网格密度剔除杂波;第二部分为利用谱聚类对去除杂波后的量测集划分。

第一部分各步骤的计算量为:对量测集进行归一化的计算复杂度为O(Nz,k);网格单元的划分的计算复杂度为O(d(Nz,k+N1)+N2),其中N1表示密集区域量测点的个数,N2表示空间划分的网格数;将量测点映射到划分的单元格中的计算复杂度为O(Nz,k);统计每个网格单元的密度计算复杂度为O(Nz,k+N2);对杂波量测进行删除的计算复杂度为O(N2)。

3 仿真实验与分析

考虑二维平面内单传感器跟踪4个目标的运动情况,设二维观测x区域为[-1 000,1 000],y区域为[-1 000,1 000],传感器坐标S=(1 000,0),采样周期T=1 s,4个目标相继出现,各目标初始状态以及出生和消亡的时间如表1所示。整个观测时间持续100 s。

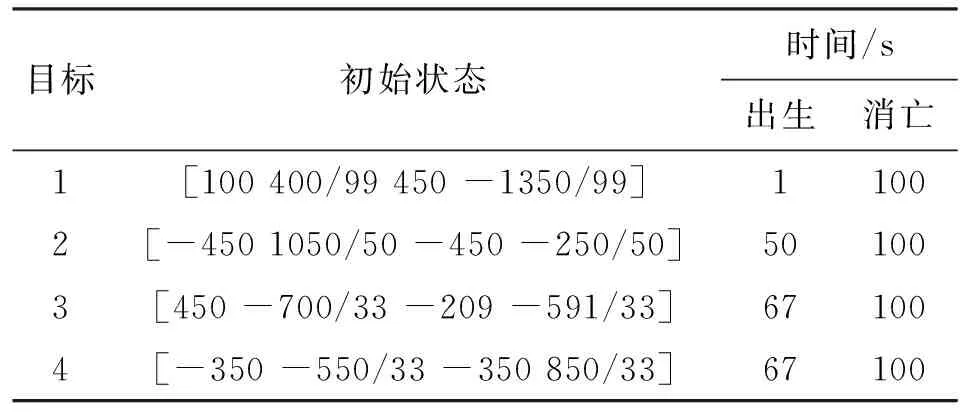
表1 目标初始状态和运动轨迹

扩展目标运动模型为

(16)

式中:xk=[xk,vx,yk,vy]T,xk、yk表示目标的位置坐标,vx、vy分别表示对应的速度分量;过程噪声[w1,k,w2,k]T是零均值高斯白噪声,其分量标准差σw1=σw2=2 m/s2。简单起见,不考虑目标衍生过程,新生目标的PHD为

(17)

式中:mb=[250,0,250,0]T;Pb=diag(100,25,100,25)

扩展目标量测方程为

(18)

式中:量测噪声[R1,k,R2,k]T是零均值高斯白噪声,其分量标准差σR1=σR2=20 m。目标存活概率为0.99,检测概率为0.99。每一时刻每个目标产生的量测个数服从均值为10的泊松分布,每一时刻产生的杂波数也服从均值为10的泊松分布,且在观测区域内均匀分布。仿真参数设置最大高斯分量数目Jmax=100,修剪门限为10-4,合并门限为4。根据实验经验,综合考虑精度和计算量,设置参数为:数据压缩率γ=0.5,密度敏感参数ρ=2,k-均值迭代次数u=5。

为验证本文所提量测划分方法的有效性,首先讨论压缩率γ对量测划分方法的影响。图1给出了一次蒙特卡罗仿真中k=58、压缩率γ为0.7时的杂波剔除情况。从图中可以看出,虽然经过双密度阀值操作后,部分来源于目标的边界量测点被舍弃,但经过动态网格边界优化操作后,部分符合阀值的边界量测点又重新被保留。表2给出了100次蒙特卡罗仿真情况下,杂波剔除前后杂波占比的平均值与压缩率的关系,从表中可以看出,随着压缩率的减小,杂波占比在逐渐减小,但同时算法的计算量也在增加,因此经多次实验并综合算法精度和复杂度,本文在后面的实验中选取γ=0.5。

压缩率杂波占比的平均值/%剔除杂波前剔除杂波后0.737.446.840.537.444.790.837.443.34

为比较采用距离划分和本文所提算法用于扩展目标高斯混合概率假设密度滤波器的计算复杂度和有效性,进行了100次蒙特卡罗仿真实验。首先考虑每一时刻杂波数服从均值为10的泊松分布的情况。杂波环境下的态势图如图2所示。

图3给出了仅两种量测集划分算法平均运算时间对比图,从图中可以看出,采用本文所提的算法进行量测集划分明显减小了计算量,这是由于算法首先采用了网格杂波密度法将大量的杂波剔除,在此基础上对划分数目进行约束,大大减少了量测集的划分数,从而使得本文所提算法减小了计算量,这与计算复杂度的分析结果相符。表3给出了量测划分平均时间随杂波占比的平均值的变化情况,从表中可以看出,随着杂波占比的平均值的增大,两种算法的运行时间都有所增加,但本文所提算法的平均运行时间增加率明显小于基于距离划分的平均运算时间,且运算效率提高了约38%,从而进一步说明了本文所提算法确实提高了运算效率。

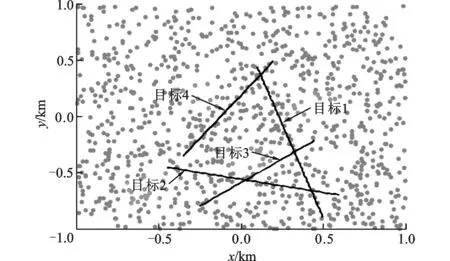
图2 杂波态势图

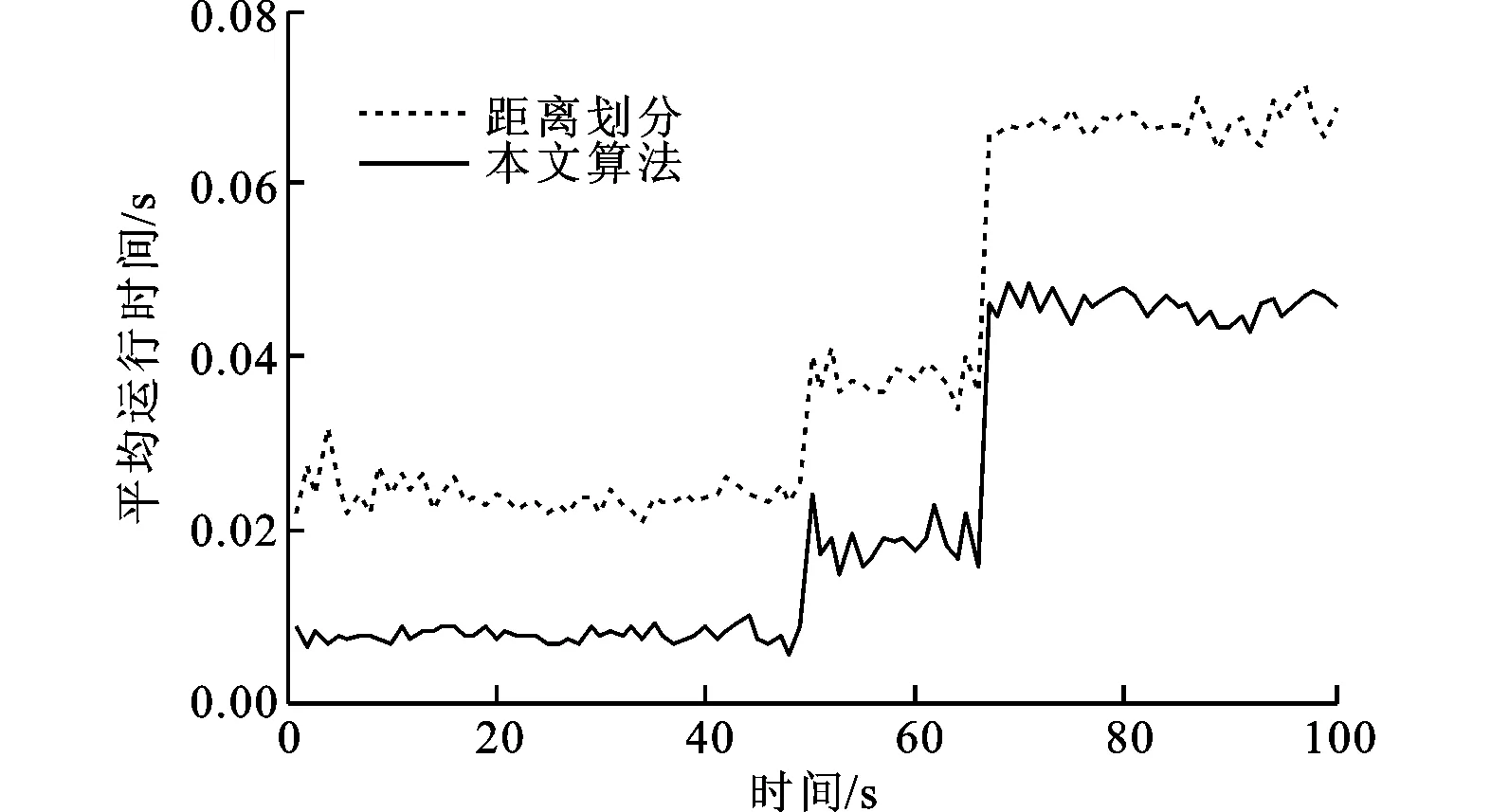
图3 两种量测集划分算法平均运行时间比较

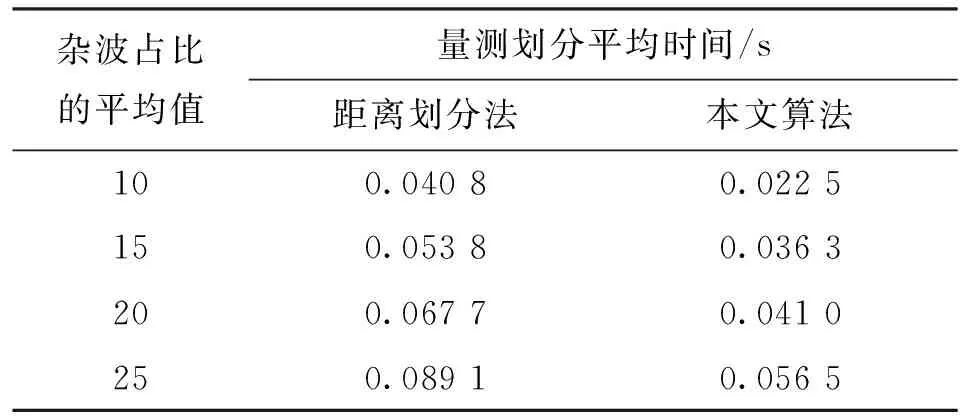
杂波占比的平均值量测划分平均时间/s距离划分法本文算法100.04080.0225150.05380.0363200.06770.0410250.08910.0565

图4给出了100次蒙特卡罗仿真实验平均后得到的两种算法对多目标数估计随时间变化的曲线。由图4看出,两种算法均能较好地收敛到真实的目标数,并且在目标数发生变化的时刻,两种算法对目标数目估计有较大的波动,但一旦进入目标数目恒定阶段,均能准确估计出目标数。

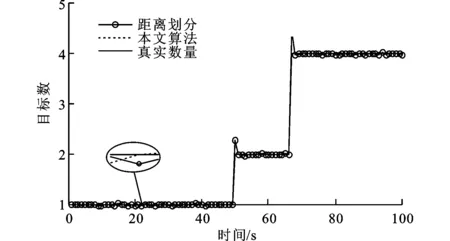
图4 两种算法平均势估计图

由于扩展目标高斯混合概率假设密度滤波器没有进行数据关联,均方误差(RMSE)无法对滤波器的性能进行评价。为统计两种算法的平均性能,本文采用平均脱靶距离OSPA对两种算法的性能进行评价,OSPA距离的计算式为

(19)

在OSPA距离中,参数c和p的选择对集合势误差和位置误差有重要的影响。在实验中参数c=200,参数p=2。图5为100次蒙特卡罗仿真实验结果,从图中可以看出,相比基于距离划分的扩展目标高斯混合概率假设密度滤波器的跟踪结果,在目标数发生变化的时刻,本文所提算法的滤波误差有所增加,但在大多数时刻,两种算法的跟踪误差相差不大,即算法以牺牲较小的跟踪性能来减少算法的运算时间。另外,在目标个数发生变化的时刻,两种算法所得到的OSPA曲线震荡较大、波峰较高,因此也可以看出曲线主要反映的是目标数的变化。

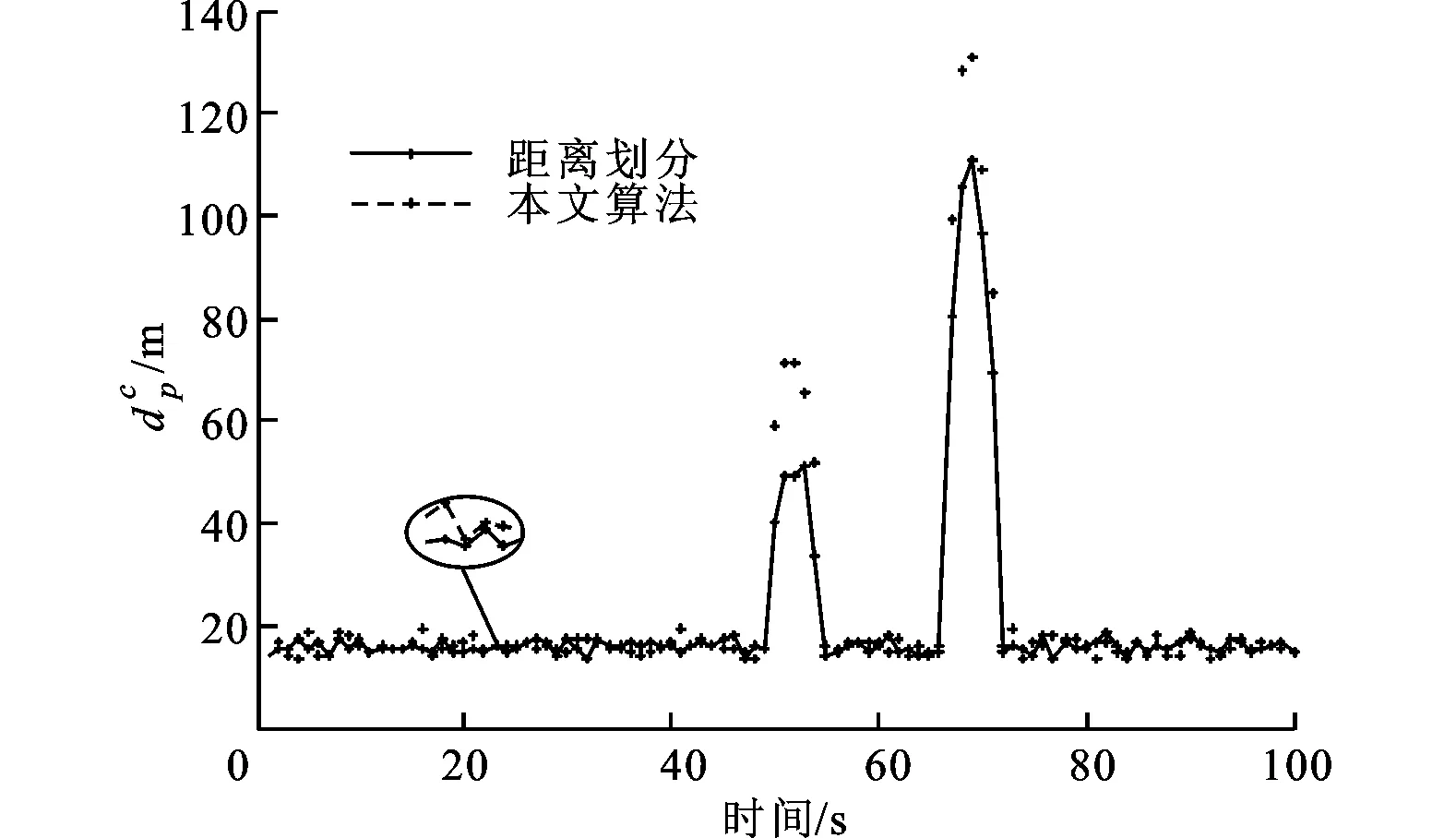
图5 平均OSPA图

图6给出了100次蒙特卡罗仿真实验情况下OSPA均值随杂波均值的变化情况,从图中可以看出,随着杂波均值的增大,两种算法的OSPA均值均增大,但本文所提算法的OSPA均值略高于基于距离划分的滤波器的OSPA均值,平均增大约5%。

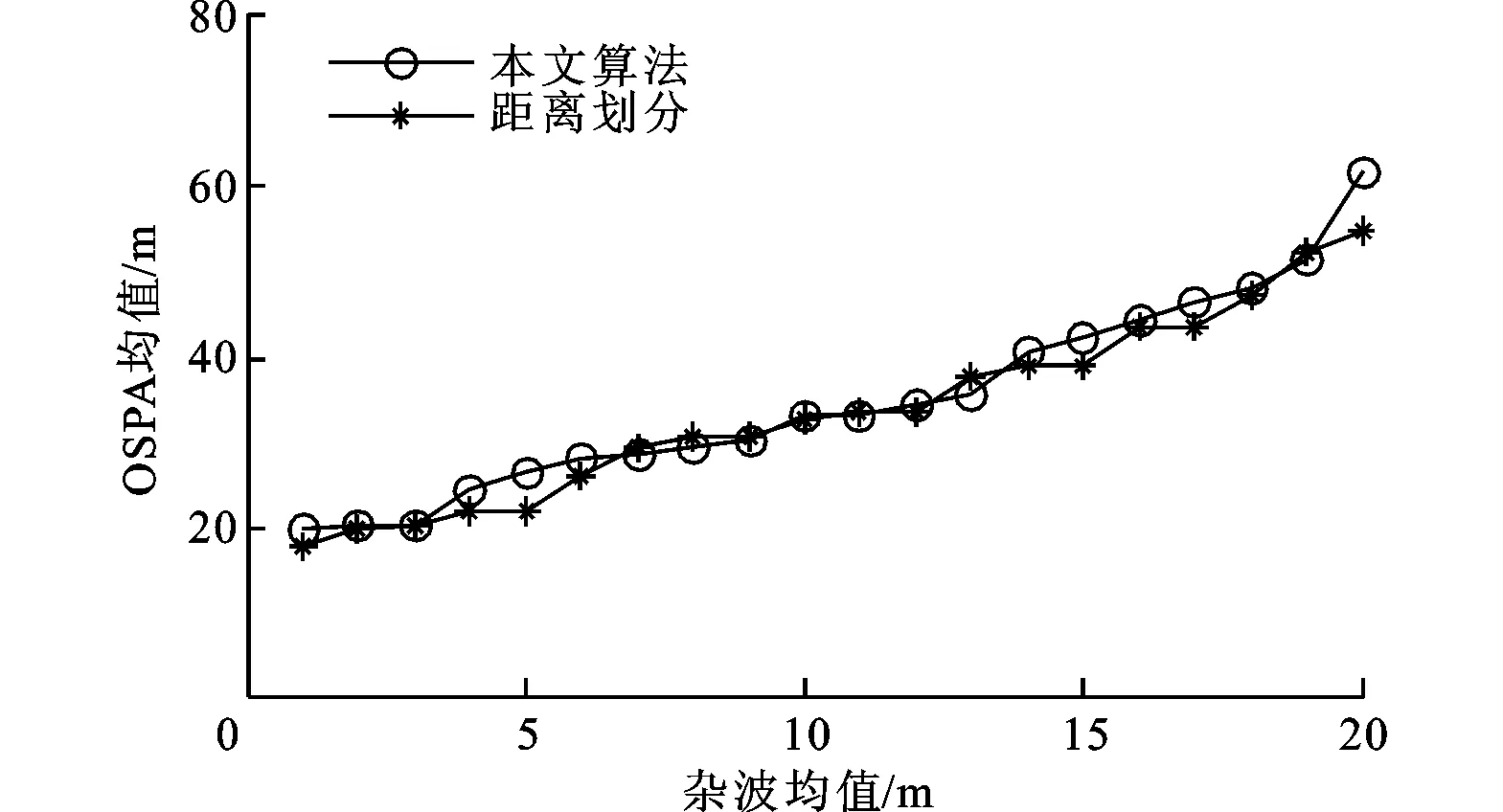
图6 OSPA均值与杂波均值的关系图

4 结 论

针对扩展目标高斯混合概率假设密度量测集划分的问题,本文提出了一种基于网格密度和谱聚类的扩展目标量测集划分方法。该方法采用网格密度划分法滤除量测集中的杂波,使划分子集尽可能多地包含真实量测,增加划分子集与量测集合的近似度,从而使得算法在减小计算量的同时,保证算法的跟踪性能损失不大。实验结果表明,与典型的量测集划分方法相比,本文所提算法具有更好的性能。

[1] GRANSTROM K, LUNDQUIST C, ORGUNER U. Extended target tracking using a Gaussian-mixture PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.

[2] MAHLER R. PHD filters for nonstandard targets: I extended targets [C]∥Proceedings of the 12th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2009: 915-921.

[3] GRANSTROM K, LUNDQUIST C, ORGUNER U. A Gaussian mixture PHD filter for extended target tracking [C]∥Proceedings of the 13th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2010: 1-8.

[4] ORGUNER U C, LUNDQUIST C, GRANSTROM K. Extended target tracking with a cardinalized probability hypothesis density filter [C]∥Proceedings of the 14th International Conference on Indormation Fusion. Piscataway, NJ, USA: IEEE, 2011: 5-8.

[5] LIAN F, HAN C Z. Unified cardinalized probability hypothesis density filters for extended targets and unresolved targets [J]. Signal Processing, 2012, 92(7): 1729-1744.

[6] ZHANG Y Q, JI H B. A novel fast partitioning algorithm for extended target tracking using a Gaussian mixture PHD filter [J]. Signal Processing, 2013, 93 (11): 2975-2985.

[7] 闫小喜, 韩崇昭, 李威, 等. 拓展目标量测集分割算法 [J]. 西安交通大学学报, 2014, 48(9): 19-23. YAN Xiaoxi, HAN Chongzhao, LI Wei, et al. A partition algorithm of measurement sets for extended objects [J]. Journal of Xi’an Jiaotong University, 2014, 48(9): 19-23.

[8] 瑚成祥, 刘贵喜, 董亮, 等. 区域杂波估计的多目标跟踪方法 [J]. 航空学报, 2014, 35(4): 1091-1101. HU Chengxiang, LIU Guixi, Dong Liang, et al. Region clutter estimation method for multi-target tracking [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 1091-1101.

[9] 王军, 张冰. 基于动态网格密度聚类的雷达信息分选算法 [J]. 现代电子技术, 2013, 11(1): 1-4. WANG Jun, ZHANG Bing. A radar signal sorting algorithm based on dynamic grid density clustering [J]. Modern Electronics Technique, 2013, 11(1): 1-4.

[10]黄发良, 黄名选, 元昌安, 等. 网络重叠社区发现的谱聚类集成算法 [J]. 控制与决策, 2014, 29(4): 713-718. HUANG Faliang, HUANG Mingxuan, YUAN Chang’an, et al. Spectral clustering ensemble algorithm for discovering overlapping communities in social networks [J]. Control and Decision, 2014, 29(4): 713-718.

[11]张亚平, 杨明. 一种基于密度敏感的自适应谱聚类算法 [J]. 数学的实践与认识, 2013, 43(20): 150-156. ZHANG Yaping, YANG Ming. A kind of density sensitive adaptive spectral clustering algorithm [J]. Mathematics in Practice and Theory, 2013, 43(20): 150-156.

[12]TSAI C W, YANG C S, CHIANG M C. A time efficient pattern reduction algorithm fork-means based clustering [C]∥IEEE International Conference on Systems, Man and Cybernetics. Piscataway, NJ, USA: IEEE, 2007: 504-509.

[13]LI Y X, XIAO H T, SONG Z Y. A new multiple extended target tracking algorithm using PHD filter [J]. Signal Processing, 2013, 93(7): 3578-3588.

[本刊相关文献链接]

陶庆,孙文磊,周建星.考虑齿圈柔性的行星传动系统固有特性与灵敏度研究.2015,49(3):113-120.[doi:10.7652/xjtuxb201503018]

和文强,秦国良.谱元方法求解对流扩散方程及其稳定性分析.2015,49(1):1-6.[doi:10.7652/xjtuxb201501001]

闫小喜,韩崇昭,李威,等.拓展目标量测集合分割算法.2014,48(9):19-23.[doi:10.7652/xjtuxb201409004]

张光华,连峰,韩崇昭,等.高斯混合扩展目标多伯努利滤波器.2014,48(10):9-14.[doi:10./xjtuxb201410002]

郑卜祥,姜歌东,王文君,等.超快脉冲激光对钛合金的烧蚀特性与作用机理.2014,48(12):21-28.[doi:10.7652/xjtuxb 201412004]

韩玉兰,朱洪艳,韩崇昭,等.多扩展目标的高斯混合概率假设密度滤波器.2014,48(4):95-101.[doi:10.7652/xjtuxb 201404017]

倪中非,黄斌科,师振盛.用于非规则波导传输特性分析的高效坐标变换法.2014,48(8):18-22.[doi:10.7652/xjtuxb 201408004]

问翔,刘宏伟,包敏.距离扩展目标回波序列的慢时间谱积累检测器.2013,47(10):18-24.[doi:10.7652/xjtuxb201310 004]

杨清宇,孙凤伟,张曌,等.利用测地线距离的改进谱聚类算法.2012,46(8):1-7.[doi:10.7652/xjtuxb201208001]

张慧,韩崇昭,闫小喜.概率假设密度滤波的谱聚类目标状态提取方法.2012,46(2):1-5.[doi:10.7652/xjtuxb201202001]

(编辑 赵炜)

A Measurement Set Partitioning for Extended Target Tracking Using a Gaussian Mixture Extended-Target Gaussian Mixture Probability Hypothesis Density Filter

KONG Yunbo,FENG Xinxi,WEI Zhang

(School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China)

A new measurement set partitioning based on grid density and spectral clustering is proposed to overcome the problem that it is impossible to implement all the possible partitioning of a measurement set by the filters with extended-target Gaussian mixture probability hypothesis density. Firstly, the dynamic grid generation technique is used to acquire the grid density of measurement set, then the double-density threshold is adopted to remove the clutters of measurements set. Lastly, the spectral clustering based on the sensitive distance is applied in partitioning the measurement set from which the clutters have been removed. Simulation results show that, compared with the typical partition algorithm of measurement set, though the tracking performance of the proposed algorithm loses 5%, the computational efficiency is increased by 38%.

extended target; grid density; spectral clustering; measurement set partitioning

2014-12-08。

孔云波(1987—),男,博士生;冯新喜(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61403414);国家重点实验室开放基金资助项目(2014K0304B)。

时间:2015-04-22

10.7652/xjtuxb201507021

TN953

A

0253-987X(2015)07-0126-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150422.1444.001.html