采用代数建模方法的自适应观测器设计

韩冬,刘俊

(清华大学自动化系, 100084, 北京)



采用代数建模方法的自适应观测器设计

韩冬,刘俊

(清华大学自动化系, 100084, 北京)

针对伴有未知输入的一类线性时不变系统,当观测器匹配条件不满足时,研究了自适应观测器的设计问题。通过将未知输入划分为匹配未知输入和不匹配未知输入两部分,并假设不匹配未知输入可以表述为一个动态系统,从而可得一个满足匹配条件的增广系统;对于该增广系统讨论了自适应观测器的存在条件,给出了自适应观测器的设计方法,这种自适应观测器不仅可以观测原系统的状态,还可以重构、匹配未知输入。将该设计方法应用于一类机器人系统,虽然系统未知输入初值和观测器重构的未知输入初值相差很大,但是观测器重构的未知输入值能够很快地跟踪上系统实际的未知输入值;虽然这是一种有界误差跟踪,但是误差可以控制在很小的范围内,并不影响实际应用。仿真结果表明,所提方法是有效的。

自适应观测器;代数建模;增广系统;未知输入重构

自适应观测器不仅可以跟踪系统的状态,还可以重构系统的未知输入,因而受到广泛的关注[1-3]。但是,文献[1-3]中的自适应观测器存在的充要条件之一是系统必须满足未知输入和可测输出之间的秩条件(也称为观测器匹配条件),而许多实际系统无法满足匹配条件。针对一类不满足匹配条件的线性时不变系统,文献[4]在文献[3]工作的基础上,通过设计辅助输出使得匹配条件得以满足。但是,辅助输出是不可测的,所以只能先通过设计高阶滑模微分器获取辅助输出的估计值,然后用这些估计值代替辅助输出的真实值,这使得观测器设计过程较为复杂。

对于一类不满足匹配条件的线性时不变系统,本文给出了一种不同于文献[4]的自适应观测器的设计方法。首先,通过使用代数建模的方法,将未知输入中不满足匹配条件的部分表述为一个动态系统,从而得到一个包含原系统和未知输入子系统的增广系统,这样的一个增广系统是满足匹配条件的;然后,证明了构建增广系统并不会破坏设计自适应观测器所需的其他充要条件;最后,针对该增广系统,设计了自适应观测器,用于状态观测和未知输入重构。相比于文献[1-3],当系统即使不满足匹配条件时,本文所提方法依然可以设计自适应观测器,用于观测状态和未知输入重构;相比于文献[4],本文所提自适应观测器设计方法比较简单、易于实现。但是,本文所提方法必须假设未知输入中不满足匹配条件的部分是确定的,且可以表述为自治动态系统的响应,这就需要对该部分故障有充分的了解,从而获取其统计特性。

1 系统描述和问题陈述

考虑线性时不变系统

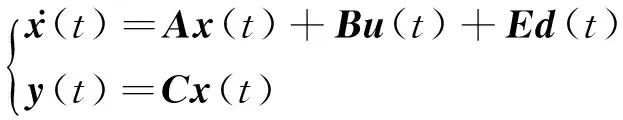
(1)

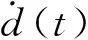
引理1[5]如果条件:①{A,E,C}的不变零点位于复平面的左半开平面;②rankE=rank(CE)(称为观测器匹配条件[6])成立,则对于某个正定阵Q∈Rn×n,存在矩阵L∈Rn×p、F∈Rq×p和正定阵P∈Rn×n使得

成立。

当式(1)满足引理1中的条件时,根据文献[3]可设计自适应观测器,即

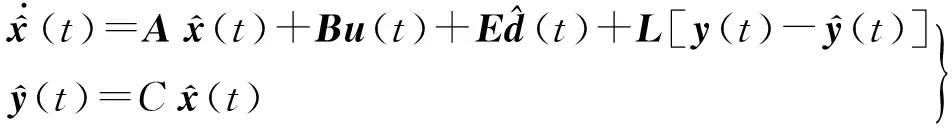
(2)

引理2[3]基于引理1中的条件,对给定的σ1,σ2>0,如果存在正定阵G∈Rq×q使得

成立(*为缺省值),则

(3)

使得ex(t)、ed(t)一致最终有界,式(3)中Γ>0是学习率。

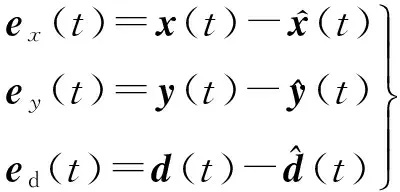
当引理1中的任意一个条件无法满足时,都无法设计式(2)、式(3)表示的自适应观测器。当式(1)满足引理1中的条件①,但是不满足条件②时,受文献[7-9]的启发,基于文献[4]辅助输出的估计值,给出了自适应观测器的设计方法,但获得辅助输出估计值的过程比较复杂。针对一类不满足匹配条件的线性时不变系统,文献[10-11]提出了降维和滑模观测器的设计方法,解决匹配条件不满足的主要手段是对不匹配未知输入进行代数建模。虽然系统的未知输入通常是不确定的,但是有一部分未知输入可以根据统计特性获知未知输入的数学模型。

本文希望基于对部分未知输入进行代数建模的方法,使得系统在满足引理1的条件①,但是不满足条件②的情况下,可以设计自适应观测器,故作出如下假设。

假设1 系统满足引理1中的条件①,但rank(E)≠rank(CE)。

2 自适应观测器的设计

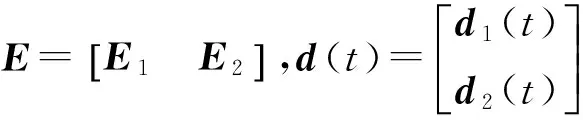
式(1)可以描述为

(4)

为了处理部分未知输入d2(t),作如下假设。

假设2 未知输入d2(t)可以表述为自治动态系统的响应。

基于假设2,使用文献[12]中的代数建模方法,通过选择合适的矩阵D∈Rδ×δ和H∈R(q-q1)×δ,可得

(5)

由式(4)、式(5)可得

(6)

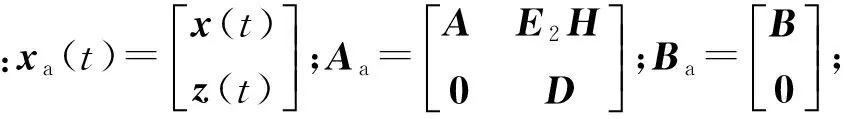
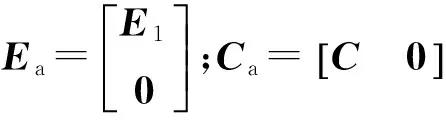
引理3[10]系统{A,E,C}、系统{Aa,Ea,Ca}的不变零点相同。

不难验证rank(Ea)=rank(CaEa)=q1成立,所以式(6)所示增广系统满足观测器匹配条件。由引理3可以看出,构建增广系统并不改变原系统的不变零点的位置。

引理3表明,当假设1成立时,{Aa,Ea,Ca}的不变零点依然位于复平面的左半开平面。由引理1可得以下定理。

定理1 基于假设1、假设2,对于某些正定阵Qa∈R(n+δ)×(n+δ),存在La∈R(n+δ)×p、Fa∈Rq1×p以及正定阵Pa∈R(n+δ)×(n+δ),使得

(7)

成立。

针对增广系统设计的自适应观测器为

(8)

由式(6)、式(8)可得

(9)

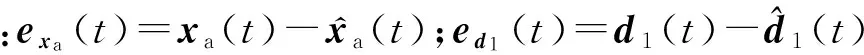
由引理2可以给出定理2。

定理2 基于假设1、2,对给定的θ1、θ2>0,如果存在正定阵Ga,使得

成立,则

(10)

使得exa(t)、ed1(t)一致最终有界。

根据定理2,重构匹配的未知输入为

(11)

虽然式(8)～式(10)所示的自适应观测器和式(2)、式(3)所示的自适应观测器在形式上相同,但是式(8)～式(10)所示的自适应观测器可以处理一些不满足匹配条件的系统,而式(2)、式(3)所示的自适应观测器只能处理满足匹配条件的系统。

当式(1)不满足匹配条件时,文献[4]提出了基于辅助输出的自适应观测器的设计方法。该方法可以避开匹配条件的限制,但是为了获取辅助输出的估计值,需要设计高阶滑模微分器,使得设计过程比较复杂,并且高阶滑模微分器的每一层都容易受到输出噪声的干扰。本文所提的基于代数建模的自适应观测器设计方法虽然必须对部分未知输入具有先验知识,但是方法简单,且易于实现。

3 仿 真

将所提的自适应观测器设计方法用于一个由直流电机驱动的一个机械手链接环节的模型[10]

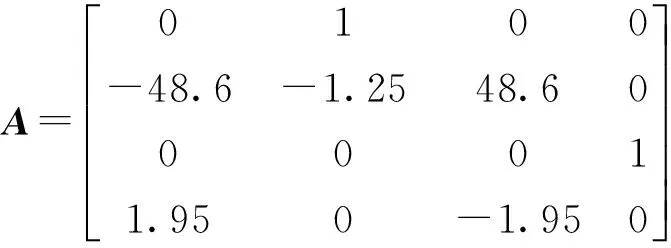
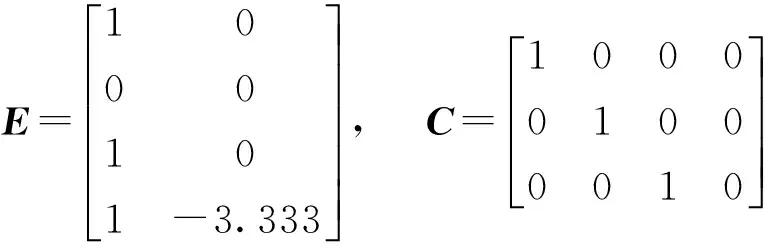
容易验证rank(CE)≠rank(E),如此以来,文献[3]中的自适应观测器设计方法将不再适用。当部分未知输入d2(t)是正弦信号sin(x2)时,可将故障矩阵E分解为E1和E2

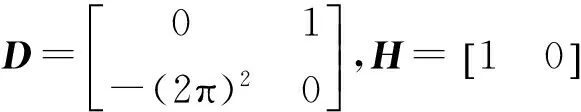
使用线性矩阵不等式工具箱,可得

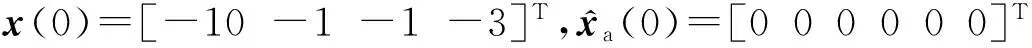
图1给出了匹配未知输入d1及其重构值。从仿真结果可以看出:虽然系统未知输入初值和观测器重构的未知输入初值相差很大,但是观测器重构的未知输入值能够很快地跟踪上系统实际的未知输入值;虽然是有界误差跟踪,但是误差可以控制在很小的范围内,并不影响实际应用。由此可见,本文所提的基于代数建模方法的自适应观测器可以很好地重构部分未知输入信号。

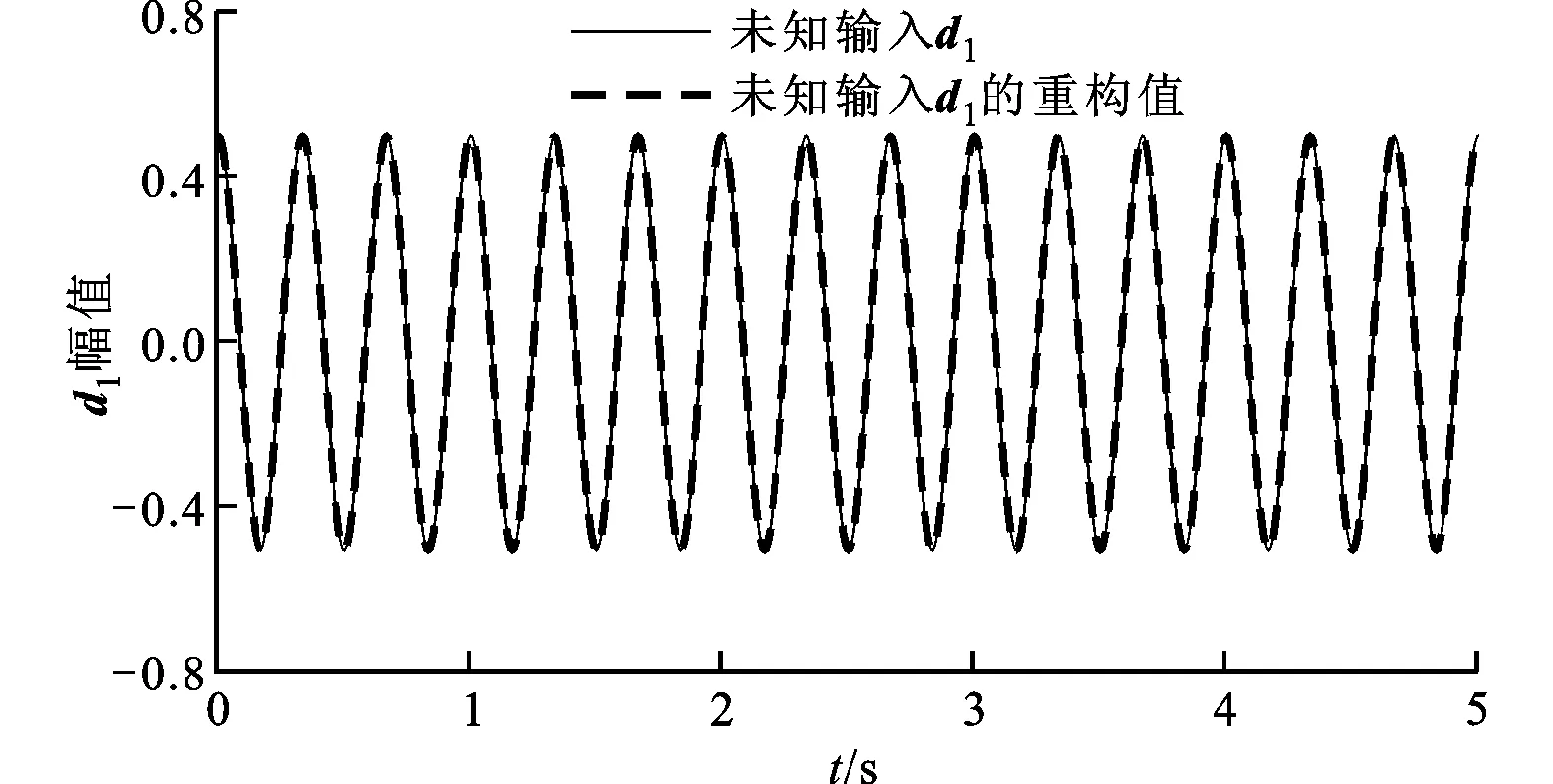
图1 未知输入d1(t)及其重构值

4 结 论

本文针对一类伴有未知输入的线性时不变系统,探讨了在观测器匹配条件不满足的情况下自适应观测器的设计问题。通过对部分未知输入进行代数建模,可以得到一类满足匹配条件的增广系统,并证明了在一定的条件下可以对该增广系统设计自适应观测器。仿真结果可以看出,本文所提的方法是有效的。

[1] ASTROM K J, WITTENMARK B. Adaptive control [M]. [s.l.]: Pearson Education North Asia Limited, 2003.

[2] YIN Shen, YANG Xuebo, KARIMI H R, et al. Data-driven adaptive observer for fault diagnosis [J]. Mathematical Problems in Engineering, 2012, 2012: 832836.

[3] ZHANG K, JIANG B, COCQUEMPOT V. Adaptive observer-based fast fault estimation [J]. International Journal of Control, Automation, and Systems, 2008, 6(3): 320-326.

[4] HAN Dong, LIANG Yueyong, YE Hao. Adaptive actuator fault estimation based on second-order sliding-mode differentiators [C/CD]∥The 25th Chinese Process Control Conference. Dalian, China: CPCC, 2014: 1-6.

[5] CORLESS M, TU J. State and input estimation for a class of uncertain systems [J]. Automatica, 1998, 34(6): 757-764.

[6] DRAZENOVIC B. The invariance conditions in variable structure systems [J]. Automatica, 1969, 5(3): 287-295.

[7] FLOQUET T, EDWARDS C, SPURGEON S K. On sliding mode observers for systems with unknown inputs [J]. International Journal of Adaptive Control and Signal Processing, 2007, 21(8/9): 638-656.

[8] KALSI K, LIAN J, HUI S, et al. Sliding-mode observers for systems with unknown inputs: a high-gain approach [J]. Automaitca, 2010, 46(2): 347-353.

[9] 韩冬, 朱芳来. 基于辅助输出的线性系统状态和未知输入同时估计方法 [J]. 自动化学报, 2012, 38(6): 932-943. HAN Dong, ZHU Fanglai. Simultaneous estimation of states and unknown inputs for linear systems based on auxiliary outputs [J]. Acta Automatica Sinica, 2012, 38(6): 932-943.

[10]PARK T G. Designing fault detection observers for linear systems with mismatched unknown inputs [J]. Journal of Process Control, 2013, 23(8): 1185-1196.

[11]汤承林, 练岚香, 刘俊. 基于代数方法的一类不确定系统的滑模观测器设计 [J]. 电子科技大学学报, 2015, 38(6): 932-943. TANG Chenglin, LIAN Lanxiang, LIU Jun. Sliding-mode observers design for uncertain systems based on an algebraic approach [J]. Journal of University of Electronic Science and Technology of China, 2015, 38(6): 932-943.

[12]ALBERTOS P, SALA A. Multivariable control systems: an engineering approach [M]. Berlin, Germany: Springer, 2004.

(编辑 赵炜)

Adaptive Observer Design Based on an Algebraic Modelling Approach

HAN Dong,LIU Jun

(Department of Automation, Tsinghua University, Beijing 100084, China)

This paper studies the problem of designing adaptive observers for linear time-invariant systems with unknown inputs when the observer matching condition is not satisfied. The unknown inputs are divided into two parts: one is matched and the other is mismatched. Under the assumption that the mismatched unknown inputs are deterministic and can be expressed as the response of a fictitious autonomous system, an augmented system consisting of the original system and the mismatched unknown inputs dynamical system is constructed so that the observer matching condition can be satisfied. For the augmented system, the procedure to design this adaptive observer is given, and it is able to not only observe the state of original system but also reconstruct the matched unknown inputs. Such adaptive observer is applied to a kind of robot system and the simulation results demonstrate the effectiveness of the proposed approach.

adaptive observer; algebraic modelling; augmented system; unknown inputs reconstruction

2014-11-24。作者简介:韩冬(1975—),男,博士,助理研究员。基金项目:国家自然科学基金资助项目(61203230)。

10.7652/xjtuxb201507015

TP13

A

0253-987X(2015)07-0088-04