基于遗传算法的下降阶段飞机油耗分析与研究

祝加雄

（乐山师范学院物理与电子工程学院，四川 乐山 614004）

基于遗传算法的下降阶段飞机油耗分析与研究

祝加雄

（乐山师范学院物理与电子工程学院，四川 乐山 614004）

为解决航班延误或机位冲突的情况下，飞机低空飞行和空中停留时油耗增加的问题，利用真实的飞行数据和遗传算法建立燃料消耗和高度之间的关系，设计具体的遗传算法实现数学模型的参数求解，从而得到最终的数学模型。在燃料消耗和高度之间建立指数模型，并对4个航班进行对比分析得到模型的相关系数。结果显示：可以用一个通用的指数模型对下降阶段燃料流量和高度之间的关系进行描述。

遗传算法；燃油消耗；下降阶段；飞行数据分析；数学模型

0 引 言

受诸多因素影响，航班延误及机位冲突不可避免，此时地面飞机需等待起飞，而飞行在空中的飞机则需要空中停留，这样会增加燃油消耗[1]。

遗传算法可用来优化飞行操作的各个方面。Kuroki等[2]研究了遗传算法在飞机到达机场及在跑道滑行等阶段制定明确时间规划的潜力。Omran等[3]运用先到先得方法对多跑道飞机到达机场后的排序和时序安排问题进行了研究。

除了飞行数据基础模型[4]，很少有人对飞机燃油消耗进行研究。本文运用遗传算法对飞机降落过程中燃料流量和飞行高度之间的关系进行评估，并通过飞机飞行数据记录获取110个有关燃料流量、飞行速度、引擎速度以及高度等真实数据（该数据来自土耳其珀加索斯航线2009次航班的原始数据）。此外，还分析了同种飞机和引擎产生的4次不同的降落情况，分析选用双引擎中程飞机B737-800。燃料流量和飞行高度之间的关系可用于目前最先进的航班延误管理系统[5]。当指定要在机场降落的飞机因特殊原因被迫停留在空中时，延误管理系统可向飞行员提供相应建议或相关故障信息[6-7]。考虑到飞机的性能、重量、风向、风速等客观因素，可以借助燃料流量和飞行高度模型将停留在空中的飞机引向更高的高度，这样相对于低空飞行可节省大量燃料[8-9]。因此，该研究对建立特定机型的飞行高度和燃油消耗关系具有一定指导意义。

1 遗传算法方案的建立

遗传算法是一种非常有效的工具，可用于研究线性或非线性模型[10]。算法方案包含5个模块。模块1确定该方案的特征，如航班号、数据观测范围、变量的上下限等。模块2根据每个染色体的实际计算值对所有染色体进行排序，该任务结束时，实际计算值为零的染色体将由最大实际计算值的染色体所取代。模块3和4中包含进行交叉和突变任务操作的代码。模块5将首次迭代的输出值记录在Excel空白表格中。

从F1航班飞机降落过程中燃料流量变化与飞行高度的对比中可以发现燃料流量呈指数下降，如图1所示。

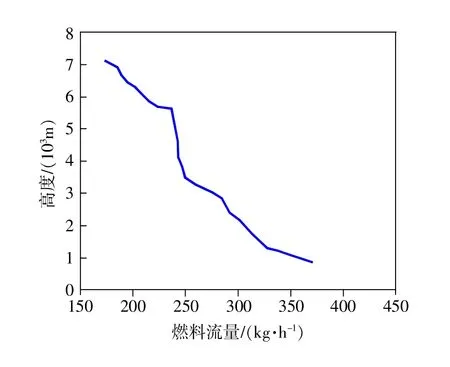
图1 F1航班下燃料流量和高度的变化关系

研究相应的模型需要用到指数函数，遗传算法可以确定该指数函数的各种系数。根据遗传算法，交叉率的假定参数值为0.4，突变率为0.02，首个系数α的精确度为10-6，第2个系数θ为10-8。选取如此低的值是为了能够为每个基因组提供足够敏感的位长，从而使两个系数都可获得敏感的变量。常规位长为30，α为1～1000，θ为-10-3～-10-7。母体值定为100。

2 分 析

使用遗传算法对4个航班进行运算。对目标函数的研究使用两种方法：

2.1 方法1

在该方法中，分别对所有的燃料流量和高度组（以下称为观测组）进行计算，从而使基础功能函数y最大化：

式中，k，j——航班号和观测组编号；

ff——燃料流量（以kg/h计）；

h——高度，m，通过飞行资料记录器记录；

α，θ——用来确定最佳输出值的系数。

航班F1至F4的观测组计算结果分别为28、20、19、18。在某特定高度，为实现剩余燃料流量最小化，需要获取y的最大值。在每个观测组中，遗传算法程序需要循环运行500次，而每一次都包括100个迭代。

由于每个航班的每个观测组都有不同的α和θ系数，故得到500个不同的y函数。在这种情形下，对航班F1而言，计算得到的500个α和θ值都是目标函数的输入值，所有的y函数输出值都需通过1/y计算来获得理想值，从而找到式（1）中分母的最小值。最后，观测组的最小余值都需通过计算余值的平方和获得。因此，能提供最小余值的α和θ系数便是最佳系数。

2.2 方法2

从第1个方法的结果可以看出，某一观测组的最大函数值与为所有观测组提供最佳系数的函数之间没有关系。因此在方法2中，使用不同的目标函数：

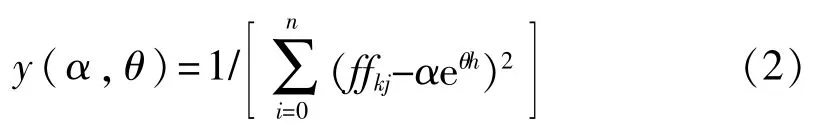
式中：i——观测组编号；

k——航班号；

n——每次航班观测组的数目。

式（2）能找到产生最大函数值的α和θ值，且能在最短时间得到最佳参数。

3 基于遗传算法的参数优化

为求解特定航班下燃料流量和高度之间的数学模型，设计了一种基于遗传算法的参数优化方法，算法描述如下：

输入：种群规模I=1000，子种群个数为5，预选择个体规模种群N，待求解参数α和θ，迭代次数t和最大值tmax，最优解未变化次数φ最大值δ。

输出：最优适应度个体。

1）将参数编码为二维的参数向量，并将其作为遗传算法中的染色体，随机初始化其值。

2）根据式（1）或式（2）计算所有个体的适应度值，根据轮盘赌选择概率，选择适应度较大的b个优良个体：

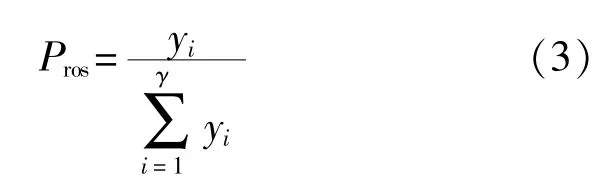
式中，γ为子种群的规模，可以看出，个体适应度yi越大，其被选择的概率越大。

3）采用两点交叉法对种群中的个体进行交叉和变异，直到生成规模由b增加到N。

4）根据式（1）或式（2）计算所有个体的适应度值，将其中具有最大适应度值的个体标记为最优个体。

5）判断最优个体的适应度是否高于上轮迭代中最优解的适应度，如果相等，那么φ=φ+1，否则φ=0。

6）判断当前迭代次数t是否已经达到最大迭代次数tmax或最优个体未变化次数是否已达到最大值δ，如果达到或者大于，则算法结束，输出当前最优适应度个体；否则t=t+1，返回步骤2继续进行迭代。

4 结果和讨论

根据分析，在第1种方法中，4次航班的每个观测组都运用遗传算法程序运算500次。该方法可以找出最大的函数值，以使相应观测组的余值最小。F4航班结果如表1所示。

从表1中可看出，对某些观测组而言，遗传算法可以为相应的y函数找到较大的输出值，这就使得该组的余值非常小。余值的最小平方和SSR下降时，模型的适应情况将改善。相应地，纵轴y函数便可产生最小余值平均和，但第4条数据除外，此处y函数所得值比较低。第6条数据中的余值平方和65.45是最小值，这个结果很好，它所允许的标准误差接近2.3kg/h。考虑到燃料流量在210～358kg/h范围内变动，标准误差的误差率仅为0.6%～1%。遗传算法程序的运算进程和相关余值在图2和图3中以迭代次数函数的形式表现出来。

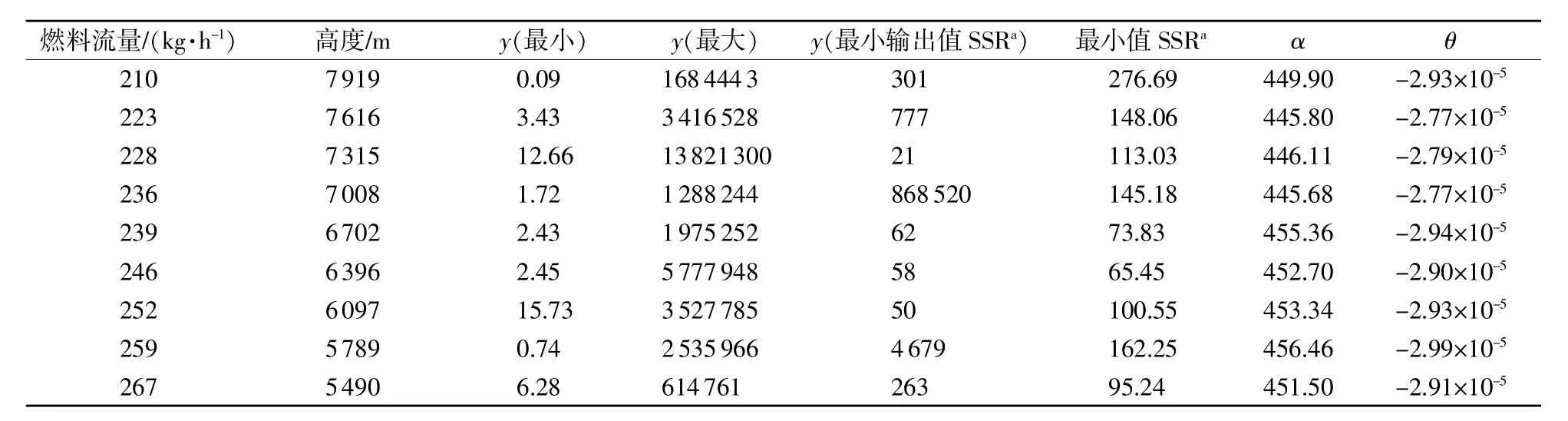
表1 对F4航班的每个观测组通过遗传算法计算程序采用式（1）计算所得的目标函数和系数值

在图2中，首次迭代的输出值是3.28，产生余值为0.3，而100次迭代后，输出值已接近5700000，而相应的余值为1.73×10-7。假使实际燃料流量为246kg/h，则首次迭代的输出值非常重要。输出值数量的增加意味着找到最佳答案概率的增加。

综合考虑F4航班的所有观测结果，可以从图3中看出使用产生最小余值平方和的系数（α=452.70，θ=-2.90×10-5）计算时，最大余值分别为3.65 kg/h和-3.00kg/h，比观测到的燃料流率小得多。对所有航班进行分析后，计算出最小余值平方和，如表2所示。对最小余值平方和而言，后两个航班值较低，而前两个航班值则相对较高。

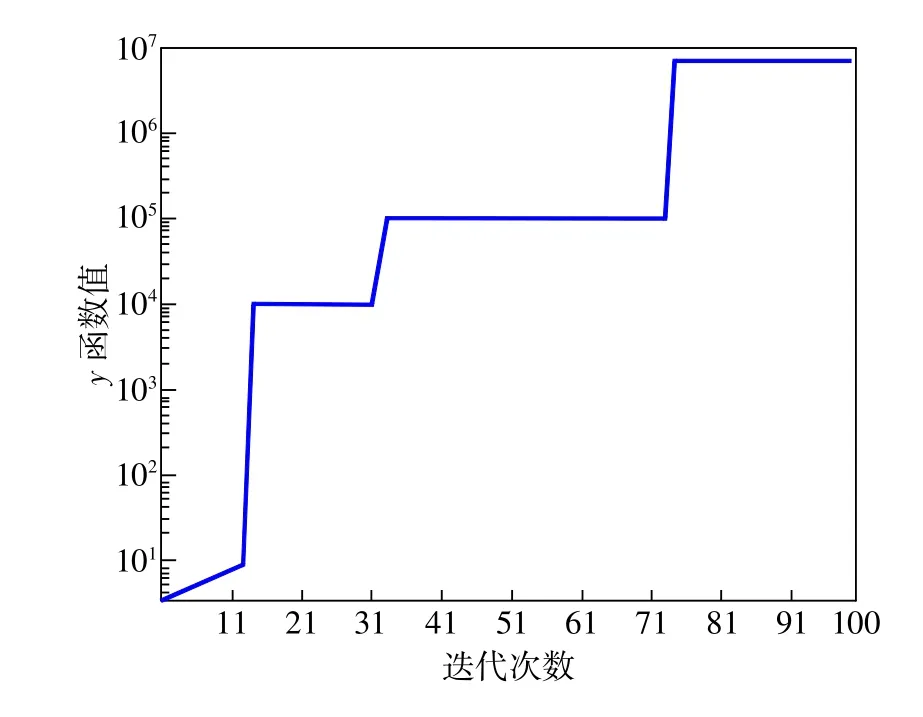
图2 运用遗传算法程序采用第一种方法对F4航班计算进程（燃料流率为246kg/h，高度为6396m）

在分析中，针对每次航班的观测组用遗传算法程序运算了500次。将每组500个不同的α和θ系数代入式（1）中，以确定可使飞行过程中余值平方和最小的α和θ系数值。图4展示了可使得所有4次航班中余值平方和最小的相应的α和θ系数值并给出了各观测组相应的值。

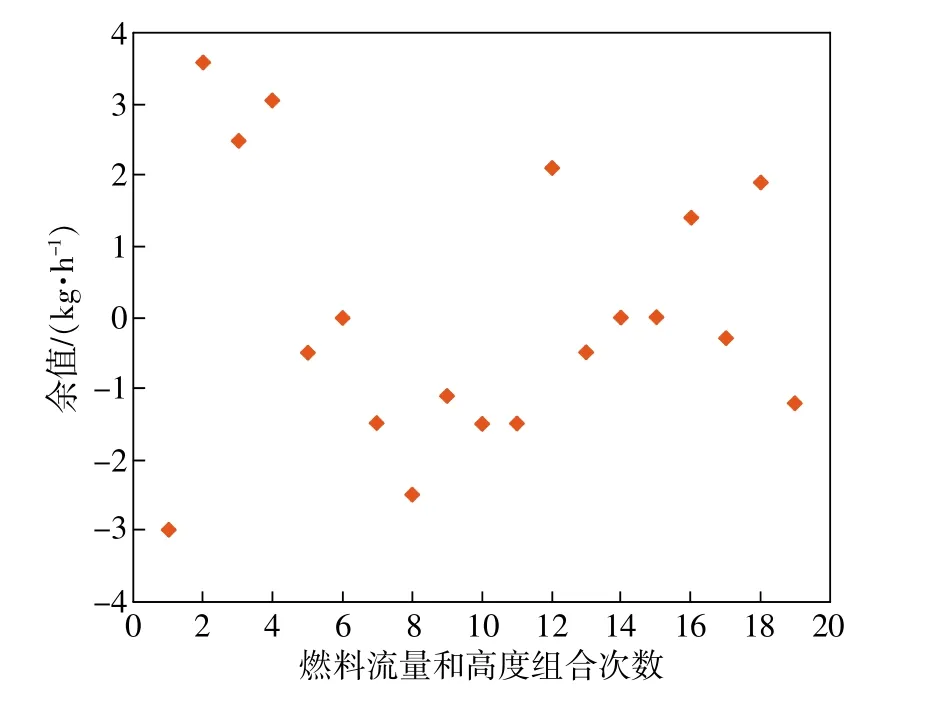
图3 采用公式（1）计算所得F4航班最小余值平方和（燃料流率为246kg/h，高度为6396m）

图4（a）显示的是F1航班中的误差区域对α系数的影响。该航班中，α的平均值约为441，计算包括这些区域的最低值（402）和最高值（518），这种明显的变化对标准误差造成了影响，使其增至28.9。在图4（b）中，α平方和余值的最小值约为813，而其他观测组的α值都使得标准误差变得更低（10.7）。F3和F4航班中的α系数值是接近的（见图4（c）和图4（d）。在图4（a）～图4（d）中，所有θ系数值都很接近。

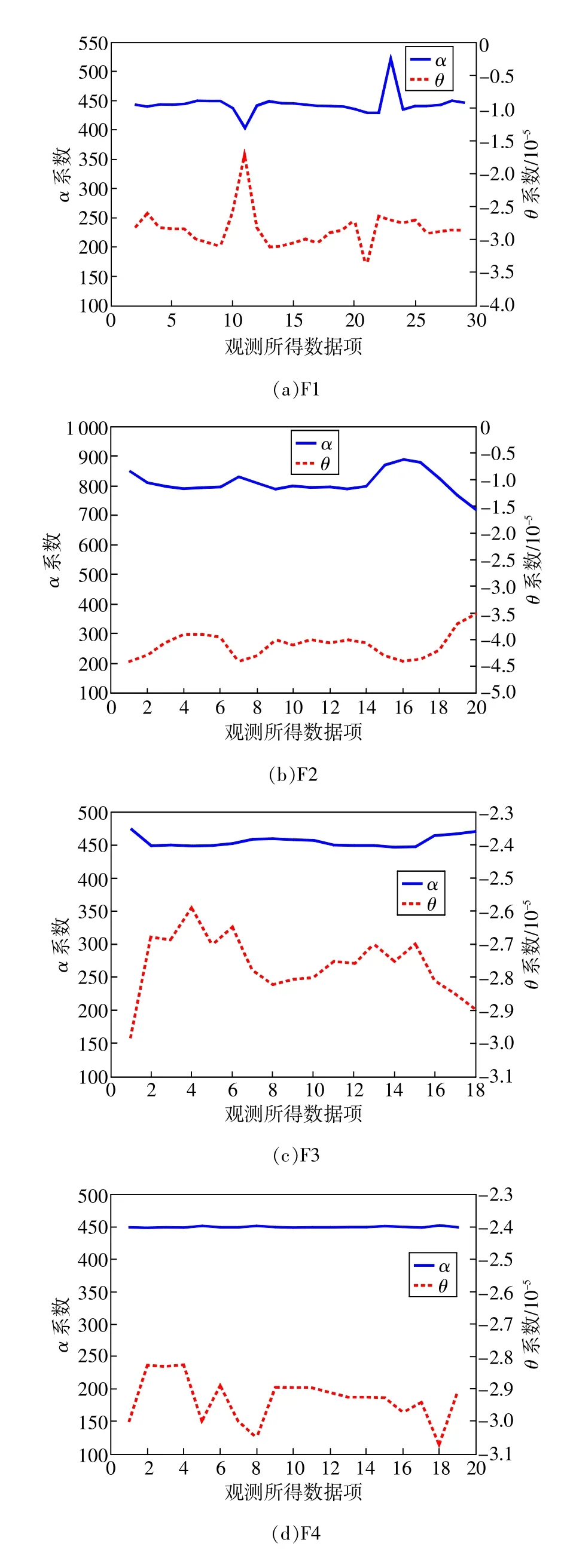
图4 根据第一种方法计算所有航班观测组所得结果作模型的系数,纵坐标表示可使最小平方和余值最小的系数

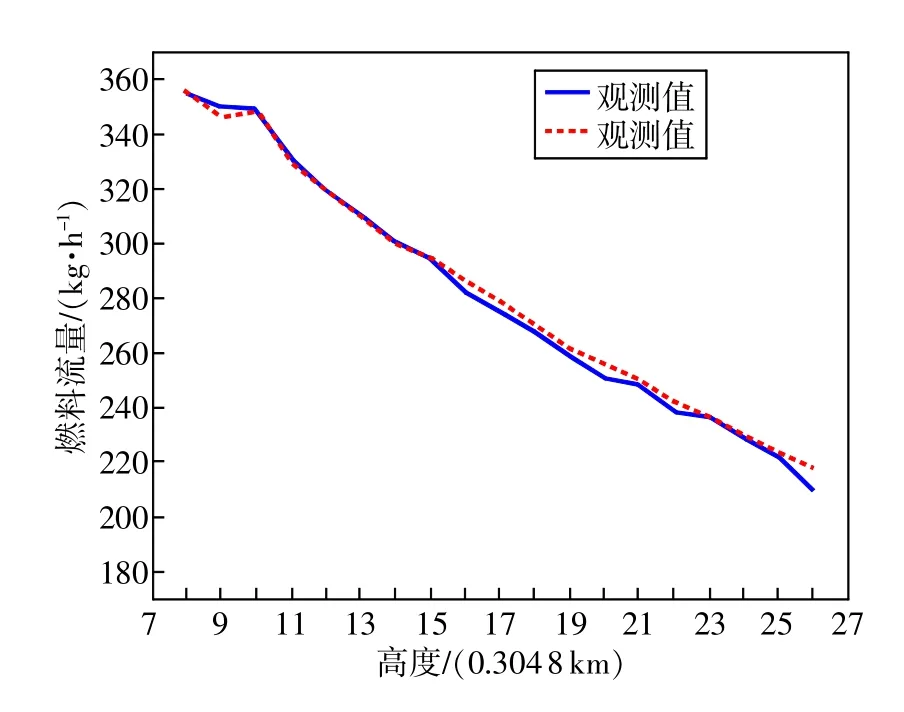
图5 燃料质量流率观测值和预测值比较

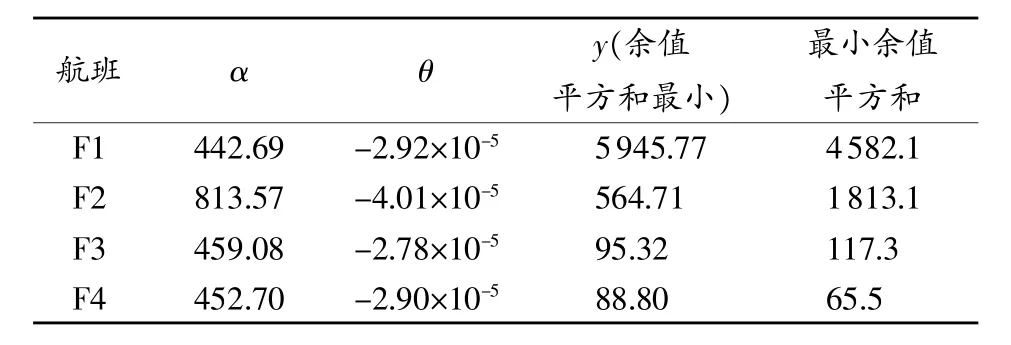
表2 采用第1个方法计算所得所有航班的最佳输出值

为了理解4个航班模型的意义，需要知道余值和实际观测值之间的关系。表2显示了F1～F4航班相应最小余值平方和。根据表2中的结果可以得出最大正余值和最小负余值与燃料质量流量之间的比率（以百分比计）为：F1航班中分别为+3%和-13%，F2航班中分别为+10%和-7%，F3航班中分别为+2%和-2%，F4航班中分别为+1%和-1%。前两个航班中的余值看起来非常高，而F1航班中的余值尤其高。该例中余值之所以较高，可能是因为观测到的燃料质量流量出现了偏差。

F3和F4航班中的结果比较接近，研究如何通过将F3航班中的系数用到F4航班的观测中（或将F4航班中的系数用于F3航班的观测中）来获取最小余值平方和。在将F3航班中的系数用到F4航班的观测中，所得最小余值平方和为203.1，在将F4航班中的系数用到F3航班的观测中，最小余值平方和为212.8。由于F3和F4航班中的最小余值平方和分别为65.5和117.3，则这两个航班余值平方和分别增加了225%和73%，且这种增加体现在余值与观测到的燃料质量流率的比率中。就与实际燃料质量流率的背离程度而言，第一种情形产生的结果更好。这种结果也显示出对配置相仿的航班而言，该模型都有意义。观测值和预测值之间的关系如图5所示。

第2个分析方法综合考虑了每次航班的所有观测组，则该模式可表述为式（2）的拓展公式：

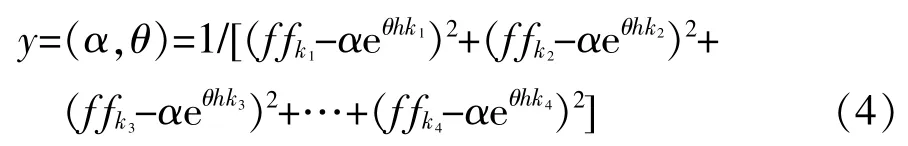
式中，k为航班号，目的是为每一航班确定其所有观测组的最小余值平方和。此方法下，遗传算法程序运算了1000次。母体和迭代均设为200。突变和交叉率保持不变。根据式（4）采用遗传算法程序计算所得的结果有力地证实了先前的推测。采用该方法所获取的最小余值平方和要比先前针对所有航班的相应预测值略低一些。输出值和相应系数见表3。

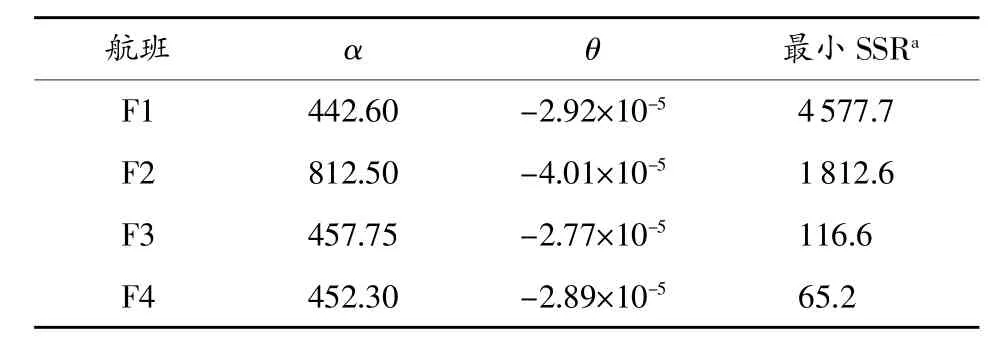
表3 根据式（4）采用第2种方法所得出的航班输出值

5 结束语

为了有效减少飞机运行过程的燃油消耗，在不影响飞机安全性的前提下，尽可能地提高燃油资源的利用率，提出了一种基于遗传算法求解目标函数参数的方法，并设计了具体的算法。通过大量实验表明，在飞机下降过程中，保持一个尽可能高的高度能更好地节约燃料，对垂直下降轮廓与燃料流量关系进行研究，可以直接对航空公司的总燃料节约潜力进行评估，同时也可以对着陆过程中燃料消耗所产生的环境影响进行评估，具有较大的可行性和现实意义。

[1]Gallar L，Arias M，Pachidis V，et al.Stochastic axial compressor variable geometry schedule optimization[J]. Aerospace Science and Technology，2011，15（5）：366-374.

[2]Kuroki Y，Young G S，Haupt S E.UAV navigation by an expert system for contaminant mapping with a genetic algorithm[J].Expert Systems With Applications，2010，37（6）：4687-4697.

[3]Omran A，Kassem A.Optimal task space control design of a Stewart manipulator for aircraft stall recovery[J]. Aerospace Science and Technology，2011，15（5）：353-365.

[4]刘婧.基于飞行数据分析的飞机燃油估计模型[D].南京：南京航空航天大学，2010.

[5]刘芳.下降阶段的飞机油耗优化建模方法研究[D].南京：南京航空航天大学，2012.

[6]刘君强，陈鹏超.基于航空公司飞机滑行油耗均衡原则的机场停机位分配算法[J].价值工程，2012，31（16）：3-4.

[7]熊杰，张晨.基于飞机滑行油耗的枢纽机场机位分配研究[J].交通运输系统工程与信息，2010，10（3）：166-170.

[8]张辉，王政元.浅谈低碳经济时代航空运输业的发展对策[J].空运商务，2011（2）：41-43.

[9]陈静杰，赵冬林.一种基于SVR的飞机巡航段油耗预测方法[J].航空电子技术，2014（1）：46-51.

[10]邱志平，张宇星.改进遗传算法在飞机总体参数优化中的应用[J].北京航空航天大学学报，2012，34（10）：1182-1185.

The research and analysis of fuel consumption based on genetic algorithm in aircraft decline phase

ZHU Jiaxiong
（School of Physics And Electronic Engineering of Leshan Normal University，Leshan 614004，China）

In the event of flight delay or flight conflict，the aircraft need flying low and stay in air，and the fuel flow rate increases rapidly.In order to solve this problem，the real flight data and genetic algorithm were researched to establish the relationship between the fuel consumption and the height of the flight.The specific gene algorithm was designed to accomplish parameter solving，so the final mathematical model was obtained.The exponential model between the fuel consumption and the height of the flight was established，and the four flights were analyzed to obtain correlation coefficients of the model.Results showed that the model can be used in a generic exponential model to describe the relationship between the fuel consumption and the height of the flight in aircraft decline phase.

genetic algorithm；fuel consumption；decline phase；flight data analysis；mathematical model

A

：1674-5124（2015）07-0124-05

10.11857/j.issn.1674-5124.2015.07.029

2014-12-10；

：2015-02-27

国家自然科学基金（61079022）

祝加雄（1982-），男，四川乐山市人，讲师，硕士，研究方向为模式识别与智能系统。