含径向双边裂纹圆环小试样的疲劳裂纹扩展试验方法

赵兴华，蔡力勋，包 陈

（西南交通大学力学与工程学院 应用力学与结构安全四川省重点实验室，四川 成都 610031）

含径向双边裂纹圆环小试样的疲劳裂纹扩展试验方法

赵兴华，蔡力勋，包 陈

（西南交通大学力学与工程学院 应用力学与结构安全四川省重点实验室，四川 成都 610031）

针对传统断裂测试试样受构型的限制往往尺寸较大，无法满足小尺寸金属管疲劳断裂行为测试要求的问题，设计新构型小尺寸试样。并基于有限元分析和柔度理论，建立含径向双边对称裂纹圆环（O-ring with double radial symmetric cracks，DOR）小试样的裂纹长度预测公式和应力强度因子公式，进而提出DOR小试样的疲劳裂纹扩展试验新方法。应用5083-H112铝合金加工成含径向裂纹小管试样和标准CT试样，开展疲劳裂纹扩展速率对比试验。结果显示，基于DOR试样得到的5083-H112铝合金的疲劳裂纹扩展规律与CT试样的试验结果相吻合，证明新方法的有效性。经过对试样端口的测量和分析，试样两侧对称裂纹的扩展量基本一致，说明对称裂纹满足唯一性要求，且不同于CT试样，该圆环试样裂纹前缘非常平直，表明圆环构型试样沿厚度方向的约束状态更加接近。

含径向对称裂纹圆环；疲劳裂纹扩展；柔度法；应力强度因子；有限元分析；材料试验

0 引 言

对于含裂纹的结构件，其疲劳裂纹扩展性能的表征通常采用传统的疲劳裂纹扩展试验方法[1-3]，即通过紧凑拉伸（compact tension，CT）试样以拉伸加载或用单边裂纹弯曲（single edged notch bending，SEB）试样以三点弯曲加载两类方式进行。由于CT试样需预留加载孔的位置，而SEB试样又需在跨距之间安装用于测量裂纹张开位移的位移计，使两类试样的标准尺寸均较大。随着薄板、薄壁管件[4-5]以及贵重金属零部件在航空航天、核反应堆、化工等工程中的广泛应用，使得特征尺寸在十几毫米甚至几毫米的小尺寸构件的断裂性能测试需求日益凸显。对于小尺寸管材而言，从中截取标准CT或SEB试样几乎不可能。此外，对于一些造价昂贵的特殊工程材料，采用标准试样必将大幅增加试验成本。因此，从小尺寸构件取样方便和有效降低试验成本两方面考虑，研究非标准小试样的疲劳裂纹扩展行为试验方法具有重要理论意义和工程应用价值。近年来，已有学者采用了C形环进行裂纹扩展研究，这种试样裂纹尖端的约束状态与真实管件的裂尖约束水平存在一定差异。

为了克服上述传统断裂测试试样存在的局限性，20世纪70年代，A.T.JONES等[6]对内表面含径向对称裂纹的圆环试样应力强度因子求解等基础问题进行过研究。其后，J.Ahmad[7]在前人研究的基础上，对此类构型试样的裂纹扩展应力强度因子进行了研究，G.Clark[8]利用残余应力理论和试验研究了厚壁圆筒的疲劳裂纹扩展。国内，马德林[9]较早研究了此类构型试样，他通过试验分析了应力强度因子的计算，但局限于同一种内外比值，只对a/t的变化进行了研究。其后，施惠基[10]利用圆环试样对304不锈钢偏心加载下的疲劳裂纹扩展行为进行了研究。

总体而言，国内相关研究较少，未形成简便易行的试验方法。因此，本文基于柔度法理论，建立内表面含径向对称裂纹的圆环试样柔度公式和K因子表达式，进而提出疲劳裂纹扩展试验方法并应用于反应堆管路材料5083-H112铝合金进行疲劳裂纹扩展行为研究。

1 试验条件

试验材料为5083-H112铝合金管材，表现出良好的镁、硅合金特性，具有优良的加工性、焊接性、电镀性、抗腐蚀性和高韧性，广泛应用于装饰、包装、建筑、运输、电子、航空、航天、兵器等行业，其主要化学成分见表1。

表1 5083-H112铝合金的主要化学成分

管材试样构型如图1所示，其中a为裂纹长度，t为管壁厚，r为内径，R为外径。试验在MTS809（25 kN）电液伺服材料试验机上完成，位移引伸计为MTS632.02F-20（标距D=5mm），载荷传感器和位移引伸计的准确度为0.5级。

图1 试样构型示意图

由于试件尺寸较小，无法在试件上安装引伸计，故本文设计了可以安装引伸计的专用压头，压头上装有可上下移动的刀片，刀片有两个螺栓固定于压头上，实验系统如图2所示。

图2 实验系统图

2 研究方法

2.1 裂纹扩展速率测试方法

裂纹长度的实时测试是疲劳裂纹扩展速率试验中的关键技术，常用方法有目测法、电位法和柔度法3类。柔度法是目前国标GB/T 6398——2000《金属材料疲劳裂纹扩展速率试验方法》中所推荐的主流测试方法[11]。该方法只需将试件尺寸、弹性模量及实时位移代入柔度公式即可获得当前循环下的疲劳裂纹长度。目前，SEB试样和CT试样已有成熟的柔度测试方法，本文将柔度方法拓展应用到小尺寸圆环试样，重点是获得内表面含径向对称裂纹的圆环试样（含径向双边对称裂纹小试样，DOR）的尺寸、应力强度因子和柔度的统一表达式。

2.2 有限元分析

考虑到试样对称性，建立如图3所示的1/2有限元平面的有限元模型，并对裂尖网格进行细化，单元类型为Plane182，弹性模量E=70GPa，泊松比ν=0.33。为了尽可能与试验过程相吻合，采用接触算法，建立两条刚性线来模拟上下压头，通过刚性线控制节点来施加位移荷载。有限元分析中提取的刚性线位移等效于试验中作动器夹头的位移，该位移与载荷的比值即为试样柔度C，随着裂纹长度的变化，试样柔度不断增大，相同载荷下的位移相应增大。

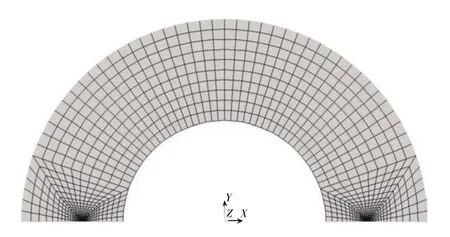
图3 平面有限元模型及网格划分

有限元计算的试件情况：6种内外径比W=r/R=0.5，0.55，0.6，0.67，0.7，0.75，其中每种半径比值下包含5种不同的内外径取值，每种取值下又选择若干裂纹长度。

2.2.1 基于柔度法原理的裂纹长度预测

为保证接触计算的准确性，对每个特定裂纹长度取10个不同位移步加载，对位移和载荷的有限元结果进行线性拟合获得含径向裂纹圆环的柔度C。通过该柔度可以建立下式所示的无量纲参量Ux：

式中：B——试样厚度；

E——弹性模量；

C——柔度系数。

裂纹长度a与厚度t之比a/t及无量纲变量Ux的有限元分析数据之间的关系如图4所示。

由图可知a/t和Ux之间表现出线性关系：

式中k1和b1为待定参数，式（2）的适用范围为0.3≤a/t≤0.65。不同内外径比下参数k1和b1的分析结果如表2所示。

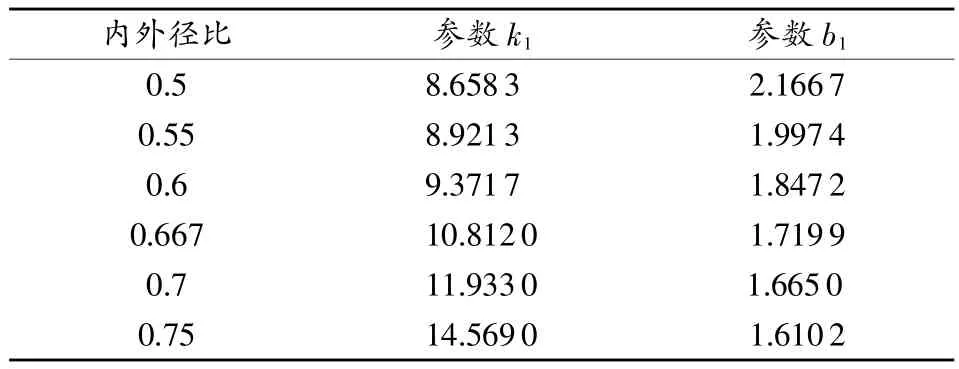
表2 不同内外径比下k1尧b1分析结果

将回归公式与有限元的计算结果进行对比分析，如图5所示，图中有限元得到的a/t与通过式（2）计算出的a/t的几乎所有数据点都分布在±2%的误差范围内，其中92%以上的误差在1.2%以内，表明式（2）有较高的准确度。

2.2.2 应力强度因子（K）公式

采用与分析柔度公式相近的方法对应力强度因子K进行无量纲处理，可得无量纲表达式f为

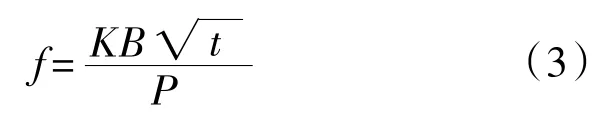
式中P为载荷，f与a/t的关系如图6所示。

由图可知两者亦存在线性关系：

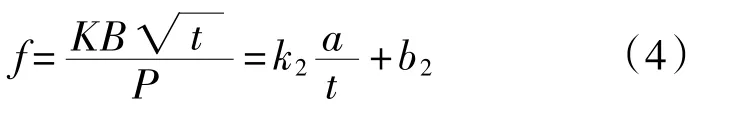
图4 不同内外径比下a/t与Ux的关系

图5 a/t有限元与公式结果对比

图6 不同内外径比下f与a/t的关系

式中k2和b2为待定参数，式（4）的适用范围为0.3≤a/t≤0.65，式（4）中不同内外径比下的参数变化如表3所示。

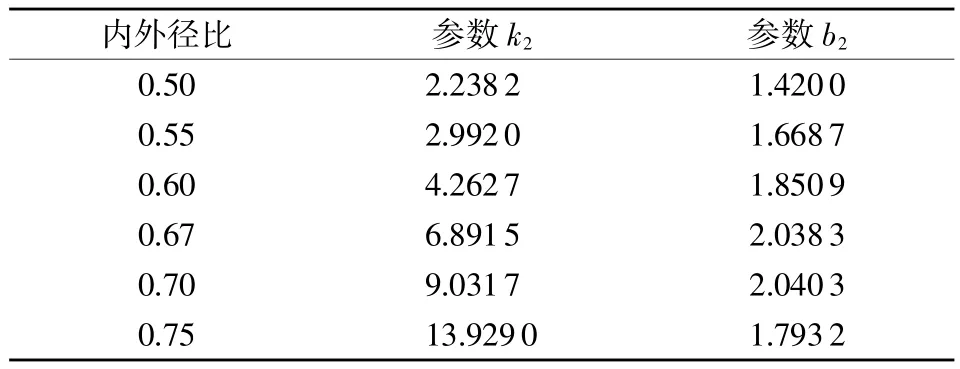
表3 不同内外径比下参数k2和b2的值

图7是有限元计算得到的应力强度因子K与回归式（4）计算得到的应力强度因子K的对比分析，图中所有数据点全部在±1.2%误差范围内，且90%的误差在±1%以内，表明式（4）有较高的准确度。

3 裂纹扩展速率试验结果

圆环试样尺寸：初始裂纹长度a=1 mm，内径r=5mm，外径R=10mm，壁厚t=R-r=5mm，宽度B=15mm；紧凑拉伸试样（CT）尺寸：试样宽度W=50mm，初始裂纹长度a=10mm。

表4 试样的Paris律模型参数

为了实时监测裂纹扩展速率，本文利用VB编写了计算软件，该软件可方便快速地计算裂纹扩展速度和扩展量。

图8为两个圆环试样（1#、2#）的裂纹长度a-循环次数N曲线，由图可见两试样的a-N曲线趋势一致。图9为两圆环试样与CT试样da/dN-ΔK曲线的对比，可见小圆环试样与CT试样的疲劳裂纹扩展速率基本一致，都分布在小的分散带内，说明此种构型的圆环小试样可以实现裂纹扩展速率的研究。

图7 应力强度因子K的有限元结果与公式计算结果对比分析

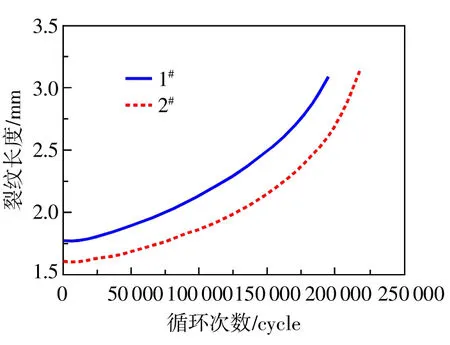
图8 圆环试样a-N曲线

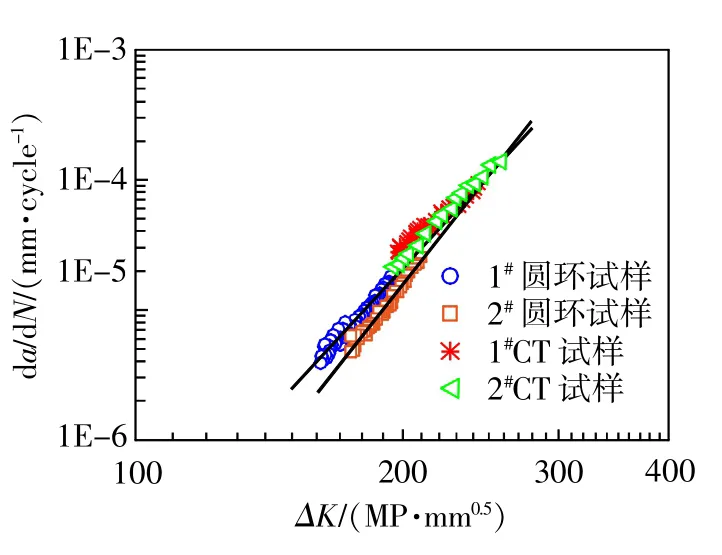
图9 疲劳裂纹扩展速率对比

材料的疲劳裂纹扩展速率的第2阶段一般满足Paris律关系：

式中C、m为材料常数，具体数值见表4。

图10给出了圆环试样1#、2#铝合金5083-H112管状疲劳裂纹扩展断面照片。图11是1#试样断口的局部放大图。

由图10可见，两试样上下两边的扩展量基本相等，且裂纹前缘接近一条直线，未出现CT试样常见的弧形前缘，说明该构型试样沿厚度方向的约束差异不大。

由图11可知，试样断面由线切割初始裂纹区、预制疲劳裂纹区、稳定扩展区及瞬断区组成，且区分较为明显。

图10只是定性反应了试样对称两侧扩展量基本相等，为了定量说明对称裂纹扩展量的一致性，可以利用金相显微镜通过9点法对裂纹扩展量进行测量，测量结果如表5所示，其中的a1、a2分别是上下两侧裂纹扩展量。

图10 圆环试样1#、2#断口对比图

图11 圆环试样1#的断口照片

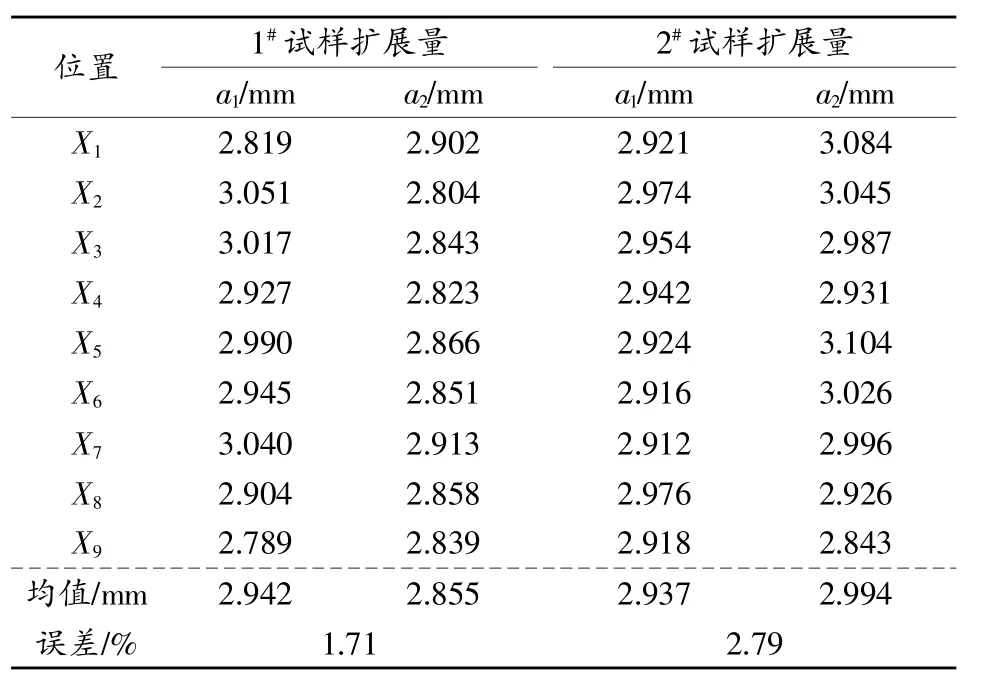
表5 圆环试样裂纹扩展量对比分析

由表5可知，两试样对称裂纹扩展量的差值均在3%以内，表明两个裂纹具有很高的对称性，可以用平均值进行表征，说明该构型试样的裂纹扩展具有唯一性。

4 结束语

1）基于线弹性有限元分析和柔度测试理论，建立了含径向裂纹管件的裂纹长度统一计算式，式中a/t和Ux呈线性关系，经验证公式具有较高的实测准确度。

2）基于线弹性有限元分析，建立了含径向裂纹管件的应力强度因子K的表达式，式中f与a/t亦呈线性关系，公式形式简洁，且满足准确度要求。

3）选用铝合金5083-H112完成了室温下的疲劳裂纹扩展速率试验。试验结果表明，相同规格管试样得到的疲劳裂纹扩展曲线分散性较小，并且与标准CT试样结果相吻合。

4）对称裂纹扩展量相等，满足裂纹扩展的唯一性，可以通过半对称模型进行简化分析。

5）铝合金5083-H112小圆环试样裂纹扩展前缘比CT试样更加平直，表明此种构型下裂纹处从内到外约束状态的差异较小。

[1]黄学伟，蔡力勋，包陈，等.基于低周疲劳损伤的裂纹扩展行为数值模拟新方法[J].工程力学，2011，28（10）：202-208.

[2]方钦志，张石山，赵明嗥，等.疲劳裂纹扩展柔度法测量系统研究[J].实验力学，2000，15（1）：110-114.

[3]Ding F，Feng M L，Jiang Y Y.Modeling of fatigue crack growth from a notch[J].International Journal of Plasticity，2007，23（7）：1167-1188.

[4]龚明，赵建华，董本涵，等.含孔薄板孔边疲劳裂纹的萌生和扩展[J].航空学报，2002，23（3）：202-205.

[5]郭加林，尹志民，王华，等.微量Sc和Zr对2524SZ合金薄板疲劳裂纹扩展特性的影响[J].中国有色金属学报，2010，20（5）：8278-8278.

[6]JonesA T.A radially cracked,cylindricalfracture toughness specimen engineering fracture mechanics[J]. Pergamon Press，1974（6）：435-466.

[7]Ahmad J，Ashbaugh N E.Constant KI crack-propagation test specimens[J].International Journal of Fracture，1982，19（2）：115-129.

[8]Clark G.Fatigue crack growth through residual stress fields-theoretical and experimental studies on thickwalled cylinders[J].Theoretical and Applied Fracture Mechanics，1984，2（2）：111-125.

[9]马德林.集中力加载下含径向裂纹圆环试样的K1解[J].兵器材料学与工程，1987（12）：6-11.

[10]Shi H J，Niu L S，Mesmacque G，et al.Branched crack growth behavior of mixed-mode fatigue for an austenitic 304L steel[J].International Journal of Fatigue，2000，22（6）：457-465.

[11]GB/T 6398—2000金属材料疲劳裂纹扩展速率试验方法[S].北京：中国标准出版社，2000.

Test method of fatigue crack propagation of small size O-ring with double radial symmetric cracks

ZHAO Xinghua，CAI Lixun，BAO Chen
（Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province，School of Mechanics and Engineering,Southwest Jiaotong University，Chengdu 610031，China）

Fatigue crack propagation behavior of small scale size tube founded in nuclear fuel cladding，aerospace equipment，and other fields widely，has great value for research.However，the traditionaltestspecimen is biggerrestricted by configuration， often can’trequire the requirements.To solve the problem which is mentioned above，a small scale size sample with a new configuration has been designed.Based on the finite element analysis and the compliance technique，a compliance formula and a stress intensity factor expression for the small scale size specimen O-ring configuration with double radial cracks（DOR）are proposed in the present study. A novel test method for fatigue crack propagation behavior of small scale size DOR according to the compliance technique has been developed.The aluminum alloy 5083-H112 was adopted to complete the fatigue crack propagation rate tests by using both the small scale size DOR and the standard CT.Results show that fatigue crack propagation rates for the small scale size DOR and the standard CT are close to each other and the validity of the method proposed was proved.The symmetrical cracks propagation quantity are almost the same on both sides of the sample through measurementand analysis ofthe fracture， itis show thatsymmetric cracks satisfies the requirement of uniqueness.And，different from CT specimen，the crack front of small scale size DOR is very straight，indicate that the small scale size DOR constraint condition is much closer along the thickness direction.

O-ring with double radial symmetric cracks（DOR）；fatigue crack propagation；compliance method；stress intensity factor；finite element analysis；material test

A

：1674-5124（2015）07-0001-05

10.11857/j.issn.1674-5124.2015.07.001

2015-02-01；

：2015-04-20

国家自然科学基金项目（11202174）四川省青年科技创新团队项目（2013TD0004）

赵兴华（1988-），男，山东泰安市人，硕士研究生，专业方向为疲劳与断裂力学。