熔渣粘度模型介绍及其预报效果比较

唐续龙，马明生

(中国恩菲工程技术有限公司，北京 100038)



熔渣粘度模型介绍及其预报效果比较

唐续龙，马明生

(中国恩菲工程技术有限公司，北京 100038)

本文介绍了几种常用的简单黏度模型及其计算参数(Riboud 模型,Urbain 模型，Iida 模型和NPL模型)，结合文献中报道的黏度数据，考察了各模型对不同渣系的预报效果。结果表明：Iida模型只适用于SiO2-CaO-K2O和SiO2-CaO-Na2O等少数渣系，其计算出的黏度值相比测量值具有较大的正偏差。NPL模型对不含Fe的渣系能取得一定的预报效果，但都有较大的正偏差。Ribound模型对含K2O、Na2O的渣系预报效果要好于其它模型。Urbain模型对常规的SiO2-Al2O3-CaO-MgO四元系及其子体系预报效果较好，经Alex等人修正后的Urbain模型对SiO2-Al2O3-CaO-FeO四元系及其子体系的预报都取得了很理想的效果。

黏度模型； 黏度； 熔渣

黏度是冶金熔渣的基本物理性质之一，与冶金过程关系密切，它涉及冶金过程的反应速度、金属与熔渣的分离、熔渣脱磷脱硫以及冶金操作的顺利与否等多方面的问题。在实际冶炼过程中，炉渣熔点高，成分复杂多变，使得测量出来的黏度数值并不能满足实际需求。长期以来，众多黏度模型被开发出来，在一定的成分和温度范围内有效地预报了冶金熔渣的黏度。这些模型主要可以分为两类：一种是结构模型，通过研究熔渣结构和黏度的相对应关系开发出来，如KTH模型[1]、似化学模型[2-5]等，此类模型适用范围较广，但模型参数较多，计算过程复杂，需借助专业计算机程序或者软件包进行计算；另一种是经验和半经验模型，如Urbain模型[6,7]、Ribound模型[8]、Iida模型[9,10]等，这些模型基于一定的数学算式，通过拟合实验数据获得模型的参数，对于拟合范围内的成分取得了较好的预报效果。本文介绍了几种常用的黏度模型及其参数，结合文献中报道的黏度数据，考察各模型对不同渣系的预报效果。

1 黏度模型介绍

1.1Riboud模型

Riboud模型[8]是一个纯经验模型，通过拟合大量的实验数据获得，应用范围较广。Riboud模型的黏度表达式基于Weymann-Frenkel (WF方程)液体动力学理论，根据式(1)来计算熔体的黏度：

μ=ATexp(B/T)/10

(1)

式中：μ为熔体的黏度(下同)，Pa·s；T为绝对温度(下同)，K；A为指前因子(下同)；B为黏滞活化能(下同)，J/mol。

Riboud模型将熔体的氧化物分为五大类，利用其摩尔分数计算A和B的值：

A=exp(-17.51+1.73XCaO+5.82XCaF2+7.02XNa2O-33.76XAl2O3)

(2)

B=31 140-23 896XCaO-46 356XCaF2

-39 159XNa2O+68 833XAl2O3

(3)

其中五类氧化物的摩尔分数计算方式为：

(1)XSiO2=XSiO2+XPO2.5+XTiO2+XZrO2；

(2)XCaO=XCaO+XMgO+XFeO1.5+XMnO+XBO1.5

(3)XAl2O3=XAl2O3

(4)XCaF2=XCaF2

(5)XNa2O=XNa2O+XK2O

1.2Urbain模型

Urbain模型也是基于WF方程形式，其黏度-温度关系可表示为：

μ=ATexp(1 000B/T)/10

(4)

-lnA=mB/1 000+n

(5)

Urbain通过拟合大量SiO2-MxO二元系的A、B，获得m和n的值分别为0.29和11.57。Urbain模型将组成熔体的氧化物分为三大类，利用其摩尔分数(三类氧化物归一化后的摩尔分数)计算B的值，三类氧化物分别表示为：

(1) 酸性氧化物：XG=XSiO2+XP2O5

(2) 碱性氧化物：XM=∑XMxO

(3) 两性氧化物：XA=XAl2O3+XB2O3

黏滞活化能B通过式(6)、式(7)和式(8)来计算：

BM=B0+B1XG+B2(XG)2+B3(XG)3

(6)

(7)

(8)

利用式6、7和8计算不同碱性氧化物的BM，利用式9计算体系的总活化能B：

(9)

Urbain提供的二元系(SiO2-MxO)和三元系(SiO2-Al2O3-MxO)的参数如表1和表2所示。

表1 二元体系参数

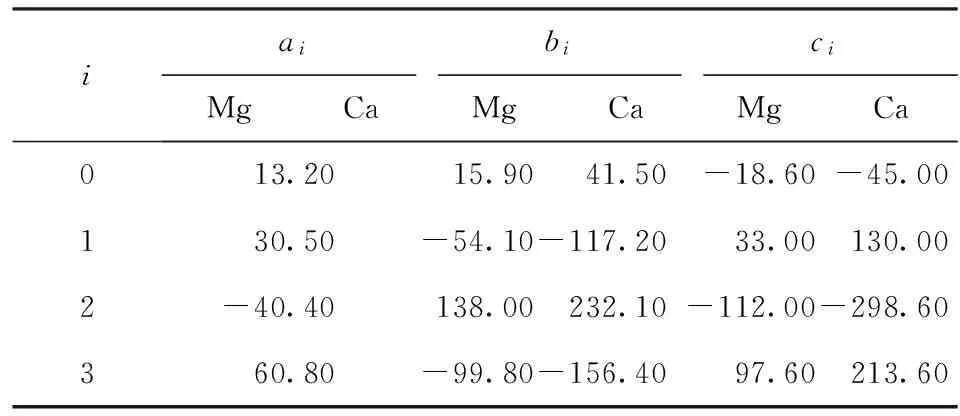
表2 三元体系参数

Alex等人[11]将Urbain模型中的m表示为纯氧化物mi的叠加，并将修正后的Urbain模型应用于SiO2-Al2O3-CaO-FeO四元系的黏度预报，取得很好的预报效果。修正后的模型参数如表3所示，修正后的m值表式为：

m=∑miXi

(10)

式中mi为纯氧化物的m值，Xi为纯氧化物在熔体中的摩尔分数。

表3 Alex修正的Urbain模型参数

1.3Iida模型

Iida等人[9,10]将熔体的碱度指数与其结构关联起来，通过式11-式17计算熔体黏度，模型的相关参数如表4所示。

(11)

A=1.745-1.962×10-3T+7.000×10-7T2

(12)

E=11.11-3.65×10-3T

(13)

(14)

(15)

(16)

(17)

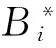
表4 Iida模型参数

(18)

a=1.20×10-5T2-4.355 2×10-2T+41.16

(19)

b= 1.40×10-7T2-3.494 4×10-4T+0.206 2

(20)

c=-8.00×10-6T2+ 2.556 8×10-2T-22.16

(21)

1.4NPL模型

Mills[12]认为熔体的光学碱度跟其结构有所关联，可以用于计算熔体的黏度。在硅铝酸盐熔体中，考虑到部分阳离子需参与[AlO4]5--四面体电荷平衡而形成[1/2MxAlO4]4-结构，且具有较大阳离子半径的氧化物拥有优先权，需要对光学碱度的计算进行修正：

(22)

式中：Xi为第i组元修正后的摩尔分数；ni为第i组元的氧数目；Λi为第i组元的光学碱度，如表5所示。

NPL模型的黏度计算式为：

(23)

参数A和B与温度T无关，都是修正后的光学碱度Λ的函数：

(24)

A=-232.69(Λ)2+357.32Λ-144.17

(25)

表5 部分氧化物的光学碱度

2 黏度模型预报

众多的黏度模型中，准化学模型和KTH模型的计算过于复杂，且未给出相应的模型参数；CSIRO模型和Tanaka模型需借助专业的计算机软件包计算三种氧的摩尔分数。基于上述原因，本文选择以Riboud模型、Urbain模型、Alex等人修正的Urbain模型、NPL模型和简化的Tanaka模型[13]作为比较对象，比较数据来自已报道的黏度数据，包括二元系、三元系及多元系。

为了考察预报效果，利用式26和27来计算预报误差：

相对误差

(26)

平均误差为

(27)

3 黏度模型效果比较

各黏度模型对熔渣黏度的预报效果如表6和图1所示。

由图1和表6可以看出，Iida模型只对SiO2-CaO-K2O和SiO2-CaO-Na2O等少数体系的预报误差低于25%，对大部分体系的预报误差都在50%以上，个别体系的预报误差甚至超过1 000%，这说明Iida模型计算出的黏度值相比测量值具有较大的正偏差。NPL模型对SiO2-MnO和SiO2-CaO-MgO体系的预报误差小于25%，大部分体系的预报误差都位于25%～100%之间，对SiO2-FeO、SiO2-CaO-FeO和SiO2-MgO-FeO少数体系的预报误差超过100%而呈现明显的正偏差。Ribound模型对大部分体系的预报效果都较差，但对含K2O、Na2O的体系预报效果要明显好于其它模型。Urbain模型对常规的SiO2-Al2O3-CaO-MgO四元系预报效果较好，对该四元系及其子体系的预报误差均在25%以内，但对于其它体系的预报效果则很一般，尤其是对含K2O、Na2O的体系预报误差甚至超过100%。Alex等人对Urbain模型进行适当修正后给出了SiO2-Al2O3-CaO-FeO四元系的参数，修正后的Urbain模型对SiO2-Al2O3-CaO-FeO四元系及其子体系的预报效果很理想，在25%以内，对SiO2-CaO-FeO三元系的预报误差甚至小于10%。

表6 各黏度模型的预报效果

注：1.“空白”表示无法计算；2.“—”表示误差超过1 000%；3.处理FetO时将Fe2O3当FeO处理，即1 mol Fe2O3折合成1.5 mol FeO；4.Si-SiO2；Al-Al2O3；Ca-CaO；Mg-MgO；Fe-FeO；Fet-Fe2O3与FeO共存；Mn-MnO；K-K2O；Na-Na2O；Li-Li2O；Sr-SrO；Ba-BaO。

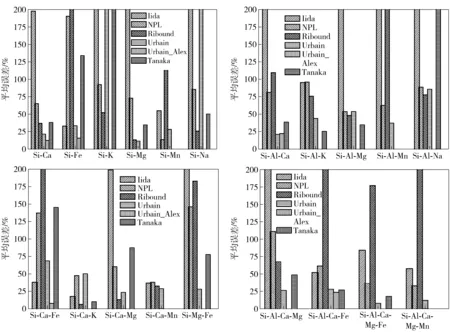
图1 各黏度模型预报效果

3 结论

本文介绍了常用的黏度模型计算方法及参数，根据文献报道的黏度数据对各模型的预报效果进行了比较，计算结果表明：

(1) Iida模型和NPL模型的预报较测量值具有较大的正偏差，应用范围较窄，仅限于少量简单体系。

(2) Ribound模型对大部分体系的预报效果都较差，但对含K2O、Na2O的体系预报效果要明显好于其它模型。

(3) Urbain模型对常规的SiO2-Al2O3-CaO-MgO及其子体系都能取得较好的预报效果，应用范围较广。

(4) Alex等人修正后的Urbain模型对SiO2-Al2O3-CaO-FeO四元系及其子体系的预报效果都在25%以内，对SiO2-CaO-FeO三元系的预报误差甚至小于10%，取得了非常好的效果。

[1] Sichen D,Bygden J,Seetharaman S.Model for estimation of viscosities of complex metallic and ionic melts[J].Metallurgical and Materials Transactions B:Process Metallurgy and Materials Processing Science,1994,25(4):519-525.

[2] Kondratiev A,Hayes P C,Jak E.Development of a quasi-chemical viscosity model for fully liquid slags in the Al2O3-CaO-′FeO′-MgO-SiO2system[J].Part 1.Description of the model and its application to the MgO,MgO-SiO2,Al2O3-MgO and CaO-MgO sub-systems.ISIJ International,2006,46(3):359-367.

[3] Kondratiev A,Hayes P C,Jak E.Development of a quasi-chemical viscosity model for fully liquid slags in the Al2O3-CaO-′FeO′-MgO-SiO2system[J].Part 3.summary of the model predictions for the Al2O3-CaO-MgO-SiO2system and its sub-systems.ISIJ International,2006,46(3):375-384.

[4] Kondratiev A,Hayes P C,Jak E.Development of a quasi-chemical viscosity model for fully liquid slags in the Al2O3-CaO-′FeO′-MgO-SiO2system[J].Part 2.A review of the experimental data and the model predictions for the Al2O3-CaO-MgO,CaO-MgO-SiO2and Al2O3-MgO-SiO2systems.ISIJ International,2006,46(3):368-374.

[5] Kondratiev A,Hayes P C,Jak E.Development of a quasi-chemical viscosity model for fully liquid slags in the Al2O3-CaO-′FeO′-MgO-SiO2system[J].The experimental data for the ′FeO′-MgO-SiO2,CaO-′FeO′-MgO-SiO2and Al2O3-CaO-′FeO′-MgO-SiO2systems at iron saturation.ISIJ International,2008,48(1):7-16.

[6] Urbain G.Viscosity of liquid silica-alumina-Na and K oxides.Measurements and estimations[J].Revue Internationale des Hautes Temperatures et des Refractaires,1985,22(1):39-45.

[7] Urbain G,Millon F,Cariset S.Viscosities of some silica rich liquids in the system SiO2-B2O3[J].Comptes Rendus Hebdomadaires des Seances de l′Academie de Sciences,Serie C (Sciences Chimiques),1980,290(8):137-140.

[8] Riboud P V,Roux Y,Lucas L D,et al.A experimental study on the binary silicate systems[J].Fachber.Huttenprax.Metallweiterverarbei,1981,19：859-869.

[9] Iida T,Sakai H,Kita Y,et al.Equation for estimating viscosities of industrial mold fluxes[J].High Temperature Materials and Processes,2000,19(3):153-164.

[10] Iida T,Sakai H,Kita Y,et al.An equation for accurate prediction of the viscosities of blast furnace type slags from chemicalcomposion[J].ISIJ International,2000,40(Supplement):S110-114.

[11] Kondratiev A,Jak E.Review of experimental data and modeling of the viscosities of fully liquid slags in the Al2O3-CaO-′FeO′-SiO2system[J].Metallurgical and Materials Transactions B:Process Metallurgy and Materials Processing Science,2001,32(6):1015-1025.

[12] Mills K C.Influence of structure on the physico-chemical properties of slags[J].ISIJ International,1993,33(1):148-155.

[13] Nakamoto M,Miyabayashi Y,Holappa L,et al.A model for estimating viscosities of aluminosilicate melts containing alkali oxides[J].ISIJ International,2007,47(10):1409-1415.

[14] Mills K C,Chapman L,Fox a B,et al.′Round robin′ project on the estimation of slag viscosities[J].Scandinavian Journal of Metallurgy,2001,30(6):396-403.

[15] Yasukouchi T,Nakashima K,Mori K.Viscosity of ternary CaO-SiO2-Mx(F,O)yand CaO-Al2O3-Fe2O3melts[J].Tetsu-To-Hagane/Journal of the Iron and Steel Institute of Japan,1999,85(8):571-577.

[16] Kucharski M,Stubina N M,Toguri J M.Viscosity measurements of molten Fe-O-SiO2,Fe-O-CaO-SiO2,and Fe-O-MgO-SiO2slags[J].Canadian Metallurgical Quarterly,1989,28(1):7-11.

[17] Ji F Z,Sichen D,Seetharaman S.Experimental studies of the viscosities in the CaO-FenO-SiO2slags[J].Metallurgical and Materials Transactions B:Process Metallurgy and Materials Processing Science,1997,28(5):827-834.

[18] Machin J S,Yee T B.Viscosity Studies of System CaO-MgO-Al2O3-SiO2:IV,60 and 65% SiO2[J].Journal of the American Ceramic Society,1954,37(4):177-186.

[19] Scarfe C M,Cronin D J.Viscosity-temperature relationships of melts at 1 atm in the system diopside-albite[J].American Mineralogist,1986,71(5-6):767-771.

[20] Scarfe C M,Cronin D J,Wenzel J T,et al.Viscosity-temperature relationships at 1 atm in the system diopside-anorthite[J].American Mineralogist,1983,68(11-12):1083-1088.

[21] Sykes D,Dickinson J,James E,et al.Viscosity-temperature relationships at 1 atm in the system nepheline-diopside[J].Geochimica et Cosmochimica Acta,1993,57(6):1291-1295.

[22] Kawahara M,Mizoguchi K,Suginohara Y.The viscosity and the infrared spectra of CaO-SiO2-MnO and MnO-SiO2-Al2O3melts[J].Bulletin of the Kyushu Institute of Technology (Science and Technology),1981(43):53-59.

[23] Segers L,Fontana A,Winand R.Viscosities of melts of silicates of the ternary system CaO-SiO2-MnO[J].Electrochimica Acta,1979,24(2):213-218.

[24] Ji F Z,Sichen D,Seetharaman S.Experimental studies of viscosities in FenO-MgO-SiO2and FenO-MnO-SiO2slags[J].Ironmaking and Steelmaking,1998,25(4):309-316.

[25] Urbain G,Bottinga Y,Richet P.Viscosity of liquid silica,silicates and alumino-silicates[J].Geochimica et Cosmochimica Acta,1982,46(6):1061-1072.

[26] Williams P,Sunderland M,Briggs G.Viscosities of synthetic slags in the system CaO-′FeO′-SiO2-MgO[J].Transactions of the Institution of Mining and Metallurgy,Section C:Mineral Processing and Extractive Metallurgy,1983,92:c105-c109.

[27] Johannsen F,Brunion H.Untersuchungen zur Viskosität von Rennschlaken[J].Zeitschr.Erzbergbau und Metallhuttenwesen,1959,12(6):272-279.

[28] Kim J R,Lee Y S,Min D J,et al.Influence of MgO and Al2O3contents on viscosity of blast furnace type slags containing FeO[J].ISIJ International,2004,44(8):1291-1297.

[29] Machin J S,Yee T B.Viscosity studies of system CaO-MgO-Al2O3-SiO2:II,CaO-Al2O3-SiO2[J].Journal of the American Ceramic Society,1948,31(7):200-204.

[30] Machin J S,Yee T B,Hanna D L.Viscosity Studies of System CaO-MgO-Al2O3-SiO2:Ⅲ,35,45,and 50% SiO2[J].Journal of the American Ceramic Society,1952,35(12):322-326.

[31] Bills P M.Viscosities in silicate slag systems[J].Journal of the Iron and Steel Institute,1963,201(2):133-140.

[32] Higgins R,Jones T J B.Viscosity characteristics of rhodesian copper smelting slags[J].Bulletin of the Institution of Mining and Metallurgy,1963,682:825-864.

A description of slag viscosity model and the prediction capability

TANG Xu-long,MA Ming-sheng

The present paper described several commonly used viscosity model and the model parameters (Riboud model,Urbain model,Iida model and the IPL model).Combined with the viscosity data reported in the literatures,the capability of each viscosity model to different slags was assessed.The results showed that:Iida model is only suitable for a small amount of slag systems,such as SiO2-CaO-K2O and SiO2-CaO-Na2O,with large positive deviations compared with measured values.NPL model can predict a good result for slags without iron oxide,but has a larger positive deviation.Riboud model has a better forecast results for slag containing K2O,Na2O than other models.Urbain model has a better forcast results for conventional SiO2-Al2O3-CaO-MgO quaternary system and its sub-systems than other models.After being modified by Alex,very satisfactory forecast results can be obtained for the SiO2-Al2O3-CaO-FeO quaternary system and its sub-systems.

viscosity model; viscosity; slag

唐续龙(1984—)，男，博士研究生，工程师，从事有色冶金设计、咨询类工作。

2014-03-19

TF02

A

1672-6103(2015)01-0018-06