基于FPGA 的高阶FIR 滤波器设计

焦淑红，智 扬

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

有限冲击响应(Finite Impluse Response，FIR)数字滤波器是数字信号处理领域中最基本的元器件之一，FIR 滤波器具有工作稳定、结构简单、相位严格线性等特点，因而得到了广泛应用。随着科学技术及工程实践的发展，人们对滤波器性能的要求越来越高，如高频率分辨率，高阻带衰减等。这些指标的提升导致FIR滤波器的阶数越来越高。目前采用软件实现高阶FIR滤波器无法实现并行处理，不利于提高系统的实时性，而采用专用的滤波器芯片虽然有速度高、工作稳定的优点，但是灵活性较差。

FPGA 是专用集成电路领域的一种半定制电路，可构建高度并行的数据处理架构，提高系统的实时性［1］。而FPGA 的可重配置性意味着只要开发出算法，便可通过下载不同的配置文件对相应硬件结构和功能进行升级，这也保证了系统有更强的适应性和灵活性。FPGA 不仅具有专用集成电路速度快和工作稳定的特点，又兼具了软件的实时性，是实现高阶FIR 滤波器的理想器件。

本文采用FPGA 实现高阶FIR 滤波器，介绍了快速卷积结构的FIR 滤波器原理［2］和一维转二维FFT算法来实现长序列的FFT［3］，给出了FPGA 上各模块的结构原理和仿真验证结果。

1 FIR 滤波器原理及FFT 算法改进

1.1 快速卷积结构原理及运算量分析

FIR 滤波器的输出可用时域上的线性卷积y(n)=h(n)*x(n)实现。若两序列x(n)与h(n)的长度分别为N1和N2(N1≠N2)，将两序列补零变成L 点的序列x'(n)和h'(n)，且满足

就可用两序列的圆周卷积代替两序列的线性卷积。利用“时域序列的圆周卷积等效于频域的离散频谱的乘积”这一性质，可先对两L 点序列进行离散傅里叶变换(DFT)［4］

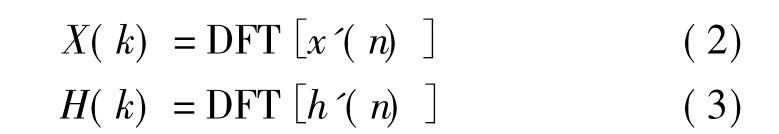
两者相乘，得到

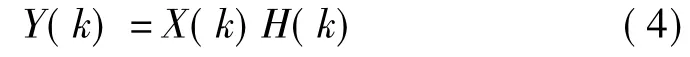
最终再对Y(k)进行离散傅里叶反变换(IDFT)

图1 快速卷积结构示意图

对于快速卷积结构，将x(n)与h(n)均补零变成长度为L 的序列，则快速卷积结构需要进行(L+1)log(L)次复数乘法和2Llog(L)次复数加法。

随着FIR 滤波器［6－7］的阶数增加，采用线性卷积等方法的运算量会急剧增加，而采用快速卷积结构可大幅减小运算量，当N1和N2足够长时，用该结构计算线性卷积更快，这对提高滤波器的实时性有着重要的意义。

1.2 FFT 算法改进

对于高阶的FIR 滤波器［8－9］，由于输入序列补零后长度较长，采用直接级联型的方法实现长序列FFT会造成存储规模过于庞大，逻辑设计也较为困难，必须加以改进。

设输入序列x(n)的长度N=2n，其DFT 为

式(5)中0≤k ＜N，将输入序列按间隔l 等间距抽取，l是2 的幂次方数。

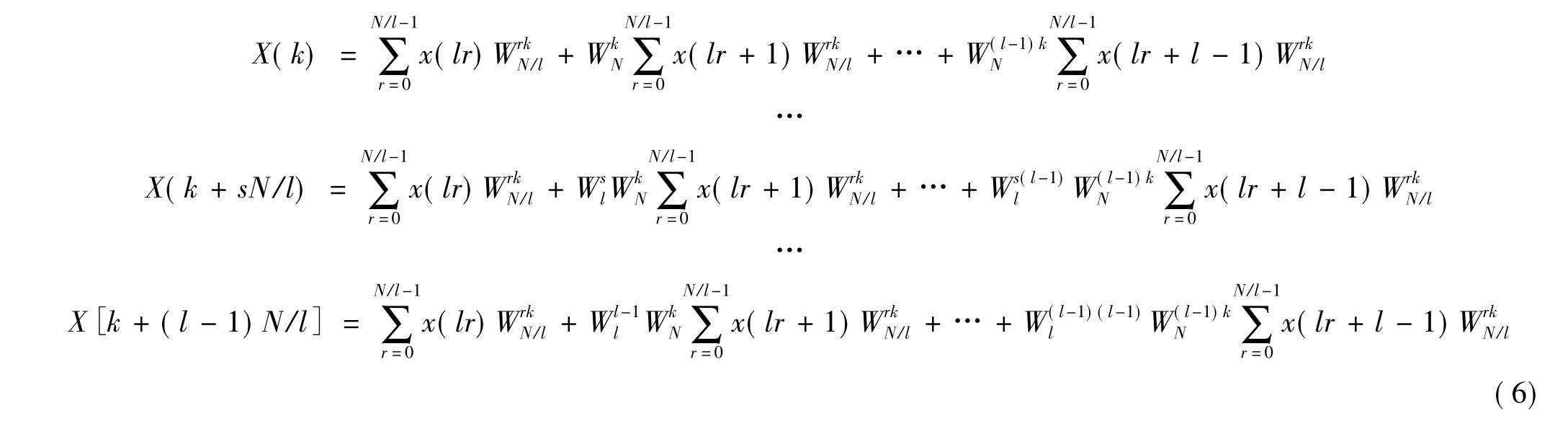
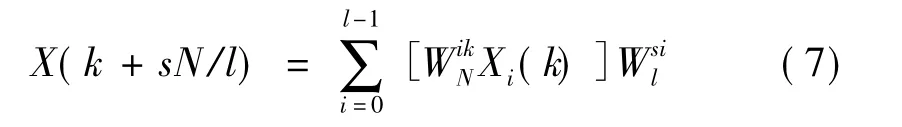
2 FPGA 实现高阶FIR 滤波器

系统使用Xilinx 公司的XCLVLX240T FPGA，采用Verilog HDL 语言进行算法设计。

如图2 所示，当系统开始工作时，控制模块将FFT/IFFT 模块、频域相乘模块［11］等各部分的复位端口拉高1 000 ns 使各模块复位。复位操作完成后，FFT/IFFT 模块从存储器1 中读取输入序列进行FFT变换。FFT 变换完成后的数据直接送入频域相乘模块中，频域相乘模块从滤波器系数存储器中读取系数与FFT 结果相乘，并将相乘结果存入存储器1 中。频域相乘运算结束后，控制模块对各模块进行复位，复位完成后，FFT/IFFT 模块从存储器1 中读取数据进行IFFT变换，得到滤波器输出结果，并将结果重新存储在存储器1 中。

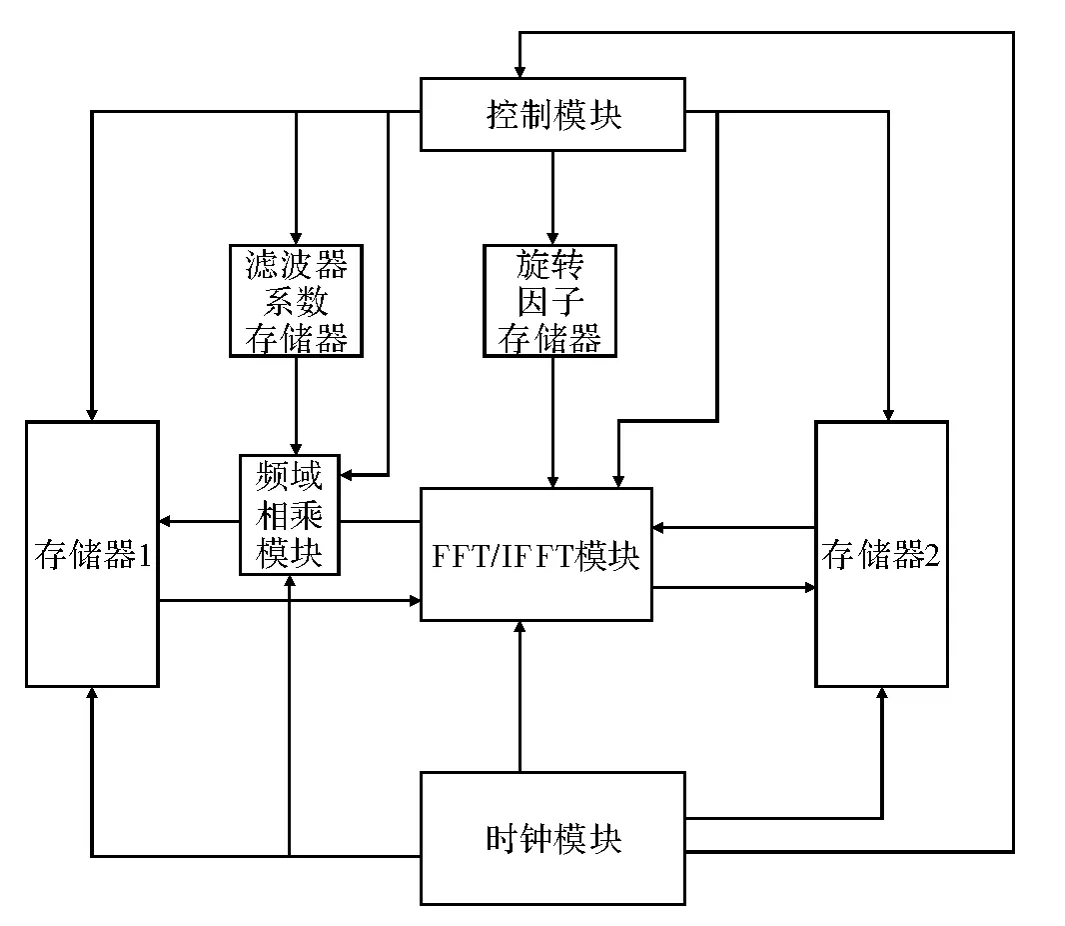
图2 FIR 滤波器系统模块组成示意图

2.1 FFT/IFFT 模块设计

FFT/IFFT 模块在进行FFT 时从存储器1 中读取列数据，送入128 点列变换FFT 核中，FFT 核的输出连接到复数乘法器，与旋转因子相乘后送入存储器2 暂存。列变换完毕后，256 点行变换FFT 核从存储器2中读取数据进行行变换，并输出最终的FFT 运算结果。IFFT 过程与FFT 过程类似，只是在读取旋转因子时，对旋转因子的最高位，即符号虚部符号位的最高位取反，得到FFT/IFFT 模块内部的连接框图如图3所示。

2.2 频域相乘模块设计

频域相乘模块的作用是从系数存储器中读取滤波器系数并与FFT 的输出相乘，得到频域的乘积结果。频域相乘模块包括地址控制单元和复数乘法器两部分，其内部连接如图4 所示。

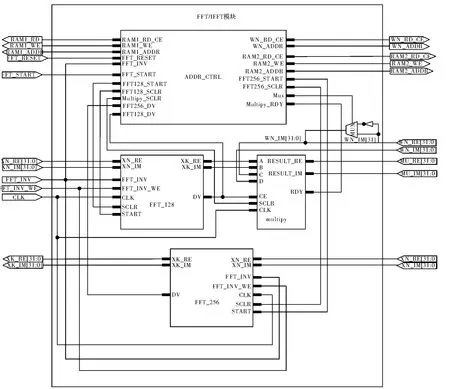
图3 FFT/IFFT 模块内部结构图

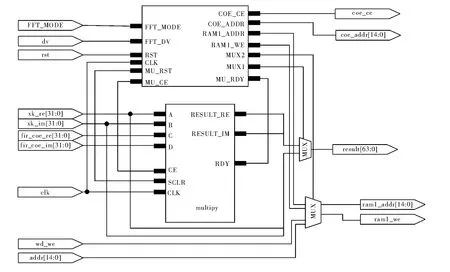
图4 频域相乘模块结构图

如图4 所示，当FFT_MODE 信号为低电平时，系统工作在IFFT 状态下，复数乘法器不启动，FFT/IFFT模块输出数据xk_re 与xk_im 通过多路选择器直接连接到存储器1 的数据输入端口，FFT/IFFT 模块输出的写使能信号和地址信号也通过多路选择器直接连接到存储器1 的写使能端口和地址端口。

当FFT_MODE 信号为高电平时，系统工作在FFT状态下。控制单元输出系数存储器地址信号和读使能信号，与xk_re、xk_im 相乘。当复数乘法器RDY 信号拉高时，控制单元输出存储器1 的地址信号和写使能信号，并通过多路选择器连接到存储器1 相应的端口，频域相乘结果存入存储器1 中。

3 实验结果

本文采用Matlab 对FPGA 进行辅助设计和仿真验证，表1 是FIR 滤波器的设计指标。

表1 FIR 滤波器设计指标

根据上述指标，通过Matlab 的FDATool 采用凯塞窗设计得到一个15 056 阶的带通FIR 滤波器，并产生测试数据x(t)=0.5sin(270×2πt) +2sin(40×2πt)。测试数据与滤波器系数补零成为32 768 点序列，并对补零后的滤波器系数进行FFT。将这两组数据写入.coe 文件中，连同设计文件下载到FPGA 中。基于FPGA的高阶FIR 滤波器仿真输出波形如图5 所示。

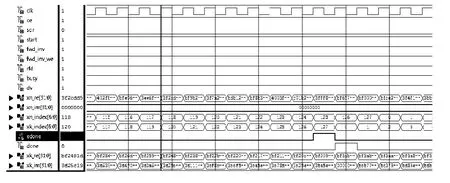
图5 基于FPGA 的高阶FIR 滤波器仿真输出波形

仿真软件ISIM 将仿真输出数据存储在.txt 文件中，Matlab 读取.txt 文件并绘制图形得到如图7 所示的结果。

图6 测试数据波形

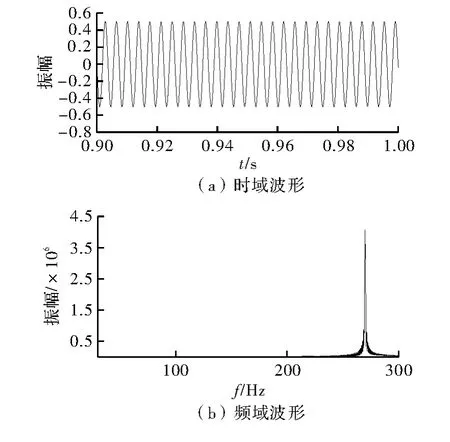
图7 FPGA 仿真输出结果

由图可看出，测试数据中包含的40 Hz 频率成分已经完全被滤除，只保留了270 Hz 的频率成分，可见基于FPGA 的高阶FIR 滤波器完全可达到设计要求。在速度方面，基于FPGA 的高阶FIR 滤波器在200 MHz 工作时钟下完成滤波操作只需1.5 ms，速度超过了Matlab。

4 结束语

本文详细叙述了基于快速卷积的FIR 滤波器原理，并推导了一维大点数FFT 转二维小点数FFT 的公式，给出了基于FPGA 的高阶FIR 滤波器的工作过程和FFT/IFFT 模块等关键模块的结构原理及工作过程。仿真验证表明，采用快速卷积结构实现高阶FIR 滤波器可大幅减少运算量，达到实时处理的效果。采用一维大点数FFT 转二维小点数FFT 的方法可以有效减少FPGA 片内存储资源的消耗，并降低了逻辑控制的复杂性。相比Matlab，FPGA 能做到实时处理，且误差可控制在较小的范围内，是实现高阶FIR 滤波器的有效手段。

［1］ 王志超.基于FPGA 的低通滤波器［D］.哈尔滨:哈尔滨理工大学，2012.

［2］ Meher P K.New approach or look－up－table design and memory－based realization of FIR digitial filter［J］.IEEE Circuits and Systems Scoiety，2010，57(3):592－603.

［3］ 赵忠武.32 位浮点FFT 专用信号处理器设计［D］.北京:北京理工大学，2003.

［4］ Cheng Hansung.Design and implementation of a scalable fast fourier transform core［J］.IEEE Transactions on Cricuit，2002，78(6):63－67.

［5］ Johanson S，Shousheng He，Nilson P.Wordlength optimization of a pipelined FFT processor Circuit and Systems［C］.Lanzhou:42ndMidwest Symposium on Cricuit，2000:501－503.

［6］ 蒋垒，王昌林，刘鎏，等.基于FPGA 的FIR 数字滤波器算法实现［J］.舰船电子工程，2006(1):151－156.

［7］ 刘刚，林志远，王毅增.基于流水线的并行高效FIR 滤波器设计［J］.电子技术应用，2003(7):60－62.

［8］ 唐治德，刘敏，刘晓明.用高密度可编程逻辑器件实现参数化FIR 滤波器［J］.重庆大学学报:自然科学版，2002，25(3):72－74.

［9］ 高耀鸿.基于FPGA 的FIR 低通滤波器［D］.长沙:湖南大学，2012.

［10］高振斌，陈禾，韩秋月.可变2n 点流水线FFT 处理器的设计与实现［J］.北京理工大学学报，2006，26(4):338－341.

［11］石碧，程维综，何晓雄.16X16 位带符号无符号基于RTL级的可综合的高速乘法器［J］.电子工程师，2003，29(6):58－62.