落叶松人工林直径分布动态预估模型1)

赵丹丹 李凤日 董利虎

(东北林业大学，哈尔滨，150040)

责任编辑:王广建。

林分直径分布规律是国内外林学家和林业工作者关注和研究的重点。许多学者对林分直径结构分布模型进行了大量研究。总体上可分为基于现实林分的静态模拟和基于未知林分的动态模拟。静态拟合指利用概率密度函数(如正态分布、负指数分布、SB分布、β分布、Γ分布和Weibull分布等)来描述林分直径分布结构［5-9］;动态模拟指运用转移矩阵、参数预测和参数回收等［10-13］方法，建立林分直径结构动态预测模型，进而准确的描述和揭示林分直径分布的动态变化规律。国外学者对直径分布的动态已有研究［14-15］，Qin J．H．等［15］将枯损率和直径生长方程加入模型中，通过不同的建模方法，寻找一种可以将全林分模型或单木模型与径阶模型相连的最优模型。国内相关研究较少，孟宪宇等［16］将长白山落叶松林地按地位级指数划分为3个地位等级，分别建立3参数Weibull分布的直径分布收获模型;李梦等［17］认为林龄、平均胸径、地位指数、密度是影响直径分布的主要因子;段爱国等［18］利用固定样地的观测数据，采用偏度、峰度、直径变动系数、径阶株数分布及累积直径频率作为指标，对杉木人工林林分直径结构动态变化规律及其密度效应进行了探讨。总之，传统的直径分布模型的研究，对后期概率密度函数的参数没有限制，且在模型拟合时，没有考虑参数间的内在相关性。本研究利用小兴安岭及长白山地区两期(10 a间隔期)落叶松人工纯林102块固定样地的复测数据，基于改进的参数预测模型，将林分平均直径、Weibull分布参数等作为自变量，以后期直径分布的Weibull参数作为约束条件，采用似乎不相关回归(SUR)理论估计参数，构建实质上的直径分布动态预测模型，并对模型的预估精度进行检验，为森林抚育与森林可持续经营提供有效的数据与理论支持。

1 研究区概况

本研究地区为小兴安岭地区(127°42'～130°14'E，46°28'～49°21'N)和长白山地区(126°40'～131°16'E，41°35'～47°57'N)。小兴安岭地区海拔为600～1 000 m，长白山地区海拔为800～1 500 m。两个地区都属温带季风气候，有明显的大陆性气候特征，四季分明，冬长夏短，其土壤主要为暗棕壤。小兴安岭地区年平均气温0℃，年降水量为550～670 mm;长白山地区年平均气温-2℃，年降水量为600～900 mm。落叶松人工纯林树种组成为10落。

2 研究方法

2．1 数据来源

本研究数据来源于长白山地区和小兴安岭地区设立的不同立地条件、不同密度和不同海拔的102块兴安落叶松人工纯林样地。该样地均符合Weibull分布，且所有样地在10 a间未经过任何采伐。在这102块样地中，59块来自长白山地区，43块来自小兴安岭地区;样地面积为0．06或0．1 hm2;兴安落叶松人工纯林固定标准地的调查数据间隔期为10 a;前期数据和复测数据的样地数都为102块。各标准地林分调查因子的统计量见表1。

表1 落叶松人工纯林林分调查因子及其Weibull分布参数统计表

2．2 偏度与峰度

偏度(SK)是用于衡量分布的不对称程度或偏斜程度的指标，而峰度(ST)是用于衡量分布的几种程度或分布曲线的尖峭程度的指标。偏度和峰度经常被用来描述林分直径分布特征［19-20］。

由偏度和峰度的计算公式可知，当SK＞0时为正偏斜或右偏;当SK＜0时为负偏斜或左偏，其绝对值越大则偏斜程度越大;当SK=0时为正态分布。当ST＞0时表示分布比正态分布更集中在平均数周围，分布呈尖峰状态;当ST＜0时表示分布为比正态分布更分散，分布呈低峰态;当ST=0时分布为正态分布。

Current Situation and SWOT Analysis of Greenbelt System in Pingquan City_____________________________LI Jiaqi,YUAN Liwei,LIU Yang 33

2．3 Weibull分布

2．3．1 分布函数

Bailey等［5］首次将Weibull分布应用到林业领域中，在研究林分结构方面显示出较大的灵活性与较强的实用性。其概率密度函数为:

其中，DBH为胸径，a为位置参数，即最小径阶的下限值。b为尺度参数，b值越大，密度函数曲线越平缓，顶点到横坐标轴的距离越小。c为形状参数，当1＜c＜3．6时，Weibull分布呈山形曲线，且为正偏;当c＜1时，为倒“J”型分布;当c=1时，为指数分布;当c=2时，为卡方分布;当c=3．6时，为近似正态分布;当时c＞3．6时，为山型负偏;当c→∞时，Weibull分布变为单点分布。由此可见，Weibull分布通过c值的改变可以拟合成各种形式的直径分布，尤其对人工林，可拟合任何时刻的林分直径分布，且参数a、b、c随年龄的变化呈现出一定的规律性。3个参数中，c是关键参数，Weibull分布就是通过c值的变化来灵活用于各种分布类型。

2．3．2 理论径阶株数计算

确定概率密度函数的参数a、b、c后，可以得到其累积概率密度函数F(DBH)，因此，理论径阶株数ni可按下式求得［21］:

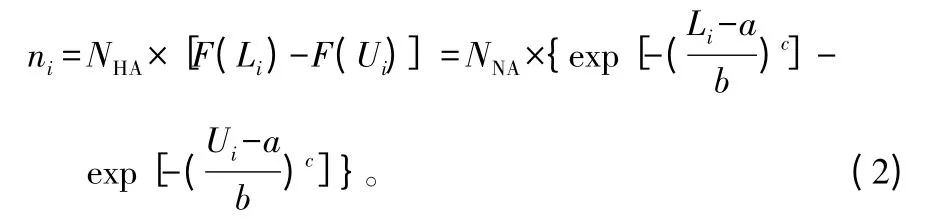
其中，Ui、Li分别为第i径阶的上、下限;NHA为总株数;F(DBH)为累积概率密度函数。

2．3．3 拟合优度

在本研究中，直径分布拟合优度评价采用以下两个指标，相对误差(B)和误差指数，来进行评价。其计算公式为:

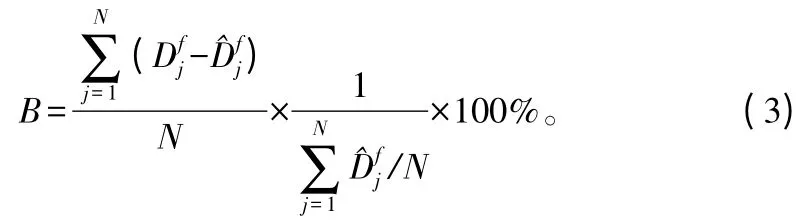
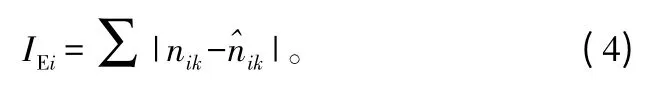
其中:IEi为为第i样地径阶为k的每公顷株数的误差指数;nik和为第i样地径阶为k的每公顷株数的观测值与预测值。

2．4 Weibul分布参数动态预测模型

改进的参数预测模型是将描述林分直径分布的概率密度函数的参数，与林分调查因子(如:林龄、地位指数、优势木高和林分密度等)建立参数预测方程，用林分调查因子预测现实林分的林分结构和收获量［23-24］。林分直径动态预测是利用参数预测技术，建立林分直径结构动态预测模型，用来描述林分直径分布的动态变化规律。首先，利用逐步回归的方法，对前期数据Weibull分布函数的参数b1与一些林分因子进行拟合，发现林分平均直径与b1紧密相关，因此，选用DBH作为变量来构建参数b1的预测模型。参数c1与b1呈显著线性关系。对于复测数据来说，其Weibull分布参数b2与b1有非常好的线关系，c2与b2也有非常好的线性关系［25-27］。由于本研究位置参数a为定值(树木起测直径为5 cm)，因此不对其进行分析。以上几个模型构成了本研究的参数动态预测模型，考虑到模型内的方程间具有内在相关性，本研究采用似乎不相关回归(SUR)理论估计模型的参数［28-29］。参数动态预测模型模型如公式5。

其中:DBH为前期数据林分平均直径;b1、c1为前期数据weibull参数;b2、c2为复测数据weibull参数;α、β、γ以及αi、βi(i=1，2，3)为模型参数。以上模型用SAS/ETS模块的SUR进行拟合［30］。

2．5 模型评价

由于模型的拟合优度不能完全反应模型的预测能力，为了评价模型的预测能力，对模型必须进行检验。因此，本文模型拟合用全部数据，而评价模型预测能力采用“刀切法”［29，31-32］。

2．5．1 参数动态预测模型评价

直径分布参数动态预测模型为多元线性模型，采用以下5个指标对参数动态预测模型进行评价:调整后的确定系数()、均方根误差(RMSE)、平均相对误差(ME)、平均相对误差绝对值(MAE)和预测精度(P)［32-34］。

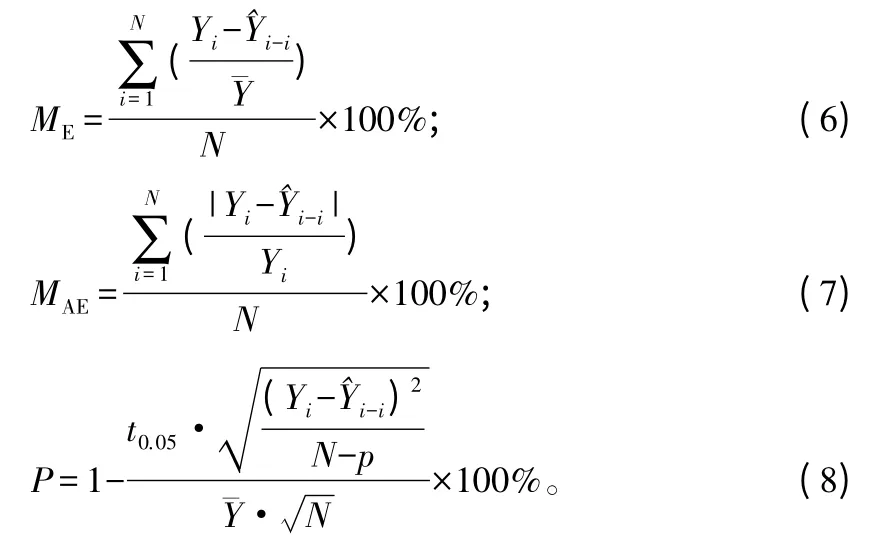
其中:N为样本总数;p为模型的参数个数;Yi是第i个观测值是预测值是观测值的平均值是为原始数据中删除第i个样本观测值后，按p个参数模型拟合回归方程计算Yi的预测值;t0．05为置信水平P=0．05时的t值。

2．5．2 直径分布模型评价

在估计出参数动态预测模型的参数后，需要对其预估能力进行评价，即检验用和反推，得到的直径分布模型的预估能力。在本研究中，其检验指标用公式(3)和公式(4)。需要说明的是，在评价反推直径分布模型预估能力时，需要已知未来林分密度。利用杨锦昌等［21］的株数预估模(n=92，=0．617，RMSE=0．24，P=94．53%)，在已知初始林分密度条件下，建立预测未来林分密度的株数预估模型:

其中，t1、t2分别代表前期和复测的林龄;ISC前期地位级指数，NHt1、NHt2分别代表林龄为t1、t2时的每公顷株数。

3 结果与分析

3．1 直径分布特征

对所有样地直径分布的偏度、峰度进行统计(见表2)。将落叶松人工林样地分成4类:第1类样地为SK＞0且ST＞0，这类林分的林木集中分布在平均胸径处，是工业人工林经营较为理想的林分，但此类实测样地属于立地条件最差、生长较慢、林分分化未开始的林分;第2类样地为SK＞0，ST＜0的林分，这类样地林分激烈分化，被压木生长量甚微，濒临死亡;第3类样地为SK＜0，ST＞0的林分，这类样地林木胸径以平均直径为中心，向两极分化，产生较多的被压木;第4类样地为SK＜0，ST＜0的林分，这类样地为林分结构处于调整初期或是再次调整初期，林分开始分化。总的来说，在这4类落叶松人工林中，第2、3类为需进行抚育间伐林分，此时，间伐既能充分利用林木产品，又能顺应林分结构的自然发育［20］。

由表2可知，对于前期数据而言，102块样地的SK值为-0．468 5～2．805 2，平均值为0．499 0，ST值为-1．212 5～11．737 3，平均值为0．226 9。4类标准地所占比例分别为28．4%、52．9%、1．0%、17．7%，这表明前期数据的直径分布总体上呈右偏的样地占81．3%，曲线顶部较为平坦的样地占70．6%。复测数据的SK值为-0．861 0～2．436 4，平均值为0．242 2，ST值为-1．623 0～8．69，平均值为-0．080 5。4类标准地所占比例分别为24．5%、47．1%、4．9%、23．5%，这表明复测数据的直径分布总体上也呈右偏的样地占71．6%，且曲线顶部较为平坦的样地占70．6%。两期数据对比发现，从前期到复测直径分布总体上呈右偏的趋势有所减少(从81．3%降到71．6%)，但是曲线顶部平坦程度没有改变(均为70．6%)。

表2 落叶松人工林直径分布偏度和峰度统计

由于两期数据204块直径分布都符合Weibull分布，其拟合优度见表3。由表3可知，落叶松人工林Weibull分布函数的误差指数IE较小，前期数据的IE值在320以下，复测数据的IE值为345;每公顷株数相对误差(B0)在2%以内，每公顷直径相对误差(B1)在7%以内，说明用Weibull分布函数拟合两期落叶松人工林直径分布均有着较好的拟合优度。

表3 落叶松人工林Weibull分布拟合优度

3．2 参数动态预测模型拟合及检验

为了预测林分当前和未来时期的直径分布规律，利用符合Weibull分布的102块标准地进行林分直径分布参数动态预测模型的拟合。落叶松人工林参数动态预测模型拟合结果见表4。由表4可知，对于前期数据来说，Weibull分布的尺度参数b1与前期林分平均直径关系紧密相关约为0．9)，Weibull分布函数的形状参数c1与尺度参数b1关系较好，其在0．4以上;对于复测数据来说，Weibull分布的尺度参数b2与b1有着显著的线性关系，其达到了0．5以上，Weibull分布的形状参数c2与尺度参数b2紧密相关，其也达到了0．4以上;所建立的4个参数b1、c1、b2、c2模型的RMSE都较小。总的来看，Weibull分布函数的参数b1与林分平均直径最为密切，复测数据Weibull分布函数的参数与前期数据直径分布参数有着密切的关系，所建立的Weibull分布参数b1、c1、b2、c2预测模型较好，可以对落叶松人工林当前和未来的直径分布进行预估。

我们采用“刀切法”基于公式(6)～(8)及调整后确定系数()和均方根误差(RMSE)评价了落叶松人工林参数动态预测模型。由表4可知，参数b1、c1、b2、c2预测模型的平均相对误差ME为-10%～-2%;绝大多数参数预测模型的平均相对误差绝对值(MAE)在20%以内，只有b2模型的MAE略高于20%，为25．90%;4个参数动态预测模型的预测精度(P)都在95%以上。总的来看，落叶松人工林Weibull分布参数动态预测模型的预估效果较好，可用于研究此地区落叶松人工林直径分布规律。

表4 落叶松人工林参数动态预测模型拟合与检验

此外，我们随机抽取了两块标准样地(23号和85号样地)用来对比其前期数据、复测数据直径分布拟合与预测效果。由图1可以看出，无论是前期数据还是后期数据，拟合分布与预测分布之间相差无几，这更加验证了所建立的参数动态预测方程得出参数b1、c1和b2、c2可以很好的切合两期直径分布。

图1 前期与复测数据直径分布拟合与预测对比分布图

3．3 直径分布检验

图2为两个标准样地(23号和85号样地)前期和复测数据实际分布与预测分布的对比图。由图2可知，两期的直径预测分布与实际直径分布基本吻合。总的来说，本文所建立的动态直径分布模型可为落叶松人工林的合理经营与有效监测等提供基础数据。

表5 落叶松人工林直径分布检验

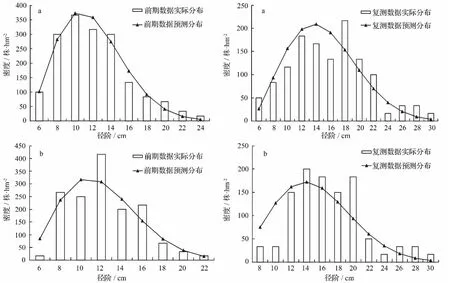
图2 前期与复测数据直径分布拟合与预测直方图

4 结论与讨论

在已知前期林分直径分布的基础上，利用Weibull分布研究了落叶松人工林直径分布的动态规律。在实际应用中，分别建立了前期数据Weibull分布参数b1与前期林分因子之间的关系式以及前期与后期Weibull分布各参数c1与b1，b2与b1，c2与b2之间的线性关系。利用Weibull分布拟合落叶松人工林直径分布参数预测模型时，对Weibull分布参数a不做研究，因为在外业调查中起测直径为5 cm，这导致样地中最小直径定为5 cm。

对所建立的Weibull分布参数预测模型进行了独立性检验。此外，我们也对计算出的Weibull分布参数反推出的直径分布与实际直径分布进行了检验。结果表明:前期与复测数据的Weibull分布参数b、c的预估效果都较好;所建立的4个模型都较高，尺度参数b1与前期林分特征因子的约为0．9，各模型的RMSE都较小。“刀切法”的检验结果显示，参数b1、c1、b2、c2预估模型的平均相对误差ME为-10%～-2%;绝大多数参数预估模型的平均相对误差绝对值在20%以内，所建立的4个参数预测模型的预测精度也都在95%以上。由此可见，Weibull分布参数预测模型具有很好的预估性，能对落叶松人林工直径的动态分布规律进行很好的描述。对于前期与复测数据来说，落叶松人工林的误差指数在525以内，株数相对误差和直径相对误差都较小，分别在5%和13%之内。本研究所建立的直径分布动态预估模型不仅应用了PPM模型，还将后期林分直径分布作为约束条件，实现了动态分布的预测。

林分直径分布是林分结构的基本规律之一，是树种、林龄、林分密度、环境条件及经营措施长期相互作用的结果。而对其动态分布规律进行预估，其目的不仅为了预估下一时期林分各径阶株数和蓄积变化、林木生长量、材种测算，还为建立林分生长、收获预估模型奠定基础，以便科学地指导密度控制技术(如:初植密度选择、抚育间伐等)，最终达到持续地经营森林的目的。总的来说，本文以落叶松人工林为例，建立其Weibull分布参数动态预测模型，为今后直径分布动态预测以及利用其它概率密度函数(如正态分布、负指数分布、SB分布、β分布和Γ分布)建立直径分布动态预测模型提供一定的理论基础。

本研究尚存在的缺陷:第一，在模型变量选择上，变量选择单一。由于利用逐步回归的方法对前期数据Weibull分布函数的参数b1与一些林分因子进行拟合时，发现林分平均直径与b1紧密相关，其余变量(如:林分密度、林龄等)加入模型后都不显著(P＞0．05)。因此，本研究只选用林分平均直径作为变量来构建参数b1预测模型。今后的研究中应加入林龄、林分密度、平均树高等多个林分因子，为今后的实际生产及经营措施提供更多可能的理论依据。第二，没有考虑林木枯损的问题。本研究未建立林木径阶枯损模型并加入到模型系统中，只是建立了简单的林分株数动态预测模型(林分存活木函数)，虽然便于在生产实际中应用，但预测直径结构的精度会有影响，今后的相关研究可以考虑将径阶枯损模型加入到模型系统中。

［1］胡喜生，周新年，兰樟仁，等．人工林桉树胸径分布模型的研究［J］．福建林学院学报，2008，28(4):314-318．

［2］吴承祯，洪伟．林分直径结构新模型研究［J］．西南林学院学报，1999，19(2):90-95．

［3］张伟，赵善伦，吴志芬．山东赤松种群直径结构及其动态研究［J］．西北植物学报，2001，21(4):749-754．

［4］孟宪宇．测树学［M］．3版．北京:中国林业出版社，2006．

［5］Bailey R L，Dell T R．Qualifying diameter distributions with the Weibull function［J］．Forest Science，1973，19(2):97-104．

［6］Clutter JL，Harms W R，Brister G H，et al．Stand structure and yields of site-prepared loblolly Pine plantations in the lower coastal plain of the Carolinas，Georgia，and north Florida［M］．The Forest Servicc，U．S．Department of Agriculture，1984．

［7］Hafley A M，Schreuder H T．Statistical distributions for fitting diameter and height data in even-aged stands［J］．Canadian Journal of Forest Research，1977，7(3):481-487．

［8］Nelson D M．Diameter distribution and growth of loblolly pine［J］．Forest Science，1964，10(1):105-114．

［9］孟宪宇．使用Weibull分布对人工油松林直径分布的研究［J］．北京林学院学报，1985，7(1):30-39．

［10］Bailey R L．Individual tree growth derived from diameter distribution models［J］．Forest Science，1980，26(4):626-632．

［11］Burk T E，Newberry J D．A simple algorithm for moment-based recovery of Weibull distribution parameters［J］．Forest Science，1984，30(2):329-332．

［12］Cao Q V．Predicting parameters of a Weibull function for modeling diameter distribution［J］．Forest Science，2004，50(5):682-685．

［13］Poudel K P，Cao Q V．Evaluation of Methods to Predict Weibull Parameters for Characterizing Diameter Distributions［J］．Forest Science，2013，59(2):243-252．

［14］Ochi N，Cao QV．A comparison of compatible and annual growth models［J］．Forest Science，2003，49(2):285-290．

［15］Qin JH，Cao QV，Blouin D C．Projection of a diameter distribution through time［J］．Canadian Journal of Forest Research，2007，37(1):188-194．

［16］孟宪宇，邱水文．长白落叶松直径分布收获模型的研究［J］．北京林业大学学报，1991，13(4):9-15．

［17］李梦，仲崇淇，李元，等．长白山落叶松人工林直径分布模型的研究［J］．南京林业大学学报，1998，22(1):57-60．

［18］段爱国，张建国，童书振，等．杉木人工林林分直径结构动态变化及其密度效应的研究［J］．林业科学研究，2014，17(2):178-184．

［19］李荣伟，覃志刚，潘攀，等．杜仲人工林林分直径分布研究［J］．四川林业科技，2000，21(2):1-6．

［20］张文勇．思茅松人工幼龄林和中林龄直径分布规律的研究［J］．安徽农业科学，2011，39(13):7736-7737．

［21］杨锦昌，江希钿，许煌灿，等．马尾松人工林直径分布收获模型及其应用研究［J］．林业科学研究，2003，16(5):581-587．

［22］Reynolds M R，Burk T E，Huang W C．Goodness of-fit tests and model selection procedures for diameter distribution models［J］．Forest Science，1988，34(2):373-399．

［23］Maltamo M，Puumalainen J，Paivinen R．Comparison of beta and Weibull functions for modeling basal area diameter distribution in stands of Pinus sylvestris and Picea abies［J］．Scand J For Res，1995，10(1):284-295．

［24］Killkki P，Maltomo M，Mykkänen R，et al．Use of the Weibull function in estimating the basal area dbh-distribution［J］．Silva Fenn，1989，23(4):311-318．

［25］Liu CM，Zhang SY，Lei Y C，et al．Evaluation of three methods for predicting diameter distributions of black spruce(Picea mariana)plantations in central Canada［J］．Can J For Res，2004，34(12):2424-2432．

［26］Newton P F，Lei Y，Zhang SY．A parameter recovery model for estimating black spruce diameter distributions within the context of a stand density management diagram［J］．The Forestry Chronicle，2004，80(3):349-358．

［27］Newton P F，Lei Y，Zhang SY．Stand-level diameter distribution yield model for black spruce plantations［J］．Forest Ecology and Management，2005，209(3):181-192．

［28］Bi H Q，Turner J，Lambert M J．Additive biomass equations for native eucalypt forest trees of temperate Australia［J］．Trees，2004，18(4):467-479．

［29］Li H K，Zhao P X．Improving the accuracy of tree-level aboveground biomass equations with height classification at a large regional scale［J］．Forest Ecology and Management，2013，289:153-163．

［30］SASInstitute Inc．SAS/ETS®9．3．User's Guide［M］．NC:SAS Institute Inc Cary，2011．

［31］Quint T C，Dech J P．Allometric models for predicting the aboveground biomass of Canada yew(Taxuscanadensis Marsh．)from visual and digital cover estimates［J］．Canadian Journal of Forest Research，2010，40(10):2003-2014．

［32］Dong L H，Zhang L J，Li F R．A compatible system of biomass equations for three conifer species in Northeast，China［J］．Forest Ecology and Management，2014，329:306-317．

［33］董利虎，李凤日，贾炜玮，等．含度量误差的黑龙江省主要树种生物量相容性模型［J］．应用生态学报，2011，22(10):2653-2661．

［34］董利虎，李凤日，贾炜玮．林木竞争对红松人工林立木生物量影响及模型研究［J］．北京林业大学学报，2013，35(6):15-22．