基于重复博弈的Ad Hoc网络节点转发策略分析
2015-03-06谭冕何世彪宋波朱国庆张晖
谭冕,何世彪,宋波,朱国庆,张晖
(重庆通信学院,重庆400035)
基于重复博弈的Ad Hoc网络节点转发策略分析
谭冕,何世彪,宋波,朱国庆,张晖
(重庆通信学院,重庆400035)
在无线Ad Hoc网络中,源节点和目的节点互相通信需要中继节点的支持,但节点是理性的,所以可能会拒绝转发请求。这里就节点之间存在的合作问题,对针锋相对策略、冷酷策略、完全合作策略、宽恕的针锋相对策略、严厉针锋相对策略进行了纳什均衡分析。理论分析可知,针锋相对策略相对于其他策略更具优势,因为它的阈值较低。
无线Ad Hoc网络;重复博弈;纳什均衡;转发策略
0 引言
具有无中心、自组织、动态、多跳等特点的无线Ad Hoc网络,由于节点传输距离的有限性,无线Ad Hoc网络需要节点间的合作才能确保数据包得到成功传递[1]。在很多情况下,理性的参与者受到自身存储资源和能量资源等的限制,为了增加存活时间,将采取损害网络性能的行为[2]。显然,即便只存在一些自私节点的无线自组网的系统,也会极大地降低网络的整体性能。
本文首先对系统模型进行了分析,具体包括网络的基本假设、博弈模型假设,再对多种转发策略的纳什均衡和节点收益进行了分析,最后得到了满足纳什均衡的条件。
1 系统模型
1.1 网络基本假设
本文建立的Ad Hoc网络存在如下假设:
(1)网络中存在n个具有理性的节点,网络模型如图1所示。
(2)系统时间是由一系列的协作时隙t构成,在每个时隙,各节点都有数据包发送。
(3)为分析方便起见,特假设任意源节点和目的节点之间都不能直接通信,必须经过中间节点,且到目的节点的跳数基本相同。
(4)所有的数据包大小相等,各节点接收数据包消耗的能量相同,转发数据包消耗同等大小的能量。

图1 网络模型
1.2 博弈模型假设
1.2.1 博弈要素的定义
博弈的三要素是:参与者、策略空间、效用函数。
参与者:分布在当前Ad Hoc网络中理性的节点,都是博弈的参与者,那么它们的集合可以表示为N=(1,2,…,n)。
策略空间:博弈模型中的所有参与者都有一组可供选择的策略集合。在本文中有两种具体策略:合作,转发其他节点的数据包;不合作,不转发其他节点的数据包。
效用函数:即参与者采取某一策略所获得的收益,下述将定义博弈相关参数,并满足囚徒困境博弈的设定。
1.2.2 阶段博弈假设
如图2所示,源节点A和目的节点C无法直接通信,故节点A需要通过中间节点B的转发。

图2 节点转发模型
在博弈中,用c代表节点转发时的能量消耗,用b代表一个节点的数据包被其他节点转发时获得的利益[3]。当博弈双方的策略选择都是合作的时候,效益为(b-c)。如果一个节点在转发数据上采取不合作,而其他节点是合作的话,那么自私节点能够得到b的效益而合作节点的效益为-c。这是因为自私节点的数据包被其他合作节点转发,但是自私节点并没有转发合作节点的数据包。如果双方节点在转发数据上都采取不合作的态度,那么他们的策略收益为(0,0),这是因为节点都没有收益和消耗能量。
基于上述的收益和消耗,建立如表1所示的囚徒困境收益矩阵[4]。

表1 博弈策略收益
无论节点j选择什么策略,对于节点i而言,选择不合作策略是最好的,所以阶段博弈的纳什均衡点是双方节点同时选择不合作策略。然而双方都采取合作策略的收益是最高的,所以在这个收益矩阵中,纳什均衡点并不帕累托占优。原因就在于网络中的节点都是独立和自私的,博弈的双方不知道对方的策略,如果节点i选择了合作,而节点j选择了不合作,那么节点i将会获得最差的收益。所以,自私的节点通常会选择获得最好结果的策略而不冒险获得最差收益[5]。
在囚徒困境的内容设定上,必须满足以下两个条件:

该囚徒困境的收益矩阵如表1所示。
2 重复博弈的纳什均衡和节点收益
由于节点当前行为会对后续的博弈阶段造成影响,所以与邻居节点间的多次交互将不是相互独立的阶段博弈,而形成重复策略博弈[6]。下面研究重复博弈中的重要概念——纳什均衡。
定义1纳什均衡(Nash Equilibrium,NE)[7]策略向量为一个纳什均衡向量,假如对于所有的参与者都有以下式子成立:
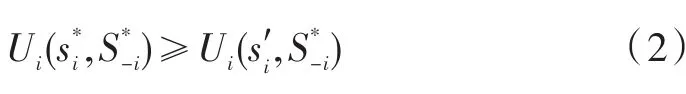
意味着在一个已达到纳什均衡的策略中,没有任何一个理性的参与者能够通过单方面的策略改变而获得收益。如表1的囚徒困境所示,在单次的阶段博弈中,对于参与者M,N而言,双方都选择了不合作策略,尽管是纳什均衡解,但并不是全局最优点,为了让理性的参与者合作,通常有两种办法:博弈的次数为无限次;博弈双方都相信对方不会背叛自己。
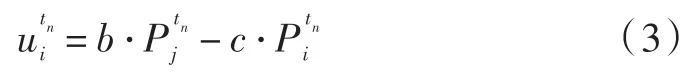
其中,P为某节点阶段博弈采取的策略概率;i和j为博弈的节点;表示的是节点i在第tn个时隙的效用值。
假设重复博弈的时隙总长度为T,节点在各自时隙内的策略都会被观察到。根据重复博弈的原理,节点的收益会在每一个阶段有δ(0<δ<1)的折扣率,它代表节点的历史行为对未来利益的影响,若其值越大则表示节点更加重视一个长期的利益,根据重复博弈论中基于贴现准则的收益评估方式,假设T=∞,用Ui代表节点的平均收益[8],则有:

在博弈中,节点存在的时间有限,若当合作节点都知道其死亡时间,最后一次的博弈必定会选择不合作。当节点都无法预知博弈何时终止时,网络中的节点就必须以无限重复的方式来评估当前策略及其对后来情形的影响。
3 节点转发策略的纳什均衡分析
3.1 针锋相对策略的纳什均衡分析
针锋相对策略[9](Tit-for-Tat,TFT)会根据博弈对手方的策略来制定自己下一步的策略,策略仿佛“回声”般出现。
博弈初始时,所有节点都具有合作意图,能积极转发其他节点的信息,即,其中j为博弈中对方的节点,i为做出行为决策的节点。
TFT策略的概率模型如下:
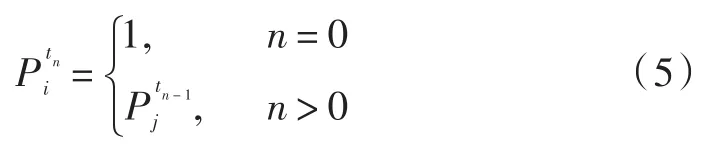
当某个时隙t1,节点i将它的合作概率改为其中0<m<1,则在下一个时隙t2,节点j的合作概率,节点i在t2时隙的合作概率又会变成1,此时两个节点的概率序列如下所示:

在之后的每个博弈阶段,节点i和j都会模仿对方在上一阶段的行为。若节点i采取合作策略,那么节点j也是合作的,如果节点i选择了不合作,那么节点j的策略也是不合作。
将式(6)代入到式(3)和式(4)中可得节点i采取TFT策略的收益为:

又因为节点都是理性的,仅当Ui≥0时才会选择该策略。将其代入式(7)中有:

式(8)即是节点选择TFT策略的纳什均衡条件。
3.2 冷酷策略的纳什均衡分析
冷酷策略[10](Grim Strategy,GS)是一种在博弈中常用的触发策略。初始节点之间都具有合作性,当与节点i博弈的节点j在某个时隙选择了不合作,那么节点i在这个时隙之后的所有策略都将会选择不合作。GS策略将会孤立网络中的自私节点,并且极大地打击存在的自私行为。其概率模型如下:

其中q是节点i的一个触发阈值,当Pi≥q时,这个背叛会被对方节点忽略;当Pi<q,就会令博弈的节点选择永久的不合作策略作为惩戒。如果对方知道你的策略为触发策略,那么对方将不敢采取触发策略,那么博弈双方就可以一直合作下去,即使存在无意的错误,也会被判定为不合作且永远不再合作。本文为方便分析起见,只考虑最差的情况,即Pi<q,故概率序列如下:

将式(10)代入到式(3)和式(4)中可得节点i采取GS策略的收益为:

又因为节点都是理性的,仅当Ui≥0时才会选择该策略。将其代入式(11)中有:

式(12)即是节点选择GS策略的纳什均衡条件。
3.3 完全合作策略的纳什均衡分析
完全合作策略(Full Cooperation Strategy,FCS)基于理想的情况之下,所有节点在博弈的任意阶段都会选择合作策略,在本文中作为一种对比策略引入。其概率序列如下:

将式(13)代入到式(3)和式(4)中可得节点i采取完全合作策略的收益为:
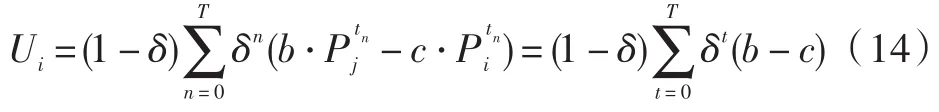
又因为节点都是理性的,仅当Ui≥0时才会选择该策略。将其代入式(14)中有:

式(15)即是节点选择FCS策略的纳什均衡条件。
3.4 宽恕的针锋相对策略的纳什均衡分析
宽恕的针锋相对策略(Tit-for-Tat with Forgiveness,TFTF)是在经历对方的一个不合作行为后,节点以一个小概率m()
0<m<1去选择合作,并如同TFT策略一般交替出现。
为方便讨论起见,假设其概率序列如下:

将式(16)代入到式(3)和式(4)中可得节点i采取完全合作策略的收益为:

又因为节点都是理性的,仅当Ui≥0时才会选择该策略。将其代入式(17)中有:

3.5 严厉针锋相对策略的纳什均衡分析
严厉针锋相对策略(Stern Tit-for-Tat,STFT)[11]是指当节点出现不合作行为时,其所有邻居节点对它执行若干时隙的拒绝合作的惩罚,且其本身策略为合作。惩罚期间结束后邻居节点选择遗忘对方的不合作行为,重新开始合作。
为方便分析起见,令惩罚期为3个时隙,且重新合作后又出现不合作行为,设定其概率序列如下:

将式(20)代入到式(3)和式(4)中可得节点i采取完全合作策略的收益为:
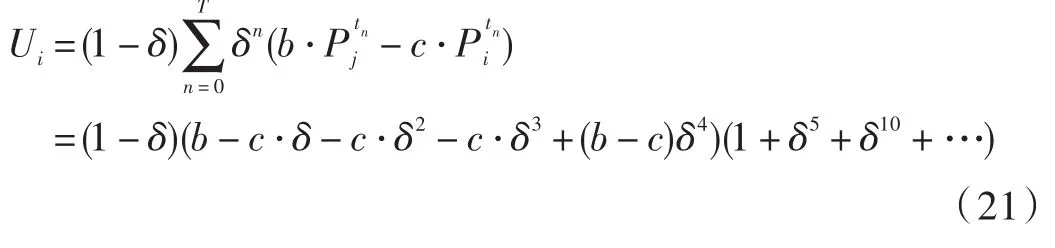
又因为节点都是理性的,仅当Ui≥0时才会选择该策略。将其代入式(21)中有:
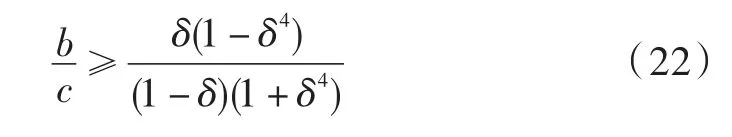
4 结语
无线Ad Hoc网络起源于军事运用,时至今日已得到广泛的关注,由于其分布式的特点,导致每个节点都会对网络造成影响,故促进节点之间的合作是有必要的。本文对TFT策略、GS策略、FCS策略、TFTF策略、STFT策略进行了满足纳什均衡的条件比较[12-13],通过对比可以得知TFT策略更易满足该条件。
[1]KHALILI A,BAZZI W M,RASTEGARNIA A.Cooperation gain in incremental LMS adaptive networks with noisy links [C]//Proceedings of 2012 SPIT Second International Conference.Dubai:SPIT,2012:107-114.
[2]RAMACHANDRAN S,SHANMUGAM V.Performance comparison of routing attacks in manet and WSN[J].International Journal of Ad Hoc,Sensor&Ubiquitous Computing,2012,3(4):361-369.
[3]BADE S,KUMAR M,KAMAT P.A reactive energy-alert algorithm for MANET and its impact on node energy consumption [J].International Journal of Computer Applications,2013,71(18):267-272.
[4]JIN Q,WANG Z,WANG Y L.Strategy changing penalty promotes cooperation in spatial prisoner′s dilemma game[J].Chaos,Solitons&Fractals,2012,45(4):395-401.
[5]ROCA C P,SANCHEZ A,CUESTA J A.Individual strategy update and emergence of cooperation in social networks[J]. The Journal of Mathematical Sociology,2012,36(1):1-21.
[6]LEI T,XIANG M S.Research of avoid the selfish behavior in mobile Ad Hoc networks based on repeated game[C]//Proceedings of 2012 the Fourth IEEE International Conference on Multimedia Information Networking and Security.Nanjing,China:IEEE,2012:835-838.
[7]WANG Y,XU Q,LIU Z.Fair computation with tit-for-tat strategy[C]//Proceedings of 2013 the 5th IEEE International Conference on Intelligent Networking and Collaborative Systems.[S. l.]:IEEE,2013:309-314.
[8]SRIVASTAVA V,DASILVA L A.Equilibria for node participation in Ad Hoc networks-an imperfect monitoring approach [C]//Proceedings of 2006 IEEE International Conference on Communications.Istanbul:IEEE,2006,8:3850-3855.
[9]BOYER S,ROBERT J M,ROUSSEAU C,et al.A novel reputation-based tit-for-tat strategy for IEEE 802.11 CSMA/CA protocol[C]//Proceedings of 2012 IEEE Consumer Communications and Networking Conference.Las Vegas:IEEE,2012:143-148.
[10]WANG J,CAI Y Q.A rational secret sharing scheme based on repeated game[C]//Proceedings of 2011 the 7th IEEE International Conference on Computational Intelligence and Security.Hainan,China:IEEE,2011:615-619.
[11]闻英友,赵博,赵宏.基于博弈理论的移动自组网激励机制研究[J].通信学报,2014,35(4):44-52.
[12]徐许亮,董荣胜,刘亮龙.无线自组网中节点协作的纳什均衡研究[J].计算机工程,2010,36(4):107-109.
[13]孙玉星,赵燕飞,李娅,等.基于概率博弈的无线自组网信任推荐激励策略的研究[J].计算机科学,2011,38(4):65-71.
Analysis for forwarding strategy of Ad Hoc network node based on repeated game
TAN Mian,HE Shibiao,SONG Bo,ZHU Guoqing,ZHANG Hui
(Chongqing Communication Institute,Chongqing 400035,China)
In wireless Ad Hoc network,the intercommunication between the source and destination nodes needs the support of relay node.Since the node is rational,it may refuse the forwarding requests.For the cooperation problem among the nodes,the tit-for-tat strategy,grim strategy,full cooperation strategy,tolerant tit-for-tat strategy and severe tit-for-tat strategy are analyzed with Nash equilibrium.According to the theoretical analysis,the tit-for-tat strategy is more advantageous than other strategies because of its low threshold value.
wireless Ad Hoc network;repeated game;Nash equilibrium;forwarding strategy
TN92-34
A
1004-373X(2015)23-0020-04
10.16652/j.issn.1004-373x.2015.23.006
谭冕(1989—),男,重庆人,硕士研究生。主要研究方向为抗干扰通信、无线Ad Hoc网络的节点合作研究。
2015-04-04
重庆市自然科学基金资助项目(cstc2014jcyjA40051)
