“4·20”地震后芦山县灾害应急支援响应分析
2015-03-06丁明涛
庙 成,丁明涛
(西南科技大学环境与资源学院,四川绵阳 621010)
0 引言
21世纪以来,全球多次出现较大规模的灾害。为了在灾后尽可能多的挽救受灾区人民的生命和财产损失,需要受灾区以外地区的及时应急支援响应。
随着全球灾害的频发和科学技术的发展,使得灾害应急响应向多学科融合和多地区合作的趋势发展。1987年12月11日联合国决定:“从1990年开始到20世纪的最后十年定名为‘国际减轻自然灾害十年(IDNDR)’。在这十年内,各国际团体要在联合国的主持下特别关注和扶植在减轻自然灾害领域中的国际合作”[1]。在这样的环境下,我国灾害应急响应研究工作全面的展开。翟晓敏等在总结灾害特征以及对人类社会危害的基础上,概述当今应急响应研究的现状、水平和趋势及不足,提出今后应急研究的重点[2];单修政、徐世芳根据地震灾害的特点和成灾规律,对目前国内外紧急救援工作中的组织结构、人力物力及专业技术问题进行了综合论述[3];陈红旗,徐永强,庄茂国等探讨了地质灾害应急支撑体系建设的基本问题[4];唐川通过城市突发性地质灾害管理进展分析,将灾害应急分成多个不同的系统,使灾害应急响应更加的整体化,为制定减灾预案提供方便的服务[5]。学者们在对整体的灾害应急响应认识总结后,开始将工作深入化。对灾害响应评价指标体系[6]、灾害响应评价方法[7]、灾害响应能力的综合评价[8]等方面全面深入的研究。随着研究深入,一些学者通过对国外灾害应急响应减灾措施[9]的学习与借鉴,建立一定的算法来解决灾害响应中减灾救灾措施方法的优化等问题,通过算法的设计,讨论多应急资源的优化配置问题,效果显著[10]。综上通过对灾害响应的研究来分析,我国学者主要将研究的重点放在了对灾害应急响应的综合研究和具体的量化评价上,对于产生灾害地区的邻近区域给予的灾害应急支援响应区划研究较少。
本文以“4.20”雅安地震芦山县邻近17个县(市、区)为研究对象,采用主成分聚类分析法讨论这些地区在雅安地震后给予震中芦山县的应急支援响应能力情况,并对其进行区划,为震后芦山县的灾害救援提供相应的决策依据。
1 概况
四川省芦山县位于四川盆地西部,雅安地区东北部,青衣江上游,地理坐标为东经 102°52'~103°11',北纬30°01'~30°49'(图 1)。区域内以山地为主,地形起伏和河流比降较大。同时研究区处于龙门山北东向构造带上,受宝兴地震带和石棉地震带影响明显。气候为亚热带湿润季风气候,雨量充沛,降雨集中。区内交通便利,少数民族众多,历史遗存丰富,人文景观独特,但生产生活条件差,人口增长过快,经济相对落后。
2013年4月20日8时02分四川省雅安市芦山县发生Ms7.0级强烈地震,震源深度13 km,震中距成都约100 km。据雅安市政府应急办通报,震中芦山县龙门乡99% 以上房屋垮塌,卫生院、住院部停止工作,停水停电。雅安地震的发生对当地人们生命财产安全产生很大的威胁,特别是震中芦山县,损失较为严重。

图1 研究区位置图Fig.1 Location map of the study area
2 研究方法
主成分聚类分析法是主成分分析法和聚类分析法两者的结合。在实际问题中,主成分聚类分析法是先通过主成分分析,将实际问题中的指标进行降维,把多个指标综合成少数主成分指标,再利用聚类分析对主成分指标进行聚类,最后再将聚类结果与主成分分析得分的排序结果综合起来,对研究对象进行分析。这样做即可将多个指标综合后由少数几个保留了原始信息但彼此之间无关联的主成分代替,又提升了原始指标的优越性,更容易探寻到事物的本质规律,同时又进一步加强了对于实际问题的定量化表达。主成分聚类分析法的具体过程步骤如下[11]:
(1)原始数据标准化处理
由于具体实例所选的指标因子不同,指标的量纲、数量级和数量变化幅度存在差异,这些差异可能对最终分析结果产生影响,同时指标之间也会有不小的影响,为了消除这些影响,故首先要对数据统一进行消除量纲的处理,即标准化处理。本文根据需要选择了标准差标准化的方法。
原始数据:
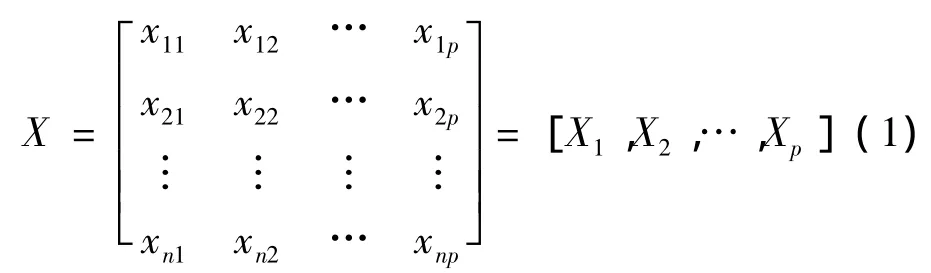
标准差标准化即:
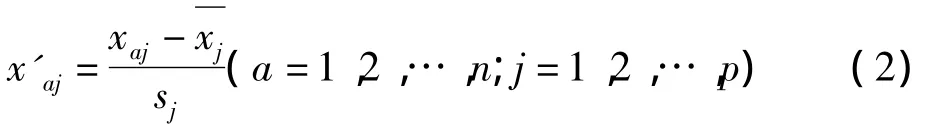
其中:

经过标准化后原始矩阵X转化成矩阵X':
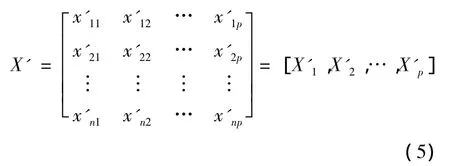
(2)计算相关系数矩阵
对得到的新矩阵X'进行相关系数的计算:
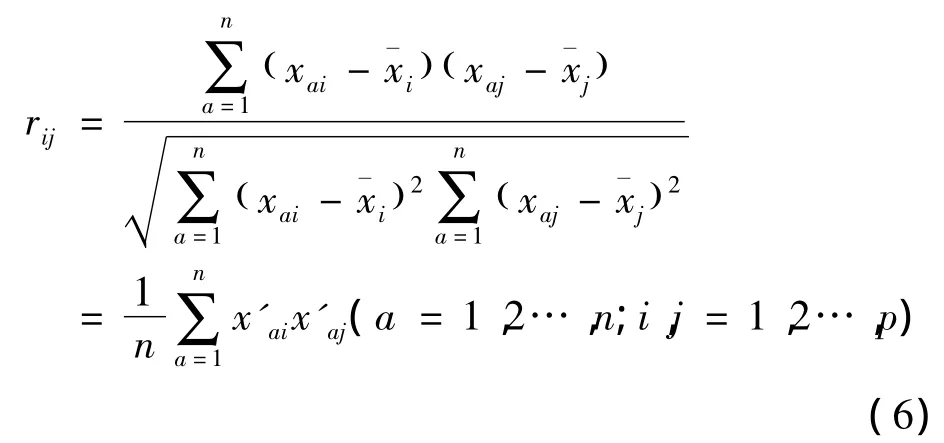
其中rij是指标xi与xj之间的相关系数。经过运算后的得到相关系数矩阵R:

(3)计算特征值和特征向量
对相关系数矩阵R进行特征值和特征向量的计算。根据特征方程∣R-λI∣=0计算特征值,并使其按大小顺序排列,即 λ1≥λ2≥,…,≥λp≥0;然后分别求出特征值λi(i=1,2,…,p)对应的特征向量ei=[ei1,ei2,…eip]T(i=1,2,…,p)。
(4)计算贡献率和累计贡献率,确定主成分个数
进行主成分贡献率和累计主成分贡献率的计算,当累计贡献率达85% ~95%[11-12],即取当前的m个特征值所对应的为m个主成分(m≤p)。其中累计贡献率为:
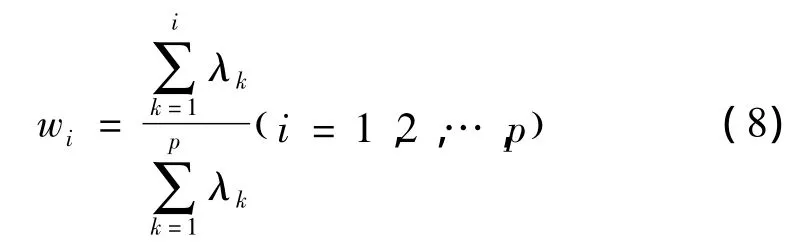
(5)计算主成分得分
计算样本的主成分上的得分。首先需要计算各主成分的荷载:
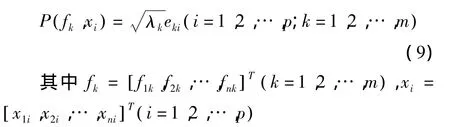
经过计算后得到各主成分的荷载以后,再利用公式计算主成分得分:
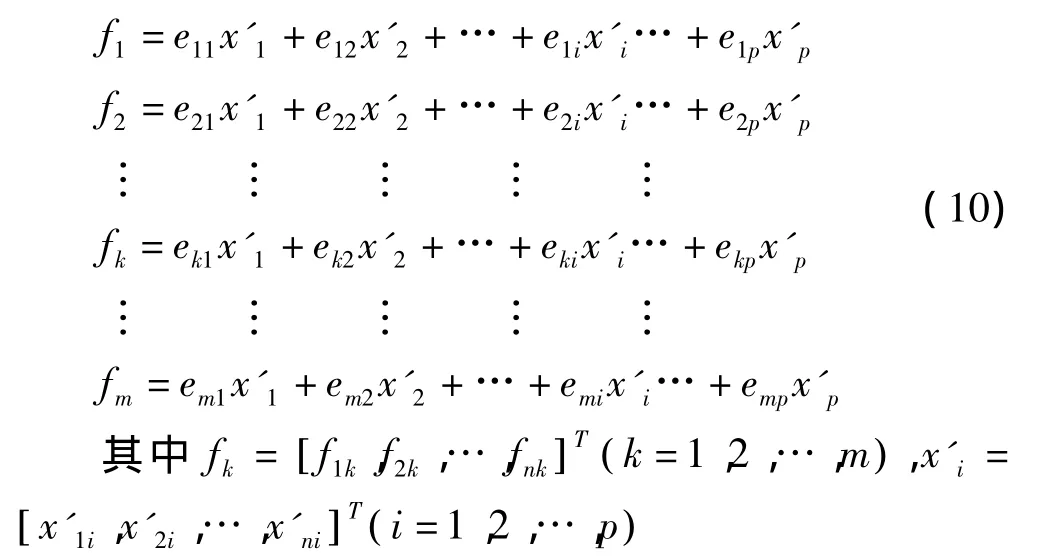
经过计算后得到主成分得分矩阵:
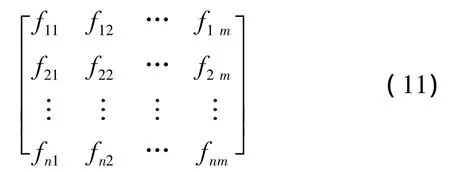
在运用公式计算总得分F,为综合分析做准备:
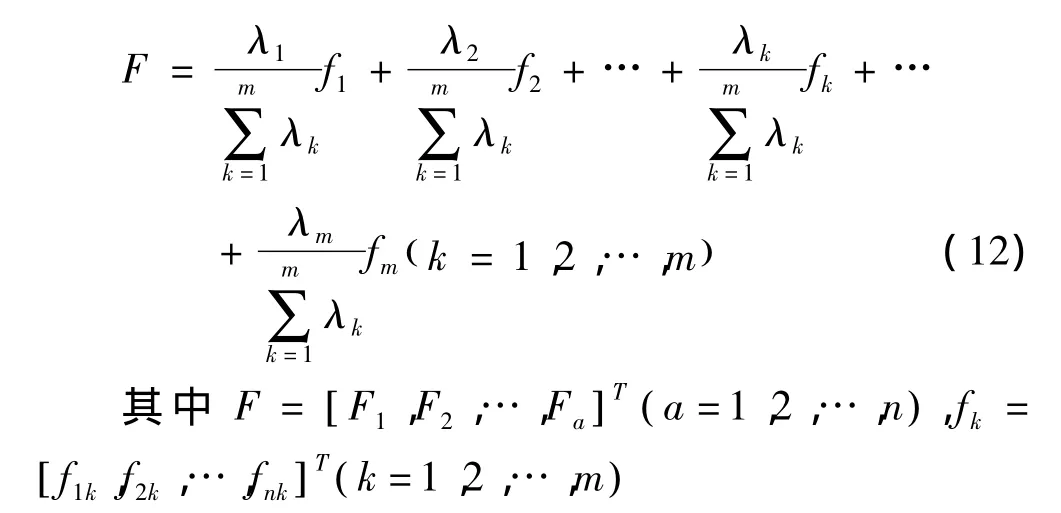
式中:F——代表样本总得分;
fk——代表第k主成分得分;
λk——代表第k主成分对应特征值。
(6)计算距离系数,进行样本归类
利用主成分分析得到的得分矩阵,计算距离系数。距离系数的计算有多种方法,本文选择欧氏距离进行计算。
欧氏距离即:
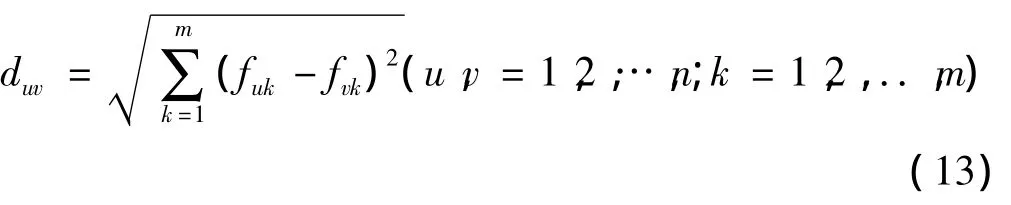
式中:u和v——代表样本;
k——代表第k个主成分;
fuk——代表第u样本的第k个主成分的值;
fvk——代表第v样本的第k个主成分的值。
计算得出的欧氏距离矩阵采用系统聚类分析法进行样本聚类,处理后得到聚类谱系图。
(7)结果分析
利用主成分得分矩阵和聚类结果谱系图,对样本进行分类分级,并对最终所得结果进行讨论。
3 案例应用
3.1 数据来源
(1)中国国家地震局(http://www.cea.gov.cn/)提供的芦山地震相关信息及数据;
(2)四川省统计局和国家统计局四川调查总队共同主编由中国统计出版社出版的《四川省统计年鉴》;
(3)国家科技基础条件平台——地球系统科学数据共享平台(四川芦山地震救灾专题数据库http://www.geodata.cn/extra/TopicsWin/?isCookie Checked=true.)提供的社会经济统计数据等基础数据资料。
3.2 分析对象选择
根据“4.20”地震后芦山县的受灾情况分析,得到芦山县需要其他区域给予及时的应急支援响应。在遵循尽可能多的挽救受灾区生命和减少受灾区财产损失的要求下,同时对区位条件在救灾中所占优势的考虑,选择芦山县邻近17个县(市、区)。
3.3 灾害支援响应指标
根据对美国联邦政府灾害响应计划中关于灾害响应指标的研究[12]和我国学者对于灾害应急能力评价指标体系的研究[6-8]的分析,以及对“4·20”地震后芦山县的实际资料和芦山县邻近县(市、区)基础资料的解析,在以把握地震发生后的72 h(“黄金救援时间”)为准则和遵循系统性、科学性、全面性、可操作性的原则下,选取具有代表性的指标:交通(公路里程(X1)、公路货物周转量(X2)、公路旅客周转量(X3))、医疗(卫生院卫生技术人员数(X4)、医院、卫生院床位数(X5))、人员素质(总人口数(X6)、受教育程度——初中以上学历人口数(X7))、区域经济实力(GDP(X8))、紧急安置场所(学校数、福利院数(综合为一个指标)(X9))、物资(地区的粮食产量(X10))6个方面中的10个指标因子,对研究区进行应急支援响应能力的分析。
3.4 应急支援响应的主成分聚类分析结果
(1)根据芦山县邻近17个县(市、区)10个指标因子的原始数据,利用SPSS19.0软件进行标准差标准化处理,消除指标之间量纲的影响,得到标准化后数据,然后进行主成分分析,可得到指标之间的相关系数矩阵R以及相关系数的特征值、贡献率、累计贡献率(表1)、主成分荷载矩阵。一般按照主成分分析法中特征值≥1(或近于1)和累计贡献率85% ~95%的要求[11],最终确定主成分中前2个成分符合要求(成分1和2特征值分别为6.729、1.842,累计贡献率为85.718%),可用来综合代替原始的10个指标因子,分析17个县市的应急支援响应能力(表1)。
(2)在芦山县邻近17个县(市、区)相关系数的特征值、贡献率、累计贡献率(表1)的基础上,结合芦山县邻近17个县(市、区)的主成分荷载矩阵,分析可以得到第一主成分的方差贡献率达67.294%,是对芦山县邻近17个县(市、区)应急支援响应能力的主要影响因素。第一主成分在 X1、X4、X5、X6、X7、X8、X9、X10上荷载较大,综合反映出某些地区在医疗、人员素质、区域经济实力、紧急安置场所、物资条件上是占有优势的,体现这些地区易于给予受灾区人员、物资等方面上持续的帮助。第二主成分在X2、X3上荷载较大,说明某些地区的交通条件是优势指标,反应这些地区易于快速的集结反应和调用人员物资。将这两个主成分综合起来,可以很好的反应芦山县邻近17个县市的灾害应急支援响应情况(表1)。
(3)通过运用上述的主成分得分计算公式,计算出芦山县邻近17个县(市、区)的第一、二主成分的得分以及综合得分,并对结果进行排序(表2)。
(4)利用系统聚类法,在SPSS19.0软件中对主成分分析后的数据进行聚类,得到芦山县邻近17个县(市、区)聚类结果谱系图(图2)。
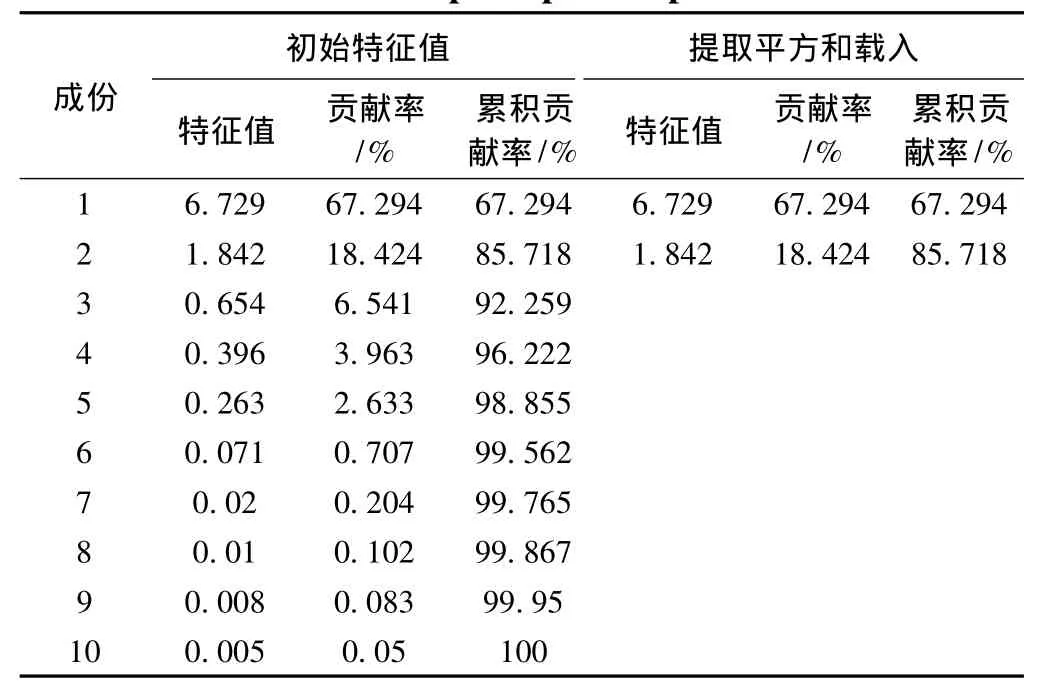
表1 芦山县邻近17个县(市、区)相关系数的特征值、贡献率、累计贡献率Table 1 Eigenvalues,contribution rate and accumulative contribution rate of principal component variance
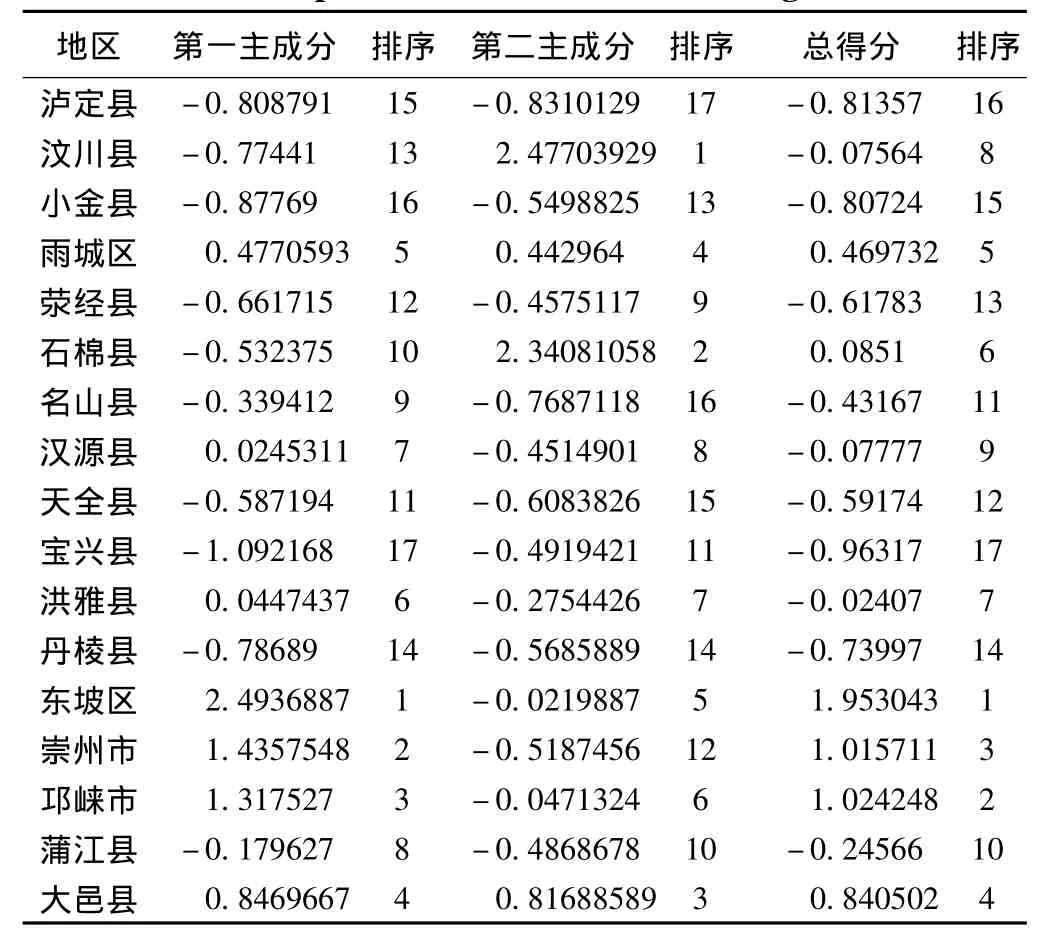
表2 芦山县邻近17个县市主成分得分及其排序Table 2 The first two principal component scores,comprehensive scores and ranking
3.5 主成分聚类结果分析
(1)东坡区、崇州市、邛崃市三个城市的综合得分排在前三位,其聚类结果为一类,代表这三个地区给予芦山县的应急支援处在一个较高的水平。同时由于这三个城市的第一主成分得分处在前3位,说明三个城市主要对于芦山县是在医疗、人员、场地以及物资方面的支持,而且比较具有持续性的优势。但是,根据第二主成分的得分情况看,这三个城市在交通方面的响应能力并不是很明显。因此,三个城市在实际中给予芦山县应急响应支持时,需要酌情考虑交通方面对于其他方面指标的影响。
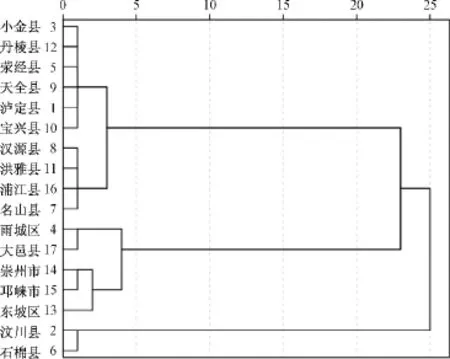
图2 芦山县邻近地区灾害应急支援响应聚类结果谱系图Fig.2 Cluster dendrite diagrams of the first two principal components
(2)大邑县、雨城区主成分综合得分处在整体的第4和5位,聚类分析后将其归为一类。两城市的灾害应急支援响应能力处在研究区域的第二梯度,在第一主成分和第二主成分上实力均衡,说明在交通、医疗、人员、场所、物资方面上,两城市的灾害支援响应能力是具有即时和持续性的特点,可以给予受灾区较为稳定的支持。
(3)汶川县、石棉县综合得分分别处于第6位和第8位,聚类分析将其归为一类,整体灾害应急支援响应能力处于第三等级上,主要在于汶川县和石棉县两个城市的第二主成分得分排在整体的前两位,体现两个城市在给予芦山县应急支援响应的交通指标方面优势较为明显,两个城市在实际救灾时因具有良好的交通条件,可以很快的聚集大量的人员和物资,给予受灾区以支持,但在其他方面,两个城市的支援能力较弱,并不能给予受灾区以持续性的支持。
(4)汉源县、洪雅县、浦江县、名山县的整体灾害应急支援响应实力处在第四级上,聚类分析后将4个城市归为一类,从主成分得分上分析,这4个城市的得分情况较为接近,处在整体中部偏下的水平上,对芦山县给予的支援响应,可以作为其他具有优势支援能力城市的候补地区或者是作为优先支援城市人员、物资、场所的后备区。
(5)小金县、丹棱县、荥经县、天全县、泸定县、宝兴县6个县的主成分总得分和第一、二主成分得分均处在整个研究区得分排序的最后,聚类分析后将其归为一类,说明这6个县给予芦山县的灾害应急支援响应能力最低,只有个别的县在某一方面具有相对较高的优势。综合考虑,这6个县在灾后应当给具有支援优势的县市区让开救援通道,给这些地区以政策上的支持以及转移优势指标到具有优先支援的地区,为尽可能多的挽救受灾区生命和减少财产损失做贡献。
4 结论
(1)“4.20”雅安地震芦山县邻近17个县(市、区)的灾害应急支援响应与交通、医疗、人员素质、区域经济实力、紧急安置场所、物资6个方面中的10个指标因子关联程度较好,经主成分聚类分析后结果分类分级明显,对应急支援响应具有良好的决策指导意义。
(2)经主成分聚类分析后,将芦山县邻近17个县(市、区)灾害应急支援响应能力划归为5类,同时划分为五级(从高到低):东坡区、崇州市、邛崃市为1类(一级支援响应区);大邑县、雨城区为2类(二级支援响应区);汶川县、石棉县为3类(三级支援响应区);汉源县、洪雅县、浦江县、名山县为4类(四级支援响应区);小金县、丹棱县、荥经县、天全县、泸定县、宝兴县为5类(五级支援响应区)。这五个区域的分级归类是与相应的指标有着密切的关系,支援的指标不同造成每个区域给予芦山县的灾害应急支援响应程度也是不一样的。
(3)本文对于“4.20”地震后灾害应急能力的研究,只是从灾害应急支援响应能力方面进行了考虑,关于受灾区自身的响应程度,救援情况以及灾害造成的损失评价等很多方面没有涉及,需要在今后的工作中进行深入的研究,使这些逐渐形成一个体系,为今后的灾害应急响应能够提供一定的理论和实践指导。
[1]国家地震局震害防御司,自然灾害学报编辑部(编译).国际减轻自然灾害十年计划的实施[M].北京:地震出版社,1990.China earthquake administration,Journal of natural disasters.International decade for natural disaster reduction[M].Beijing:Seismological Press,1990.
[2]翟晓敏,盛昭瀚,何建敏.应急研究综述与展望[J].系统工程理论与实践,1998(7):17-24.ZHAIXiaomin, SHENG Zhaohan, HE Jianmin.Recent development of emergency study[J].Systems Engineering-theory and Practice,1998(7):17-24.
[3]单修政,徐世芳.地震灾害紧急救援问题综述[J].灾害学,2002,17(3):71-75.SHAN Xiuzheng,XU Shifang. An overview of earthquake disaster emergency relief[J].Journal of Catastrophology,2002,17(3):71-75.
[4]陈红旗,徐永强,庄茂国,等.地质灾害应急支撑体系建设基本问题分析[J].中国地质灾害与防治学报,2011,22(4):108-111.CHEN Hongqi,XU Yongqiang,ZHUANG Maoguo,et al.Study on the construction of geological disaster emergency support system [J].The Chinese Journal of Geological Hazard and Control,2011,22(4):108-111.
[5]唐川.城市突发性地质灾害应急系统探讨[J].中国地质灾害与防治学报,2005,16(3):104-110.TANG Chuan.Approaches on emergency response system of abrupt geological hazard associated with urban areas[J].The Chinese Journal of Geological Hazard and Control,2005,16(3):104-110.
[6]迟娜娜.城市灾害应急能力评价指标体系研究[D].北京:首都经济贸易大学,2006.CHI Nana.Assessment indexes of city emergency planning institute[D].Beijing:Capital University of Economics and Business,2006.
[7]黄炎焱.面向突发灾害事件的应急效能评估方法[J].自然灾害学报,2012,21(1):71-77.HUANG Yanyan.Abrupt disaster events oriented emergency response effectiveness evaluation method[J].Journal of Natural Disaster,2012,21(1):71-77.
[8]唐桂娟.城市自然灾害应急能力综合评价研究[D].哈尔滨:哈尔滨工业大学,2011.TANG Guijuan.Research on integrated evaluation of urban natural disaster emergency capability[D].Harbin:Harbin Institute of Technology,2011.
[9]Carmen G. Rawls, Mark A. Turnquist. Prepositioning of emergency supplies for disaster response[J].Transportation Research Part B,2010,(44):521-534.
[10]ZHANG Jianghua,LI Jin,LIU Zhiping.Multipleresource and multiple-depot emergency response problem considering secondary disasters[J].Expert Systems with Applications,2012,(39):66-71.
[11]张超,杨秉赓.计量地理学(第二版)[M].北京:高等教育出版社,1991.ZHANG Chao,YANG Binggeng.The measurement geographyfoundation (Second Edition) [M].Beijing:Higher Education Press,1991.
[12]黄宏.美国联邦政府灾害响应计划[J].全球科技经济瞭望,1999(1):46-47.HUANG Hong.America federal disaster response plan[J].GlobalScience Technology and Economy Outlook,1999(1):46-47.
