一种简化的区间B样条小波杂交应力元

卿光辉，张春潮

（中国民航大学航空工程学院，天津 300300）

一种简化的区间B样条小波杂交应力元

卿光辉，张春潮

（中国民航大学航空工程学院，天津 300300）

结合杂交应力元理论，分别以2阶、4阶0尺度小波函数为基础，构造了一种对应于杂交应力元的简单形函数。这种形函数不仅克服了区间网格数成2的指数级增加而导致未知量增加的困难，同时简化了计算过程。为了验证理论的正确性，分析了二维弹性板在承受均布载荷下中线位移和应力的情况。在相同网格数的情况下，4阶小波尺度函数构造的杂交应力元计算结果比2阶的计算结果更加准确。

有限元；杂交应力元；小波函数；形函数

小波有限元继承了传统有限元法离散逼近的优点，能有效处理复杂的边界条件[1]。同时，由于小波函数拥有多分辨、多尺度特性，所以得到一种提高精度的细化算法，即小波有限元在不改变网格划分的条件下提高其分辨率，使其可以在问题大梯度处、小梯度处分别采用高阶单元和低阶单元，从而提高分析精度和分析效率[2]。

杂交单元应力场和应变场都是独立假设的，所以可作为独立的变量来求解，而不像位移法那样求解单元的应力依赖于求解位移的导数。因此，基于杂交单元方法，不但应力精度更高，而且还具有数值稳定性好的优点[3]。传统位移法等参元所遇到解的自锁问题对杂交单元来说是不存在的，或容易解决。杂交单元灵活地构造和选配单元应力场，对于确保裂纹前沿等奇异性问题和复合材料界面问题的可靠性非常重要[4]。

由于小波函数在数学计算上的复杂性，目前只在科研和工程上广泛应用，但可以预见，随着研究的不断深入，小波杂交元将会成为有限元一个强有力的分支，未来有可能具有与普通的位移元方法一样广泛的工程应用前景。

文献[5]中采用小波单元时，在区域内以n×n（n= 2j+m-2，j＞jO，jO为保证至少有一个内部小波的最小尺度）的形式划分网格，这样的网格划分具有一定的局限性。特别是所用的样条小波函数的阶数较大时，网格将会成2的指数级增加，毫无疑问，对于一般的问题，这样处理会给数值计算带来困难。

本文在不影响计算结果精度的情况下，对小波插值函数进行了简化。即通过直接使用某一区间段上的样条小波尺度函数，结合杂交应力元理论的推导方法，按照形函数的性质构造了一种简单的形函数。这种处理方法克服了网格数成2的指数级增加而导致未知量增加的困难，并使得计算更加方便、快捷。

1 杂交应力元

首先，在单元内部假设独立的应力场

其中：P={σ1…σM}为应力矩阵；σi为假设的应力模式；βi为对应的应力参数。位移场

根据（H-R）广义变分原理[6]，可获得应力参数和节点位移之间的关系为

因此，矩阵形式的控制方程为

其中

为单元刚度矩阵；fe为等效节点载荷；G为杠杆矩阵；H为单元柔度矩阵，其相应的表达式为

其中

为柔度矩阵；E为弹性模量；μ为泊松比。

根据一般有限元的方法，可以求得未知节点位移ae。然后由式（2）求得单元位移场，并由式（1）和式（3）求得单元应力场[6]为

2 小波单元的构造

以下由B样条小波函数的尺度函数构造满足形函数条件的小波插值函数，并在此基础上构造出求解平面问题的小波杂交应力单元。

2.1 插值函数的选择

0尺度2阶和4阶样条小波尺度函数的表达式分别如下[2]

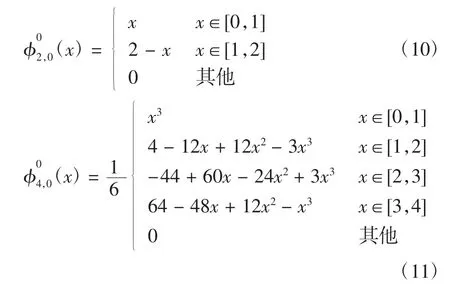
2.2 二维四节点2阶样条小波单元

自然坐标系中二维四节点单元如图1所示。

图1 自然坐标系中二维四节点单元Fig.1 2-D four-node element of natural coordinates

在文献[6-7]中，是以矩阵的形式假设位移模式。但在这里，采用以下形式假设单元中任一点的横向位移模式[8]为

其中，a1、a2、a3、a4为待定系数。当ξ=-1，η=-1时，u= u1=a4；当ξ=1，η=-1时，u=u2=a2；当ξ=1，η=1时，u=u3=a1；当ξ=-1，η=1时，u=u4=a3。

于是可得

因此，式（12）可写成

同理可得单元内任一点纵向位移v，其形式与式（12）相同。因此，小波形函数为

将式（13）代入式（2），可求得二维四节点小波单元的位移场

其中：ue为单元位移场

为单元节点位移列阵

为小波插值函数。

2.3 二维四节点4阶样条小波单元

采用与2阶样条小波相似的方法，假设单元中任一点的横向位移为

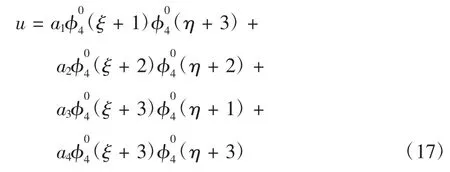
同理，可以求出式（17）中的系数

所以可得到其形函数为

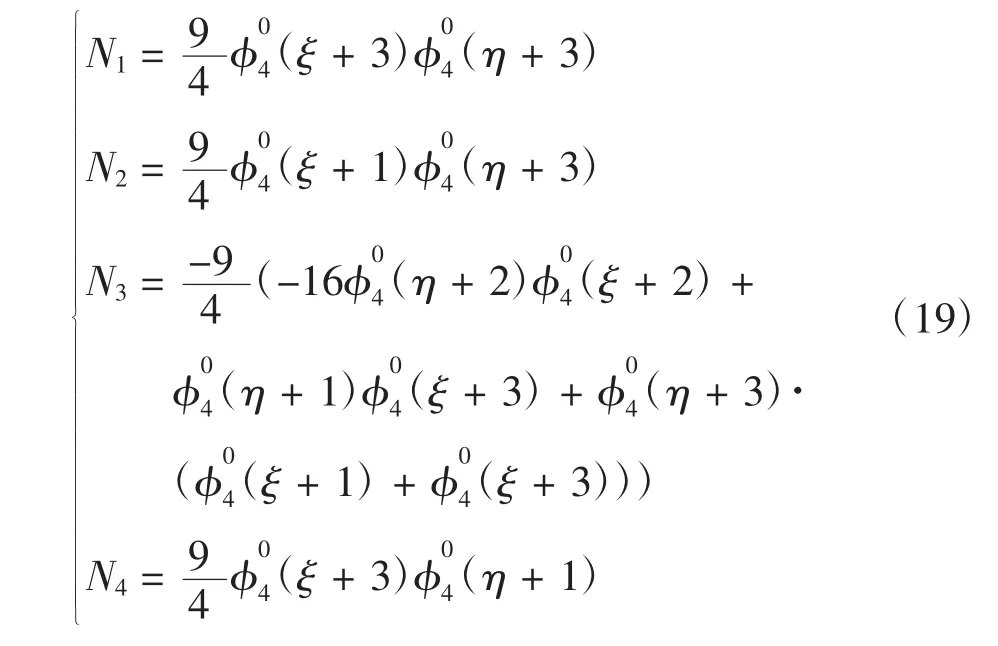
3 应用实例

算例1 如图2和图3所示，二维空间中有一两端固支正方形弹性平面体，厚度t=0.1 m，长度L=1 m，弹性模量E=3×104Pa（本文的弹性模量与参考文献相比做了变化，但只会影响位移的数量级，计算误差时没有影响，即E的阶数变小使变形图的变形更明显），泊松比μ=0.16，在其面内承受y方向的均布载荷q=1×105N/m[2]。

图2 承受面内均布载荷作用的两边固支板（30×30）Fig.2 Both sides of fixed plate under uniformly distributed loads（30×30）

在以下的数值对比中，取模型中有代表性的点进行比较分析，即取中线（沿x方向）上节点的位移v与中线（沿y方向）上节点的应力σx与对应的理论解[9]比较，同时用ANSYS软件分别建立30×30和20×20网格有限元模型分析计算。最后分别计算误差，如表1和表2所示。其变形图如4所示。

图4 网格划分Fig.4 Grid division

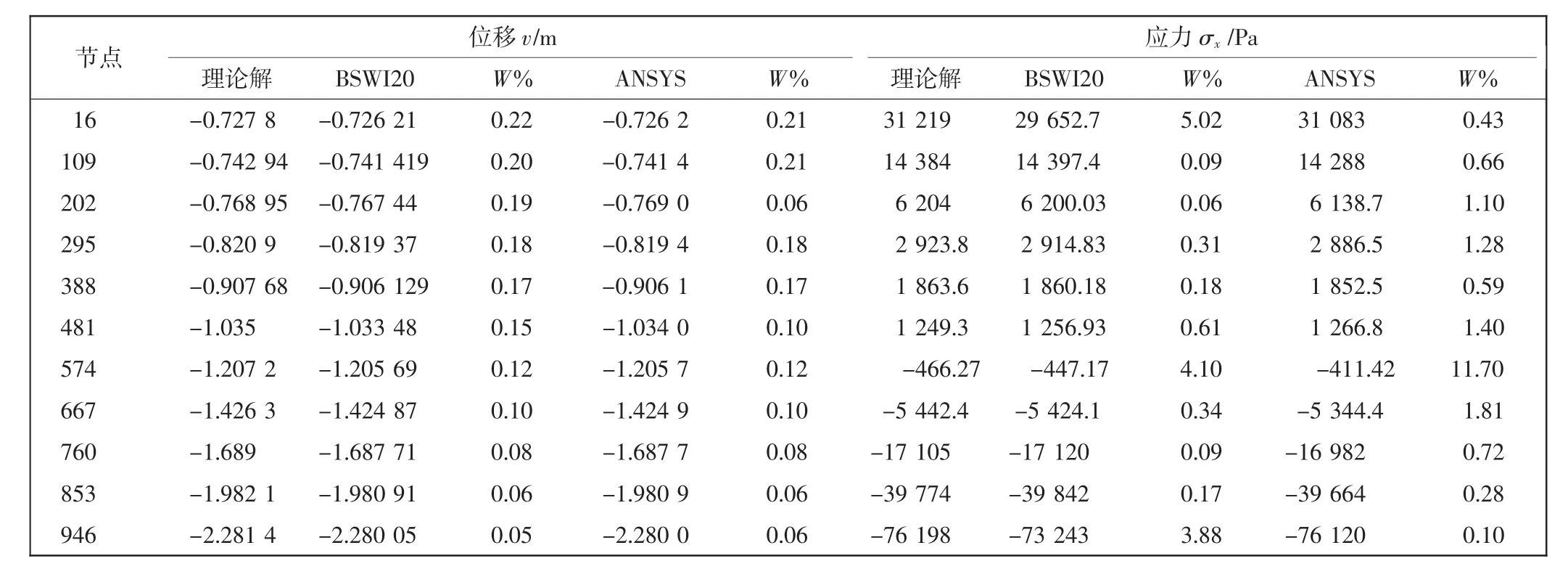
表1 用BSWI20插值的位移v和应力σx计算结果及其与理论解的误差Tab.1 Result and error of displacement v and stress σxfor BSWI20 interpolation

表2 用BSWI40插值的位移v和应力σx计算结果及其与理论解的误差Tab.2 Result and error of displacement v and stress σxfor BSWI40 interpolation

通过分析表1和表2可以注意到，位移和应力的误差均在允许范围之内。所以本文构造的简化小波杂交应力元是正确的，并且在划分较少网格情况下本文的算法更加精确，特别是用4阶样条小波函数所得结果。观察ANSYS所得应力结果，发现在正负应力交替的地方，误差突然变大，说明在此节点位置有一定的奇异性，而传统有限元在网格划分较少的情况下不能准确地将这一变化刻画出来，本文算法可以较为真实地反映此处应力变化情况。同时还可看出，位移求解精度很高，而应力求解结果与理论解相比误差较大，其原因在于由位移结果所产生的应力是通过式（1）和式（3）微分运算得到的。

算例2 将算例1所建立的模型用不同的网格数进行分析，比较在划分不同网格的情况下，最大位移计算结果与理论结果的误差百分比。本例没有对最大应力进行比较，因为应力是采用位移结果且通过式（1）和式（3）微分运算得到的，所以只用位移的精度来说明此方法的正确性。最大位移v的比较结果如表3和表4所示（其中理论解：最大位移v=-2.281 4）。

表3 2阶小波函数在不同网格数下的最大位移vTab.3 Maximum displacement v of 2-order wavelet function in different grid numbers

表4 4阶小波函数在不同网格数下的最大位移vTab.4 Maximum displacement v of 4-order wavelet function in different grid numbers

从表3和表4可以看出，两种小波尺度函数构造的插值函数都能使计算结果非常精确，说明此种简化的小波杂交应力元的构造是正确的。

由表3和表4比较，随着划分网格数的增加，由两种小波杂交应力元所计算的最大位移结果与理论解的误差呈逐渐减小趋势。而且在相同网格数的情况下，4阶小波尺度函数构造的杂交应力元计算结果比2阶的计算结果更加准确，说明高阶样条小波的尺度函数作为插值函数与杂交应力元结合具有优越性。

4 结语

本文为区间B样条小波有限元提出了一种简化的位移模式，即将矩阵形式换成了函数运算，并与杂交应力元结合，构建了简化的小波杂交应力元。最后，通过对二维弹性方形板应力和位移的计算结果进行分析，验证了该小波杂交应力元的正确性和优越性。可以得出，阶次高的区间小波用较少的网格就能得到理想结果，节省单位刚度矩阵形成、方程求解、网格划分的计算时间。网格数目越大，计算结果越精确。

[1]SWELDENSW.Wavelets：what next[J].IEEE，Proceeding of the IEEE，1996，4：680-685.

[2]何正嘉，陈雪峰.小波有限元理论及其工程应用[M].北京：科学出版社.2006.

[3]卞学鐄.杂交应力有限元法的研究进展[J].力学进展，2001（3）：344-349.

[4]吴长春，黄茂光.杂交有限元进展[J].自然科学进展，1999（12）：3-10.

[5]刘艳红，商中新.区间B样条小波杂交应力元分析及其应用[J].中国民航大学学报，2013，31（2）：75-79.

[6]PIAN D P CHEN.On the suppression of zero energy deformation modes[J].Int J Numer Methods Engng，1973，19（12）：1741-1752.

[7]谭德坤，孙 辉，付雪峰.基于小波有限元的平面问题求解方法[J].河北工程大学学报（自然科学版），2008（3）:106-109，112.

[8]韩建刚.小波有限元理论及其在结构工程中的应用[D].西安：西安建筑科技大学，2003.

[9]TIMOSHENKO S P，GOODIER J N.Theory of Elasticity[M].3rd ed.New York:McGraw-Hill Press，1970.

（责任编辑：杨媛媛）

Simplified interval B-spline wavelet on interval hybrid stress element

QING Guang-hui，ZHANG Chun-chao
（College of Aeronautical Engineering，CAUC，Tianjin 300300，China）

Combining with the hybrid stress finite element theory，based on 2-order/4-order 0 scale wavelet functions，a type of shape function is presented and the process of computer is reduced.The shape function can overcome the difficulty of unknown number increase exponentially with 2 to the power of n.In order to verify the correctness of current formulation，the median displacement and stress of 2-D elastic rectangular plate under uniformly distributed load is analyzed with different meshes.With the same mesh，the results of 4-order wavelet function are more accurate than that of 2-order wavelet function.

finite element；hybrid stress element；wavelet function；shape function

O343.1

：A

：1674－5590（2015）06－0050－05

2014-12-15；

：2015-01-04

：国家自然科学基金项目（60979001）

卿光辉（1968—），男，湖南新化人，教授，博士，研究方向为结构力学.