基于VegaPrime的航天器发射轨迹仿真

2015-03-05中南林业科技大学李东杨袁晓红

电子世界 2015年19期

中南林业科技大学李东杨袁晓红

中南林业科技大学李东杨袁晓红

【摘要】航天技术迅猛发展，推动了航天器仿真研究的深入。航天器航行轨迹仿真，对航天器飞行轨道设计起着重要的参考作用。本文采用改进型PID（Proportion Integration Differentiation）控制算法，通Creator对航天器建模，实现了在不失精度和效率的前提下，对航天器的三维弹道进行跟踪控制和仿真，有效的提高了航天器轨迹仿真的执行效率[1]。实验证明，本算法安全可靠，仿真模拟在执行效率和仿真精度上都有着良好的表现，在算法应用上对航天器的发展和航天器轨迹的优化都有着一定的理论参考和指导意义。

【关键词】计算机应用技术；航天器；轨迹仿真；VegaPrime

1 引言

随着导弹和航天器实验技术的发展，航天器轨迹仿真技术也得到相应的提高。由于航天器轨迹控制的运算量大、综合因素多，仿真过程中需要进行大量的精确计算，在加大了对计算机性能要求的同时，也降低了计算机仿真的执行效率[2-3]。专家们一直在寻找提高计算精度、降低运算次数的有效方法。

Brusch（1977）提出用经典增光拉格朗日法解决航天器轨道最优化问题，即通过交替的求增广函数相对应自变量的最小值来求解并修正拉格朗日乘子以实现航天器轨道的最优化。Well和Tandon（1982）把递归二次规划用到三维弹道最优化上，理论上虽然可行，但由于收敛速度慢，影响了运行效率[4-6]。杨永安（2004）对运载火箭仿真方面进行了实验，虽然达到了实时控制的要求，但是缺乏良好的精度。祁永强（2011）用双模型直接配置法对航天器轨迹进行优化，将最优化问题转换为非线性规划问题，优化了运行速率的同时也产生了不稳定性。

图1 航天器物理结构模型

本文以VegaPrime为平台，在传统的PID控制算法基础上进行适当的改进，力图提高仿真效率和仿真精度[7]。使用PID算法与非线性最优化技术相结合的方法，对航天器的轨迹控制进行仿真和模拟，解决了以往算法运算效率低、执行效率差等问题，为计算机仿真在航天器上的应用提供了良好的解决方案。

2 航天器物理模型结构

航天器一般由三级运载火箭助推产生动力，每一级在不同时间完成不同任务，如图1所示。

每一级火箭由燃料和航天器外壳两部分组成，分别用mpi和msi表示，其中，i表示火箭级数。

航天器的质量M为：

（1）式中，P为运载卫星的质量。

火箭刚启动时，由一级火箭提供动力，为整个航天器提供加速度；当一级火箭脱离后，余下的质量为二级火箭、三级火箭和运载卫星的质量；同理，其他各级火箭依次脱离后，飞行器质量有运载卫星和未脱离的火箭及其剩余燃料构成。在航天器飞行过程中，需根据航天器所处的阶段，使用不同的计算方法来控制航天器的轨迹。

3 基于PID算法的发射阶段轨迹控制与分析

3.1 模型参数与变量描述

现实中，飞行器是三维立体的。为了简化分析与计算，本文将三维模型平面化，用二维的视角来对三维的物体进行局部分析，再将分析结果推广到三维空间中去，从而实现对三维航天器的动态仿真控制。

图2是航天器在刚逃离大气层后的路线轨迹示意图，为了对航天器进行时时仿真控制，本文对航天器进行受力分析，以获得每个不同时刻的航天器的状态函数。再通过状态函数，结合改进的PID算法，对航天器进行必要的轨迹仿真和控制。

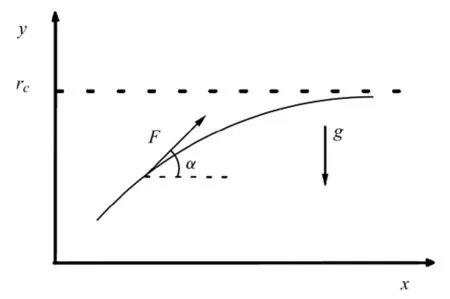
图2 飞行轨迹及受力示意

时间从t0（飞行器刚逃离大气层时刻为t0）开始记时，此时飞行器速度水平分量和垂直分量分别为Vx0合Vy0。经过时间t以后，航天器质量为Mt，飞行器受到的推力为Ft，速度的水平分量为vx，垂直分量为xy。

在二维平面中，当飞行器处于上升阶段时有：

当飞行器调整入轨道时，飞行器每秒消耗燃料为m：

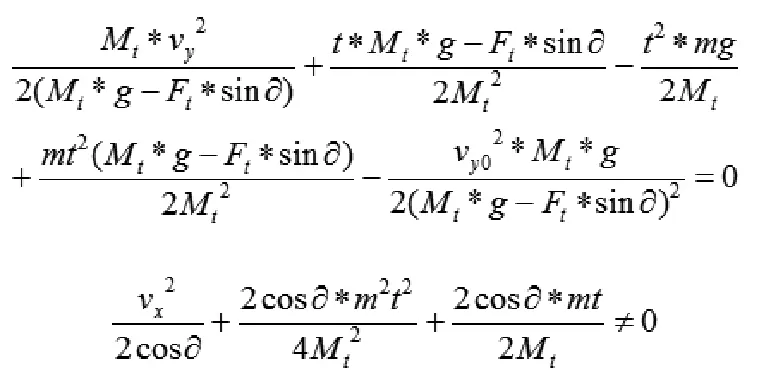
现实航天器物理分析十分复杂，如果把多项式建立的一次模型作为最终模型，将影响计算的精度，甚至会导致错误的数据，因此此模型只是作为基础模型，需要通过仿真不断的改善后得出二次模型。

3.2 PID算法的实现

PID是工业控制上的一种控制算法，其中P表示比例，I表示积分，D表示微分[8-9]。

由于飞行器的飞行轨迹不断变化，因此，对飞行器的实时控制就显得格外重要，为了简化控制复杂度，我们采用二维模型来进行分析，最后推广到三维中去。

离散公式：

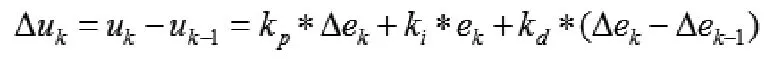
在PID增量算法中，由于执行元件本身是机械或物理的积分储存单元，如果给定值发生突变时，由算法的比例部分和微分部分计算出的控制增量可能比较大，如果该值超过了执行元件所允许的最大限度，那么实际上执行的控制增量将时受到限制时的值，多余的部分将丢失，将使系统的动态过程变长，因此，需要采取一定的措施改善这种情况。

纠正这种缺陷的方法是采用积累补偿法，当超出执行机构的执行能力时，将其多余部分积累起来，而一旦可能时，再补充执行。

4 仿真结果与分析

本文利用视景仿真软件VegaPrime进行仿真，仿真所使用的航天器模型均利用Creator软件建模。在仿真过程中，发动机尾焰是用粒子特效来进行虚拟仿真的，但是考虑到普通计算机性能有限，因此仿真中对涉及到的发动机尾焰的效果有所减弱。仿真实验使用的粒子特效参数见表1：

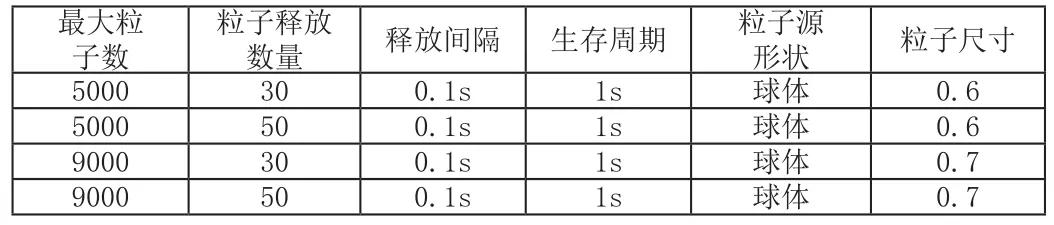
表1 粒子特效参数表

经过仿真测试，当最大粒子数量为9000；粒子释放数量为30；释放间隔为0.1秒；粒子生存周期为1秒；粒子源形状为球体，尺寸为0.7。

图3 航天器发射初始状态

图3是航天器发射初始阶段，此时航天器与地形平面垂直，仿真过程采用二次函数对航天器高度进行描述。当航天器达到一定高度（逃离大气层），则采用模型公式和PID算法对航天器进行控制。

图4 航天器飞行状态

图5 航天器入轨后状态

图4、图5分别为航天器逃离大气层和进入轨道的仿真结果。航天器逃离大气层后，按照预定轨道和控制算法进行飞行，期间航天器的位置信息和速度信息会实时反馈到控制台中，方便分析和判断。当航天器入轨后，本算法不在对航天器进行控制，航天器飞行状态将取决于其入轨前的状态，并将保持不变。

5 结论

本文基于VegaPrime仿真环境，利用改进的PID算法对航天器发射轨迹进行仿真[10]。该模型综合了机理模型和经验模型的建模方法，对二维模型进行分析，然后推广到三维仿真中去，最终实现航天器轨迹模拟三维展示。在不失精度的前提下，本文忽略了一部分次要因素，简化了建模过程，避免了大量复杂的物理运算和参数调试。经过软件测试，上述模型是一个可靠的、完整的系统模型，可以对航天器轨迹进行描述，适合于对航天器轨迹仿真的研究。

参考文献

[1]贾沛然,陈克俊.远程火箭弹道学[M].长沙:国防科技大学出版社,1993.

[2]康志宇,等.基于STK的导弹飞行数据快速可视化仿真实现[J].弹箭与制导学报,2004(2):1-4.

[3]廉莉莉,等.空间对接过程动画仿真系统的设计与实现[J].航天控制,2004(2):26-30.

[4]和平鸽工作室.OpenGL高级编程与可视化系统开发(高级编程篇)[M].北京:中国水利水电出版社,2003.

[5]白建军.OpenGL三维图形设计与制作[M].北京:人民邮电出版社,1999.

[6][美]David J Krug linsk等.Visual C ++ 6.0内幕[M].北京:希望电子出版社,1999.

[7]Robert Armellin,Michele Lavagna,Ryan P Starkey,et al.Aerograviyy-assist maneuvers:coupled trajectory and vehicle[J]. Journal of Spacecraft and Rockets,2007,50(168):113-120.

[8]Ratnaweera A,Halgamuge S K,Wat sonH C.Sel-f organizaing hierarchical particle swarm iptimizer with timevarying accelerat ion coeff-i cients[J].IEEE t ransaction on evolutionary comput ation,2004,8(3):240-255.

[9]孙丕忠,夏智勋,郭振云.水平空中发射固体运载火箭轨道设计与优化[J].固体火箭技术,2004,27(2):87-90.

[10]Hadjisavvas N,Pardalos P.Advances in Convex Aanlysis and Global Optimization[M].The Netherlands: Kluwer Academic Publishers,2001.