粘贴加固混凝土氯离子扩散的理论模型和数值模拟
2015-03-05姚未来江世永李雪阳
姚未来,江世永,飞 渭,李雪阳
(后勤工程学院a.军事土木工程系;b.训练部,重庆401311)
氯盐环境下,氯离子侵蚀混凝土是引起钢筋锈蚀的主要原因,降低结构耐久性。高丽燕等[1]基于实际海洋环境,研究了力学荷载作用下混凝土中的氯离子扩散性能。张俊芝等[2]采用现场取芯试验分析了既有水闸闸墩混凝土的氯离子侵蚀规律。王元战等[3]通过盐雾试验总结了受荷混凝土的氯离子扩散规律,拟合了氯离子扩散荷载影响系数与构件应力状态之间的关系式。Bogas等[4]通过试验研究了氯离子在不同种骨料混凝土中的扩散规律。Muthulingam等[5]提出了三参数模型描述氯离子在粉煤灰混凝土中的扩散,预测值与试验值符合较好。Van等[6]研究了干湿循环下混凝土中氯离子的扩散规律,并讨论了孔隙水对扩散过程的影响。目前,国内外对混凝土中氯离子的扩散虽进行了广泛研究,但分析对象均是未加固混凝土,未见针对加固混凝土的氯离子扩散研究报道。
Collepardi等[7-8]首先提出用 Fick第二定律描述氯离子在混凝土中的扩散,其基本假设是:1)混凝土是半无限大均匀介质;2)氯离子在混凝土中的扩散是一维扩散;3)不考虑氯离子与混凝土产生吸附、结合;4)认为扩散系数、边界条件(暴露表面的氯离子浓度)为常数。研究证明,简单采用以上假设的计算结果不理想[9]。针对Collepardi等提出的氯离子扩散模型,学者们提出了各项修正。利用修正的Fick第二定律扩散模型可对氯离子扩散进行数值模拟,但现有模拟在考虑扩散边界条件、外荷载、环境、混凝土自身劣化等影响因素方面尚不完善,尚未在数值模拟中较全面地考虑各项修正[10]。本文基于修正的Fick第二定律扩散模型,较全面考虑各项修正,并考虑外粘贴加固对扩散的影响,利用多种方法对大气盐雾环境下粘贴加固混凝土梁的氯离子扩散过程进行数值模拟。
1 修正的Fick第二定律
根据Thomas等[11]的研究,考虑氯离子扩散系数的时变性。为同时反映环境、荷载效应、混凝土自身劣化的影响,在理论建模时,引入综合劣化效应系数计算混凝土的等效扩散系数[12]。进入混凝土的氯离子在扩散过程中将产生结合作用,自由氯离子导致钢筋锈蚀,氯离子的结合性一定程度上降低了自由氯离子的数量,在氯离子扩散过程中需考虑氯离子的结合性。根据以上修正,提出新的扩散方程。
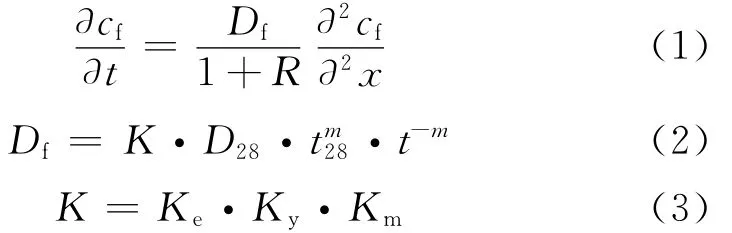
式中:cf、Df为自由氯离子的浓度、扩散系数;K为综合劣化效应系数;Ke、Ky、Km分别为扩散的环境劣化系数、荷载劣化系数、材料劣化系数。t28为28d龄期,m为经验参数,参数R考虑氯离子的结合性。
令

在求换元参数T时需要对等式右边积分,积分下限的含义是氯离子开始扩散进入混凝土的时间起始点,取混凝土开始浇筑制作的时刻为0时刻,浇筑后28d为养护期,忽略养护期间由外界进入混凝土的氯离子,扩散时间起始点取为第28d。根据Tang等[13]的研究,对(5)式两边积分可得
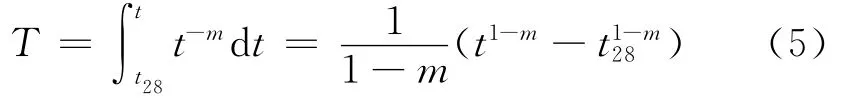
整理(2~5)式,可得
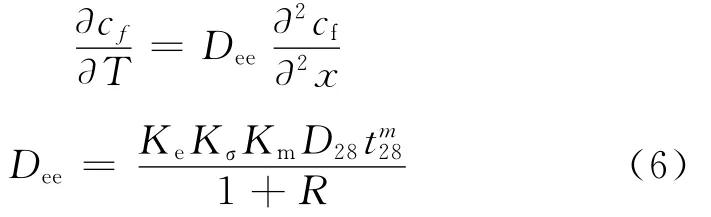
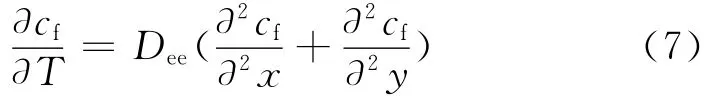
根据Fick第二定律,研究扩散过程需要求解偏微分方程式(7)。求解需要方程的边界条件,即混凝土暴露边界的氯离子浓度。大量检测结果表明,氯盐环境中混凝土表面的氯离子浓度值并不是恒定值,它随着时间逐步累积并最终达到稳定[14]。
描述混凝土表面氯离子浓度随时间的的变化规律主要有线性、平方根型、幂函数型、对数型和指数型,具体函数表达式见表1。表中c1、c0为拟合的氯离子浓度,单位为%;k,α,r为拟合系数。采用Costa等[15]提出的幂函数型的拟合精度较高,作为时间边界条件比较符合实际[9]。
式(6)即为修正之后的氯离子扩散方程,其形式完全与Fick第二定律一致,分别称Dee、T为名义扩散系数与名义扩散时间。本文算例中混凝土梁的氯离子扩散视为二维扩散,方程为

表1 边界条件表达式Table 1 Boundary Conditions
2 粘贴加固对扩散的影响
目前,对氯离子侵入混凝土进行了较多试验研究与理论分析,但均针对未加固混凝土,经查未发现加固构件的氯离子扩散分析,研究氯离子在粘贴加固混凝土梁中的扩散。粘贴法加固利用粘结胶将加固材料可靠粘结于构件表面,提高构件承载力与刚度,在实际工程中运用广泛。本文算例中的加固构件采用环氧树脂将CFRP片材粘贴于梁底面。
加固中使用的环氧树脂具有较好的密封性。张伟平等[16]通过试验测量氯盐环境下混凝土的累计电量、吸水率,发现明环氧树脂涂层可使饱水状态下混凝土氯离子扩散速度和非饱水状态下混凝土由于毛细吸附引起的氯离子传输能力显著降低。谷坤鹏等[17]通过试验研究表明,环氧树脂表面涂层可显著提高混凝土的抗氯离子渗透性能,使混凝土电通量大幅度下降,几乎可忽略氯离子的扩散作用。大量的试验为保证氯离子进入混凝土试件为一维扩散,均采用环氧树脂涂抹在试件其他非扩散表面起密封作用[18-20]。
本文算例中讨论的加固混凝土梁在梁底面涂抹环氧树脂,涂层外表面粘结碳纤维片材,整个构件处于大气盐雾环境中,考虑到环氧涂层较好的密封性与外部存在的碳纤维片材,忽略穿过加固纤维片材与环氧涂层进入主体混凝土的氯离子。将粘贴加固行为考虑为对氯离子扩散路径的阻断,通过适当变换扩散方程的初值条件与边界条件模拟氯离子扩散进入粘贴加固混凝土梁。对于非粘贴加固混凝土则不考虑以上边界条件的变换,故上述修正的氯离子扩散模型均可用于描述非加固、加固混凝土的扩散规律。
3 修正的扩散模型的验证
基于修正的Fick第二扩散定律,采用一维扩散模型计算结果与Thomas等[11]的实测数据进行对比,如图1(a);采用二维扩散模型计算结果与张伟等[21]的实测数据进行对比,如图1(b)。结果表明氯离子环境中的混凝土结构的氯离子浓度实测值与理论预测模型较好地相符合。
上述 Thomas等[11]、张伟等[21]的实测数据虽均针对未加固混凝土,但修正的氯离子扩散模型已能较好地描述氯离子在混凝土中的扩散过程,有明显的合理性和可用性。本文基于该理论模型,同时,考虑边界条件的变换,对氯离子在粘贴加固混凝土梁中的扩散进行数值模拟。
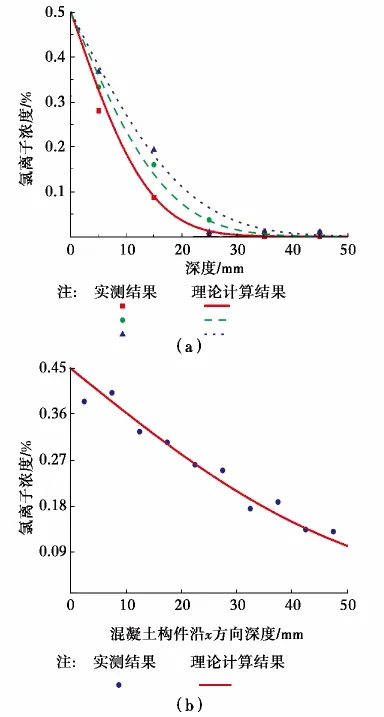
图1 扩散理论模型的验证Fig 1 Verification of Revised Model
4 数值模拟算例
4.1 构件基本信息及参数选取
本算例模拟沿海盐雾环境下粘贴加固混凝土梁的氯离子扩散过程,基于上述修正的Fick第二定律,采用二维扩散模型进行计算。该加固梁所处的沿海环境常年空气湿润,假定混凝土近似处于水饱和状态,内部相对湿度为100%,氯离子在混凝土内的传输方式以扩散为主,以下是构件基本信息。
梁截面尺寸为:高500mm,宽200mm,上表面与现浇板相连,处于封闭状态。加固之前,氯离子从两个侧面、一个底面扩散进入。加固之后,底面粘贴加固材料,阻断扩散路径,氯离子不再从底面进入,继续从两侧扩散进入,如图2~3所示。
算例中的混凝土配合比、扩散系数、暴露边界浓度取用Thomas等[7]的实测数据,如表3~4。
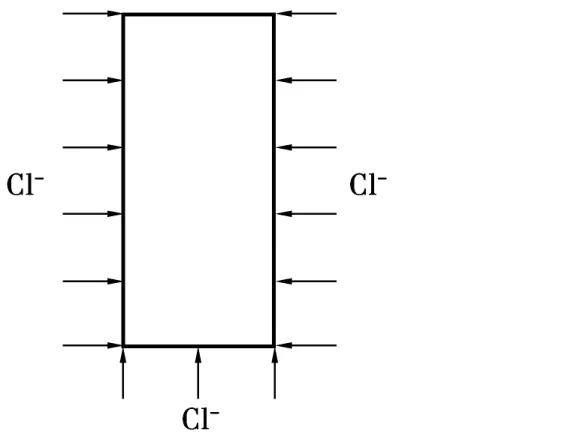
图2 加固前侵入情况Fig 2 Invasion before strengthening
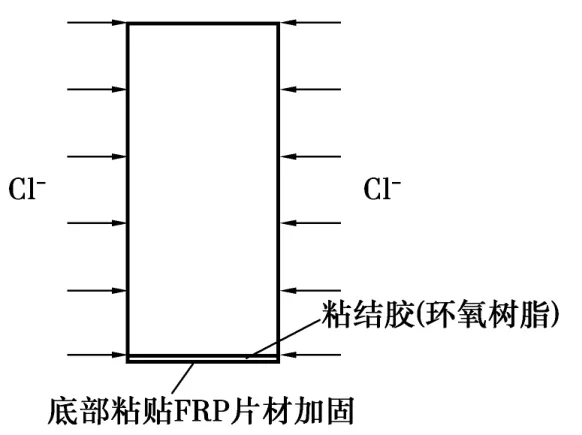
图3 加固后侵入情况Fig 3.Invasion after strengthening

表3 算例中混凝土的配合比Table 3 The mix proportion of concrete(kg·m-3)

表4 算例边界条件取值Table 4 The values of boundary conditions
用幂函数Cs=C1tn对表4中的实测数据进行拟合,可得
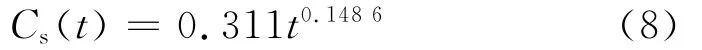
根据实测数据,取D28=6×10-12m2/s。
根据文献[22],考虑氯离子结合能力时,取参数R=2.14。考虑大气氯离子扩散的差异性,参考文献[23],取盐雾环境系数Ke=0.72。取材料劣化系数Km=2[21]。由Zhang等[24]的试验结论考虑外加弯曲荷载对氯离子扩散的加速效应。Zhang等[24]发现弯曲荷载使混凝土受拉区裂缝不断开展,加剧受拉区损伤程度,导致氯离子更快进入混凝土。考虑荷载效应时,为保持Fick第二定律的均匀性假定,将扩散系数适当放大,引入荷载劣化系数Ky。
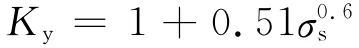
式中:σs为混凝土梁外加弯曲荷载与极限抗弯承载力的比值。若取加固前σs为0.6,则加固前荷载增大系数Ky1=1.375;实施粘贴加固时,对原混凝土梁卸载并修补裂缝,加固完成后继续受荷载作用,考虑加固引起构件刚度增加,受拉区变形较加固前减小,微裂缝部分闭合,氯离子传输速度较加固前降低,若取加固后σs为0.3,则加固后荷载增大系数Ky2=1.248。
由以上参数取值,可求得名义扩散系数Dee与名义扩散时间T,算式中的时间均以年为单位。
加固前:
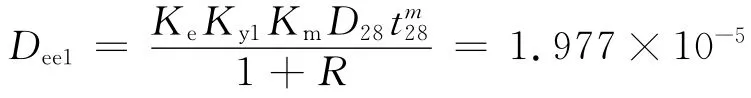
加固后:
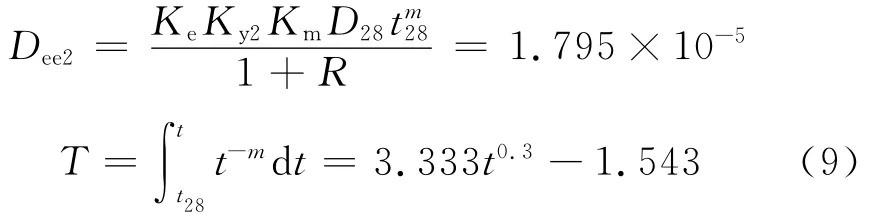
将式(9)代入(8)得出边界条件与名义扩散时间的关系:
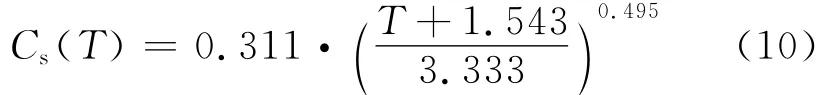
4.2 计算方法与结果讨论
本算例计算构件暴露时间为15、20、25a的氯离子扩散情况,构件于第10a实施加固。梁两个侧面在加固前、后始终处于暴露敞开状态,氯离子可一直由两侧面进入混凝土;梁底面仅在加固前有氯离子进入。加固后的计算以未加固混凝土梁第10a内部的氯离子浓度作为初始条件,边界条件考虑为氯离子仅继续从两个侧面进入,底面封闭。将扩散视为二维扩散,通过有限元法求解扩散方程(7)。采用通用商业有限元分析软件ABAQUS、MATLAB自编程、MATLAB PDE tool 3种途径求解。
4.2.1 具体算法 1)采用通用商业软件ABAQUS求解。利用物质扩散方程与非稳态传热方程之间的相似性,用ABAQUS求解方程(7)。文献[25]指出了物质扩散方程与非稳态传热方程之间的参数对应关系,取温度T=C,密度ρ=1,比热cp=1,则热传导系数λ=热扩散率a=扩散系数Dee。则此时非稳态传热方程与氯离子扩散方程为同一个偏微分方程,即可以利用ABAQUS热分析模块进行氯离子扩散问题分析[20]。将混凝土梁截面均匀划分为1 000个网格,边界条件采用式(10)表示,构件加固之后,取消梁底部边界条件继续计算。2)Matlab自编程计算。通过对扩散方程(7)按伽辽金处理可将偏微分方程转化为常微分方程组进行求解,网格划分与1)相同,常微分方程组如下:
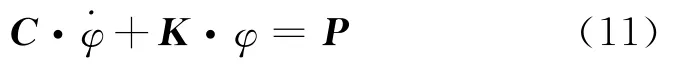
式中:C矩阵为氯离子的容量矩阵,K矩阵为氯离子扩散矩阵,P为浓度荷载矩阵,当取强制性边界条件时可忽略P矩阵。利用高斯积分后可求出单元刚度矩阵,装配后可求得整体刚度矩阵K,C。代入(11),运用数值方法可求得浓度矩阵,边界条件变换方式与1)相同。3)Matlab PDE tool求解。利用MATLAB中的偏微分方程工具箱PDE tool可直接求解二维扩散方程式(7)。偏微分方程形式取抛物线型,输入名义扩散系数Dee与时变性边界条件式(10),迭代求解,边界条件变换方式与上述一致。
4.2.2 计算结果与讨论 用以上3种方法计算加固构件内的氯离子浓度,扩散时间为15、20、25a,输出距梁暴露底面分别为0、0.01、0.02、0.03、0.04、0.05、0.06m的氯离子浓度值,以上各点距左侧面0.03mm,位置见图4。取混凝土梁的保护层厚度为30mm,钢筋位置在图中标出。
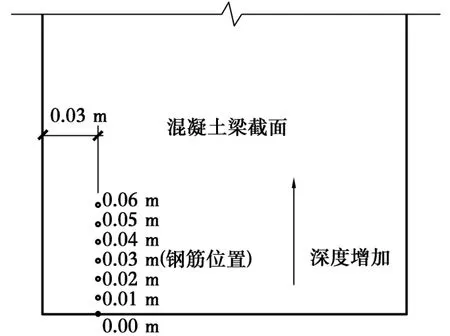
图4 各点位置分布Fig 4 Location of points and steel bar
1)计算结果
构件于第10a进行粘贴加固,3种算法计算结果如下图5。
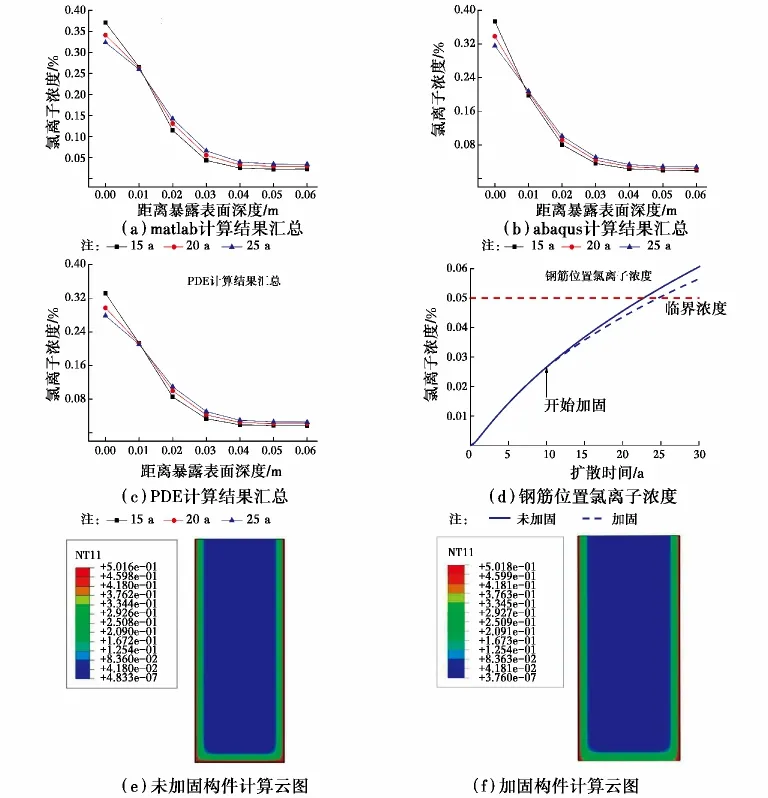
图5 计算结果Fig 5 Calculation result
由图5(a)~(c),加固构件随着深度增加,各点的氯离子浓度呈下降趋势。随着扩散时间的推移,梁底面点的氯离子浓度逐渐降低,距离表面0.01 mm的点在加固后15a内浓度变化不明显,其他深度区域的氯离子浓度随着时间推移逐渐增加。由图5(d),加固后钢筋位置的氯离子浓度与浓度上升幅度均较未加固降低,曲线向下偏移,钢筋达到锈蚀临界浓度的时间有所推迟。氯离子浓度达到临界浓度时,钢筋开始锈蚀,临界浓度可用于构件剩余寿命评估。
2)结果讨论
图6为氯离子的扩散示意图,根据物质扩散的特性,物质将从浓度较高的位置往浓度较低的位置迁移。图中A、B、C 3点氯离子的浓度分别为CA、CB、CC,CA>CB>CC。B点的氯离子将向浓度更低的C点迁移,B点浓度值降低;A点的氯离子将向浓度较低的B点迁移,B点浓度值升高。B点氯离子浓度变化是这两个效应的综合。
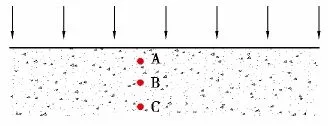
图6 氯离子扩散示意图Fig 6 The schematic diagram for chloride diffusion
由图5(a)~(c)可知,对于加固构件,粘贴加固边界部位的氯离子浓度在加固后逐年减少。这是由于粘贴加固对梁底面有较好的密封用,切断了氯离子从混凝土梁底面进入构件的扩散路径,改变了边界条件,氯离子只有通过两侧扩散进入到达底面补充浓度;同时,边界各点的氯离子又向更深处浓度较低的位置扩散,从两侧边界补充的氯离子数量少于扩散流失的氯离子,导致边界各点的氯离子浓度逐年减低,出现稀释现象,见ABAQUS计算云图,图5(e)~(f)分别表示未加固、加固构件的氯离子扩散情况。如图7所示,加固后底面边界的氯离子浓度逐年降低。
由图5(a)~(c),可推断距表面0.01m的位置在加固后15a内,氯离子流失与补充基本相当,浓度无太大变化。距表面0.02~0.06m的位置,加固后氯离子补充量仍大于流失量,浓度随时间上升。

图7 边界氯离子浓度变化Fig 7 Concentration of the point at interface
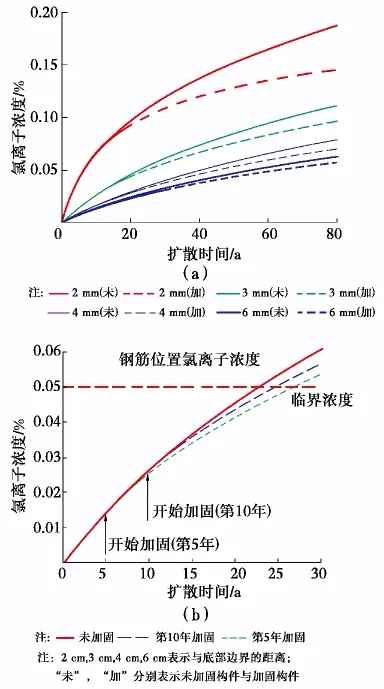
图8 各点氯离子浓度变化Fig 8 Chloride concentration of points
图8 (a)给出未加固与加固构件各点的浓度变化情况,可见粘贴加固一定程度上降低了混凝土内部各点的氯离子浓度。图8(b)为未加固、加固构件钢筋位置氯离子浓度随时间变化的曲线。粘贴加固推迟了钢筋表面氯离子浓度达到临界浓度的时间,延缓了钢筋锈蚀,一定程度上提高了材料寿命。图中分别表示了未加固、第5a加固、第10a加固的钢筋位置的氯离子浓度变化曲线。第5a加固比第10 a加固更大程度上降低了钢筋位置氯离子的浓度,更长地推迟了氯离子浓度达到钢筋锈蚀临界浓度的时间。
取钢筋锈蚀的氯离子临界浓度0.05%(相对于混凝土质量),根据图8(b)计算的浓度变化曲线,用多项式进行拟合,以解析方式求出未加固、第5a加固、第10a加固的构件,钢筋位置浓度达到临界浓度的时间,可用于粘贴加固构件的寿命预测,见表5。
由表5可得,相比于未加固构件,加固后钢筋位置氯离子浓度达到临界浓度时间有了不同程度延后,第5a加固延后了4.46a,第10a加固延后了1.99a。

表5 钢筋位置氯离子浓度增长曲线拟合及到达临界浓度时间预测Table 5 Curve fitting & Time to corrosion
5 结 论
1)综合考虑扩散系数、边界条件的时变性;氯离子的结合性;混凝土的劣化效应;大气环境下氯离子扩散的差异性;扩散的多维性;粘贴加固对扩散边界条件的影响,提出修正的氯离子扩散理论模型,可用于计算氯离子在未加固、加固混凝土中的扩散。
2)将其他学者的实测数据与理论计算结果对比,验证了修正的扩散理论模型的合理性和可用性。
3)采用修正的扩散理论模型,通过ABAQUS、MATLAB PDE tool、MATLAB自编程3种方法均可对粘贴加固混凝土梁的氯离子扩散过程进行数值模拟。模拟结果表明,相比未加固构件,粘贴加固能降低钢筋位置的氯离子浓度值,减小浓度增长幅度,延缓氯离子浓度到达临界浓度的时间,提高材料使用寿命,加固时间越早,钢筋位置氯离子浓度达到临界浓度时间越推迟。
[1]高丽燕,万小梅,任心波.持续荷载下混凝土的氯离子扩散性能研究[J].混凝土与水泥制品,2012,(4):21-25.Gao L Y,Wan X M,Ren X B.The chloride diffusion in concrete under sustained load[J].China Concrete and Cement Products,2012,(4):21-25.(in Chinese)
[2]张俊芝,庄华夏,伍亚玲,等.临海既有混凝土氯离子侵蚀及钢筋初锈时间预测[J].建筑材料学报,2014,17(3):454-458.Zhang J Z,Zhuang X H,Wu Y L.Chloride ion erosion and prediction of initial corrosion time of steel bar in the existing coastal concrete[J].Journal of Building Materials,2014,17(3):454-458.(in Chinese)
[3]王元战,周海锋.盐雾环境下受荷混凝土中氯离子扩散试验[J].材料科学与工程学报,2013,31(5).Wang Y Z,Zhou H F.Chlorine ion diffusion experiment in loaded concrete under salt spray environment [J].Journal of Materials Science and Engineering,2013,31(5).(in Chinese)
[4]Bogas J A,Gomes A.Non-steady-state accelerated chloride penetration resistance of structural lightweight aggregate concrete [J].Cement and Concrete Composites,2015,60:111-122.
[5]Muthulingam S,Rao B N.Consistent models for estimating chloride ingress Parameters in fly ash concrete[J].Journal of Building Engineering,2015,3:24-38.
[6]van der Zanden A J J,Taher A,Arends T.Modelling of water and chloride transport in concrete during yearly wetting/drying cycles[J].Construction and Building Materials,2015,81:120-129.
[7]Collepardi M,Marcialis A,Turriziani R.The kinetics of penetration of chloride ions into the concrete[J].cemento,1970,67(4):157-164.
[8]Collepardi M,marcialis A,turriziani R.Penetration of chloride ions into cement pastes and concretes[J].Journal of the American Ceramic Society,1972,55(10):534-535.
[9]余红发,孙伟.混凝土氯离子扩散理论模型[J].东南大学学报:自然科学版,2006:68-76.Yu H F,Sun W.Model research on chlorine ion diffusion in concretes [J].Journal of Southeast University:Natural Science Edition,2006:68-76.(in Chinese)
[10]施钢.混凝土中氯离子三维扩散模型及参数拟合[J].厦门理工学院学报,2014,22(1):80-85.Shi G.A 3Dmodel of chloride ion diffusion in concrete and determination of its parameters[J].Journal of Xiamen University of Technology,2014,22(1):80-85.(in Chinese)
[11]Thomas M D A,Bamforth P B.Modelling chloride diffusion in concrete:effect of fly ash and slag[J].Cement and Concrete Research,1999,29 (4):487-495.
[12]余红发.盐湖地区高性能混凝土的耐久性、机理与使用寿命预测方法[D].南京:东南大学,2004.Yu H F.The durability,mechanism and life prediction of high performance concrete in salt lake region[D].Nanjing:Southeast University,2004.(in Chinese)
[13]Luping T,Gulikers J.On the mathematics of timedependent apparent chloride diffusion coefficient in concrete[J].Cement and Concrete Research,2007,37(4):589-595.
[14]赵羽习,王传坤,金伟良,等.混凝土表面氯离子浓度时变规律试验研究[J].土木建筑与环境工程,2010,32(3):8-13.Zhao Y X,Wang C K,Jin W L.Experimental analysis on time-dependent law of surface chloride ion concentration of concrete [J].Journal of Civil,Architecture & Environmental Engineering,2010,32(3):8-13.(in Chinese)
[15]Costa A, Appleton J.Chloride penetration into concrete in marine environment-Part II:Prediction of long term chloride penetration[J].Materials and Structures,1999,32(5):354-359.
[16]张伟平,管小军,任佳俊,等.环氧涂层对混凝土抗氯离子渗透性能的影响[J].建筑材料学报,2008,11(3):339-344.Zhang W P,Guan X J,Ren J J.Experimental study on chloride permeability of concrete surface-treated with epoxy resin[J].Journal of Building Materials,2008,11(3):339-344.(in Chinese)
[17]谷坤鹏.矿渣与涂层对混凝土抗氯离子侵蚀的影响[J].低温建筑技术,2008,30(2):16-18.Gu K P.The impact of slag and epoxy resin to chloride ion diffusion in concrete [J].Low Temperature Architecture Technology,2008,30(2):16-18.(in Chinese)
[18]Farahani A,Taghaddos H,Shekarchi M.Prediction of long-term chloride diffusion in silica fume concrete in a marine environment [J].Cement & Concrete Composites,2015:10-17.
[19]Li G,Yang B,Guo C,et al.Time dependence and service life prediction of chloride resistance of concrete coatings[J].Construction &Building Materials,2015:19-25.
[20]Farahani A,Taghaddos H,Shekarchi M.Prediction of long-term chloride diffusion in silica fume concrete in a marine environment [J].Cement & Concrete Composites,2015:10-17.
[21]张伟,董志良,吕黄.混凝土氯离子二维扩散模型及工程验证[J].水运工程,2009,(6):35-39.Zhang W,Dong Z L,Lv H.Two-dimensional model for chloride diffusion in concrete and engineering verification[J].Port & Waterway Engineering,2009,(6):35-39.(in Chinese)
[22]余红发,孙伟,鄢良慧,等.混凝土使用寿命预测方法的研究I—理论模型[J].硅酸盐学报,2002,(6):686-690.Yu H F,Sun W,Wu L H.Study on prediction of concrete service life I-theoretical model[J].Journal of Chinese Ceramic Society,2002,(6):686-690.(in Chinese)
[23]刘军,邢锋,董必钦,等.盐雾环境下氯离子在混凝土中的扩散[J].深圳大学学报:理工版,2010,27(2):192-198.Liu J,Xing F,Dong B Q.Diffusion of chloride ion into concrete under salt spray environment[J].Journal of Shenzhen University:Science and Engineering,2010,27(2):192-198.(in Chinese)
[24]Zhang Y,Sun W,Liu Z,et al.One and two dimensional chloride ion diffusion of fly ash concrete under flexural stress [J].Journal of Zhejiang University Science A,2011,12(9):692-701.
