压缩感知理论及其电能质量应用与展望

朱云芳，戴朝华，陈维荣，何正友

（1.西南交通大学电气工程学院，成都610031；2.国家轨道交通电气化与自动化工程技术研究中心，成都610031）

电力系统电能质量对生产、社会和经济影响很大，一直备受工程学术界、电力用户和电力公司的关注。随着电网中大量电力电子设备和非线性负荷的应用，使得电能质量问题日益突出，对电能质量进行有效监测和分析愈显重要[1-3]。

现有的电能质量监测系统都基于Nyquist 采样定理，一方面，要求采样速度快，特别是对于高次谐波和各种瞬态扰动，要求采样间隔达毫秒甚至微秒级，硬件要求较高；另一方面，大量的数据，给信号分析与处理带来了极大挑战，同时为了存储和传输，还需要大量压缩编码计算[4，5]，数据利用率及效率低[6]。

对于电能质量扰动信号分析，现有方法主要有傅里叶变换、小波变换、S 变换、Hilbert-Huang 变换HHT（Hilbert-Huang transform）等[7]。傅里叶变换主要用于分析稳态信号，对于非平稳信号不具有时间局部性，不能满足时频分析的要求，而且存在频谱泄漏和栅栏效应等问题；小波变换的性能与采样率、小波基、分析频带的选择相关，缺乏自适应性[8]，而且会产生能量泄漏和频谱混叠现象，不能单独提取任意频次的信号，使其无法定量检测含噪、含谐波的扰动信号的幅值特征[9]；S 变换结果只包含若干个特定频率分量（由时间窗决定）在不同时刻的幅值信息，无法精确测量基波频率波动以及间谐波的特征参数[10]；HHT 能够得到解析的信号分解形式，且具有一定的自适应性，但这种算法同样不能表达不连续的信号，即要求所有信号成分都是从同一时刻开始并具有相同的时间支集[8]，同时HHT 通常利用经验模态分解EMD（empirical mode decomposition）能有效剥离各振荡模式，并对非线性模式有较好跟踪能力，但EMD 分解的物理意义尚不明确，缺乏判断固有模态分量为实际振荡模式还是虚假分量的理论依据，且没有给出算法观测时窗长度和模式分辨能力的定量分析[11]。

针对以上传统信号采样和信号分析方法的不足，国内外学者对此开展了大量研究。其中，时频原子稀疏分解和压缩感知CS（compressive sensing）理论成为最近的研究热点[12]，本文对两者及其在电力系统电能质量中的应用进行了综述与展望。

1 稀疏分解与压缩感知

连续信号f（t）∈H，H 为Hilbert 空间，将f（t）采样离散化转化为f（n）的形式。定义原子库D=（gr）r∈Γ，则信号f（n）可表示为

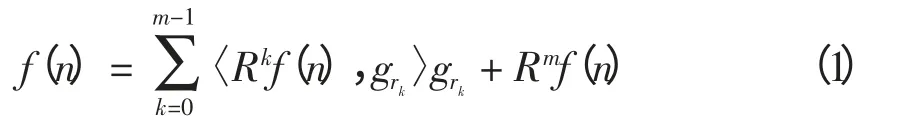
式中，grk和Rkf（n）分别为第k 次分解的时频原子和残差。如果分解m 次后达到所需的精度要求，则f（n）可由选择出来的原子近似线性表示，相应的分解过程称之为原子稀疏分解。

在稀疏分解基础上，近年来出现了一种新颖的理论—压缩感知[12，13]，又称压缩传感、压缩采样，其对于稀疏或可压缩的信号，突破了传统的Nyquist 采样定理。该理论认为，如果一维信号X∈яN在ψ 域是K-稀疏的（K〈〈N），采用一个与ψ 非相关的观测矩阵Φ：M × N（Φ 的每一行可以看作是一个传感器），对信号执行压缩观测，得到观测值Y∈яM（M〈〈N），即

式中：S∈яN，S = [s1，s2，…，sN]，且si=〈X，φi〉；φi为稀疏矩阵ψ 的第i 列，i∈{1，2，…，N}。则可以求解ℓ0-范数优化问题，即

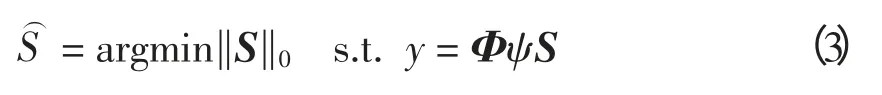
2 国内外研究现状

压缩感知理论将采样与压缩合并进行，有望少量采样就能恢复信号，不仅降低对硬件要求，而且提高压缩效率，大大减轻数据存储、传输和分析处理的压力。因此，一经提出，就引起了相关领域研究人员的高度关注和极大兴趣[12-17]，被美国科技评论评为“2007 年度十大科技进展”，理论提出者获得了“2008 年IEEE 1T 学会最佳论文奖”。

目前，CS 已用于压缩信息获取和压缩信号处理，短短5 年即广泛应用于光学/雷达成像、无线传感网络、图像采集设备的开发、医疗成像、模式识别、地质勘探、生物传感、超谱图像处理及遥感图像处理等众多领域。压缩信息获取考虑其物理实现，即采样方式，常用的包括模拟信息转换器采样、随机采样、随机滤波器、在AD 采样之后进行的压缩观测等[16]；压缩信号处理则用于信号压缩、检测、分类、估计和滤波等[18]。

不论是压缩信息获取，还是压缩信号处理，CS应用都存在3 个关键的基础问题：信号稀疏性、非相关观测和非线性优化重构[13-17]。其中，信号稀疏性是CS 的必备条件，由信号本身决定，算法上在于构建稀疏矩阵；非相关观测是CS 的关键，由感知系统和信号共同决定，归结为算法上的观测矩阵构建和硬件上的物理实现；非线性优化是CS 重建信号的手段，决定了压缩采样信号恢复的有效性和精度。

2.1 稀疏表示

稀疏表示是CS 理论应用的前提和基础，决定了压缩采样点个数、信号稀疏分解与重构的精度和计算复杂度。目前信号稀疏表示的研究主要集中在如何构造一个适合某一类信号的冗余字典和如何设计快速有效的稀疏分解算法。

1）稀疏字典

按照原子是否正交，可以分为正交基字典和超完备冗余字典。正交基字典一般由一个正交变换得到，如Fourier 变换、DCT 变换、沃尔什变换、小波变换等，其特点是构造简单、实现快速、表示过程的复杂度较低；但是，对于实际信号来说，这些固定的正交基往往不足以灵活表示复杂未知的信号特征，从而难以使信号在变换域足够稀疏。

超完备冗余字典中的原子远多于完备基中的元素，并且通过设计合适的算法，原子还可以根据信号的特点而改变，从而可以尽可能地逼近信号的结构，信号分解所得解向量也更稀疏，便于信号压缩、特征提取等。目前，超完备冗余字典中的原子主要有Gabor、Chirplet、Curvelet、FMmlet、Contourlet、Bandlet、Ricker 子波、正（余）弦、衰减正弦、各向异性精细原子等[14-17]。

2）稀疏分解算法

从稀疏逼近的角度出发，希望在满足一定条件的前提下，从稀疏字典中挑选出分解系数最为稀疏的一组原子，这是一个NP 难问题。目前，主要方法是利用线性规划求解稀疏恢复问题的基追踪算法，具有全局最优优点，但计算复杂度高，且主要适合凸优化问题。另一个主要方法是采用贪婪算法，如匹配追踪算法、框架方法算法、最佳正交基算法、正交匹配追踪算法、分段正交匹配追踪、迭代阀值法、分组匹配追踪算法等[19，20]。由于贪婪算法每一步都要完成信号或残余信号在冗余字典中的每个原子上的投影计算，因此计算量很大[19]。

为了实现贪婪算法的快速计算，相继提出基于原子库结构特性的匹配追踪，由Hilbert 变换确定初始值，以及智能优化算法等[21]。文献[22，23]的研究结果表明，智能优化算法用于稀疏分解，在具有较好精度的同时，还可以降低计算复杂度，节省计算时间。

2.2 观测矩阵

CS 实现的关键是观测矩阵的构造。作为感知的前端，观测系统要求物理上容易实现，并且与表示系统所形成的CS 信息算子稀疏矩阵ψ 具有较小的约束等距常数（RIC）。观测矩阵设计中的两个关键内容就是观测波形和采样方式，设计的主要原则是：（1）观测波形在理论上的最优性能；（2）观测波形的普适性，即要满足和一般的字典或表示系统都具有不相关性；（3）实用性，包括快速计算、低存储量、硬件易实现等。目前常采用的观测矩阵有随机观测、确定性观测和自适应性观测矩阵[24]。

随机矩阵有高斯分布的白噪声矩阵、伯努利分布的±1 矩阵、傅里叶随机矩阵等，它们对大部分信号稀疏矩阵具有非相关性；但是在实际实现中复杂度较高，难以在大规模问题中应用。确定性观测矩阵并不满足普适性，需要基于RIP 理论构造，目前有Chirp 矩阵、Alltop 序列矩阵、半Fourier 矩阵、结构Fourier 矩阵等。文献[24]提出自适应性的观测矩阵，首先产生随机观测矩阵，再利用信号稀疏基的信息，得到优化的观测矩阵；相比随机观测矩阵，优化之后得到的观测矩阵与字典矩阵之间具有更低的相干性。

2.3 信号重构

按优化问题的性质，信号重构可分为：ℓ1-范数下的凸优化、ℓp-范数下的松弛凸优化和ℓ0-范数下的非凸优化。其中，ℓ0-范数是信号重构的本质问题，另两种是为了避免求解非凸优化而提出来的。但是，压缩感知信号重构的ℓ1-范数存在如下问题：（1）它与ℓ0-范数优化解等价性的条件不易判断，并且对一般的实际信号，等价性甚至并不存在；（2）一般情况下，它与真实稀疏解的差距过大，且无法区分稀疏系数的位置；（3）该框架下，对于较长信号，重构的计算复杂度高。ℓp-范数则需要有限等距常数指标，但这是不可计算的，因此在工程应用中欠缺实际意义。ℓ0-范数下的重构，便于引入信号先验，解最稀疏；同时，观测矩阵不再局限于满足特定分布的随机矩阵，具有一致可恢复能力，更适用被噪声污染的实际信号[16]。

目前重构算法主要包括：凸优化方法、贪婪算法和组合算法等[16，17]。凸优化方法包括内点方法、预计梯度法、以及迭代阈值、迭代硬阈值、基于布雷格曼（Bregman）距离的Bregman 迭代等；该方法通过解决一个凸优化问题，用其极小化逼近目标函数，但对于ℓ0-范数下的非凸优化有难度。贪婪算法主要包括匹配追踪及其改进算法，如正交匹配追踪（OMP）、正则化的正交匹配追踪（ROMP）、逐步正交匹配追踪（StOMP）、压缩采样匹配追踪（CoSaMP）、子空间追踪（SP）等；此类算法主要是计算时间长，在有限时间内，解的精度难以保证。组合算法要求对信号高度结构化地采样，经由群测试快速恢复支撑。这类算法包括傅里叶采样、链追踪、HHS 追踪等。此外，已有研究者利用粒子群优化等智能优化算法解决信号重构问题[25]。

3 在电能质量中的应用

在电力系统信号处理领域[7，11，26]，一般将信号分解在一组完备正交基上。这类表示方法试图使用一组固定的基函数来表达任意信号，从而对于一般信号不能总得到信号的简洁表示。为此，Mallat 和Zhang 提出时频原子分解TFAD[27]，将信号在一组过完备的非正交基上分解，从而能根据信号的特点，自适应地选择合适的基来表示信号，分解结果是高度稀疏的，并且能够得到信号的解析表示，成为信号处理领域关注的热点[8]。该方法采用超完备冗余时频原子代替传统的正交基函数，利用原子库的冗余特性捕捉信号的自然特征，可以最佳匹配信号的整体和局部结构，极大地提高了信号表达的简洁性和灵活性[28]，既保持了小波变换的“自适应聚焦”能力，又克服了其在频率域的缺陷，具有良好的抗混叠带通滤波器特性[29]，在信号建模、压缩、特征提取等方面得到广泛应用[8]。

目前，时频原子分解在电能质量中得到了一定应用，包括稀疏分解[8，26，28，30-33]、数据压缩[31，34]和消噪滤波[35]，以及特征选取与分类识别[10，29，36]等。这些应用研究中，采用的原子主要是衰减正弦量原子；此外，文献[36]将电压暂降、电压暂升和电压中断等归为类基波扰动，将电压切痕和电压尖峰扰动归为脉冲扰动，将电压谐波、间谐波、衰减振荡和发散振荡等归为振荡扰动，并根据基波分量和上述3 类扰动的波形结构，分别构建了相应的基波原子库、类基波原子库、脉冲原子库和振荡原子库，为电能质量扰动信号提供了一种很好的尝试，但对于原子匹配优化仍有待进一步研究。关于分解算法，采用最多的还是匹配追踪（MP）算法[8，26，28，30-32，34，35]；此外，还有基于粒子群优化算法的进化匹配方法[33]。

压缩感知理论在电能质量扰动信号中还只是初步应用，涉及压缩采样[6，37]和扰动识别[38]。在压缩采样方面，稀疏基主要采用傅里叶基、小波基和离散余弦变换基；观测矩阵采用变密度采样模板和高斯随机矩阵；信号重构算法为基于TV 最小化共轭梯度法、匹配追踪（MP）、正交匹配追踪（OMP）、逐步正交匹配追踪（StOMP）、GPSR 算法和快速贝叶斯匹配追踪算法等；针对暂态振荡、暂态脉冲、电压凹陷、电压凸起、电压中断、电压波动、电压切痕、电压骤升、电压骤降、短时谐波、间谐波、稳态扰动有谐波，以及多重扰动信号，进行仿真分析，实现了低于Nyquist 采样频率的压缩采样。此外，文献[38]将压缩感知理论引入电能质量扰动模式识别领域，采用高斯分布白噪声生成随机矩阵，提出一种随机降维映射特征提取与稀疏表示分类相结合的电能质量扰动信号识别方法。显然，上述应用仍没有涉及深入的理论分析，包括电能质量扰动信号的稀疏性、稀疏基的适用性、观测矩阵的普适性、非相关性和物理可实现性；同时，重构算法也是基于ℓ1-范数的凸优化算法，并未涉及基于ℓ0-范数的非线性、非凸优化问题。

4 结论

压缩感知理论无疑给电能质量领域带来了新的工具，并且已得到了初步应用。但是，压缩感知应用的前提是信号的稀疏性，同时，只有观测矩阵与稀疏基具有非相关性，才能高概率实现信号重构。然而，目前对于电能质量扰动信号的稀疏性、非相关观测矩阵构造和非线性重构算法，仍有待进一步深入系统研究。

（1）作为压缩感知理论的前提，即：电能质量扰动信号是不是稀疏信号？稀疏度多少？还没有给出明确答案。因此，鉴于电能质量扰动信号的复杂性，稀疏字典的构建、稀疏分解的算法，仍需深入研究。

（2）对于非相关观测矩阵设计，目前主要采用随机观测矩阵，没有结合电能质量扰动信号特点进行优化设计和适用性分析。

（3）现有电能质量压缩感知应用、信号重构都是基于ℓ1-范数下的凸优化，因此，下一步需要开展ℓ0-范数下的信号重构非凸优化算法研究。

（4）对于压缩感知理论，其压缩信息获取的物理实现研究本身仍很不成熟，而且至今未见电能质量扰动信号压缩采样硬件实现的报道，因此，下一步研究重点之一还有基于压缩感知理论的电能质量扰动信号压缩采样，特别是硬件实现，从而成为Nyquist 采样定理的有力补充，实现压缩与采样的同步完成。

（5）基于压缩感知理论的压缩信号处理可以应用于电力系统相关信号的数据压缩与滤波、扰动或故障检测等，仍有待进一步开展研究。

[1]肖湘宁（Xiao Xiangning）. 电能质量科技发展动态及其分析（Development trends of power quality technology and its analysis）[J]. 大功率变流技术（High Power Converter Technology），2010（1）：25-30.

[2]林涛，刘林，曹健，等（Lin Tao，Liu Lin，Cao Jian，et al）.智能电网技术框架下的电能质量监测与分析技术综述（Survey on monitoring and analysis technology of power quality under the smart grid technology framework）[J]. 低压电器（Low Voltage Apparatus），2009（21）：1-6，33.

[3]冯宇，唐轶，石延辉，等（Feng Yu，Tang Yi，Shi Yanhui，et al）. 电能质量分析与参数估计的研究方法综述（Survey on research method of power quality analysis and parameter estimate）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（3）：78-85.

[4]张明， 李开成， 胡益胜 （Zhang Ming，Li Kaicheng，Hu Yisheng）.基于JPEG2000 的电能质量扰动数据压缩方法（Power quality disturbance data compression using JPEG2000）[J]. 电工技术学 报（Transactions of China Electrotechnical Society），2011，26（10）：47-54.

[5]黄南天，徐殿国，刘晓胜，等（Huang Nantian，Xu Dianguo，Liu Xiaosheng，et al）. 基于模式相似性测度的电能质量数据压缩方法（Power quality data compression based on pattern similarity measurement）[J]. 电工技术学报 （Transactions of China Electrotechnical Society），2011，26（10）：39-46，61.

[6]李雪梅，苗桂君，王学伟，等（Li Xuemei，Miao Guijun，Wang Xuewei，et al）. 电能质量信号压缩采样稀疏基性能研究（A research on performance of compression sampling sparse matrix of power quality signal）[J]. 电测 与 仪表（Electrical Measurement & Instrumentation），2011，48（9）：14-17.

[7]Granados-Lieberman D，Romero-Troncoso R J，Osornio-Rios R A，et al. Techniques and methodologies for power quality analysis and disturbances classification in power systems：a review[J].IET Generation，Transmission&Distribution，2011，5（4）：519-529.

[8]贾清泉，于连富，董海艳，等（Jia Qingquan，Yu Lianfu，Dong Haiyan，et al）. 应用原子分解的电能质量扰动信号特征提取方法（Power quality disturbance features extraction based on atomic decomposition）[J]. 电力系统自动 化（Automation of Electric Power Systems），2009，33（24）：61-64，93.

[9]苏玉香，刘志刚，李科亮，等（Su Yuxiang，Liu Zhigang，Li Keliang，et al）. Hilbert-Huang 变换在电气化铁路谐波检测中的应用（Application of Hilbert-Huang transform in harmonic detection of electrified railway）[J]. 电网技术（Power System Technology），2008，32（18）：30-35.

[10]曹健，林涛，徐遐龄，等（Cao Jian，Lin Tao，Xu Xialing，et al）. 一种电能质量扰动监测与识别新方法 （A new method for measurement and classification of power quality disturbance）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，31（31）：125-133.

[11]刘林，林涛，徐遐龄，等（Liu Lin，Lin Tao，Xu Xialing，et al）. 应用于低频振荡在线监测的并行时频原子复带通滤波方法（Concurrent time-frequency atom complex band-pass filter based method for online monitoring lowfrequency oscillation）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，31（25）：58-65.

[12]Eldar Y C，Kutyniok G. Compressed Sensing：Theory and Applications[M].Cambridge：Cambridge University Press，2012.

[13]Candes E J，Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine，2008，25（2）：21-30.

[14]石光明，刘丹华，高大化，等（Shi Guangming，Liu Danhua，Gao Dahua，et al）. 压缩感知理论及其研究进展（Advances in theory and application of compressed sensing）[J].电子学报（Acta Electronica Sinica），2009，37（5）：1070-1081.

[15]戴琼海，付长军，季向阳（Dai Qionghai，Fu Changjun，Ji Xiangyang）. 压缩感知研究（Research on compressed sensing）[J]. 计算机学报（Chinese Journal of Computers），2011，34（3）：425-434.

[16]焦李成，杨淑媛，刘 芳，等（Jiao Licheng，Yang Shuyuan，Liu Fang，et al）. 压缩感知回顾与展望（Development and prospect of compressive sensing）[J]. 电子学报（Acta Electronica Sinica），2011，39（7）：1651-1662.

[17]杨海蓉，张 成，丁大为，等（Yang Hairong，Zhang Cheng，Ding Dawei，et al）. 压缩传感理论与重构算法（The theory of compressed sensing and reconstruction algorithm）[J]. 电 子 学 报（Acta Electronica Sinica），2011，39（1）：142-148.

[18]Davenport M A，Boufounos P T，Wakin M B，et al. Signal processing with compressive measurements[J].IEEE Journal of?Selected Topics in Signal Processing，2010，4（2）：445-460.

[19]刘丹华，石光明，周佳社（Liu Danhua，Shi Guangming，Zhou Jiashe）. 一种冗余字典下的信号稀疏分解新方法（New method for signal sparse decomposition over a redundant dictionary）[J]. 西安电子科技大学学报（Journal of Xidian University），2008，35（2）：228-232.

[20]Blumensath T，Davies M E. Normalized iterative hard thresholding：Guaranteed stability and performance [J].IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：298-309.

[21]陈发宇，尚永生，杨长春（Chen Fayu，Shang Yongsheng，Yang Changchun）.Matching Pursuits 方法综述 （A general description of matching pursuits decomposition method）[J]. 地球物理学进展（Progress in Geophysics），2007，22（5）：1466-1473.

[22]李亚文，于凤芹（Li Yawen，Yu Fengqin）. 一种改进选择算子的遗传匹配追踪算法（Genetic matching pursuit algorithm with improved selection operators）[J]. 数 据 采 集与处理（Journal of Data Acquisition&Processing），2011，26（2）：177-180.

[23]王春光，刘金江，孙即祥（Wang Chunguang，Liu Jinjiang，Sun Jixiang）. 基于粒子群优化的稀疏分解最优匹配原子搜索算法（Algorithm of searching for the best matching atoms based on particle swarm optimization in sparse decomposition）[J]. 国防科技大学学报（Journal of National University of Defense Technology），2008，30（2）：83-87.

[24]Duarte-Carvajalino J M，Sapiro G.Learning to sense sparse signals：simultaneous sensing matrix and sparsifying dictionary optimization[J]. IEEE Trans on Image Processing，2009，18（7）：l395-1408.

[25]Benjamin D V R.Image Compression and Recovery Using Compressed Sampling and Particle Swarm Optimization[D].Texas：Baylor University，2009.

[26]贾清泉， 于连富， 王宁， 等 （Jia Qingquan，Yu Lianfu，Wang Ning，et al）. 原子稀疏分解算法在电力系统扰动信号分析中的应用（Application of atomic sparse decomposition to power systems disturbance analysis）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（19）：17-21.

[27]Mallat S G，Zhang Zhifeng. Matching pursuits with timefrequency dictionaries[J]. IEEE Trans on Signal Processing，1993，41（12）：3397-3415.

[28]李 明，张 葛 祥，王 晓 茹（Li Ming，Zhang Gexiang，Wang Xiaoru）. 时频原子方法在间谐波分析中的应用（Application of time-frequency atom method in inter-harmonics analysis）[J].电网技术（Power System Technology），2009，33（17）：81-85.

[29]曹健，林涛，徐遐龄，等（Cao Jian，Lin Tao，Xu Xialing，et al）. 基于最小二乘法和时频原子变换的谐波/间谐波测量算法 （Monitoring of power system harmonic/inter-harmonics based on least squares algorithm and time frequency transform）[J]. 电工技术学报 （Transactions of China Electrotechnical Society），2011，26（10）：1-7.

[30]Lovisolo L，da Silva E A B，Rodrigues M A M，et al. Efficient coherent adaptive representation of monitored electric signals in power systems using damped sinusoids[J].IEEE Trans on Signal Processing，2005，53 （10）：3831-3846.

[31]Tcheou M P，Lovisolo L ，da Silva E A B，et al. Optimum rate-distortion dictionary selection for compression of atomic decompositions of electric disturbance signals [J]. IEEE Signals Processing Letters，2007，14（2）：81-84.

[32]李明，王晓茹（Li Ming，Wang Xiaoru）. 采用时频原子方法的电压闪变检测（Detection of voltage flicker based on time-frequency atom method）[J]. 电网技术 （Power System Technology），2010，34（7）：94-97.

[33]Yang Qing，Wang Jing，Sima W，et al. Mixed over-voltage decomposition using atomic decompositions based on a damped sinusoids atom dictionary[J]. Energies，2011，4（9）：1410-1427.

[34]Lovisolo L，da Silva E A B，Rodrigues M A M，et al. Efficient coherent adaptive representations of monitored electric signals in power systems using damped sinusoids[J].IEEE Trans on Signal Processing，2005，53（10）：3831-3846.

[35]Lovisolo L，Tcheou M P，da Silva E A B，et al.Modeling of electric disturbance signals using damped sinusoids via atomic decompositions and its applications[J]. Eurasip Journal on Advances in Signal Processing，2007， 2007（1）：1-15.

[36]王宁，李林川，贾清泉，等（Wang Ning，Li Linchuan，Jia Qingquan，et al）. 应用原子分解的电能质量扰动信号分类方法（Classification of power quality disturbance signals using atomic decomposition method）[J]. 中国电机工程学报（Proceedings of the CSEE），2011，31（4）：51-58.

[37]苗桂君，王学伟，杨立国，等（Miao Guijun，Wang Xuewei，Yang Liguo，et al）. 短时电能质量信号压缩采样方法的研究（Research on compression sampling algorithm of short-time power quality）[J]. 电 测 与 仪 表（Electrical Measurement&Instrumentation），2010，47（12）：8-11，19.

[38]沈跃，刘国海，刘慧（Shen Yue，Liu Guohai，Liu Hui）. 随机降维映射稀疏表示的电能质量扰动多分类研究（Study on classification method of power quality disturbances based on random dimensionality reduction projection and sparse representation）[J]. 仪器仪表学报（Chinese Journal of Scientific Instrument），2011，32 （6）：1371-1376.