MUSIC 和Prony 在电动机断条故障检测中的应用

朱天敬，许伯强

（华北电力大学电气与电子工程学院，保定071003）

异步电动机的故障类型很多，检测方法各异[1，2]。其中，转子断条故障是鼠笼型异步电动机的常见故障之一，占电动机故障的10%左右，因此，对异步电动机转子断条故障进行检测以便实施可靠诊断有着重要的研究价值。

当笼型异步电动机出现断条故障时，其定子电流中将出现（1±2 s）f1频率的电流分量[3，4]，其中s 为转差率，f1为工频。该电流分量称为边频分量，可视为断条故障的特征。由此，可通过对定子电流信号进行傅里叶频谱分析来检测转子断条故障[5]。但是，由于（1±2 s）f1分量的幅值很小，与f1分量的幅值之比值约为0.01～0.03；并且异步电动机运行时的转差率s 很小，使两者频率在数值上非常接近，若用快速傅里叶变换FFT（fast Fourier transform）直接对定子电流信号做频谱分析，（1±2 s）f1频率分量会被基波f1频率分量的泄漏所淹没，使得（1±2 s）f1频率分量的存在与否无法准确判断。为克服上述困难，文献[6]通过对异步电动机启动电流的时变频谱分析，使得算法对频率分辨力的要求大大降低，在一定程度上克服了稳态运行时FFT 分析的不足，但需在电机启动时才能检测，无法对运行的电机实时监测，有一定的局限性；文献[7]利用自适应滤波技术对定子电流进行处理，抵消其中的f1频率分量，然后再进行FFT 分析，从而突出了（1±2 s）f1频率分量，提高了故障检测的灵敏度与可靠性；文献[8-10]对异步电动机瞬时功率信号、瞬时相位角信号进行FFT 分析，用来监测异步电动机转子故障。但均需要足够的采样点数，即连续采集足够时长的定子电流信号才能保证频率高分辨力，以切实分辨出转子断条故障特征。另外，傅里叶频谱分析结果的准确性在一定程度上依赖于待处理信号在采样时段内的平稳性。但是，在工程实际中，一定程度的负荷波动、噪声等是不可避免的，信号采样时间过长往往意味着引入这些干扰而影响傅里叶频谱分析结果的准确性，并恶化转子断条故障检测性能。文献[11]对此做了具体分析、说明。解决上述问题的关键在于：在保证高频率分辨力的前提下，针对采样时长尽可能短的定子电流信号实施转子断条故障检测。

多重信号分类技术MUSIC（multiple signal classification）的基本思想是通过对信号的自相关矩阵进行特征值分解，将信号的特征空间分解为同信号分量相对应的信号子空间以及同信号分量相正交的的噪声子空间，利用信号子空间与噪声子空间的正交性来估计信号频率。该方法在理论上具有任意高的频率分辨力，从这个意义上讲，MUSIC 算法具有傅里叶变换法无可比拟的优越性。加之该算法自身具备抑制噪声的能力，因此非常适用于笼型异步电动机转子断条故障的检测。

文献[12-15]对MUSIC 算法在异步电动机转子断条故障检测领域进行了初步探讨，结果表明：即使对于短时信号，MUSIC 依然可以准确估计出定子电流信号中各个分量的频率，但却无法估计出各频率分量的幅值，而各频率的幅值对于判定转子断条故障的严重程度至关重要[16]。

本文引入扩展Prony 算法来确定定子电流信号中各个分量的幅值、初相角，对于仿真信号，效果理想。进而对一台Y100L-2 型3 kW 笼型异步电动机完成了相关物理实验。实验结果表明：基于实值Root_MUSIC 和扩展Prony 算法异步电动机转子断条故障检测方法是行之有效的，并且由于仅需对短时信号进行分析处理而优于以往方法。

1 基于实值Root_MUSIC 的频率估计

实际检测到的异步电动机故障信号为实周期信号，并且满足狄里赫利条件，即

式中：x（n）为采样信号；n 为采样点数；Ts为采样周期；p 为谐波个数；fi为第i 次谐波分量的频率；Ai、φi分别为第i 次谐波分量的幅值和初始相位；v（n）为零均值且方差为σ2的高斯白噪声。

定义一个长度为m 的观察矢量矩阵为

一般取m〉2p，则N 点采样数据构成的矩阵为

由于该模型均为实值数据，因此较之于传统复域类的Root_MUSIC 模型数据少[17]。

根据Root_MUSIC 频谱估计原理可得矢量矩阵X 的自相关矩阵为

式中，E为数学期望。对Rxx自相关矩阵Rxx进行特征值分解，可得

其中：

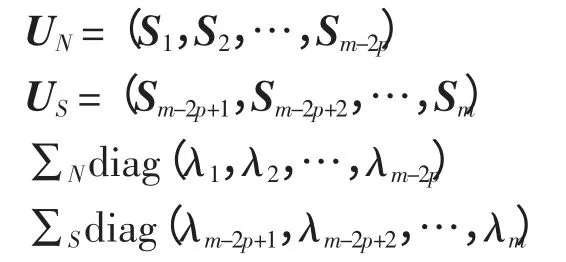
式中：λl和Sl分别为Rxx第l 个特征值及其对应的特征矢量，且λ1≈λ2≈…≈λm-2p≤λm-2p+1≤…≤λm，可根据特征值大小判断信号源的个数为p；UN为Rxx的前m-2p 个小特征值对应的特征矢量张成的子空间，称之为噪声子空间；US为Rxx的后2p 个小特征值对应的特征矢量张成的子空间，称之为噪声子空间。则根据Pisarenko 谐波分解的思想，给出空间频率的估计，即

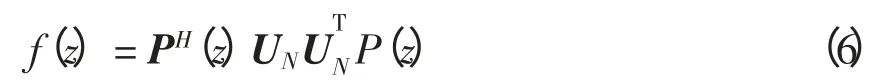
其中：P（z）=[1，z，…，zm-1]T；上标H 表示共轭转置。

实际实验中采集的信号为实正弦信号，1 个实正弦信号可以表示成2 个复正弦信号的和或差，得到的频率为正负2 个对称的频率，阶次为相应的复正弦阶次的2 倍。

2 基于扩展Prony 算法的幅值和相角估计

Prony 算法是使用指数函数的线性组合来描述等间距采样的数学模型[18，19]。经过适当的扩展后，Prony 方法可用来估计有理式功率谱密度[17]。扩展Prony 方法采用的数学模型为一组p 个具有任意幅值、相位、频率与衰减因子的指数函数，令衰减因子α=0，则其离散时间的函数为

利用Root_MUSIC 算法求出异步电动机转子断条故障特征分量及其他分量的频率值之后，指数信号个数M 和Prony 极点zi就成了已知量。此时M=2p，令

式中，N 为数据x（n）的长度。则指数模型可表示为

由总体最小二乘估计可得

由于噪声信号的幅值较小，因此，可用测量信号xn来代替实际信号中未知的n。则信号的中各频率分量的幅值和相位分别为

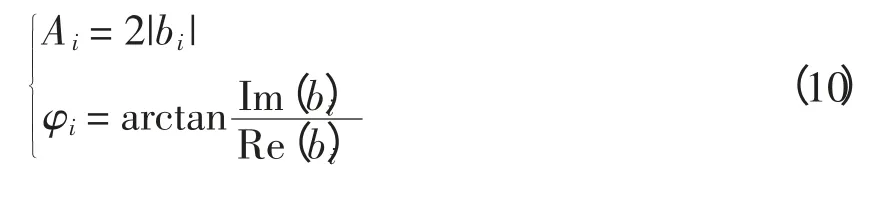
3 仿真信号分析

将分析Root_MUSIC 与扩展Prony 方法应用于转子断条故障检测的研究，仿真结果见表1。异步电动机发生转子断条故障后，定子电流信号为

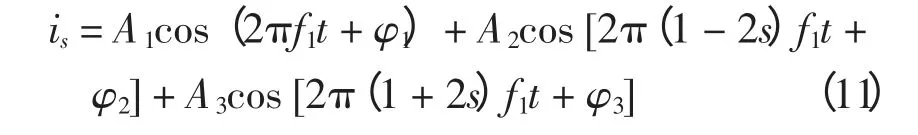
式中：s 为转差率，s=0.2%，体现工程实际中转差率甚低的情况；取Ts=0.001 s、N=1 000、f1=50 Hz。

表1 Root_MUSIC 与扩展Prony 算法的计算结果Tab.1 Result of Root_MUSIC and expansion Prony algorithm

由表1 中的数据表明，对于短时间采样信号，Root_MUSIC 与扩展Prony 算法可以准确地计算出信号中各分量的频率、幅值和初相角。随机变换s、f1、A1、φ1、A2和φ2的取值，并进行大量的计算，结果均相符。据此，将该方法应用于异步电动机转子断条故障检测具备可行性。由于该方法仅需短时采样信号，亦适用于负荷波动、噪声等不利的情况。

4 实际异步电动机转子断条故障检测

实验电机为1 台Y100L-2 型、3 kW、380 V、6.12 A、50 Hz 的三相异步电动机，如图1 所示。除正常转子外，还配备了一个故障转子来模拟断条故障，该故障转子存在一根断裂的导条（距离端环10 mm 处钻孔、孔深度10 mm、孔直径6 mm）。实验接线如图2 所示。

4.1 实验电机满载

图1 实验设备Fig.1 Experimental rig

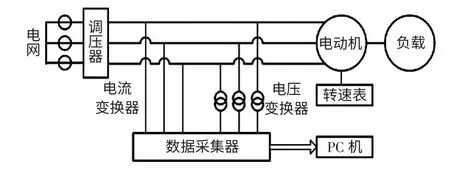
图2 实验接线Fig.2 Experimental system scheme

在实验电机满载（s = 3.6%）且转子断条情况下，采集定子电流a 相信号，分别取15 s 数据进行自适应滤波细化FFT 分析[7，20]、取1.5 s 数据进行自适应滤波细化FFT 分析、取1.5 s 数据进行Root_MUSIC-扩展Prony 分析，其图形如图3 所示，具体实验数据见表2。

图3 电机满载情况下的实验结果Fig.3 Experimental results under condition of fully loaded motor

由图3 及表2 可知：实验电机满载时，基于Root_MUSIC 和扩展Prony 算法的异步电动机转子断条故障是可行的，且由于仅需1.5 s 的短时数据即可保证检测可靠性，优于以往方法。

表2 电机满载情况下的实验结果Tab.2 Experimental results under the condition that the

4.2 实验电机半载

在实验电机半载（s=1.8%）转子断条情况下，采集定子电流a 相信号，分别取15 s 数据进行自适应细化FFT 分析，取1.5 s 数据进行自适应细化FFT 分析，取1.5 s 数据进行Root_MUSIC-扩展Prony 分析频，其图形如图4 所示，具体实验数据见表3。

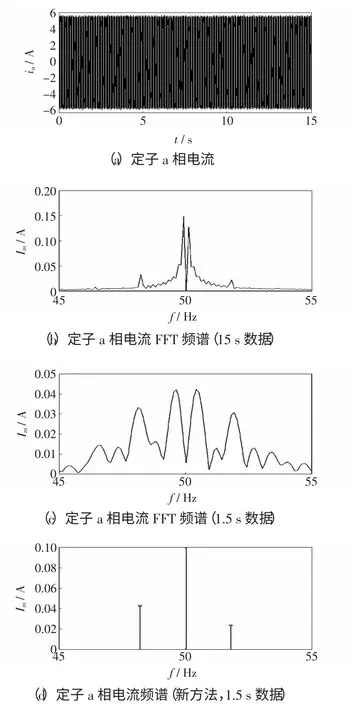
图4 电机半载情况下的实验结果Fig.4 Experimental results under the condition of motor half-loaded

由图4 及表3 可知：实验电机半载时，取15 s数据进行自适应滤波细化FFT 分析与取1.5 s 数据进行Root_MUSIC-扩展Prony 分析结果互相吻合；但取1.5 s 数据进行自适应滤波细化FFT 分析却得到了偏差较大的结果，其确定的边频分量的频率值与（1±2 s）f1、s、f1在数值上已经失去了匹配关系。

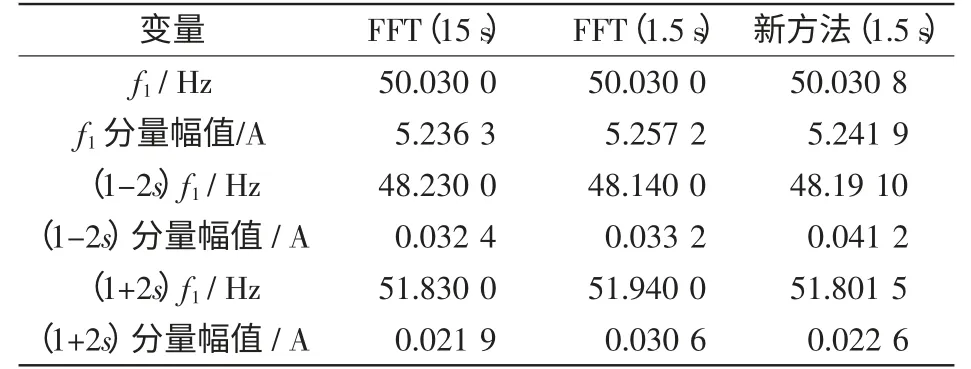
表3 电机半载情况下的实验结果Tab.3 Experimental results under condition of half-loaded motor

上述实验结果进一步表明，基于Root_MUSIC与扩展Prony 算法的转子断条故障检测方法是可行的，且由于仅需短时数据（1.5 s）即可保证对转子断条故障检测的性能，可推断其适用于负荷波动、噪声干扰等不利情况。

5 结论

（1）以仿真信号模拟转子断条故障信号检验实值Root_MUSIC 的结果说明：Root_MUSIC 算法对短时信号亦具有高频率分辨力，但却无法给出各频率分量的幅值及相角。

（2）引入扩展Prony 算法计算各频率分量的幅值、初相角，效果理想，形成了基于实值Root_MUSIC和扩展Prony 算法的笼型异步电动机转子断条故障检测方法。

（3）对1 台Y100L-2 型3 kW 的笼型异步电动机进行了转子断条故障实验。实验结果表明：基于实值Root_MUSIC 和扩展Prony 算法的笼型异步电动机转子断条故障检测方法具备可行性，且由于仅需对短时采样信号进行处理而适用于负荷波动、噪声干扰等不利情况。

[1]韩天， 尹忠俊， 杨邵伟 （Han Tian，Yin Zhongjun，Yang Shaowei）. 电机转子断条故障诊断方法探讨（Discussion of diagnostic methods for broken rotor bar of induction motor）[J]. 电力系统及其自动化学报 （Proceedings of the CSU-EPSA），2009，21（1）：93-98，117.

[2]达夫勒P J，彭曼J. 电机的状态监测[M]. 北京：水利电力出版社，1992.

[3]Deleroi W. Broken bar in squirrel-cage rotor of an induction motor-part 1：description by superimposed fault-currents[J]. Archiv fur Elektrotechnik Berlin，1984，67（2）：91-99.

[4]马宏忠，胡虔生，黄允凯，等（Ma Hongzhong，Hu Qiansheng，Huang Yunkai，et al）. 感应电机转子绕组故障仿真与实验研究（Simulating and experiment studying on rotor winding fault of induction motor）[J]. 中国电机工程学报（Proceedings of the CSEE），2003，23（4）：107-112.

[5]董爱华，付子义，康润生，等（Dong Aihua，Fu Ziyi，Kang Runsheng，et al）. 频谱分析及其在异步电动机转子断条诊断方面的应用 （Frequency analysis and its application in the diagnosis for the open circuit rotor of asynchronous motor）[J]. 焦作工学院学报（Journal of Jiaozuo Institute of Technology），1998，17（1）：71-74.

[6]邱阿瑞（Qiu Arui）. 用起动电流的时变频谱诊断鼠笼异步电机转子故障（Diagnosis of rotor fault in squirrel-cage induction motors using time-varying frequency spectrum of starting stator current）[J]. 中国电机工程学报（Proceedings of the CSEE），1995，15（4）：267-273.

[7]姜建国，汪庆生，杨秉寿，等（Jiang Jianguo，Wang Qingsheng，Yang Bingshou，et al）. 用自适应方法提取鼠笼式异步电机转子断条的特征分量（Applying the adaptive noise cancellation to extract the features of squirrel cage induction motor with rotor defects）[J]. 电 工 技 术 学 报（Transactions of China Electrotechnical Society），1990，5（4）：1-6.

[8]Liu Zhenxing，Yin Xianggen，Zhang Zhe，et al. Online rotor mixed fault diagnosis way based on spectrum analysis of instantaneous power in squirrel cage induction motors[J].IEEE Trans on Energy Conversion，2004，19（3）：485-490.

[9]Drif M，Cardoso A J M.The use of the instantaneous-reactive-power signature analysis for rotor-cage-fault diagnostics in three-phase induction motors [J]. IEEE Trans on Industrial Electronics，2009，56（11）：4606-4614.

[10]Drif M，Cardoso A J M. Rotor cage fault diagnostics in three-phase induction motors，by the instantaneous phaseangle signature analysis [C]//IEEE International Symposium on Industrial Electronics.Antalya，Turkey：2007.

[11]Aboubou A，Sahraoui M，Zouou S E，et al. Broken bars and/or end rings detection in three-phase induction motors by the extended Park′s vector approach[C]//9th IEEE International Power Electronics Congress. Celaya，Mexico：2004.

[12]Pereira L A，Fernandes D，Gazzana D S，et al. Application of the Welch，Burg and MUSIC methods to the detection of rotor cage faults of induction motors[C]//IEEE/PES Transmission&Distribution Conference&Exposition.Caracas，Venezuela：2006.

[13]Kia S H，Henao H，Capolino G A. A high-resolution frequency estimation method for three-phase induction machine fault detection[J]. IEEE Trans on Industrial Electronics，2007，54（4）：2305-2314.

[14]方 芳，杨士元，侯新国（Fang Fang，Yang Shiyuan，Hou Xinguo）. 基于改进多信号分类法的异步电机转子故障特征分量的提取（Rotor fault feature extraction of motor faults of induction motor based on a modified music method）[J]. 中国电机工程学报（Proceedings of the CSEE），2007，27（30）：72-76.

[15]许伯强，孙丽玲，李和明（Xu Boqiang，Sun Liling，Li Heming）. 基于多重信号分类与模式搜索算法的笼型异步电动机转子断条故障检测新方法（A detection method for broken rotor bar fault in induction motors based on multiple signal classification and pattern search algorithm）[J]. 中国电机工程学报（Proceedings of the CSEE），2012，32（9）：93-99.

[16]许伯强，孙丽玲，李和明（Xu Boqiang，Sun Liling，Li Heming）. 笼型异步电动机转子断条数目诊断新判据（A novel diagnosis criterion for broken rotor bars in induction motors）[J]. 中国电机工程学报（Proceedings of the CSEE），2009，29（6）：105-110.

[17]张贤达.现代信号处理[M].北京：清华大学出版社，2002.

[18]丁屹峰，程浩忠，吕干云，等（Ding Yifeng，Cheng Haozhong，Lü Ganyun，et al）. 基于Prony 算法的谐波和间谐波频谱估计（Spectrum estimation of harmonics and interharmonics based on Prony algorithm）[J]. 电工技术学报（Transactions of China Electrotechnical Society），2005，20（10）：94-97.

[19]Kay S M，Marple S L Jr. Spectrum analysis—a modern perspective[J]. Proceedings of the IEEE，1981，69（11）：1380-1419.

[20]许伯强，李和明，孙丽玲，等（Xu Boqiang，Li Heming，Sun Liling，et al）. 笼型异步电动机转子断条故障检测新方法（A novel detection method for broken rotor bars in induction motors）[J]. 中国电机工程学报（Proceedings of the CSEE），2004，24（5）：115-119.