Duffing系统中微弱信号起始点的检测

苗长云，王有玺，高 华，苗春浇

（1.天津工业大学电子与信息工程学院，天津 300387；2.北京交通大学电子信息工程学院，北京 100044）

Duffing系统中微弱信号起始点的检测

苗长云1，王有玺1，高 华1，苗春浇2

（1.天津工业大学电子与信息工程学院，天津 300387；2.北京交通大学电子信息工程学院，北京 100044）

为从时域上检测微弱信号在系统中出现的时间点，提出了一种基于Duffing系统的微弱信号起始点的间接检测方法.首先将微弱信号与Duffing系统自身的信号相叠加，混合测量后剔除其中Duffing系统产生的信号，再利用dmey小波对待测信号加入系统造成的轨道偏离过程进行时域分析，可较准确测出微弱信号的起始点.由于混沌系统本身对高斯噪声的自免疫特性，因此本方法具有一定的抗噪性.仿真结果显示：该方法能有效地从时域上检测到微弱信号的起始点，其相对误差可达到10-3s，可应用于心动信号特征参数的提取.

Duffing系统；微弱信号；起始点检测；dmey小波分析

近年来，微弱信号的检测已在很多领域大量应用.目前，采用Duffing振子利用混沌、大尺度周期的相态变化对驱动信号幅值的敏感性进行微弱信号的检测已成为研究的热点[1-4].周玲等[5]采用Duffing混沌振子系统,通过判断相轨迹的状态变化对微弱信号进行检测研究.Wang等[6]提出了一种利用谐振与混沌之间过渡检测微弱信号的方法，并且利用Melnikov的方法确定了混沌的阈值，该方法是从频域上展开分析的.Liu等[7]等阐述微弱信号在高斯白噪声的影响下引起系统由混沌态进入大尺度周期态的过程，改进了检测系统降低信噪比的方法，研究了噪声对Lyapunov指数的影响.但是以往采用Duffing系统对微弱信号检测的研究重点放在混周渐变的状态变化上，利用混周渐变的状态变化实现对微弱信号的检测.一方面，由于混周渐变的阈值无法准确求出，目前只能求得近似值，对测量精度有一定的影响；另一方面，缺少从时域上对暂态微弱信号的变化过程进行分析.实际上，采用Duffing振子的微弱信号检测，不应仅局限于对系统的状态变化进行分析，还需要在时域上对微弱信号加入系统后系统的轨道偏离过程进行分析，以准确判断出待检测信号在系统中出现的时间点.本文提出了一种基于Duffing系统的微弱信号起始点检测方法.采用间接测量的方法，将微弱信号与Duffing系统产生的信号相叠加，混合测量后剔除其中Duffing系统产生的信号，再利用dmey小波对待测信号加入系统造成的轨道偏离过程进行时域分析，由于混沌系统本身对高斯噪声的自免疫特性，因此本方法具有一定的抗噪性，能够准确检测出微弱信号的起始点，这对于心动信号特征参数的提取[8-9]具有重要意义.

1 检测原理

Duffing振子方程为

式中：（-x+x3）为非线性系统恢复力项；k为系统阻尼比；γ为周期策动力的幅值；ω为策动力的角频率.

一般来说，在系统的阻尼比k和策动力的角频率ω一定的条件下，系统的状态会随着周期策动力γ的幅值变化而变化[10].随着γ的逐渐增大，系统会出现有规律的变化，要历经同宿轨道、分叉轨道、混沌轨道、临界周期状态和大尺度周期状态等.

当γ0＜γd（系统由混沌态跃迁至大尺度周期态的临界阈值）时，系统会处于混沌态，其相态表现出无穷嵌套自相似结构和内在的随机性，每一时刻所处的状态和位置均不相同.

当输入信号掺杂高斯白噪声的干扰时，由于混沌系统本身具有一定的抗噪能力，得到的相态图会变成具有一定锯齿状的混沌态，但其状态并未发生变化.

本文利用系统的混沌态对微弱信号进行检测，其检测系统的方程为

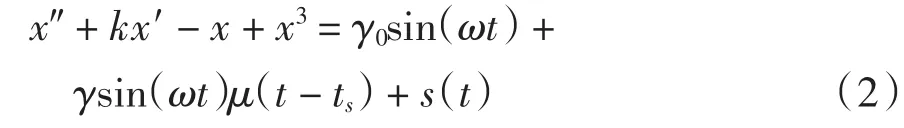
式中：γsin（ωt）为待检测微弱信号；μ（t-ts）为阶跃信号，使待检测微弱信号在t=ts时刻加入系统；s（t）为高斯白噪声.检测原理如下：调整系统的驱动幅值γ0，使得系统处于混沌态，在不加入待测微弱信号的情况下，对系统（1）进行仿真，得到相平面的轨迹（x1（t），y1（t））；固定驱动幅值γ0，加入待测微弱信号γsin（ωt）μ（t-ts），再次对系统（1）进行仿真，再次得到相平面的轨迹（x2（t），y2（t））.由Duffing方程的性质可知，该信号的加入，不一定会改变系统（1）所处的相态，但会在该信号加载的时刻起，使相平面的轨道偏离原有轨迹，即Δx=|x2-x1|＞0，Δy=|y2-y1|＞0.检测该轨迹的偏移值，利用dmey小波[11]对Δx、Δy信号进行时域分析，可准确得出待检测信号的起始点.

本文采用四阶R-K来分析加入待测信号前后的Duffing方程轨迹的偏离值.

当没有待检测信号γ0sin（ωt）时，系统的方程如式（1）所示，令y=x′，则方程可转化为

采用四阶的R-K法进行分析，设f（t，x，y）=x′，g（t，x，y）=y′，则方程转化为

将（4）式代入（5）式化简，由于采用RK的步长较小，可约去步长h的高阶小量，可得

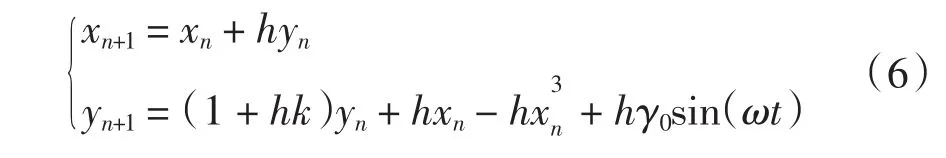
当存在待检测信号γsin（ωt）时，则（3）式变为

同理采用四阶RK法可得

由（2）式中μ（t-ts）为阶跃函数，则可以设阶跃信号在ts时刻加入系统，即当t=ts时刻待检测信号γsin（ωt）开始加入系统，满足

如果在t=ts+1时刻待测信号未加入系统，则满足（6）式，即

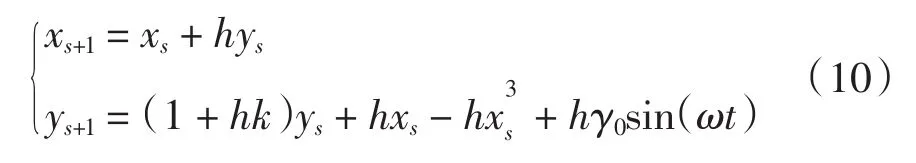
当t=ts+1时，阶跃信号μ（t-ts）=1，待检测信号加入系统，则满足（8）式，即

将（11）式与（10）式相减，可得待测信号对系统造成的轨迹偏离

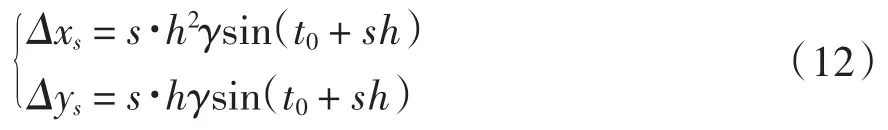
由（12）式可知，因Δxs中含有h的高阶项，利用时域分析方法对Δys进行分析会比较容易获取起始点值.

因此，本文利用dmey小波对Δys进行时域分析，以获取系统轨道偏离的起始位置，进而实现对待检测信号的起始点进行检测.

文中采用dmey小波即meyer小波[12-13]的表达式为

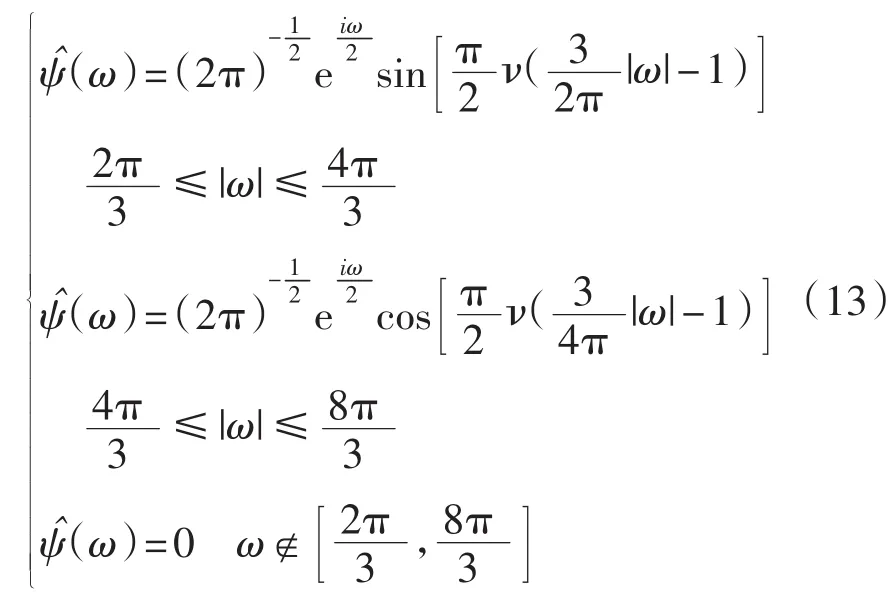
其中ν（a）函数的表达式为

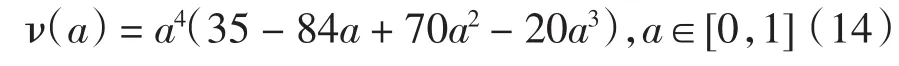
因文中采用的ω=10 rad/s值并不在上述范围内，故要让跳变点出现在第一层的话，需要对（ω）函数进行平移[14].对ω向右平移2π后可符合（13）式中的第1式，则第1式可变为

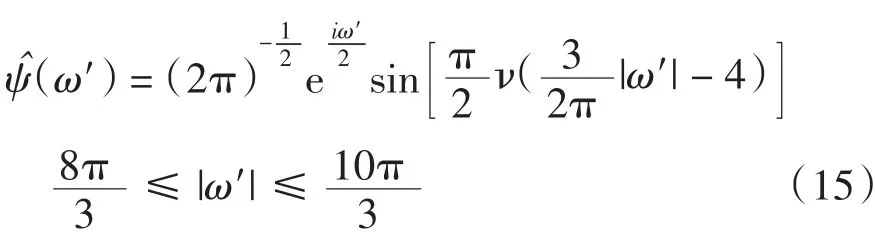
则相应的ν（a′）可变为

联合（15）式和（16）式，将 ω=10 rad/s代入，可得（10）=26.198 14ei.当ω的取值不在（15）式范围内时，例如ω=1 rad/s时，（1）=0，因此利用meyer小波对此进行时域分析会得到较好的阶跃现象，容易获取跳频点.

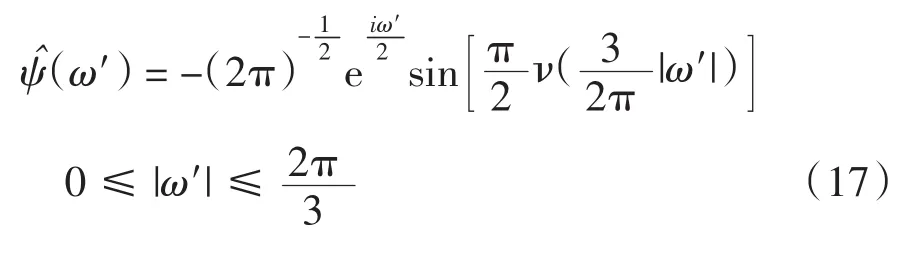
则相应的ν（a′）可变为

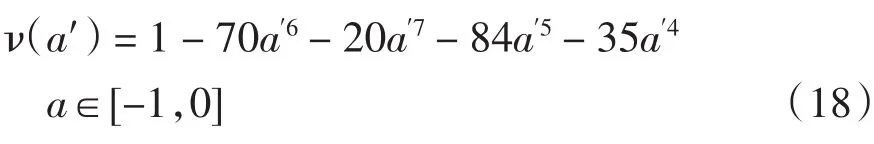
2 仿真分析

按照方程（1）建立混沌态微弱信号测量系统，为确保系统处于混沌态，就要先确定系统的阈值γd[15].利用melnikov的定义对（3）式进行分析，可得γ0的下限为γ0＞0.376 5，利用相态图进行实验估计，可得出其阈值上限γd在0.725 616 119 2～0.725 616 119 3之间，即当0.725 6＞γ0＞0.376 5时，系统将处于混沌态，故仿真中可令γ0=0.625 5＜γd.

当k=0.5，ω=10 rad/s时，仿真得到相应的数据，利用MATLAB分别保存此状态下不同时刻各信号的位置，记为x1，y1.

设待检测微弱信号和高斯白噪声的混合信号在ts=37 s时加入，再次仿真，保存此状态下的不同时刻信号的位置，记为x2，y2.然后分别求得两组信号的差值Δx=|x2-x1|，Δy=|y2-y1|，其时域图如图1所示，由图中可以准确得到待检测微弱信号的存在.

图1 待检测信号加入系统后轨道前后的偏离时域图Fig.1 Time domain chart of track deviation as signal to be adding into system

再利用dmey小波对信号的差值进行时域分析，如图2（a）所示，可以清晰地看到在某时刻信号的Δy发生跳跃，将变化点图像放大得到图2（b），读取数值可知，信号在ts=37.001 s时加入系统，这与初始设定值基本吻合.

同理，令ω分别取值10、7、1 rad/s时，当ts=21、15、9 s时进行实验仿真，得到的实验数据如表1所示.

由表1可以看出，采用dmey小波分解方式进行时域分析，能比较准确地测量出待检测信号的起始点.测量精度在实验中能到达毫秒级别，实验误差较小，证实了本文方法的有效性.

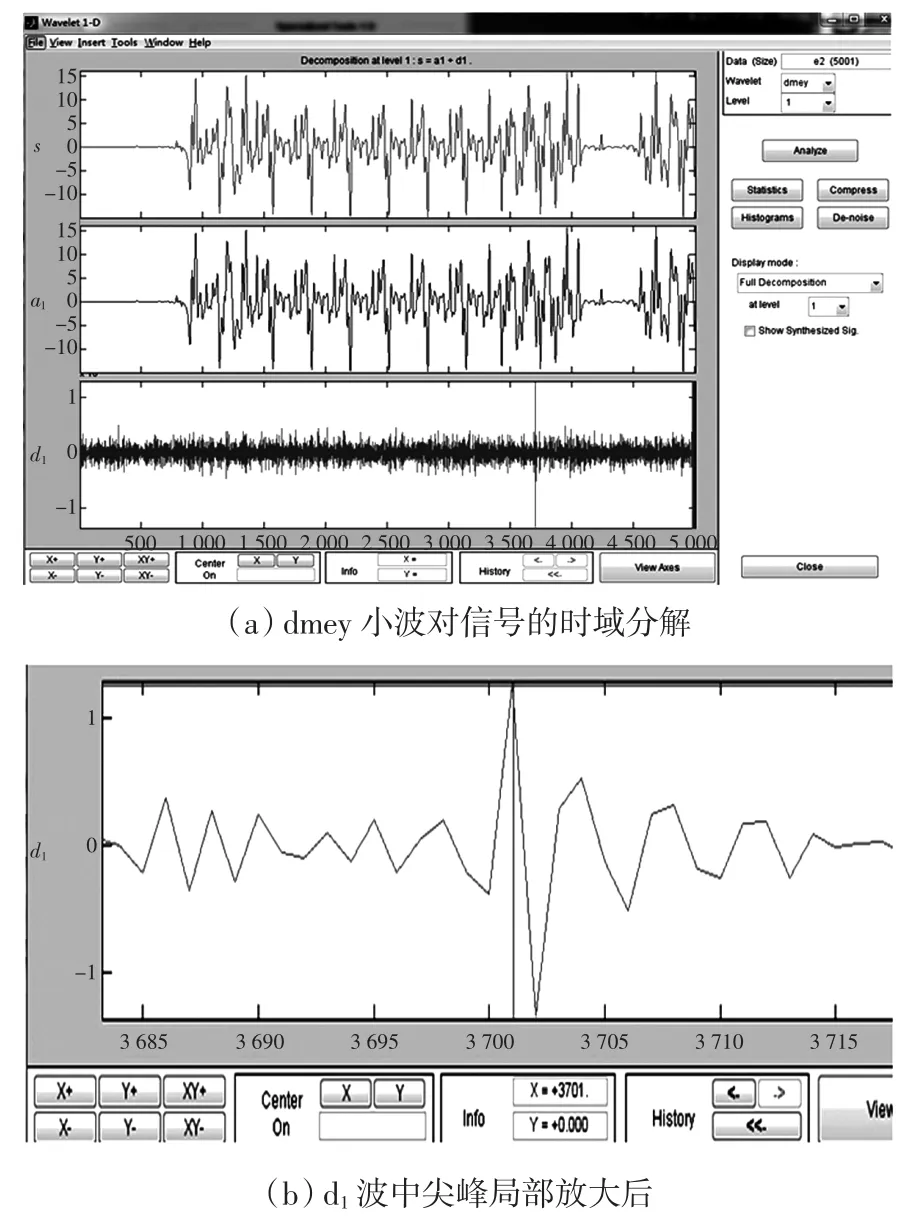
图2 经dmey小波分析后的时域图Fig.2 Time domain chart after dmey wavelet analysis

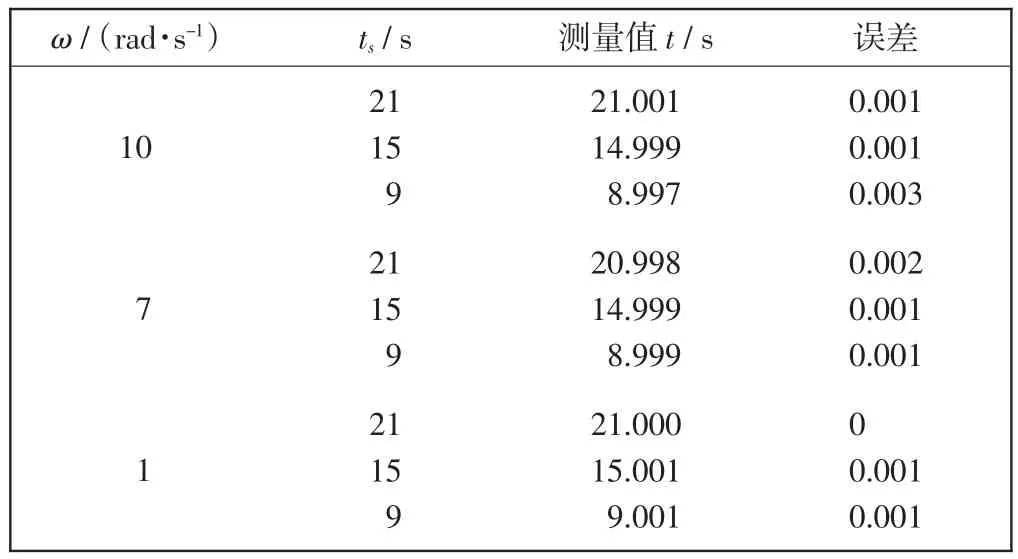
表1 dmey小波分析结果Tab.1 Results of dmey wavelet analysis

3 结束语

本文提出了基于Duffing系统的微弱信号起始点检测方法.由于微弱信号本身不易被直接测量，故采用间接测量的方法，首先将微弱信号与Duffing系统自身的信号相叠加，混合测量后剔除其中Duffing系统产生的信号，再利用dmey小波对待测信号加入系统造成的轨道偏离过程进行时域分析.由于混沌系统本身对高斯噪声的自免疫特性，因此本方法具有一定的抗噪性.仿真结果显示，该方法能有效的从时域上检测到微弱信号的起始点，其相对误差可达到10-3s.这对于心动信号中第一心音和第二心音的特征提取具有重要意义.

[1] 赖志慧，冷永刚，孙建桥，等.基于Duffing振子的变尺度微弱特征信号检测方法研究 [J].物理学报，2012，61（5）：050503-1-9.

[2] 何颖.一种新的弱信号混沌检测判据[J].电脑知识与技术，2012，8（8）：1891-1893.

[3] 韩振榕.基于混沌振子的微弱信号测频研究 [J].苏州大学学报：工科版，2009，29（6）：55-57.

[4] 范剑，赵文礼，王万强.基于Duffing振子的微弱周期信号混沌检测性能研究[J].物理学报，2013，62（18）：180502-1-6.

[5] 周玲，田建生，刘铁军.Duffing混沌振子用于微弱信号检测的研究[J].系统工程与电子技术，2006，28（10）：1477-1479.

[6] WANG J X，HOU X L.A method of weak signal detection based on duffing oscillator[C]//International Conference on e-Education，e-Business，e-Management and e-Learning.Sanya：IEEE Press，2010.

[7] LIU D W，YAO L.Influence of gauss white noise on the weak signal detection based on chaotic oscillator[C]//Wireless Communications Networking and Mobile Computing（WiCOM）. Chengdu：IEEE Press，2010.

[8] 庞春颖，韩立喜，刘记奎.HHT和提升小波包相结合的心音信号识别研究[J].信号处理，2014，30（1）：112-118.

[9] 刘萌萌，王敏，熊慧，等.基于EMD方法的心电信号带内噪声滤除[J].天津工业大学学报，2014，33（4）：62-66.

[10]王永生，姜文志，赵建军.一种Duffing弱信号检测新方法及仿真研究[J].物理学报，2008，57（4）：2053-2059.

[11]何坤，李健，乔强，等.非平稳环境下基于小波变换的信号去噪[J].信号处理，2005，21（3）：244-248.

[12]GONG J.Application of constructed complex wavelet in power quality disturbances detection[C]//Computing，Control and Industrial Engineering（CCIE）.Wuhan：IEEE Press，2011.

[13]YANG Zhanying，YU Yunxia.A new decomposition of multidimensional tensorial meyer mavelets[J].Journal of Southwest University：Natural Science Edition，2012，34（2）：74-77.

[14]王丽宁，徐妮妮.一种基于标准正交基的小波分解与重构的计算方法[J].天津工业大学学报，2006，25（6）：51-53.

[15]张刚，王颖，王源.基于锁相环的Duffing振子弱信号时域检测方法研究[J].科学技术与工程，2014，14（6）：13-19.

Starting point detection of weak signal in Duffing system

MIAO Chang-yun1，WANG You-xi1，GAO Hua1，MIAO Chun-jiao2
（1.School of Electronics and Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China；2.School of Electronics and Information Engineering，Beijing Jiaotong University，Beijing 100044，China）

In order to detect the starting point where a weak signal appears in the system from the time domain，an indirect method which can detect the starting point of weak signal based on Duffing system is propsed.Firstly，the weak signal is added with Duffing signal together，after the mixed signal is measured，the Duffing signal is eliminated from the mixed signal.Sencondly，the dmey wavelet is used to analyze the process of track deviation from the time domain，the starting point can be detected accurately.Because of the immune characteristics of chaotic system itself to Gauss noise，the proposed method has a certain anti-noise.The simulation results show that the proposed method can detect the starting point of the weak signal from time domain effectively，the relative error can reach 10-3s.It can be used to extract the characteristic parameters of heart sounds.

Duffing system；weak signal；starting point detection；dmey wavelet analysis

TN 911.7

A

1671－024X（2015）02－0080－04

2014-10-11

天津市高等学校科技发展基金计划项目（20110626）

苗长云（1962—），男，教授，博士生导师，研究方向为现代通信网络与系统、光电检测技术.E-mail：miaochangyun@tjpu.edu.cn