基于偏度与峰度的数据质量评估
2015-03-04崔书华刘军虎宋卫红
崔书华,李 果,刘军虎,宋卫红,沈 思
(1 宇航动力学国家重点实验室,西安 710043;2 西安卫星测控中心,西安 710043)
基于偏度与峰度的数据质量评估
崔书华1,2,李 果2,刘军虎2,宋卫红2,沈 思2
(1 宇航动力学国家重点实验室,西安 710043;2 西安卫星测控中心,西安 710043)
针对外弹道测量数据质量情况,拓展数据质量评价标准,提出了用分布偏度与峰度的分析方法描述数据质量状态。通过对跟踪测量数据进行分析验证,证明运用该方法可有效、直观的定量、定性的确定数据质量情况,为跟踪测量数据的使用提供了可靠性评价及使用决策。
偏度;峰度;数据分析;结果评估
0 引言
正态分布是外弹道测量数据质量分析最常使用的理论基础,通常也是统计测量数据随机误差的前提。所以,正态分布的检验在外弹道数据处理中是关键环节。检验一个样本是否服从正态分布的方法有很多,包括Kolmogorov检验、χ2拟合优度检验、Shapiro-Will检验和偏度-峰度检验等。但各有一些局限性,如Kolmogorov检验只有当假设的分布完全已知的时候才适用,χ2检验犯第二类错误(接受不正确零假设的错误)的概率往往较大,Shapiro-Will检验要求样本容量不大于50[1]等。而偏度-峰度法是一种快速、有效的正态检验方法,并且对样本的容量没有严格要求。现有文献中,在其他领域有较多的利用偏度-峰度法对数据进行分析、判断、决策,如文献[2-6]阐述了在各自的领域充分利用偏度-峰度技术取得的成果,但在外弹道测量数据质量分布的偏度和峰度分析方面极少。因此,文中选用偏度-峰度检验法对外弹道测量数据进行分析,通过偏度和峰度统计量检验样本是否服从先前的假设条件,以期更为客观地反映实测数据情况,并给出飞行目标弹道计算结果的可靠性评价及使用建议,为弹道的最优化连接和数据融合中的权值最优匹配做出决策。
1 方法介绍
在外弹道数据处理中,最典型的拟合方法就是利用最小二乘原理求解,即要求各数据偏离曲线函数值的误差的平方和最小。它通过最小化误差平方和找到一组数据的最佳函数匹配。通过拟合之后,获取随机变量,随机变量的三阶中心矩成为偏度,随机变量的四阶中心矩成为峰度。偏度和峰度是描述分布形状的重要数字特征。
1.1 偏度检验
偏度(skewness)是统计随机变量数据分布偏斜方向和程度的度量,是统计随机变量数据分布非对称的数字特征。偏度是利用三阶矩定义的,其物理含义为:
设x1,x2,…,xn是来自总体x的一个样本,则总体x的偏度可估计为:
(1)

若s>0,则称x的分布是正偏(或右偏),意味着在概率密度函数右侧的尾部比左侧长,绝大部分值位于平均值的左侧;若s<0,则称x的分布是负偏(或左偏),意味着在概率密度函数左侧的尾部比右侧长,绝大多数的值位于平均值的右侧;若s=0,则表示数值相对均匀的分布在平均值的两侧。|s|越大,说明分布偏斜得越厉害。对偏度值影响较大的是分布在其中一个方向上的尾部有拉长趋势的程度[4]。
1.2 峰度检验
峰度(kurtosis)是另一个反映随机变量分布形状的量,其是利用四阶矩定义的,物理含义为:
设x1,x2,…,xn是一组样本数据或一组有限总体数据,则其峰度的计算公式为:
(2)
峰度度量的是好数据的集中程度,峰度的取值范围是[-3,∞],正态峰度分布时为k=0,表示好坏数据差距处于一个合适的“度”;若k<0,则说明x分布尾部比正态分布的尾部细,表示好数据比较分散,好坏数据差距大,且|k|越大,尾部越细;若k>0,则说明随机变量x分布的尾部比正态分布的尾部粗,表示好数据比较集中,好坏数据差距小,并且k值越大,尾部越粗;若k为无穷大时,好坏数据没有差距,曲线变成一条直线。峰度可以用来比较已标准化了的各随机变量分布的尾部厚度。
1.3 检验方法
单纯利用偏度或单纯利用峰度来分析数据的分布情况是有缺陷的,只有两者同时进行检验才能保证对数据进行客观评价。即当s=0且k=0时,数据才能满足正态分布。但值得关注的是,数据的偏度和峰度在什么数值范围内才能认为数据分布可作正态近似,这很难给出一般性的答案[5]。所以,在外弹道测量数据进行综合分析时需要对随机误差数据同时进行偏度和峰度的检验,在确定数据融合的使用跟踪弧段时,需要综合考虑其他跟踪测量设备的数据情况,通过比对分析同跟踪弧段不同设备随机误差数据的偏度和峰度检验结果,确定最优权值的匹配,以期达到逼近实际目标飞行的弹道参数。
2 实例分析
以雷达跟踪测量数据为例(这里假设雷达测量数据已对系统误差进行了充分、可靠的修正),综合讨论其从测元数据到最终结果的质量情况,以及弹道高可信度选择及可使用弧段的确定。
2.1 拟合残差分析
图1~图3为某雷达跟踪测量数据的测距R、俯仰角E和方位角A数据应用最小二乘方法拟合后与原始测量数据的残差数据图。

图1 测距R拟合差残数据图

图2 俯仰角E拟合残差数据图

图3 方位角A拟合残差数据图
从图1~图3可以直观地看出,某些弧段跟踪测量的数据拟合残差较好。但是,如果定量的确定哪些跟踪测量数据可以满足正态分布的前提假设,并确定是否具有高的可使用度,还必须进一步进行分析。在下面的讨论中,将针对3个测元的跟踪测量弧段280~310 s的数据进行相关分析。
2.2 偏度峰度分析
图4~图6为雷达跟踪测量数据测距R、俯仰角E和方位角A数据随机差相对应的偏度与峰度统计数据图。

图4 测距R偏度及峰度数据图

图5 俯仰角E偏度及峰度数据图
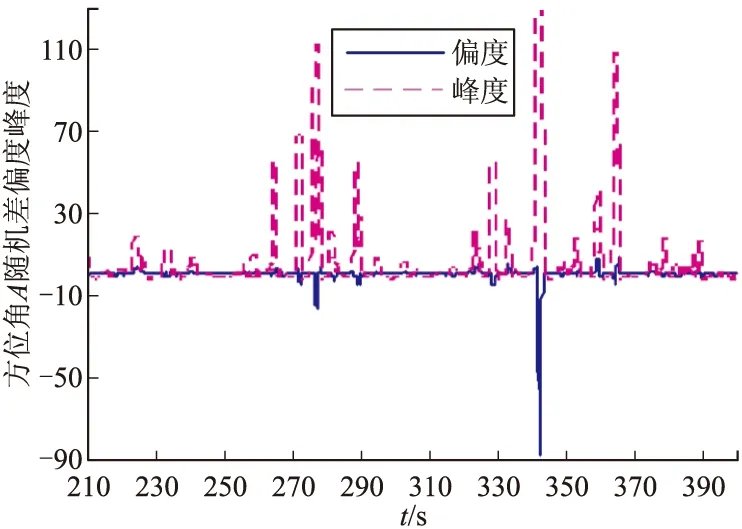
图6 方位角A偏度及峰度数据图
从图4~图6中可以看出,测距R的随机差数据的偏度和峰度在280~310 s弧段量值适度,其相对应弧段的方位角A随机误差的偏度和峰度也较其他弧段适度。为了便于飞行器目标定位精度情况的分析,选取具有相对较好偏度与峰度量值的280~310 s俯仰角E数据。
2.3 目标位置精度分析
上述分析的雷达跟踪测量的数据质量情况,为确定高可信度的使用弧段奠定了基础。为了行文方便,这里简单介绍单台雷达跟踪测量数据定位精度计算方法,式(3)为飞行器目标位置精度计算公式。
(3)
式中:R、E、A分别为测距、俯仰角和方位角的跟踪测量数据;σR、σE、σA分别为测距、俯仰角和方位角随机误差统计精度数据。
图7~图9为雷达跟踪测量数据单台定位后,飞行器目标在3个方向的位置精度数据图。

图7 目标在X方向的位置精度数据图
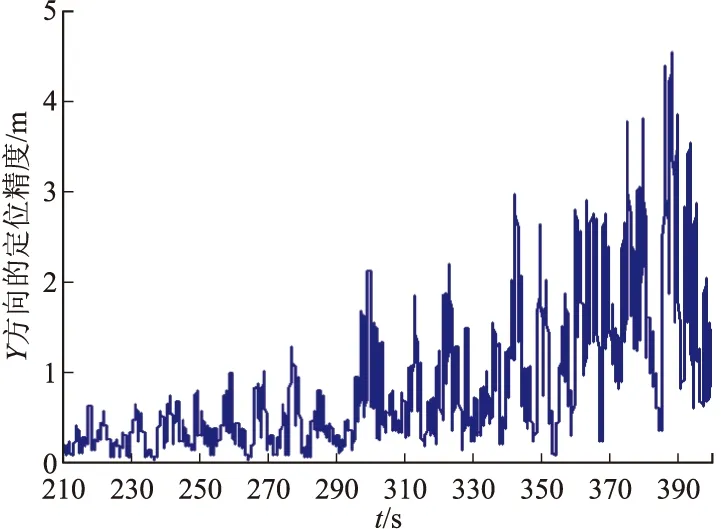
图8 目标在Y方向的位置精度数据图
图9 目标在Z方向的位置精度数据图从图7~图9精度数据来看,结合偏度-峰度的统计结果,可信度高的使用段应为280~310 s。相对来讲,虽然飞行目标在
Y
方向的210~250 s之间的定位精度较高,但结合式(3)和测距
R
的偏度与峰度综合考虑,此段的样本偏度有明显的左偏和右偏情况,同时也处在多峰的数据弧段,故此段数据可信度不如280~310 s的数据。
3 结论
通过上述分析可知,当跟踪测量数据的随机误差样本严重左偏、严重右偏、多峰或其他非正态分布,即检验样本不服从先前的假设条件时,会使目标的定位误差很大。只有综合考虑跟踪测量数据的偏度和峰度,才能准确判定数据的可使用跟踪弧段。所以,利用偏度-峰度的分析手段,不仅可以判断数据处理的可信区域,也能为获得更准确的定位精度寻求一种合理、科学、有效的手段。文中为外弹道测量数据评价与分析的方法,以及为后续弹道的数据融合和弹道连接提供了参考。
[1] 宋震龙, 将刚毅, 黄晃, 等. 基于偏度-峰度检验的无线局域网室内定位算法 [J]. 通信学报, 2012, 33(5): 99-105.
[2] 傅俊辉, 张卫国, 陆倩, 等. 考虑偏度风险和峰度风险的非线性期货套期保值模型 [J]. 系统工程, 2009, 27(10): 44-48.
[3] 王春峰, 庄泓刚, 房振明, 等. 多维条件方差偏度峰度建模 [J]. 系统工程理论与实践, 2010, 30(2): 324-331.
[4] 王学民. 偏度和峰度概念的认识误区 [J]. 统计与决策, 2008, 264(12): 145-146.
[5] 王学民. 关于样本均值的抽样分布能否作正态近似的探讨 [J]. 统计研究, 2005(7): 75-77.
Assessment and Analysis of Trajectory Measurement Data Based onSkewness and Kurtosis
CUI Shuhua1,2,LI Guo2,LIU Junhu2,SONG Weihong2,SHEN Si2
(1 State Key Laboratory of Astronautic Dynamics, Xi’an 710043, China; 2 Xi’an Satellite Monitor and Control Center, Xi’an 710043, China)
Due to quality of trajectory measurement data and extension of quality standard, distributed skewness and kurtosis analysis were put forward. It is proved that application of the method is able to determine quantitative and qualitative quality of data effectively and directly by analysis and verification of measurement data. Also, the method provides reliability evaluation and suggestion on measurement data.
skewness; kurtosis; data analysis; assessment of results
2014-12-17
国家自然科学基金(61473222;61231018;41274018)资助
崔书华(1964-),女,天津人,高级工程师,研究方向:外弹道数据处理方法及评估。
V557
A
