基于蒙特卡洛法的末敏弹命中点散布研究
2015-03-04许建胜戎永杰严智文
许建胜,苏 坡,戎永杰,严智文
(中国兵器工业第203研究所,西安 710065)
基于蒙特卡洛法的末敏弹命中点散布研究
许建胜,苏 坡,戎永杰,严智文
(中国兵器工业第203研究所,西安 710065)
弹药命中装甲目标的位置对其毁伤性能的评估具有重要参考价值。为了更好的评估末敏弹的毁伤性能,文中采用蒙特卡洛法对末敏弹的命中位置进行仿真,并结合各个参数对命中点的影响进行了分析。仿真结果表明水平方向的风和伞的摆动对末敏弹的识别率影响较大,滚转角和EFP战斗部散布是造成脱靶的主要原因。文中研究结果对末敏弹性能评估和改进提供了有价值的参考。
末敏弹;毁伤性能;命中点;蒙特卡洛法
0 引言
末敏弹是末端敏感弹药的简称,它是一种敏感式子母弹药,母弹为子弹载体并可装载多枚敏感子弹,子弹挂载多模敏感器具有末端敏感功能。在攻击目标时,母弹飞行至预定目标区域上空开舱抛出子弹。子弹被抛出后各自独立作用,按照预定流程进行稳态扫描,对目标进行自动探测、识别、定位、形成爆炸成形弹丸(EFP)从顶部攻击目标。可以说,末敏弹是一种真正意义上打了不用管的智能弹药[1-2]。
由于末敏弹作用原理的特殊性,且在稳态扫描时容易受许多因素的影响,因此末敏弹的毁伤效能不可能通过有限的实弹试验估计,数学仿真方法成为分析和计算末敏弹毁伤效能的有效手段。例如文献[3]采用神经网络对末敏弹的命中概率进行预测;文献[4]提出了基于支持向量机的末敏弹命中概率预测
模型;文献[5]采用蒙特卡洛法对末敏弹的毁伤特性进行仿真。这些方法基本上只是对末敏弹总体的命中概率进行了仿真,并未对末敏弹对装甲目标的命中点进行仿真。对于装甲目标来说,末敏弹命中不同的位置对其造成的毁伤效果不同,即末敏弹的命中点散布直接影响其毁伤性能,如击中坦克的发动机部分有很大概率会造成运动毁伤,击中坦克的炮塔部分很可能造成坦克的火力毁伤和乘载人员伤亡,因此通过末敏弹击中装甲目标位置对其毁伤效能进行评估,能够更加真实地反映实际情况,从而对末敏弹的进一步研究、设计和改进提供参考。
文中采用蒙特卡洛法对稳态扫描阶段末敏弹命中装甲目标的位置进行了仿真,并对敏感器稳态扫描不同参数的扰动对命中点的影响进行了仿真分析,为末敏弹毁伤效能的提高提供依据。
1 模型与方法
1.1 末敏子弹稳态扫描和命中模型
理想情况下,末敏子弹进入稳态扫描状态后,可认为末敏子弹扫描线在地面的轨迹为螺线(见图1)。扫描螺线上任一点的坐标可表示为:
(1)
式中:H表示子弹的稳态扫描起始高度;v表示落速;f表示转速;θ为扫描角;α0为扫描初始相位。扫描螺线的螺距Δ为:
(2)
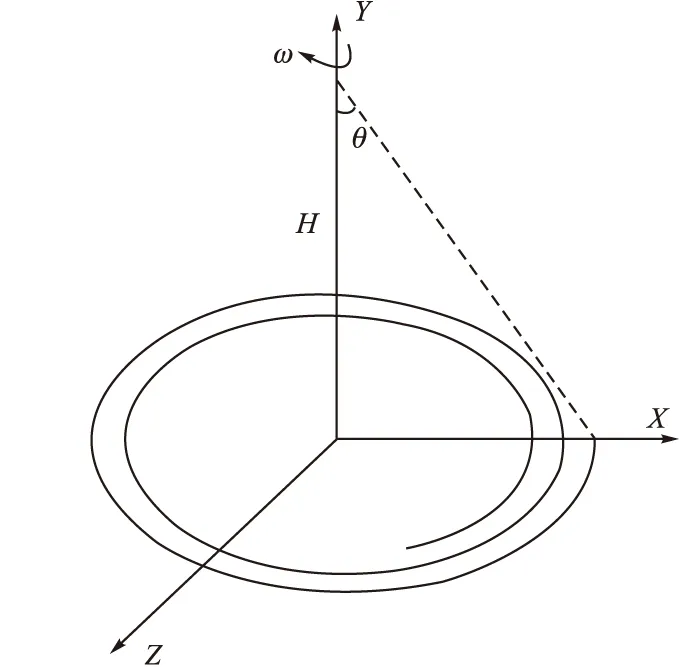
图1 末敏子弹稳态扫描示意图
末敏子弹通过敏感器目标响应信号(毫米波、红外)的幅值、距离差(激光)和目标信号的宽度,判断是否满足目标识别条件,并采用目标信号中心定位目标。当末敏子弹扫描到目标,且扫描线在目标上的长度大于等于2 m,认为目标被识别,且以目标上扫描线的中心为瞄准点,图2为示意图。图2(a)中,矩形框为装甲目标,目标尺寸为3.5 m×7 m,点集为扫描螺线轨迹;图2(b)为图2(a)中矩形装甲目标的局部放大图,其中实心点表示扫描线经过目标的轨迹,空心圆点表示经过目标扫描线的中心点,即命中点。

图2 理想情况下目标识别与打击示意图
以上为理想情况下末敏子弹对目标的扫描、识别和打击。在实际中,由于:1)扫描平台参数存在扰动,这些参数可看作是符合某种分布的随机变量;2)EFP战斗部存在散布误差;3)外界环境条件的干扰,如风;4)敏感轴相对于威力轴的前置角存在散布;5)滚转角等这些因素的存在,致使末敏子弹实际打击点较理想打击点产生散布,和预期效果不一致,甚至产生脱靶。下面分析上述因素对打击位置的影响。
1)扫描平台参数变化
扫描平台参数主要包括落速、转速和扫描角。落速的变化会导致扫描螺线螺距发生变化,影响弹目交汇的概率,而对目标识别后的打击点不产生影响。转速和扫描角的变化同样会导致扫描螺线螺距发生变化,影响弹目交汇概率,同时会对目标识别后命中点的位置产生影响。
一般末敏子弹敏感轴前置于威力轴,以保证末敏子弹探测并识别目标后延迟一定时间,威力轴才扫过目标中心并起爆战斗部,延迟的时间是根据理想的平台参数(主要是转速和扫描角)计算得到的,因此转速和扫描角的变化会导致打击时刻提前或滞后。假设扫描到目标的宽度为l,敏感器前置角大小为δ,末敏子弹此时的高度为h,延迟时间的计算公式如下:
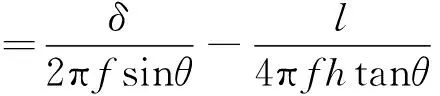
(3)
根据式(3)可得Δt延为:
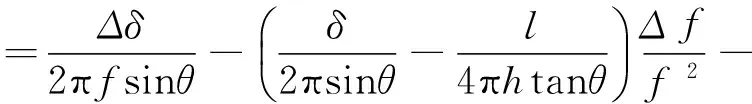
(4)
2)EFP战斗部的散布
由于EFP有一定的散布,会导致实际命中点落在瞄准点的周围,并呈圆形散布。
3)风的影响
一般来讲,风不会直接影响打击点的位置,但是风会使旋转伞产生摆动,影响到扫描角,从而间接对命中点位置产生影响。另外,风向可以分为水平方向和竖直方向。水平方向的风会使末敏子弹产生漂移,竖直方向的风会影响落速,二者皆会影响弹目交汇概率。
4)前置角的散布
起爆延迟时间是根据固定的前置角和稳态扫描平台参数计算得到,实际中前置角存在散布,因而会影响到打击点的位置。
5)滚转角的散布
理想情况下,末敏子弹的威力轴与敏感轴在同一个圆周上,即滚转角为零。实际上,由于子弹摆动二者通常不在同一个圆周上,存在滚转角,滚转角的存在会使打击点在扫描的径向方向出现散布。
1.2 蒙特卡洛方法
蒙特卡洛方法也称随机模拟方法,是一种数学统计试验方法,它利用各种不同随机变量的抽样序列模拟实际的概率统计模型,求得问题数值解的统计估计值。蒙特卡洛方法的一般流程如下:1)构造数学模型;2)建立随机变量抽样方法;3)产生数学模型中随机变量的值;4)根据随机变量的值解算模型,并对多次解算结果进行统计处理,求得关心的统计量。
2 仿真实验与结果分析
下面,采用蒙特卡洛法对其命中点位置进行仿真实验。
2.1 仿真条件
仿真中,固定子弹位置为坐标原点,子弹从初始120 m开始进入识别,低于20 m停止识别;装甲目标尺寸为3.5 m×7 m,目标中心等概率落在坐标原点周围120 m×120 m的区域,即目标中心坐标xt~U[-60 m,60 m],zt~U[-60 m,60 m],这样能确保子弹能进入作用流程;参照德国SMArt末敏子弹指标设:子弹转速f~N[3 r/s,0.167 (r/s)2],理想转速fi=3 r/s;子弹初始相位α0~U[0,2π];理想扫描角θi=π/6;伞摆动振幅A=10°,摆动频率fb~U[3 Hz,4 Hz],初始相位φ0~U[0,2π];前置角δ~N[π/90,0.0019],理想前置角δi=π/90;落速v对打击点位置不影响,v=13 m/s;战斗部相对于扫描线偏差EX~N[0 m,0.44 m2],EZ~N[0 m,0.44 m2];水平方向风的风速vw~U[0 m/s,10 m/s],风向αw~U[0,2π];其他环境条件为标准气象条件。这里,U[a,b]表示[a,b]范围内的均匀分布;N[μ,σ2]表示服从均值为μ、方差为σ2的正态分布。
2.2 结果与分析

图3 仿真结果
采用蒙特卡洛方法各进行10 000次仿真。图3给出仿真结果,其中图3(a)为所有条件均在理想情况下命中点的仿真结果;图3(b)为所有因素综合作用命中点的仿真结果;图3(c)为仅转速、目标中心位置、扫描初始相位为随机变量,而其他因素均为理想情况命中点的仿真结果;图3(d)为仅前置角、目标中心位置、扫描初始相位为随机变量,而其他因素均为理想情况打击点的仿真结果;图3(e)为存在伞的摆动、目标中心和初始扫描相位为随机变量,而其他因素均为理想情况下命中点的仿真结果;图3(f)为仅滚转角存在散布,而其他因素均为理想情况下命中点的仿真结果;图3(g)为战斗部存在散布、目标中心位置和扫描初始相位为随机变量,其他因素均为理想情况命中点的仿真结果;图3(h)为仅存在水平方向的风,其他因素均为理想情况命中点的仿真结果。
更进一步,如图4所示可以将典型的坦克装甲目标的平面跟据构造简单的划分为5个部分:1-左履带、2-右履带、3-前装甲、4-炮塔部分、5-动力部分。分别统计落入各个部分的百分比,统计结果如表1。表1结果表明,伞的摆动和水平方向的风对末敏弹的识别率影响较大,而滚转角和EFP战斗部的散布是造成末敏弹脱靶的主要因素。

图4 坦克的平面图

表1 打击位置统计
3 结论
文中采用蒙特卡洛法对末敏子弹命中装甲目标位置进行仿真研究,并对相关因素的影响进行了仿真和分析。仿真结果表明末敏子弹的识别率受伞摆动和水平方向风的影响较大,滚转角和EFP战斗部散布是造成末敏子弹脱靶的主要原因。研究结果对末敏弹毁伤效能的分析、评估和改进提供了有价值的参考。
[1] 杨绍卿. 灵巧弹药工程 [M]. 北京: 国防工业出版社, 2010.
[2] 杨绍卿. 末敏弹系统理论 [M]. 西安: 陕西科学技术出版社, 2009.
[3] 唐克, 王存威, 卢金星. 基于神经网络和Matlab的末敏弹系统效能灵敏度仿真 [J]. 兵工自动化, 2010, 29(7): 90-93.
[4] 唐克, 王存威. 末敏弹命中概率预测模型研究 [J]. 舰船电子工程, 2011, 31(3): 119-121.
[5] 王晓波, 姚俊, 马金明. 蒙特卡洛法在末敏弹毁伤概率计算中的应用 [J]. 沈阳理工大学学报, 2011, 30(5): 50-53.
Research on the Hitting Point Distribution of Terminal Sensing Ammunition Based on Monte-Carlo Method
XU Jiansheng,SU Po,RONG Yongjie,YAN Zhiwen
(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)
The hitting point plays an important role on evaluating damage performance of ammunition. To better evaluate damage performance of terminal sensing ammunition, in this paper, a Monte-Carlo method is utilized to simulate the hitting point of terminal sensing ammunition. Meanwhile, the related parameters are also analyzed. The simulation results indicates that the disturb of parachute and the horizontal wind has great influence on the recognition rate of terminal sensing ammunition, the rolling angle and the distribution of EFP warhead are the main reasons for missing the target. The research results in this paper can provide valuable reference for the damage performance evaluation and improvement of terminal sensing ammunition.
terminal sensing ammunition; damage effectiveness; hitting point; Monte-Carlo method
2015-07-21
许建胜(1961-)男,陕西西安人,研究员,研究方向:信号处理与目标识别。
TJ414.3
A
