Application of adaptive Kalman filter in rocket impact point estimation
2015-03-03YANXiaolongCHENGuoguangBAIDunzhuo
YAN Xiao-long, CHEN Guo-guang, BAI Dun-zhuo
(1. College of Mechatronic Engineering, North University of China, Taiyuan 030051, China;2. Yuxi Industries Group Co.,Ltd., Nanyang 473000, China)
闫小龙1, 陈国光1, 白敦卓2
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 豫西工业集团有限公司, 河南 南阳 473000)
Application of adaptive Kalman filter in rocket impact point estimation
YAN Xiao-long1, CHEN Guo-guang1, BAI Dun-zhuo2
(1.CollegeofMechatronicEngineering,NorthUniversityofChina,Taiyuan030051,China;2.YuxiIndustriesGroupCo.,Ltd.,Nanyang473000,China)
In order to measure the parameters of flight rocket by using radar, rocket impact point was estimated accurately for rocket trajectory correction. The Kalman filter with adaptive filter gain matrix was adopted. According to the particle trajectory model, the adaptive Kalman filter trajectory model was constructed for removing and filtering the outliers of the parameters during a section of flight detected by three-dimensional data radar and the rocket impact point was extrapolated. The results of numerical simulation show that the outliers and noise in trajectory measurement signal can be removed effectively by using the adaptive Kalman filter and the filter variance can converge in a short period of time. Based on the relation of filtering time and impact point estimation error, choosing the filtering time of 8-10 s can get the minimum estimation error of impact point.
rocket; adaptive Kalman filter; outliers; impact point estimation
0 Introduction
With the increasing requirements for rocket firing accuracy, rockets must be corrected in the process of flight by estimating the rocket flight status and predicting the impact point based on the observation data of flight rocket from radar, global positioning system (GPS), etc., then comparing the impact point with the target and calculating the error, finally correcting rockets trajectory according to the error.
In this paper, we get rocket flight trajectory by means of three-dimensional data radar. Because of big radar errors in fight process, which impacts the data for impact point estimation of the rocket, radar signal noise must be filtered out for getting correct trajectory data, including random noise in actual probing radar, the noises called “outliers” from the actual noise with big errors, which have a big impact on filtering algorithm and affect the accuracy of the results. Therefore, Kalman filter algorithm with outliers removing is proposed in this paper, which improves the accuracy of rocket impact point estimation effectively[1].
1 Rocket exterior trajectory filtering and extrapolation model
After getting the radar measurement data, according to the ballistic trajectory model, the measured and extrapolated placement is filtered, then data error is fed back in time, finally the rocket trajectory is corrected using rocket actuator. Because rocket trajectory corredtion needs to calculate and estimate the impact point in time and accurately, we select the particle trajectory model with high-speed calculation to meet the requirement of high-speed and high-accuracy calculation. The model is written
(1)

Wesetx1, x2, x3, x4, x5, x6, x7, x8, x9andx10asstatevariablesofKalmanfilter,thusthereis
whereCbis the projectile motion, and it can be set at zero[2];εx,εyandεzare the positioning errors.
Then we can get the system state equation as
(2)
where W(k)iszero-meanrandomnoiseinterference.
2 Filtering measurement equation
Based on the measurement results with Slant ranger, azimuth angleβand elevation angleεby means of three-dimensional data radar, we can obtain the relation between the radar measurement value and the ground coordinate system as
(3)
where (xo,yo,zo) are the coordinate of the radar antenna center in the ground coordinate system[3].
The coordinate radar measurement array isz=(r,β,ε). Vkisradarmeasurementnoise.AssumethatVkiszero-meanGaussianwhitenoise,andthediscreteformofthemeasurementnoisecovariancematrixisgivenby
(4)

Inthecourseofrocketlaunching,radarcoordinatesystemisnotjusttheemplacementcoordinate.Therefore,weneedtoconvertthetwocoordinatesystems[4],andtheconversionrelationis
(5)
whereεX,εYandεZarethreerotationanglesofthethree-dimensionalspacerectangularcoordinatewhentransformation; R1(εX), R2(εY)andR3(εZ)arecorrespondingrotationmatrices;andR0is expressed as
Measurement equation can be obtained as
(6)
3 Kalman filter
Kalman filter equations are divided into two parts: one is Kalman filter equation, which is responsible for the estimated path forward of the state; the other is Kalman filter gain matrix recurrence equation, which is responsible for feedback priori estimation and correction for the prediction[5]. The discrete Kalman optimal estimation equations are as follows:
1) Optimal prediction estimation equation
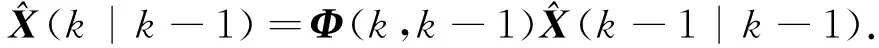
(7)
2) Optimal filtering estimation equation
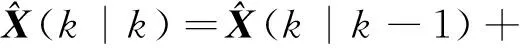

(8)
3) Optimal filter gain matrix equation
(9)
4) Optimal prediction estimation error variance matrix

(10)
5) Optimal filtering estimation error variance matrix equation
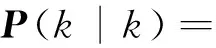
(11)
The statistical propertiesE{X(0)} andP(0) of state vector X(0)areknownatt0.Inordertoobtainunbiasedestimates,weset

4 Identification and treatment of outliers
Actually measured signals must go through transmission system, data acquisition system, conversion system and other systems, and then the target digital signals are sent to Kalman filter, which will not only have random noise, but also may generate some outliers with large difference compared with actual data by outside irregular interference. The existence of these outliers has great influence on the results of Kalman filter[6].
We set

(12)
(13)
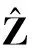
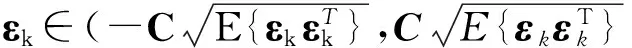
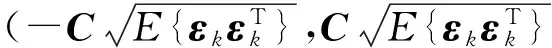
In the above equations,Cis 3×1 dimensional vector which represents an allowable range of measured value error based on actual trajectory metrology tool, and it can be changed according to the precision settings with different measurement tools at different times[7]. By means of this identification method, we can determine which measured value of each component exceeds the limit error. Whenεkis not in allowable error range, we need to modify the predicted value, thus the optimal filtering estimation equation can be expressed as
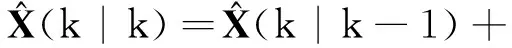
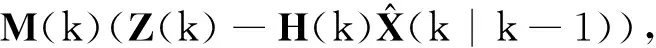
(14)
whereM(k)=iK(k),i∈[0,1].
That is, changing the filter gain matrix equation can make filter gain change due to the presence of outliers. This makes optimal filter estimation equation correct, eliminates the negative filtering effect that brings outliers to measurement information. Absolutely, when the measured value does not exceed the allowable range and setsi=1, the filter gain matrix equation will not be changed.
5 Numerical simulation
Inordertotesttheactualfilteringeffectofthefilter,itisneededtodonumericalsimulationcalculation.Inthispaper,weselecttherocketwithfiringrangeof40kmastheexampleofthesimulation,using5Dtrajectorymodeltocalculatethetrajectoryrawdata,addingGaussianwhitenoisewithmeanofzerointotheradarnoise,andtakinglargeerrorswithinuncertainperiodasradarmeasurementsoutliersforformingthree-dimensionaldataradartomeasuredata[8].UsingKalmanfilterwithoutliertreatmenttodiscriminate,process,andfilteroutliersintheradarmeasureddata,trajectoryisextrapolatedusingparticleexteriortrajectoryequationandimpactpoint(X, Z)isestimated.Afterthesimulatedprojectilelaunchesfor2.5s,theradarbeginstotrackthetargetandthesamplingintervalis0.1s.Whenthesimulatedradarworksforabout45s,thetrajectorydatastarttobefiltered.Whencontinuousmonitoringtimeis70s,thefilteringprocessisover.Figs.1, 2and3aretheresultsofoutliersremovingandfilteringindifferentdirections.
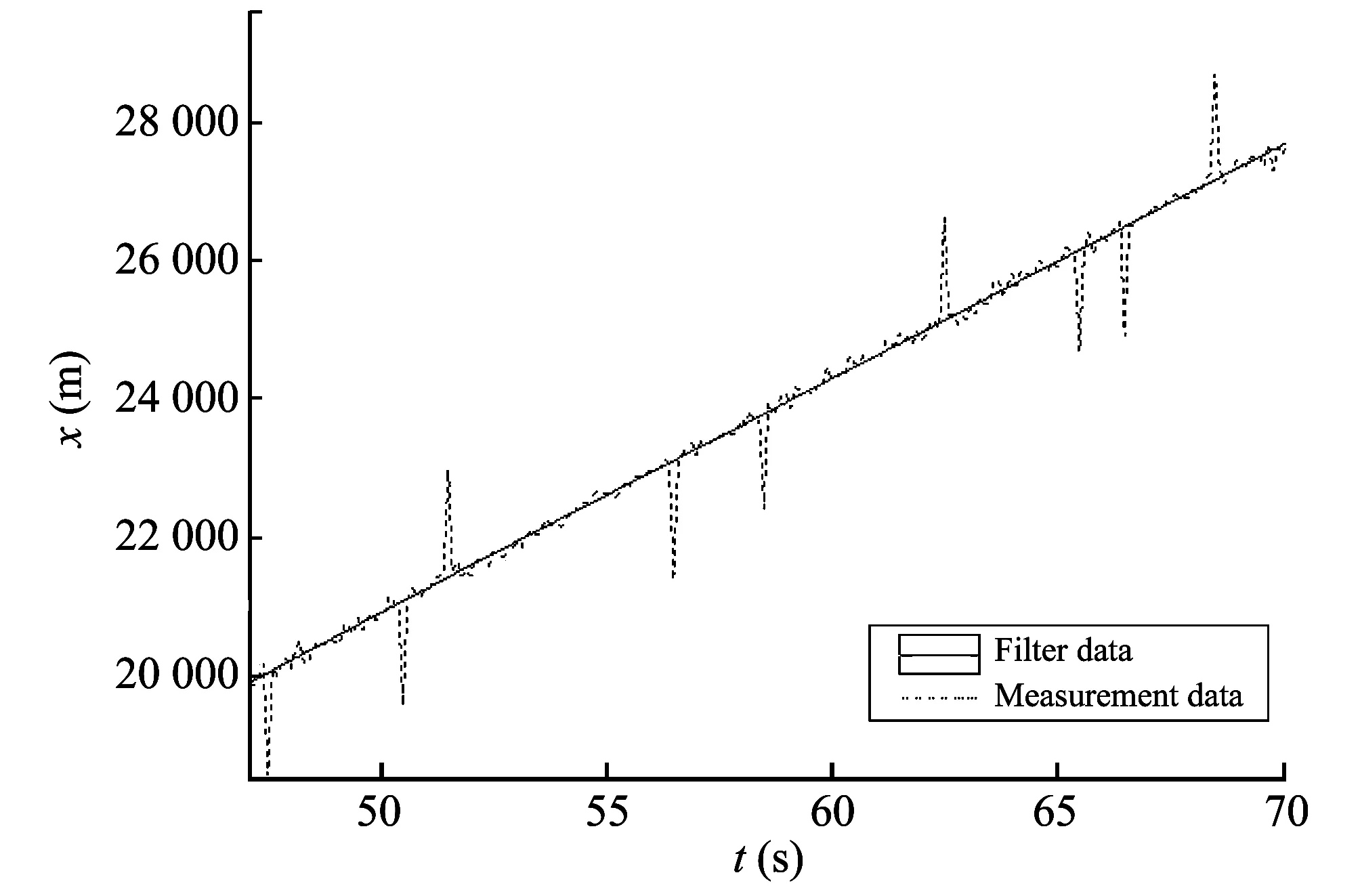
Fig.1 Data processing on X axis
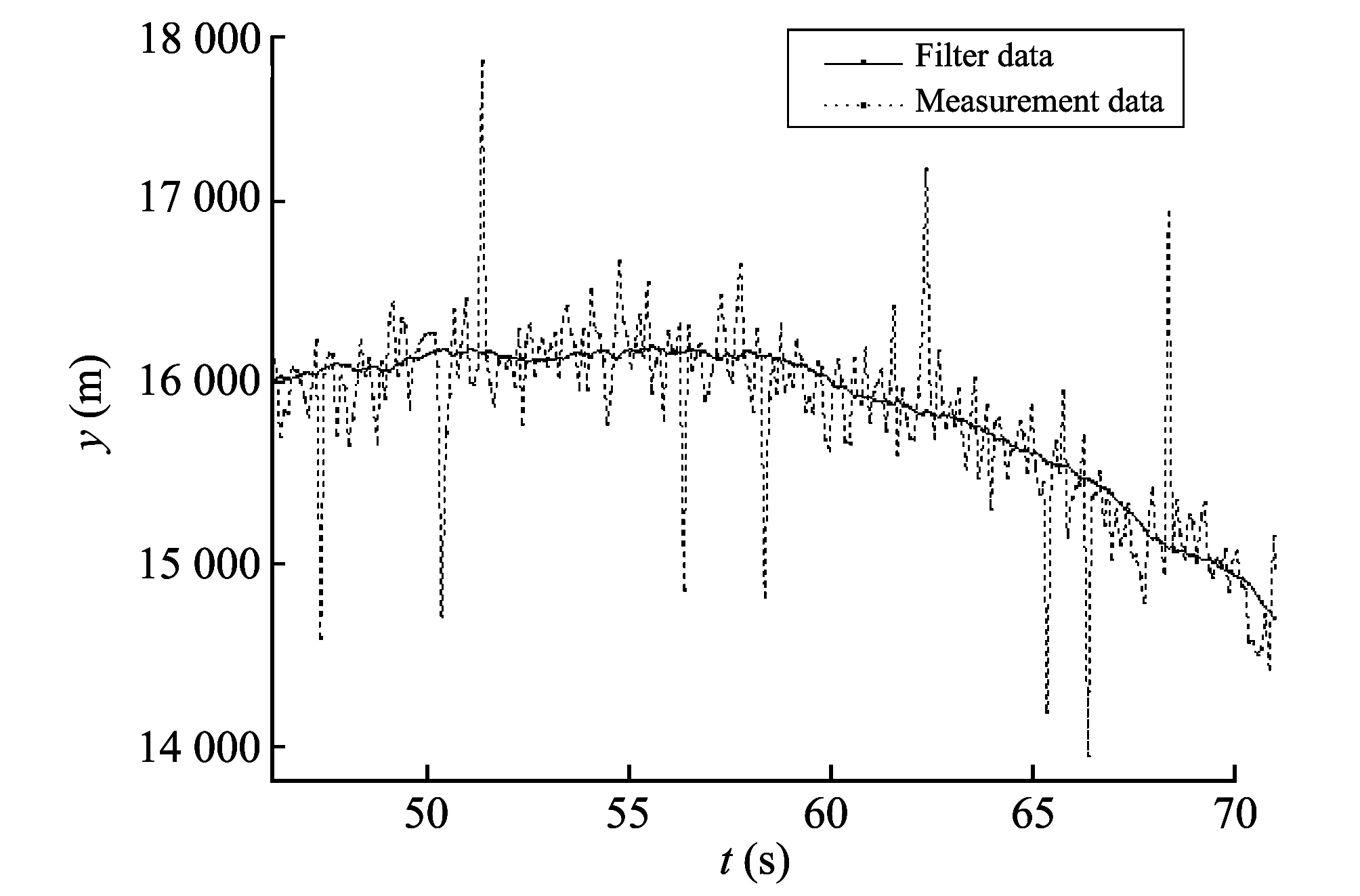
Fig.2 Data processing on Y axis

Fig.3 Data processing on Z axis
After getting the filtered and removed outliers, we select filtering results at the time 70 s and use the particle trajectory equation for rocket impact point (X,Z) estimation. By comparing the estimation to the actual trajectory, the impact point estimation error is got. Filter variances inX,YandZdirections are shown in Fig.4. It can be seen that the filter variance converge stabilizes quickly after 20 s.

Fig.4 Filter variances in X, Y and Z directions
Fig.5 shows the relation of filtering time and impact point estimation error which is extrapolated from the particle trajectory equation according to rocket flight data at the end of filtering. It can be seen that there is a close relation between the impact point estimation accuracy and filtering time. The impact point estimation accuracy increases with the increase of filtering time, but the accuracy increases slowly after a period of time[9]. It should be reasonable to select the time of radar tracking rocket and radar data filtering time, so that we can get high estimation accuracy of placement in a relatively short time.
The numerical simulation results show that for the 122 mm rocket, if the sampling time is 0.1 s, selecting radar tracking and filtering time for 8-10 s can get good results.

Fig.5 Relation of filtering time and impact point estimation error
6 Conclusion
In this paper, the rocket trajectory data measured by three-dimensional data radar with random noise signals were filtered based on Kalman filter with adaptive gain matrix according to presence of outliers, by using extrapolation particle trajectory equation to estimate impact point according to trajectory data after filter provides effective data for rocket correction. Numerical simulation was conducted using the generated trajectory data and the results show that when there are outliers and large random noise of radars, using the designed filter can get trajectory data which is close to the true value. In different times of radar tracking and filtering, the impact point estimation accuracy will be different. With the increas of radar tracking and filtering time, the impact point estimation accuracy increases continuously. But when the time increases to a certain level, the accuracy tends to be stable.
[1] WANG Zhi-xian. Optimal state estimation and identification system. Xi’an: Northwestern Polytechnical University Press, 2004.
[2] SHI Jing-guang, XU Ming-you, WANG Zhong-yuan, et al. Application of Kalman filtering in calculation of trajectory falling point of trajectory correction projectiles. Journal of Ballistics, 2008, 20(3): 41-44.
[3] GAO Ning, ZHOU Yue-qing, YANG ye, et al. Adaptive Kalman filter algorithm with fault-tolerant improvement. Journal of Chinese Inertial Technology, 2003, 11(3): 25-28.
[4] ZHANG Yuan, CHEN Yong, WU Hao. Study of ballistic missile impact point prediction. Missiles and Space Vehicles, 2014, (3): 5-10.
[5] LI Guang-jun, LI Zhong, CUI Ji-ren. Research on new Kalman filter restraining outliers. Computer Applications and Software, 2013, 30(1): 136-138.
[6] ZHAO Han-dong, LI Qiang, JIAO Jun-hu, et al. The study on improvment of firing accuracy of rocket projectile using impact point predication guidance law. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(3): 169-172.
[7] YANG Shu-xing, ZHANG Cheng, ZHU Bo-li. Unsophisticated control method for long-range rockets. Transactions of Beijing Institute o f Technology, 2004, 24(6): 486-491.
[8] XU Ming-you. Advanced exterior ballistics. Beijing: High Education Press, 2003.
[9] HAN Zi-peng. Exterior ballistics of projectiles and rockets. Beijing: Beijing Institute of Technology Press, 2008.
自适应卡尔曼滤波器在火箭弹落点估计中的应用
利用雷达对火箭弹一段飞行过程中的参数进行量测, 对火箭弹落点进行了准确估计, 实现了火箭弹的轨迹修正。采用具有自适应调节滤波增益矩阵的卡尔曼滤波器, 结合质点弹道模型, 建立了自适应卡尔曼滤波弹道模型, 完成了对三坐标雷达探测的一段火箭弹飞行参数的野值处理与滤波, 并对火箭弹落点进行外推。 数值仿真结果表明, 经自适应调节的卡尔曼滤波器滤波后, 弹道量测信号中的野值与噪声被有效去除, 且滤波方差可以在短时间内收敛。 根据滤波时间与落点估计误差的关系, 采用滤波时间为8-10 s方案, 可得到最佳的落点估计。
火箭弹; 自适应卡尔曼滤波器; 野值; 落点估计
YAN Xiao-long, CHEN Guo-guang, BAI Dun-zhuo. Application of adaptive Kalman filter in rocket impact point estimation. Journal of Measurement Science and Instrumentation, 2015, 6(3): 212-217.[
闫小龙1, 陈国光1, 白敦卓2
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 豫西工业集团有限公司, 河南 南阳 473000)
10.3969/j.issn.1674-8042.2015.03.002]
YAN Xiao-long (13994230892@139.com)
1674-8042(2015)03-0212-06 doi: 10.3969/j.issn.1674-8042.2015.03.002
Received date: 2015-05-11
CLD number: TJ415 Document code: A
猜你喜欢
杂志排行
Journal of Measurement Science and Instrumentation的其它文章
- Modal analysis of 4-cylinder engine crankshaft based on ANSYS Workbench
- Simulation of small-aperture deep hole drilling based on ABAQUS
- Investigation on nonlinear rolling dynamics of amphibious vehicle under wind and wave load
- Numerical simulation of two-phase flow field in underwater sealing device based on dynamic mesh
- Analysis of movement laws of fragment and shock wave from a blast fragmentation warhead
- X-ray image distortion correction based on SVR
