高等数学在化学热力学中的应用

路庆华, 张坤玲

(1.石家庄信息工程职业学院 高职教育研究所，河北 石家庄 050035；2.石家庄职业技术学院 化学工程系，河北 石家庄 050081)



高等数学在化学热力学中的应用

路庆华1, 张坤玲2

(1.石家庄信息工程职业学院 高职教育研究所，河北 石家庄 050035；2.石家庄职业技术学院 化学工程系，河北 石家庄 050081)

在分析状态函数和全微分性质、热力学状态函数间重要关系式的基础上，借助实例分析了高等数学在化学热力学中的应用.用高等数学的方法可以证明化学热力学的结论，推导相关公式；激发学生学习兴趣，培养学生运用数学知识分析、解决实际问题的能力.

高等数学；物理化学；化学热力学；应用

物理化学是一门理论性及实践指导性都很强的学科，其特点是理论抽象、逻辑性强、公式繁多且适用范围有严格的限制.在物理化学公式推导、定性分析及定量计算的过程中，数学严谨的逻辑思维和解题方法应用十分广泛.物理化学课程自始至终贯穿着数学理论和知识，数学方法为物理化学的深入研究提供了强有力的工具.因此，学习物理化学，高等数学是必不可少的工具.本文通过实例说明如何将高等数学知识应用于化学热力学中.

1 状态函数和全微分性质

系统的状态是其所有宏观性质的综合表现.状态性质可描述系统状态的各种性质，又称为状态函数.状态函数的特征可以用数学语言来描述.

(1)系统的状态确定之后，所有的状态函数都有定值.例如，对于一定量的纯物质单相系统，有V=f(T，p)的函数关系.

(2)系统状态函数的改变值只与始态和终态有关，而与变化的途径无关，即

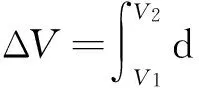
(3)循环过程状态函数的变化值为零，即ΔV=∮dV.

状态函数在数学上具有全微分的性质，即状态函数的微小变量是热力学函数的全微分.

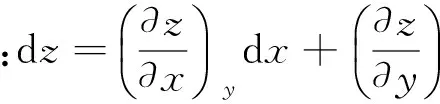
热力学在解决实际问题时就是以状态函数的这些性质为基础的.

2 热力学状态函数间的重要关系式

2.1 热力学基本方程

对于封闭系统的变化过程，根据热力学第一定律、热力学第二定律及对焓、吉布斯函数、亥姆霍兹函数的定义式微分，通过数学方法推导可得热力学基本方程如下：

dU=TdS-pdV，

dH=TdS+VdV，

dA=-SdT-pdV，

dG=-SdT+Vdp.

对简单的p,V,T变化过程，可用热力学基本方程的积分计算U，H，A，G的变化值.

2.2 对应系数关系式

热力学基本方程dU=TdS-pdV,可表示为U=f(S,V).

利用状态函数的全微分性质有:

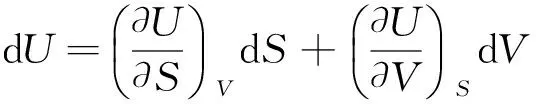
根据对应项相等原理，可得

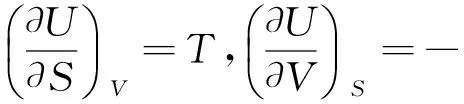
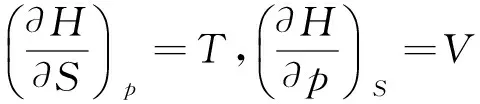
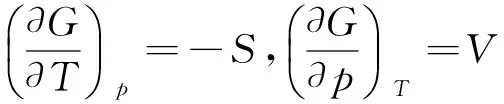
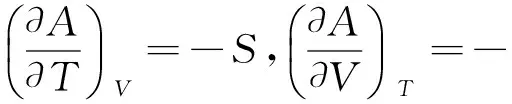
这8个关系式被称为对应系数关系式，它们给出了一个热力学函数随另一变量的变化率与某一状态函数在数值上的等量关系，在分析和证明问题时经常用到.

2.3 麦克斯韦关系式

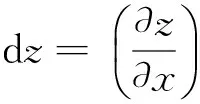
将此关系用于dU=TdS-pdV，可得

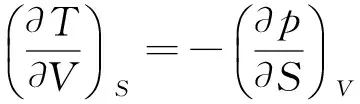
同理，另外3个热力学基本方程为：

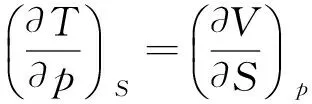
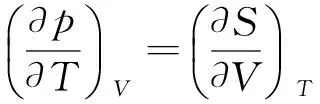
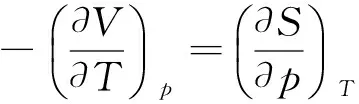
这4个关系式被称为麦克斯韦关系式.它们将系统不可直接测定的热力学状态函数与可直接测定的状态函数p，V，T联系起来，分别表示系统在同一状态的两种变化率数值相等，常用于某种场合等式两边的代换.

3 运用数学方法证明化学热力学的结论

例1 试证明理想气体的热力学能和焓只是温度的函数.

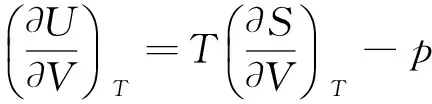
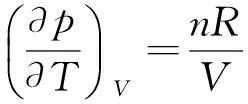
同理，由热力学基本方程dH=TdS+Vdp得，

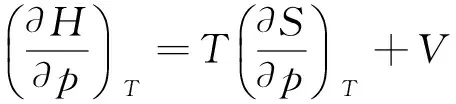
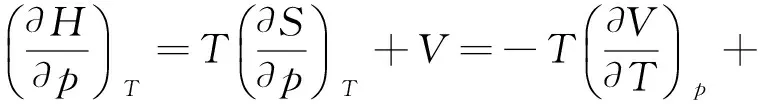
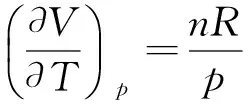
即H=f(T)，理想气体的焓只是温度的函数.

4 运用数学方法推导公式

化学热力学的特点是公式多，而这些公式的推导和应用都离不开高等数学知识，尤其是微积分部分.

4.1 体积功计算公式

热力学将在一定环境压强下系统体积发生变化时与环境交换的功称为体积功.微小体积功的计算公式为δW=-p环dV.

若外压恒定，即p环=常数，则W=-p环(V2-V1).

4.2 可逆体积功计算公式

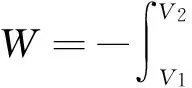
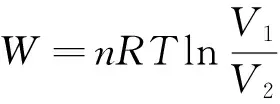
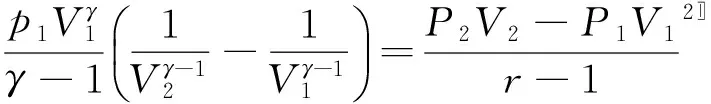
例2 1 mol理想气体A(g)，沿Vm=CT2(式中C为常数)可逆途径升温2 K，求此过程的W.

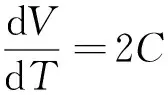
根据理想气体状态方程pVm=RT得,pCT2=RT,所以p=R/CT，因此，

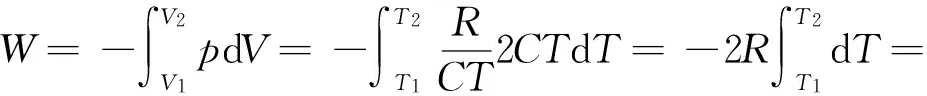
5 物理量的表示及相关计算

5.1 热容的定义

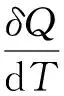
在化学热力学计算中常用到定压摩尔热容Cp,m和定容摩尔热容CV,m.

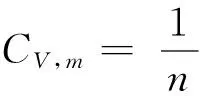
5.2Cp,m与CV,m的关系

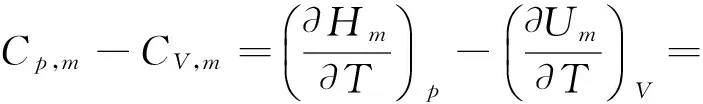
对于1 mol的纯物质，设Um=f(T,V)，

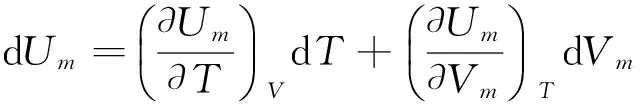
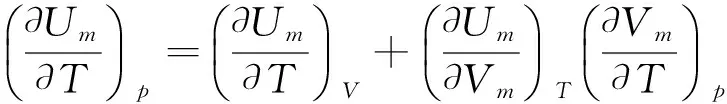
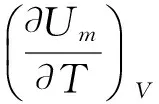
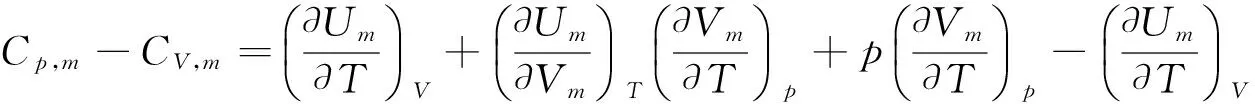
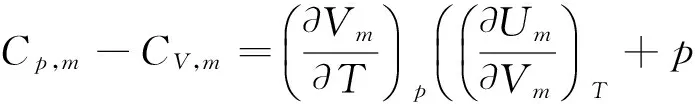
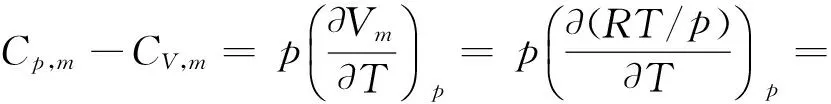
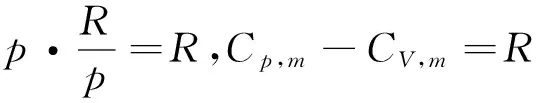
5.3 理想气体ΔU与ΔH的计算

一定量的理想气体的热力学能可以表示为温度和体积的函数U=f(T,V)，

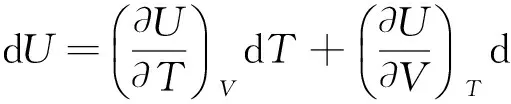
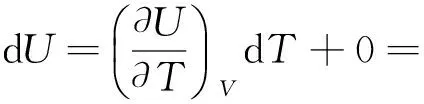
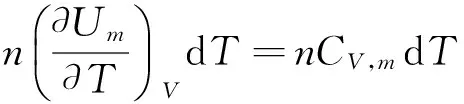
同理，一定量的理想气体的焓可以表示为温度和压强的函数H=f(T,p).

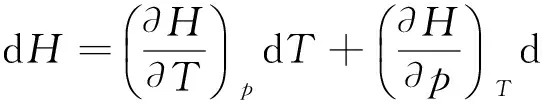
因为理想气体的焓只是温度的函数，即

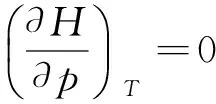
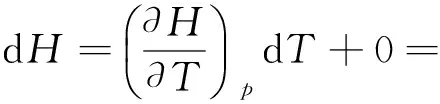
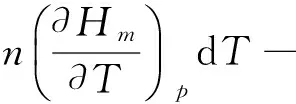
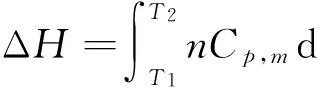
即理想气体ΔU与ΔH的计算不受过程恒容与恒压条件的限制.

例3 已知O2在273～3800 K的温度范围内,定压摩尔热容与温度的关系式服从Cp,m(J·K-1·mol-1)=28.17+6.297×10-3T/K-0.7494×10-6T2/K2,今将1 mol O2(g)在空气中自298 K加热到398 K，计算需要多少热量？系统的ΔH与ΔU为多少？

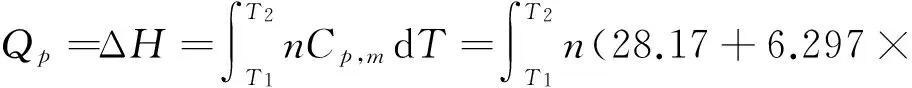
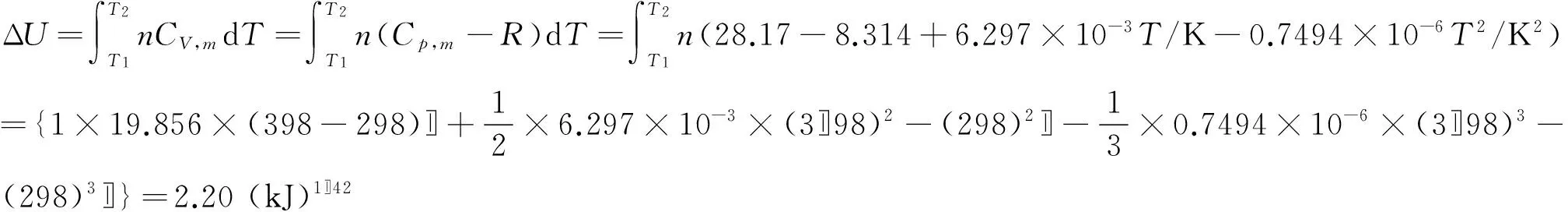
通过实例可以看出，高等数学知识在化学热力学中的应用十分广泛.教师在教学过程中，要善于运用高等数学的基本理论和技巧，培养学生逻辑推理问题、抽象概括问题、熟练运算问题、综合分析并解决实际问题的能力，而这对于激发学生学习兴趣，启发学生正确理解所学知识，提高教学质量具有十分重要的意义.

[1]张业．物理化学学习指导．北京：化学工业出版社， 2008.

[2]张坤玲．物理化学．大连：大连理工大学出版社，2014:22.

[3]肖衍繁，李文斌．物理化学．天津：天津大学出版社，2004:131.

责任编辑：金 欣

The application of advanced mathematics in chemical thermodynamics

LU Qing-hua1， ZHANG Kun-ling2

(1.Institute of Higher Vocational Education，Shijiazhuang Vocational College of Information Technology，Shijiazhuang，Hebei 050035，China;2.Department of Chemistry，Shijiazhuang Vocational Technology Institute，Shijiazhuang，Hebei 050081，China)

This article discusses the application of advanced mathematics in chemical thermodynamics and analyzes the properties and the thermodynamic function.The conclusion can be proved and deduced with relative formulae of advanced mathematics.

advanced mathematics; physical chemistry; chemical thermodynamics; application

2015-09-21

路庆华(1963-)，男，河北石家庄人，石家庄信息工程职业学院副教授.

1009-4873(2015)04-0062-04

O13；O642.1

A