形象认识微积分

王玉苏， 姚 沛， 高 惠

(1.石家庄职业技术学院 经济贸易系，河北 石家庄 050081；2.石家庄信息工程职业学院 国际贸易系，河北 石家庄 050035)



形象认识微积分

王玉苏1， 姚 沛2， 高 惠1

(1.石家庄职业技术学院 经济贸易系，河北 石家庄 050081；2.石家庄信息工程职业学院 国际贸易系，河北 石家庄 050035)

微积分是高职数学的重要组成部分，一般教科书中，微积分概念比较抽象，学生难以理解.用常见的动画解释什么是微积分，并给出微积分在各自领域的应用，能让学生在体验微积分乐趣和奥妙的同时，习惯用微积分来思考问题.

微分；积分；动画

微积分是高等数学中研究函数“微分”“积分”以及有关概念和应用的数学分支，同时也是高职数学的重要组成部分.在信息科技高度发达的今天，日常生活和社会经济活动中常常用到微积分，如银行存款、交通信息、股票价格分析等，凡针对各种微观变化与宏观变化的研究均离不开微积分.然而，微积分在大多数高职学生的印象中是“很难学的东西”和“没有用的东西”.这是因为微积分的某些概念比较抽象，甚至难以理解，对于刚进大学校门的高职学生，在学习中会感到不适应，常常出现畏难情绪，甚至不求甚解.本文从形象认识微积分入手，意在使学生在学习高等数学时轻松地理解微积分，体会微积分的思考方式和乐趣所在.

1 从动画看什么是微积分

手绘动画是由动画师用笔在专业的、透明度高的纸上绘制的，多张图纸拍成胶片放入电影机即可制作出动画片.它的特点是每张图片间有微小的逐渐变化的动作，当以每分钟几十张图片的速度播放时，画面就会动起来.

手绘动画的绘制与播放过程就体现了微积分的奥秘.如图片1和图片2是两张连续的图片，两张图片中青蛙在动作上就有微小的变化.

图1 体现微小变化的图片1

图2 体现微小变化的图片2

观察事物之间的微小变化就是微分.通俗地说，观察(寻找)函数相邻两点之间的微小变化就叫做函数的微分.

把一些具有微小变化的图片一张一张连续播放就构成完整的动画.这种把函数的每一个微小变化积累起来的过程，就是函数的积分.

2 函数的微分及作用

正如上文所说，观察函数相邻两点之间的微小变化就叫做函数的微分.

在动画中，有些动画相邻两张差别很小，反映到画面上，其动作变化的幅度较小；有些动画相邻两张差别相对较大，反映到画面上，其动作变化的幅度就大.如果把动画看作函数，函数相近的两点变化很小，说明其增长(下降)速度就小；函数相近的两点变化较大，说明其增长(下降)速度就大.

在很多实际问题中，凡要研究变量的快慢程度，如研究物体的运动速度，研究工农业总产值的增长速度等都需要用到微积分.在经济科学理论及经济活动的分析和决策中，对于一些主要的经济量之间的相关关系的研究也要用到微分学，如大量常规的经济分析涉及到个人、企业和政府试图追求最大化或最小化某种事物的活动，消费者在消费时试图使其总效用最大，企业试图在决策时使其利润最大(或使其损失最小)，政府要使国民就业水平达到最大(使失业最小)等等.

例1 某物体的运动轨迹为S(t)=t2+2t,其中，t为时间.求物体第7 s末和第8 s末的瞬时速度.

求物体的瞬时速度，可利用微分知识解决.

解 求路程函数对时间t的导数，即

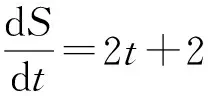
故物体第7 s末的速度为16 m/s，物体第8 s末的速度为18 m/s.

可以看到，第8 s末物体的运行速度大于第7 s末物体的运行速度.

例2 现有需求函数p=10-0.001q，总收益函数为R=pq=10q-0.001q2，总成本函数为C=100+7q+0.002q2.其中p为价格，q为产量，求总产量为多少时总利润最大.

解 总利润=总收入-总成本，

即L=(10q-0.001q2)-(100+7q+0.002q2)，化简得

L=3q-0.003q2-100.

其中，L表示总利润.

为了达到利润最大化，也可以利用微分知识解决.

即3-0.006q=0.

即在每一时期，产量为500单位时，利润函数具有最大值.

3 函数的积分及作用

积分是从微小个体出发来解决整体问题的.就如动画片，由一张张有微小变化的图片通过拍摄、连续播放，组成一部完整的动画.通俗地说，要研究某个事物，但这个事物的全貌一时看不清楚，我们采取的方法是，将这个事物分割成若干个小个体，分析每个小个体的特性，因为它小，容易看清楚.然后把每个小个体的特性积累起来，组成这个事物的整体容貌.这个过程在数学上就叫做积分.

积分学可以求平面上不规则区域的面积，度量曲线的长度，以及求任意空间物体的体积和质量.同时它也可以解决经济活动中一些经济量的关系问题.

如，求两条抛物线y2=x,y=x2，所围成的图形的面积.示意图见图3.

图3 y2=x,y=x2所围成的图形的面积示意

用积分的方法求阴影部分面积为：

再如，某产品的边际成本函数为C′(x)=2x+36，固定成本为500元，其中x为件数.

求总成本函数，利用积分的方法可以解决.

求边际成本的积分.

通过上述对微积分的形象解释，可使学生对微积分产生简单的、形象的基本认识.微积分不仅仅有大量的公式和理论推导过程，其思考问题的方法独特、简单，能切实可行地解决实际问题.

[1]平野叶一.微积分超入门.上海：世界图书出版公司，2005:1.

责任编辑：金 欣

A cognitive approach to the calculus using animation

WANG Yu-su1， YAO Pei2， GAO Hui1

(1.Department of Economics and Trade，Shijiazhuang Vocational Technology Institute，Shijiazhuang，Hebei 050081，China;2.Department of International Trade，Shijiazhuang Vocational Institute of Information Technology，Shijiazhuang，Hebei 050035，China)

Calculus is an essential part of mathematics in vocational colleges as a general subject.Therefore，this paper argues for animation mode in the instruction for the students to find the miracles of calculus.

differential; integral; animation

2015-09-24

王玉苏(1961-)，女，河北丰润人，石家庄职业技术学院教授.

1009-4873(2015)06-0059-03

O172

A