化学解题中假设的方法与技巧
2015-03-03归立厂
归立厂
(河北省怀来县沙城中学)
假设是科学研究中常用的一种思维方法,也是化学解题中常用的技巧和策略,在创造性思维活动中占有重要地位。本文举例谈谈化学解题中常用的假设方法与技巧。
一、极端假设
极端法是化学计算中的技巧性解法,它适用于混合物的计算。这种方法的解题思路是假设只有混合物中的某一成分,通过计算得出两个极端值,然后根据题目要求得出正确答案。
例1.Mg,Fe,Al 三种金属的混合物与足量的稀H2SO4反应,生成标准状况下的2.8L 的H2,则金属混合物中三种金属的物质的量之和不可能的是 ( )
A.0.12mol B.0.15mol
C.0.08mol D.0.10mol
【分析】物质的量相等的金属与足量的酸反应时产生H2的量只与金属元素的化合价有关,而已知的三种金属Mg,Al,Fe,其中Mg,Fe 在反应中均呈现+2 价,可把它们都看成一种成分,Al 在反应中呈现+3 价,把它看成另一种成分。则把该混合物转化成+2价的金属和+3 价的金属组成的混合物,然后用极端法来计算和判断。
解:假设全部是Mg,Fe,设它们的物质的量之和为xmol,与产生的H2有如下关系:

假设全是Al,设它的物质的量为ymol,与产生的H2关系为:

由于是以上两种情况的混合物,故产生2.8L 的H2时的混合物的物质的量之和应介于两者之间,即小于0.125mol 而大于0.08mol,故符合题意的答案为(B)和(C)。
极端法假设解题可以给化学计算带来极大的方便。利用这种方法解题时,应注意有的答案包括了两极端值,而有的答案则不包括两极端值,这要根据题意灵活判断。
二、中值假设
和极端假设相反,中值假设是选定变化过程中某点(如恰好反应点等)的量值为参照,或假设结果为某一中间值,代入原题中,通过分析、推理,然后对结果做出正确判断。尤其是对于某些结果为比值或含量的计算型选择题比较方便。
例2.已知自然界中铱有两种质量数分别为191 和193 的同位素,而铱的平均原子量为192.22,这两种同位素的原子个数比应为( )。
A.39:61 B.61:39
C.1:1 D.39:11
【分析】本题一般用十字交叉法求解,解题中会遇到十分难以处理的数据运算。用选值假设,假设比为1:1,则铱元素的平均原子量为说明两种原子中193 的原子个数要多于191 的原子个数,比值要小于1:1,对照选项可知只能选A。
三、过程假设
过程假设即把实际较为复杂的变化过程假设为若干个简单、理想的过程,并以其为参照,使问题变得简捷明了,并得以解决。
例3.在一密闭容器中充入1molNO2,建立如下平衡:2NO2葑N2O4,测得NO2的转化率为a%,在其他条件不变下,再充入1mol NO2,待新平衡建立时,又测得NO2的转化率为b%,则a 与b 的关系为( )
A.a>b B.a C.a=b D.无法确定 【分析】直接判断a 与b 的关系比较难,但可以假设一个中间过程Ⅱ。 易知Ⅰ与Ⅱ两过程等效,NO2的转化率均为a%,若将容器Ⅱ加压,使容积减小到原来的一半,即与Ⅰ容积相等,因2NO2葑N2O4,加压时平衡向正反应方向移动,故达新平衡后NO2的转化率b%必大于a%。答案应选B。 某些问题直接求解非常繁琐,甚至无法求解,解题中我们可通过对题所给条件进行假设,使问题研究的方向、结论等发生改变,从侧面或反向着手分析问题。 例4.将50%的硫酸溶液和10%的硫酸溶液等体积混合,所得溶液的质量分数( ) A.大于30% B.小于30% C.等于30% D.无法判断 【分析】假设50%和10%两硫酸溶液密度分别为d1和d2,并将它们等质量(均为m)混合,所得溶液质量分数为: 因为d1>d2,所以,两溶液等体积混合时,50%硫酸溶液的质量必大于10%硫酸溶液的质量,混合后溶液质量分数必大于30%,故(A)为答案。 所谓赋值假设,就是在无数据计算、字母讨论及以比值形式作已知条件或求比值的问题中,抓住特点(如,反应系数、比值等),赋予其一些具体的量值,化抽象为具体,使问题顺利解决。 例5.向碘化钾溶液中加入硝酸银溶液,直到完全反应为止,结果反应后,溶液的质量恰好等于反应前碘化钾溶液的质量,则加入硝酸银溶液的质量百分浓度为__________________。 【分析】由反应式KI+AgNO3=AgI+KNO3可知,析出碘化银沉淀的质量等于所加入硝酸银溶液的总质量,赋值假设有1mol 碘化银沉淀生成,则所加入的硝酸银溶液中含AgNO3为1mol,每摩AgNO3质量为170g,每摩AgI 的质量为235g,则所求硝酸银溶液的质量百分浓度为170÷235×100%=72.34%。本题原无明显可用数据,通过赋值假设,可以正确求解。 以上列举了化学解题中常用的几种假设方法与技巧,它不仅是快速解题的需要,同时对培养创造性思维能力也大有帮助。在解题时,应根据实际问题的具体条件进行灵活掌握,使假设的方法合理而又恰到好处,不必囿于一定模式,这样才能使思维水平得以发展,逐步形成解题技能和技巧。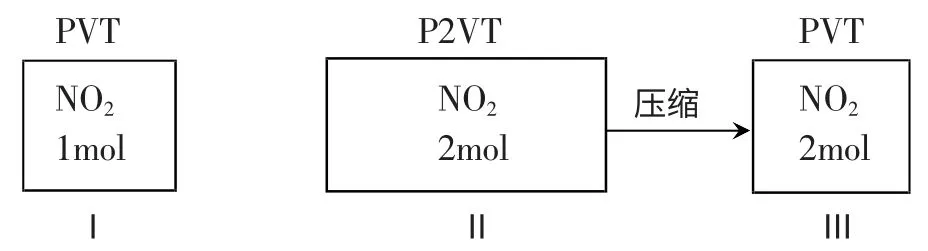
四、转向假设
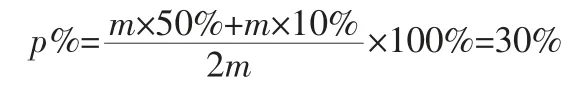
五、赋值假设
