由一道对数不等式所引发的讨论——少教多学案例
2015-03-03杨福海
杨福海
(福建省厦门第六中学)
课堂教学改革一直是教育改革中备受关注的主题。一方面,课堂教学是我国中小学教育活动中最基本构成部分,是中小学生在学校生活的主体部分,是中小学生素质发展的主要渠道,其重要性不言而喻;另一方面,课堂教学改革涉及教育问题的方方面面,它不仅要改变教师根深蒂固的传统教育观念,同时还要改变教师习以为常的教学行为、教学方式乃至生活方式,其艰难性不言而喻。
著名的教育学家夸美纽斯在他的《大教学论》中有这样的表述:“找出一种教育方法,使教师因此可以少教,而学生却可以多学;使学校因此少些喧嚣,厌恶和无益的劳苦,独具闲暇、快乐及坚实的进步。”这种教育思想一直以来都是教育工作者的追求,特别是新课程实施以来,我们每一位教师都想能够实现“少教多学”。
我校从2013 年起进行“少教多学”教学模式的探索,强调不拘形式,重在过程。在学习复合函数的单调性这节课中,我课前导学案布置了一道不等式:若logm2>logn2>0 时,则m,n 的大小关系是______。本想学生很快就能解决此问题,结果出乎意料地用了近20 分钟的时间讨论这道题,也让我再次深深体会了学习一定要从学生的角度来研究,而不能主观地以定式思维出发。
少教多学提倡学生多交流,多展示。因此上课的第一件事就是让学生把昨晚预习的作业进行展示和交流。在展示预习作业的过程中,雪婷同学认为通过作图能得到m,n 的大小关系,于是到黑板上画了图1 这样的图形,然后说“根据对数函数的图象与性质,当底数大于1 时,底数越大,图象越接近x 轴,从而得到n>m。”我们一般在学生展示完后要接受同学的提问和老师的点评,于是就有同学提出疑问:为什么图象是单调递增的?雪婷同学回答:Qlogm2>0 即logm2>logm1∴y=logmx 单调递增。在回答的过程中,雪婷同学发现了自己所画的图象边上的不应该写式子logm2,于是赶紧改为y=logmx 和y=lognx。这告诉我们一个道理,交流使人进步。雪婷同学话音刚落,又有同学提出能否借助直线y=1 与图象的交点,如图2 更能直观地判断n>m,理由是logmm=lognn=1。

图1
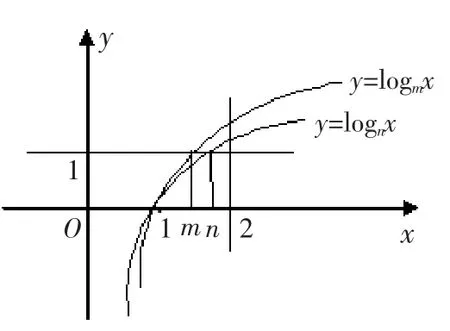
图2
我肯定了这个同学的想法,请各小组交流两种判断方法的异同。一小组的同学总结说:两个同学相同之处都是借助了对数函数的图象;第二个同学的方法适用于任何一个对数函数的图象比较底数的大小,更加直观易理解,第一个同学掌握并运用了对数函数的性质,就是要注意区分底数大于1 还是小于1。到此,很多同学都以为问题已经解决了。可又有一组同学在交流过程中提出了另一个想法:用赋值法不是更简单吗?令m=2,n=4,满足logm2>logn2>0,从而说明n>m。同学们给予了掌声。这时我提出了疑问,怎么保证没有别的可能性呢?再交流。过后国荐同学补充赋值的依据,m,n>1 且m≠n,因此只有n>m 或n<m 两种情况。再令m=4,n=2 不成立,所以n>m。我顺着这位同学的发言再次提出思考,还有什么方法可以比较两个对数的大小?再交流(我这里特意强调比较两个对数的大小),很快有小组心领神会,子隽同学回答:化同底,看单调。于是∴m<n。显然,这里利用了logm2·log2m=1 的运算性质。但同时也提出了一个问题,能否得到log2m<log2n,通过交流,欣瑜同学回答,分母大的倒数反而小,另一组有同学提问,如果一个负数一个正数就不符合了。再一组同学补充说把化为log2m<log2n,两边同乘以log2m·log2n,只有同号时方向才不变,因此只要同号,分母大的就反而小。此时学生又收获了除对数运算性质外的另一个不等式的性质,话音刚落,又有一组同学周臻说,也可以利用换底公式转化为,更容易看出lgm<lgn,从而1<m<n,(此时又复习了一个运算性质)。我看看花了不少时间了,想要结束此话题了,不想又有一个女生说,她们组还有一种解法,设logm2=x1,logn2=x2,则,即。又∵y=2x单调递增,。真是出人意料。竟然也可利用对数式与指数式的互换,利用指数函数的单调性解决问题。这与利用对数函数的单调性有异曲同工之效果。
看着同学们对问题讨论兴趣的高昂,我再次抛出一个新的问题:若将此题改为已知logm2>logn2,比较m,n 的大小?让学生课后再做思考。
本节课本来的主题是复合函数的单调性,却没想到一道复习引入题引起这么多的讨论与解决方法。虽然本节课还留下一些问题没有解决,但让我感受到了少教多学的乐趣,感受到了同学们之间交流的重要意义,更感受到了不一样的思维方式。教师在教学过程中要注意分层教学,对待不同的学生,采取不同的教学方法,使得学生的弱点和缺陷得到强化提高,从而保证了学生的学习质量。
“少教多学”是对传统教学的颠覆,是一种教学模式的创新。其实,“少教多学”也并非是一种全新的事物,在教学的某些环节上或不同的课型上,例如习题课和例题教学上,一般都采用少教多学的方法。但是,创新是对原有方法或关系的变革与调整,而不是彻底否决,因此创新一定要有所继承,没有继承的创新好比无源之水,其生命力是不会长久的。从理论来看,新旧迁移是构建知识的基本形式;从实际来看,学生的学习水平与知识状况不是在同一水平线上的,而且知识内化成认知结构需要一个不断重复强化的过程,事实也正是这样,因为缺少必要的预备与介入,一部分学生学习上困难重重,造成了学习上的退步。这才要求我们提倡“少教多学”,使学生理解并参与“少教多学”的探索,并落实到实处,在预习与展示和交流过程中发现问题、当堂解决问题,同时巩固所学知识,树立自强、自立、自信的理念。
