基于M/M/c/∞排队模型分析超市收银台数量
2015-03-03王颖俐
王颖俐
(长治学院 数学系,山西 长治 046011)
基于M/M/c/∞排队模型分析超市收银台数量
王颖俐
(长治学院 数学系,山西 长治 046011)
介绍排队论在处理超市收银服务的基本理论,并在此基础上应用M/M/c/∞排队模型对某一超市排队现象进行研究.通过收集、整理数据,并对来客量进行K-S泊松检验,进而得到超市的一些相关指标,最终得到该超市的最优收银台数目.
超市;收银台数量;M/M/c/∞排队模型;K-S检验
超市的来客流量是一个随多种因素变化的量,收银台的配备及开启量决定超市的运行成本和效益,现阶段许多学者解决这一问题的方法是将系统中的由于等待所产生的损失费用加上超市开放收费窗口的费用作为总费用,进而构造各种模型使得这个费用最小的窗口数即为所求[1-4].超市收银系统是一个动态的多服务台等待制的随机服务系统,但是已有这些模型因静态性、确定性而限制了其适用性.
基于以上考虑,本文引入M/M/c/∞排队模型对该问题进行研究.首先在收集客流量数据的基础上,运用SPSS统计软件对该数据进行K-S单样本检验其是否服从泊松到达,进而套用排队理论得到超市的一些相关指标,最终得到得到该超市的最优收银台数目.由结论分析超市的收银台配备的合理性,对超市管理者具有一定的参考价值.
1 M/M/c/∞排队模型
我们考虑一个多服务单到达的排队系统M/M/c/∞[5],运行规则如下:
顾客以参数为λ(λ>0)的速率泊松到达,λ>0为顾客到达强度,即单位时间内的顾客平均到达量.当顾客到达服务台时,若空闲,则立即接受服务;否则排队等待,直到服务台空闲再接受服务.服务原则遵循先到先服务.
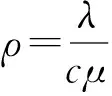
假定N(t)表示在时刻t时系统中的顾客总数,令Pij(Δt)=P(N(t+Δt)=j|N(t)=i),则有:
Pi,j(Δt)=o(Δt),|i-j|≥2;
Pi,i+1(Δt)=λ·Δt+o(Δt);
Pi,i-1(Δt)=iμ·Δt+o(Δt),i≤c;
Pi,i-1(Δt)=cμ·Δt+o(Δt),i>c;
Pi,i(Δt)=1-(λ+iμ)Δt+o(Δt).
于是{N(t),t≥0}为状态集S={0,1,2,…}上的生灭过程[6].
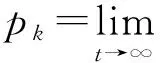
特别地,当只有一个服务台时,系统变为M/M/1/∞,且有
在统计平衡下,当ρc<1时,等待队长Lq的期望值为:
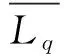
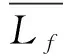
假设Wq为等待服务时间,T为逗留时间,则由Little公式[6]有:
由于系统中有c个并行服务台,则在ρc<1时,到达服务台的顾客需等待的概率为:
2 模型应用
K-S检验[7]是以两位苏联数学家Kolmogorov和Smirnov的名字命名的,是一种非参数检验,也是一种拟合优度检验,可以通过对两个分布之间的差异的分析,由样本数据推断出总体是否服从某一理论分布.
以某镇超市进行分析,对该超市索取了为期100 d的客流量统计数据,通过SPSS统计软件进行单样本K-S检验,验证顾客到达是否服从泊松分布,表1为输出结果.

表1 单样本Kolmogorov-Smirnov检验
a.检验分布为Poisson分布.b.根据数据计算得到.
由表1知,显著性水平P=0.968>0.05,可得每日客流量服从泊松分布.又知超市配有6个收银台,但平时只启动4个,则超市收银台系统可看做M/M/c/∞排队系统,对客流量绘制曲线图可得图1.
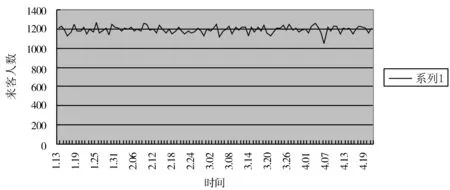
图1 来客流量图
对该数据还可得到如表2所示的各统计量的值.

表2 描述性统计量

由以上数据可得,该超市需配备的服务台数应在(1.438 1,4.561 5)区间,服务时间应控制在(0.238 5,2.780 3)区间中.当超市开启4个服务台时,每位顾客的平均逗留时间是1.509 4 min,必须等待的概率为0.314 6,因此在超市提供4个服务台时,可满足顾客结账需求,所以设置6个服务台有点浪费成本.若为节约成本,当超市尝试开启3个服务台时,顾客平均逗留时间为2.930 7 min,必须等待的概率为0.693 5.这样虽然会使得顾客等待时间变长,但也影响不大,所以超市可尝试使用3个服务台,同时在特殊节日时增加到4个甚至5个服务台,以满足最大的客流量.因此从以上的分析中可知该超市的收款台数量的设置是相对合理的,但排队模型所假定的平稳性一定程度上限制了其对现实的适应性,这是今后对该模型改善的一个方向,另外,超市也可对顾客购买的数量进行区分通道结账,这也是对该模型改善的另一个方向.
[1] 彭志捌,张 凤.超市服务台与人员配备模型设计[J].长沙大学学报,2004,18(4):65-67
[2] 郑 欢,古福文.大型超市顾客交费排队系统优化分析[J].管理学报,2005,2(2):171-173
[3] 蒋淑华,伏小良.基于排队论的超市收费服务模型的探讨[J].物流科技,2008(10):141-142
[4] 李娜等.考虑顾客体验的排队系统研究[J].工业工程与管理,2012,17(3):36-41
[5] 孙荣恒,李建平.排队论基础[M].北京:科学出版社,2001
[6] 方兆本,缪柏其.随机过程(第三版)[M].北京:科学出版社,2011
[7] 李裕奇,等.非参数统计方法[M].成都:西南交通大学出版社,2010
Analysis the Supermarket Casher Number Based on theM/M/c/∞Queuing Model
Wang Yingli
(The Department of Mathematics, Changzhi College, Changzhi 046011, China)
To deal with the supermarket queuing phenomenon, this paper studies the queuing model for the basic theory of supermarket cash register service. Through the collecting, sorting data, we use SPSS software to poisson test of traffic, get some index of the supermarket, and then get the optimal number of the supermarket checkout.
supermarket; casher number;M/M/c/∞queuing model; K-S test
2015-05-22
长治学院课题项目(201412).
王颖俐(1987-),女,山西临汾人,硕士,长治学院数学系讲师,主要从事时间序列分析及排队论等领域的研究.
1672-2027(2015)02-0008-03
O226
A
