PO+MEC计算目标近场电磁散射特性

张京国， 金桂玉， 高　宠

(中国空空导弹研究院， 河南 洛阳　471009)



PO+MEC计算目标近场电磁散射特性

张京国， 金桂玉， 高宠

(中国空空导弹研究院， 河南 洛阳471009)

摘要：基于面元法思想， 将目标表面近似为面元和棱边的组合， 再用物理光学法(PO)、 等效电磁流法(MEC)等高频近似解法分别计算面元散射场和边缘绕射场， 经矢量叠加求得目标总体近场电磁散射特性。 计算程序区分了凹凸棱边， 并在比较了多种不同等效电磁流表达式之后， 选择了一种既能很好地减少绕射场计算奇异点， 又使计算结果更加符合实际情况的表达式。 最后以某隐身飞机为例， 计算了复杂目标近场RCS。

关键词：雷达散射截面； 物理光学法； 等效电磁流法

0引言

目标电磁散射特性预估是雷达探测与识别、 隐身与反隐身等技术的重要基础。 传统意义的雷达散射截面定义在远场、 近场条件下雷达与目标之间的距离与探测波长的关系已不能满足远场条件， 目标本身被看作体目标， 不但结构和散射机理复杂， 而且不同部位与接收机天线之间的距离变化较大， 目标形状、 交会角等都会对散射回波产生重要影响。 目前， 对于目标近场电磁散射特性计算问题， 在理论上还没有严格的解析计算方法。

本文用面元法实现目标近场RCS近似计算， 对于形状规则、 可求出其精确解析解的目标， 其RCS计算结果与精确解基本一致； 对于可测量的电大尺寸复杂目标， 其RCS计算结果与测量结果基本一致。

1三角面元划分

目标模型的绘制可借助AutoCAD，CATIA，UG，Pro/E等三维建模软件。 完成目标模型构建之后， 首先将其拆分为三角形面元的组合。 这里以球体为例对面元划分过程进行简述。 设球体半径r=0.25m； 入射波长λ=5cm， 划分三角形面元时以1/3波长作为面元最大线尺寸， 则面元个数N满足

(1)

式中： N≥6 530。

2PO法计算面元散射场

2.1　遮挡判别

PO计算过程仅考虑目标表面被照射部分， 计算前需进行遮挡判别。 目标表面数据结构如图1所示， 面元法向量与散射方向单位向量之间的夹角小于90°时， 计算其RCS， 反之认为面元被遮挡。

图1　目标表面数据结构

2.2　PO计算多边形平板散射场

多边形平板单站/双站RCS平方根表达式如下[1]：

(2)

当T=0即ω在平板上分量为零时， 式(2)中的积分可简化为多边形平板的面积：

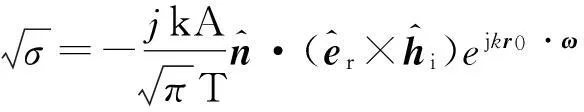
(3)

式中：A为多边形平板的面积。

3MEC法计算边缘绕射场

3.1　棱边识别

图2　劈边缘几何结构及绕射情况

对于劈边缘的识别可分为以下三步：

(1)公共点判别：采用循环查询方式依次比较两个三角形面元的顶点， 存在两个公共端点时， 转入步骤(2)；

(3)凸凹判别：以相邻两个三角形中任意一个为基准建立局部坐标系， 求出另一个三角形除公共端点以外的第三个点在该局部坐标系下的坐标值， 若该坐标值中Z值为负则满足劈边缘条件， 否则视为二面角不计算其绕射场。

3.2　绕射场计算

为解决MEC法的奇异性问题， 相关学者做了大量工作， 分别以不同方式对等效电磁流表达式中的参数进行补充和修正， 如国外学者Michaeli， Mitzner， Ando等人和国内学者崔所民、 吴振森、 张民、 徐云学、 赵维江等人。 但目前为止既能保证算法的合理性又能完全消除MEC奇异点的算法或绕射系数的表达式仍未出现， 只能在结果误差允许范围内尽可能少地减少表达式的奇异性。

其中应用较广的是Michaeli提出的PTD-EEC[2]和Mitzner提出的ILDC[3]。 两者都从总场中减去物理光学场的贡献， 但具有不同的绕射场计算结果， 绕射线方向偏离劈面内垂直于劈边缘的方向越远， 两者差别就越大。

ILDC在阴影和反射边界上都具有良好的属性， 但在特定观察方向上仍具有奇异性[2-3]； PTD-EEC虽消除了ILDC中的一些奇异性， 但当劈边缘绕射线方向与劈面内垂直边缘方向偏离较远时， 结果不够准确。 本文采用文献[4]中改进的MEC表达式计算劈边缘绕射场， 计算结果真实可信且有很强的实用性。

根据文献[5]， ILDC与Michaeli最初提出的用于计算总场散射的GTD-EEC相比， 区别只在于物理光学绕射系数的修正， 因此这里用等效电磁流形式给出ILDC的表达式。 根据文献[6]， 等效线电流Ie和等效线磁流Im可分解为如下形式：

(4)

式中：I1，I2分别为两个劈面上的表面线电流；M1，M2分别为两个劈面上的表面线磁流。 求得I1，M1之后， 可经过如下转换得到劈面2对应的I2和M2：

(5)

由文献[2]知，I1和M1代表总的电磁场， 可分解为物理光学场和边缘绕射场：

(6)

(7)

(8)

(9)

(10)

(11)

根据式(4)得到如下表达式可计算出整个劈边缘的绕射场：

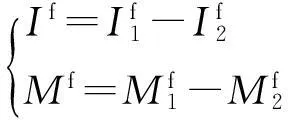
(12)

sinβscosφs=±sinβi

(13)

或

(14)

(15)

当散射方向在这两个锥上时， 上述ILDC计算出现奇异性。

cosγ=sinβisinβscosφs+cosβicosβs

(16)

(17)

(18)

cosγ=sinβsinβscosφs+cosβcosβs

(19)

(20)

4总RCS计算

假设目标模型由M个小面元和N个尖劈单元组成， 其近场总体RCS为

(21)

5计算结果分析

首先以5λ×5λ(λ=0.032m)的正方形平板为例对其RCS进行求解， 所得计算结果与文献[10]中实际测量结果趋于一致， 如图3所示。

图3　5λ×5λ平板RCS结果

以同样的方法计算无涂覆材料时某隐身飞机的RCS， 计算结果如图4所示。 该型隐身飞机交会过程的RCS仿真结果见图5。 弹目交会过程的RCS曲线急剧起伏， 对引信探测来说， 弹目交会过程的RCS曲线更具实际意义。

图4　某隐身飞机近场RCS仿真结果(距离20 m处)

图5　某隐身飞机迎头交会过程RCS(距离9 m处)

参考文献：

[1] 阮颖铮．雷达截面与隐身技术[M]．北京：国防工业出版社， 1998： 30-135．

[2] Michaeli A．Elimination of Infinities in Equivalent Edge Currents, Part I： Fringe Current Components[J]．IEEE Transactions on Antennas and Propagation， 1986， 34(7)： 912-918．

[3] Mitzner K M．Incremental Length Diffraction Coefficients[R]．Northrop Corp Hawthorne CA Aircraft Div, AD0918861, 1974．

[4] 赵维江．复杂目标雷达截面计算方法研究[D]．西安： 西安电子科技大学， 1999.

[5] Knott E F．The Relationship Between Mitzner’s ILDC and Michaeli’s Equivalent Currents[J]．IEEE Transactions on Antennas and Propagation， 1985， 33(1)： 112-114．

[6] Michaeli A．Equivalent Edge Currents for Arbitrary Aspect of Observation[J]．IEEE Transactions on Antennas and Propagation， 1984， 32(3)： 252-258．

[7] 赵维江， 龚书喜， 刘其中．一种新的等效电磁流边缘分量表达式[J]．电子学报， 2002， 30(9)： 1340-1343．

[8] Kouyoumjian R G， Pathak P H．An Uniform Geometrical Theory of Diffraction for an Edge in a Perfectly Conducting Surface[J]．Proceedings of the IEEE， 1974， 62(11)： 1448-1461．

[9] Knott E F， Senior T B A．Equivalent Currents for a Ring Discontinuity[J]．IEEE Transactions on Antennas and Propagation， 1973， 21(5)： 693-695．

[10] Ross R A．Radar Cross Section of Rectangular Flat Plate as a Function of Aspect Angle[J]．IEEE Transactions on Antennas and Propagation， 1996， 14(3)： 325-339．

Computing Targets’ Near-Field Electromagnetic Scattering

Characteristics Using PO and MEC

Zhang Jingguo, Jin Guiyu, Gao Chong

(China Airborne Missile Academy, Luoyang 471009, China)

Abstract:The target could be represented as a combination of facets and edges based on faceting approach. Physical optics (PO)method is adopted to calculate the facet’s scattered field and the method of equivalent currents(MEC) is used to calculate the edge diffraction. Taking facet contribution and edge diffraction into consideration, this paper gets the total scattering field by vector superposition. Besides, dihedral angle and raised edge are distinguished in the process. After comparing several different MEC expressions, an expression which can not only reduce the extreme point in edge diffraction calculation, but also make the results be more in line with the actual situation. At last, taking the stealth aircraft as an example, complex targets’ near-field RCS are gotten.

Key words:RCS； PO； MEC

作者简介：张京国(1966-)，男，河南洛阳人，博士，研究方向为目标与环境特性、引战配合。

收稿日期：2015-07-30

中图分类号：TN011

文献标识码：A

文章编号：1673-5048(2015)06-0031-05