脉冲多普勒引信海面回波建模与仿真

吴万芳 ， 杨　硕， 刘建新

(1.中国空空导弹研究院， 河南 洛阳　471009; 2.驻中国空空导弹研究院军事代表室， 河南 洛阳　471009)



脉冲多普勒引信海面回波建模与仿真

吴万芳1， 杨硕2， 刘建新1

(1.中国空空导弹研究院， 河南 洛阳471009; 2.驻中国空空导弹研究院军事代表室， 河南 洛阳471009)

摘要：脉冲多普勒引信海面回波仿真是根据无线电脉冲多普勒引信的探测特点和海面反射特性划分海面有效照射区域的等距离线, 并由导弹飞行姿态和引信天线波束宽度确定海面有效照射区的等多普勒线。 利用雷达方程进行建模仿真,对回波能量进行积分得到引信回波功率， 对照射面元回波累加得到多普勒回波信号,从而为研究脉冲多普勒引信海面低空工作性能提供参考。

关键词：无线电引信; 海面回波; 多普勒回波

0引言

导弹在进行掠海低空、 超低空飞行时， 引信不仅能够探测到目标的回波信号， 也会探测到不需要的海面回波信号。 如何满足无线电引信超低空作战性能要求， 有效地在海面背景下探测目标， 是引战系统超低空作战领域的研究难点， 必须首先掌握引信海面背景的回波特征， 为消除或减小海杂波的影响提供理论依据。 为此本文分析计算了脉冲多普勒引信对海面的散射系数、 多普勒回波以及回波功率， 为引信超低空技术措施提供参考。

1海面后向散射系数计算模型

建立海面后向散射系数模型时所用到的导弹相对地面的几何关系如图1所示。

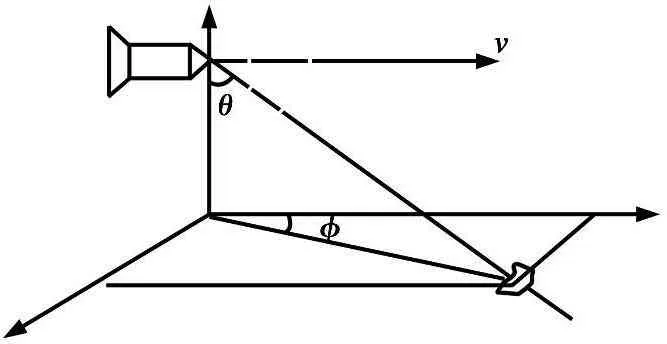
图1　导弹相对地面的几何关系

其中：θ为入射角；φ为入射方向在水平面上的投影与逆风方向的夹角。

海面后向散射系数可表示为

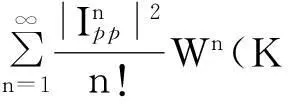
(1)

(2)

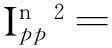
(3)

式中：k1为波数；K=k1sin(θ)；σ2为海面的高程差；W(kx,ky)为海面波谱， 即相关函数的傅立叶变换乘以σ2，Wn(kx,ky)为海面相关函数的n次方的傅立叶变换， 将Wn(kx,ky)写成极坐标的形式即式(1)中的Wn(K,φ)；fpp，Fpp与菲涅耳反射系数有关, 其定义参见有关文献。

由式(3)可以看出， 影响海面后向散射系数的因素有： 工作频率f、 入射角θ、 入射方向在水平面上的投影与逆风方向的夹角φ、 海温和海水的含盐量、 海面风速(海面风速决定了海面的波高谱、 高度起伏方差和海面的高阶谱)。

2海面杂波功率计算模型

当发射机、 接收机在同一位置， 且收、 发机共用同一副天线时， 实际海面背景雷达方程为

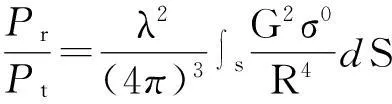
(4)

式中： σ0为后向散射系数； S为所有回波照射到的地面面积的并集。 本文海杂波计算模型的推导都建立在该雷达方程之上。

假设发射机发射功率Pt在发射时间内恒定不变， 则接收机在一个接收距离门内收到的平均功率应为收到的总回波能量除以距离门宽度， 即

(5)

首先计算多普勒频率为fd处的回波能量。 当导弹水平飞行时：

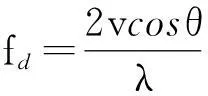
(6)

式中： v为导弹飞行速度。

取距离模糊数N， 则E(fd)的计算式为

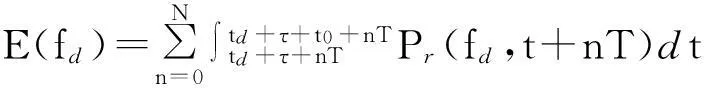
(7)

式中： Pr(fd,t+nT)为t时刻接收到、 距离门之前第n个周期内的脉冲发射的回波的功率, 如图2所示。

图2　发射脉冲和接收距离门的时间关系图

将式(7)带入式(5)并作归一化处理， 得

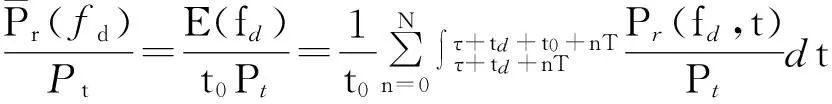
(8)

根据雷达方程， 可将式(8)改写为

(9)

式中：Gs为系统增益；Gm为子午面天线方向性系数；Ge为赤道面天线方向性系数；λ，Gs和h为常数，Gm由多普勒频率fd确定， 而Ge和σ则同r和φ有关。S(fd,t)为收到的回波相应的地面区域。 一般情况下， 该区域是发射脉冲前沿和后沿在地面上的两条等距离线与多普勒频移为fd-Δfd/2和fd+Δfd/2的两条等多普勒线围成的区域。 积分采用极坐标系， 面积微分dS可写为rdrdφ。

发射脉冲前沿在t时间内从发射机到地面再回到接收机所经历的路程为2Rmax， 发射脉冲后沿在t-τ时间内从发射机到地面再回到接收机所经历的路程为2Rmin， 如图3所示。

图3　等多普勒线与等距离线

图3中，h为导弹高度， 若发射脉冲的周期T足够短， 可以认为在N个周期内，h不变。

当r确定时， 对dφ的积分实际上是在半径为r的等距离线的一小段弧上的积分， 其积分上下限由多普勒频率分别为fd+Δfd/2和fd-Δfd/2的两条等多普勒线决定。 假设Δfd足够小， 可以认为在这段弧长上， 式(9)被积函数中的子午面天线方向图不变。

计算多普勒回波时把天线波束按赤道面和子午面分成许多的立体波束， 取立体波束照射到地面面元的中点作为参考点计算波束的入射角， 计算出该面元的回波电压信号为

式中： Z 为引信天线的输入阻抗； Prn为单个面元的功率。

对所有照射面元的回波信号矢量求和， 即海面时域多普勒回波信号为

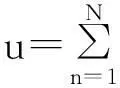
(10)

式中： Rn为地面面元到引信的距离。

3海洋表面后向散射系数计算模型验证

为验证海面散射模型的正确性， 采用实测数据与理论计算数据进行比较， 如图4~5所示。 图4是在工作频率14.6GHz、 海面风速7m/s的条件下， 测得的海面后向散射系数随入射角变化的情况， 数据包含VV和HH两种极化的海面后向散射系数。 结果显示， 在不同的入射角条件下， 模型均能够比较好地与试验数据吻合。

图4　散射系数计算与测量结果

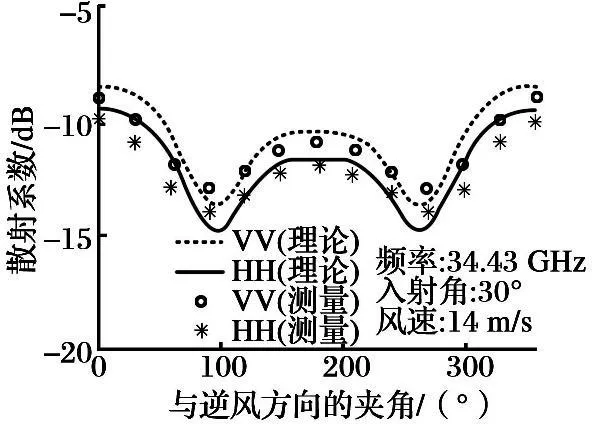
图5　散射系数计算与测量结果比较

图5是在工作频率为34.43 GHz， 入射角为30°， 海面风速为14 m/s 的条件下， 测得的海面后向散射系数随测量方向和逆风方向的夹角变化的情况， 数据包含VV和HH两种极化的海面后向散射系数。 结果显示， 在不同的测量方向和逆风方向的夹角的条件下， 模型均能够比较好地与试验数据吻合， 是一种比较适用的模型。

4海面功率计算结果

本文计算1, 3, 5级海情条件下某引信主通道第一距离副瓣处海面回波， 统计计算了不同海情回波功率随引信俯仰角的变化关系。 归一化回波功率随引信俯仰角的变化趋势如图6所示。

图6　归一化回波幅值随引信俯仰角的变化趋势

由图6可以看出， 引信俯仰角为25°时， 引信波束垂直于海平面， 各种海情主通道第一距离副瓣处回波功率最大， 该状态1级海情回波功率大于3级海情， 3级海情回波功率大于5级海情。 随着引信波束偏离垂直入射方向， 各海情回波幅度都减小， 低级海情的减小速率大于高级海情的减小速率， 在引信波束入射方向偏离垂直入射10°左右时， 5级海情的回波幅度超过了1级海情的回波幅度， 该状态5级海情回波幅度大于3级海情， 3级海情回波幅度大于1级海情。

5多普勒回波计算结果

经过计算， 得到了某微波引信1级海情海面回波的主通道多普勒回波信号和频谱图, 如图7~8所示。

图7　某引信脱靶量6 m俯冲角10°平飞多普勒回波

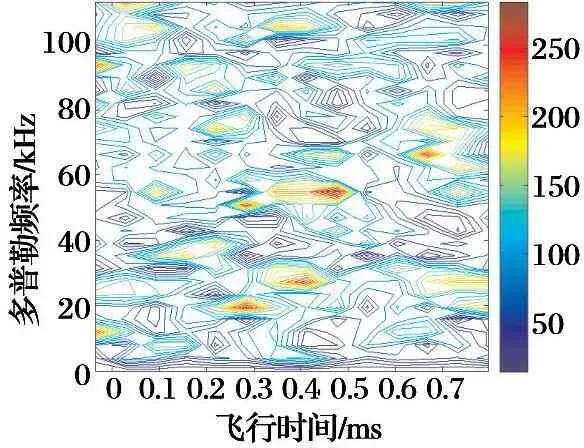
图8　某引信脱靶量6 m俯冲角10°频谱图

由计算结果可以看出， 引信对海面背景的多普勒频率分布较为分散， 不像对目标的多普勒频率相对集中， 利用频率从海面背景中区分目标的方法比较困难。

6结束语

引信的俯冲角、 海情以及引信自身的脉冲体制等都直接影响引信接收的海面回波的大小。 海面背景有较强的反射作用， 在距离副瓣内产生较强的海杂波干扰， 影响引信的低空作战能力。 本文结合无线电脉冲多普勒引信的探测特点和海面特性建立的脉冲多普勒引信海面回波计算模型,可有效地反映无线电脉冲多普勒引信的海面回波信号特征, 为无线电引信设计中对海面回波的抑制提供了依据。

参考文献：

[1] 周春花， 李冀刚. 无线电脉冲引信海面回波建模及仿真[J]. 制导与引信, 2010, 31(3):18-22.

[2] Guissard A, Baufays C, Sobieski P. Sea Surface Description Requirements for Electro-Magnetic Scattering Calculation[J].Journal of Geophysical Research Oceans,2012,9(2):2277-2492.

[3] Harunobu M, Ken’lchi O, Masanobu S, et al. Measurement of Microwave Backscattering Signatures of the Ocean Surface Using X Band and Ka Band Airborne Scatterometers[J].Journal of Geophysical Research Oceans,1986, 91(C11):13065-13083.

[4] Weissman D E. Dependence of the Microwave Radar Cross Section on Ocean Surface Variables[J]. Journal of Geophysical Research Oceans, 1990, 95(C3): 3387-3398.

[5] 袁正， 孙志杰. 空空导弹引战系统设计[M]. 北京： 国防工业出版社， 2007.

[6] Ulaby F T, Dobson M C. Handbook of Radar Scattering Statistics for Terrain[M]. Artech House, 1989.

Modeling and Simulation of Sea Echo of Pulse Doppler Fuze

Wu Wanfang1, Yang Shuo2, Liu Jianxin1

(1.China Airborne Missile Academy， Luoyang 471009， China;

2.PLA’s Military Representative Office in China Airborne Missile Academy, Luoyang 471009, China)

Abstract:The simulation of sea echo of pulse doppler fuze is the equal distance lines of dividing the sea surface effective radiation area, according to the detection characteristic of the pulse doppler radio fuze and the sea surface reflection characteristic.And the doppler isoline of sea surface effective radiatian area is determined by the missile flight pose and the fuze antenna irradiation wave width.Using the radar equation modeling, the echo energy is integrated to get the echo power, and the doppler echo is calculated by adding up the echo of surface elements. This provides a referene for researching the low sky working performance of the pulse doppler radio fuze.

Key words:radio fuze; sea echo; doppler echo

作者简介：吴万芳(1976-)， 女， 山东济南人， 高级工程师， 研究方向为目标与环境特性。

收稿日期：2015-07-30

中图分类号：TJ430.1

文献标识码：A

文章编号：1673-5048(2015)06-0066-04