基于土体小应变本构模型的TRD工法成墙试验数值模拟
2015-03-03徐中华王卫东
何 平 ,徐中华 ,王卫东 ,李 青
(1. 同济大学 土木工程学院,上海 200092;2. 同济大学 岩土及地下教育部重点实验室,上海 200092;3. 华东建筑设计研究总院 地基基础与地下工程设计研究中心,上海 200002;4. 华东建筑设计研究总院 上海基坑工程环境安全控制工程技术研究中心,上海 200002)
1 引 言
基坑开挖引起的土体变形主要发生在 3个阶段,即围护结构施工、基坑降水和基坑开挖。在传统的基坑有限元分析中,常忽略由围护结构施工引起的应力重分布和土体变形,实质上,在基坑开挖前成墙施工过程必然会改变土体的原始应力状态,引起土层发生侧向变形和地表沉降,这部分土体位移往往是不容忽视的。Schafer等[1]分析了正常固结黏土中地下连续墙成槽过程中的土压力扰动和土体变形,结果表明考虑成槽施工引起的基坑变形比传统的未考虑成槽施工影响要大10%~15%,因此有必要分析和研究成墙施工引起的土体变形,以便更为合理地预测基坑开挖对周围环境的影响。
TRD工法即等厚度水泥土搅拌墙技术,基本原理是利用链锯式刀具箱竖直插入地层中,然后作水平横向运动,同时由链条带动刀具作上下的回转运动,搅拌原土并灌入水泥浆,形成一定厚度的墙。目前等厚度水泥土搅拌墙在基坑工程中主要作为隔水帷幕或内插型钢形成复合隔水挡土结构。由于TRD工法设备切削能力强且具有连续成墙、厚度一致、墙体均匀性好等特点,近些年来在基坑工程中得到了广泛应用[2-4]。
本文以上海国际金融中心基坑工程开展的TRD工法搅拌墙成墙试验为背景,基于土体的小应变本构模型对其成墙过程进行了有限元模拟,得到了土体的侧向变形和地表沉降,并与监测结果进行了对比分析,针对不同深度的成墙进行了研究,并给出了TRD成墙引起的地表沉降包络线,可为预测TRD不同成墙深度引起的地表沉降和土体侧向位移提供依据。
2 TRD工法成墙试验简介
2.1 工程概况
上海国际金融中心项目位于上海市浦东新区竹林路以东,张家浜河以北。基坑开挖面积约为48 860 m2,开挖深度为26.5~28.06 m。
场地浅层以软弱的淤泥质粉质黏土、淤泥质黏土、粉质黏土为主,深层的第⑦、⑨层以砂质粉土、粉砂为主。场地内第⑦、⑨层为承压含水层,由于第⑧层黏性土缺失,因此第⑦、⑨层承压含水层连通。考虑到对承压水的控制,本工程在地下连续墙外围采用 TRD等厚度水泥土搅拌墙作为悬挂隔水帷幕,其深度达到56 m,基坑典型围护剖面如图1所示。
2.2 TRD工法试成墙过程与监测
为确定等厚度水泥土搅拌墙施工参数,现场开展了TRD工法试成墙试验。试成墙厚0.7 m、宽8 m、深56 m,实际开挖深度达到56.7 m。为了研究成墙施工对土体位移的影响,在施工前,布设了地表沉降监测点、土体深层水平位移监测点进行相应监测,监测点布置图如图2所示,具体监测结果见文献[5]。
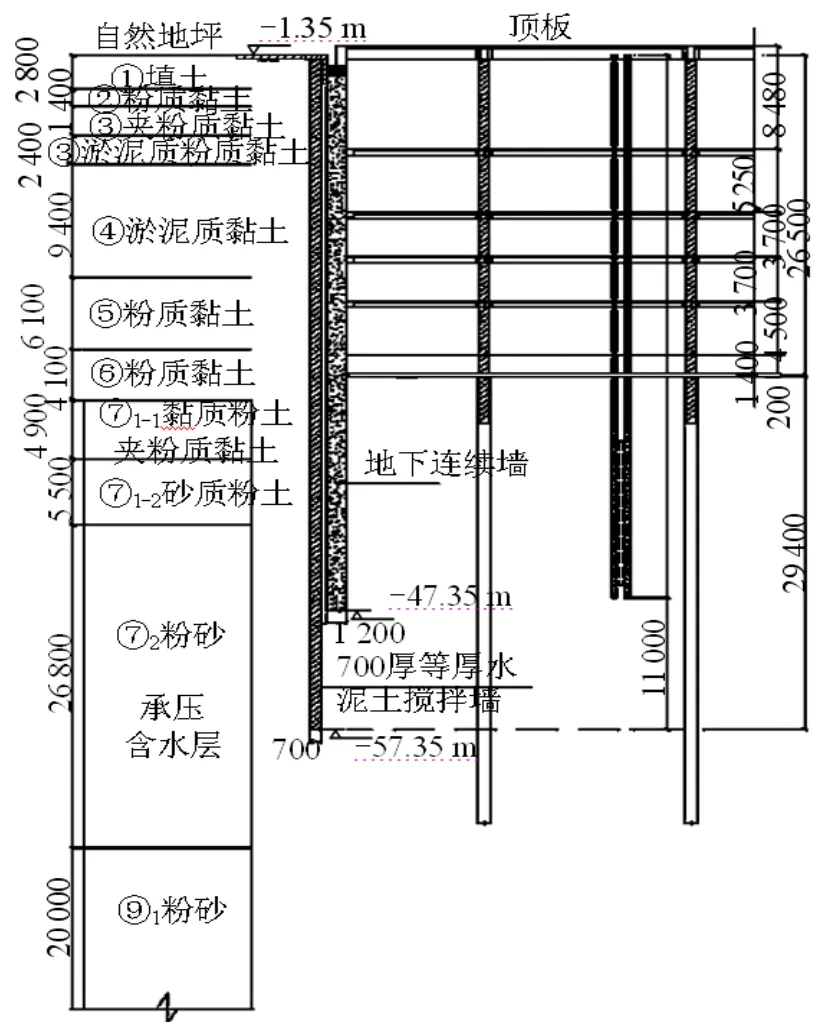
图1 基坑支护剖面图(单位: mm)Fig.1 Cross section of excavation supporting(unit: mm)

图2 试验监测点剖面布置(单位: mm)Fig.2 Layout of monitoring points(unit: mm)
3 TRD工法试成墙的有限元分析
3.1 计算模型
采用PLAXIS二维平面应变有限元对TRD成墙过程进行模拟,选用15节点三角形单元。虽然成墙深度达到56.7 m,但考虑厚度仅有0.7 m,所以计算模型宽度设为100 m,深86 m。模型底部边界设置竖向约束,左右两边边界设置水平约束,有限元模型和网格划分见图3。

图3 有限元模型Fig.3 Finite element model used in analysis
3.2 土体本构模型和计算参数
在有限元计算中土的本构模型选择非常重要。对于基坑工程,土体的应变一般位于0.01~0.1%小应变范围内。试验表明[6],土体的刚度与应变有着密切的关系,尤其当土体发生小应变时,土体的刚度远大于较大应变阶段的刚度。本文选用可考虑土体小应变特性的HSS模型来模拟土体的应力-应变关系。HSS模型由Benz[7]在HS模型的基础上进一步修正而来,即继承了HS模型可以考虑剪切硬化和压缩硬化的特点又可以考虑剪切刚度在微小应变下随应变衰减的行为。HSS模型参数仅比HS模型参数多了2个考虑小应变行为的参数计算所用参数见表2。表中,c′、φ′ 根据室内三轴固结排水试验确定;的确定可参考王卫东等[8]试验结果,其中刚度参数是通过与室内侧限压缩试验得到的Es0.1-0.2的比例关系确定;分别根据现场波速实验和室内小应变试验得到。
3.3 成墙过程模拟
TRD成墙过程模拟与地下连续墙成槽过程模拟[9]存在一定的区别。地下连续墙成槽是由成槽机械分层开挖,而TRD成墙是由切割箱达到最终开挖深度后进行水平切割,一次性开挖完成。因此对于TRD成墙过程的模拟如图4所示,即一次性开挖到所需深度,并在开挖面左右边界施加线性压力及在开挖面底边界施加均匀压力来模拟流态水泥土浆液的作用,在有限元中成墙过程分析步骤如下:
① 初始条件。墙体开挖前,使土体在K0应力状态下平衡,其中K0=1 - s inφ′。
② 槽壁开挖。杀死所要开挖土体单元直至所需深度,并在开挖左右边界面施加σ=γbentoniteh的线性压力,根据现场施工测试水泥土浆液的重度γbentonite=14.3kN/m3。开挖底面施加压力σ=γbentoniteHe,其中He表示最终开挖深度。

图4 TRD成墙模拟Fig.4 Simulation of TRD trenching wall
3.4 结果分析
图5为距离墙体1.4 m和5 m处的土体侧向位移有限元计算结果和监测数据对比。从图中可以看出,土体侧向位移呈现悬臂开挖的变化趋势,最大侧向位移位于地表,深层土体位移随着深度的增加逐渐减小;深度小于20 m的土体侧向位移明显大于深度大于20 m的土体侧向位移,因为在小于20 m深度内存在较软的第③、④层淤泥质黏土,而大于20 m深度是相对较好的土层的原因。由图5(a)中计算结果和实测值的对比可见,有限元结果和实测数据略微有些差异,尤其在深度20 m以下,计算结果略小于实测值,但变化趋势基本相同。监测数据显示最大侧向位移位于顶口,达到45 mm,而计算结果最大位移仅为17 mm。通过和其他测斜点对比分析,该点监测数据远大于其他深度数据,可能是由于该点位于地表,受到外部施工荷载影响所致;深度3 m处,监测的侧向位移减小至11 mm,在深部20 m后有略微增大趋势,然后在47 m处减小到7.5 mm;而计算结果显示,在小于20 m深度时位移减小较快,超过20 m深度后位移减小较慢。从图5(b)中有限元计算结果和监测数据对比可以看出,计算结果和监测数据基本一致,最大侧移位于地表,大约在14 mm左右。

表2 HSS模型参数Table 2 Parameters for HSS model

图5 距离TRD墙体4 m和5 m处土体侧向位移Fig.5 Soil lateral displacement at 4 m and 5 m from TRD wall
图6为有限元计算的地表沉降结果和实测数据的对比。从图中可以看出,靠近墙体处沉降最大,随着距离的增大,沉降逐渐减小且慢慢趋于稳定;实测值和计算结果对比表明,二者变化趋势基本一致,监测数据显示成墙结束时最大沉降达到12 mm左右,到42 m处地表沉降逐渐减小到4 mm左右;最大沉降约为15 mm左右,最小沉降为5 mm左右。

图6 地表沉降曲线Fig.6 Ground settlement curves
3.5 参数分析
章节3.4将有限元结果与实测值进行了对比,验证了有限元结果的可靠性,为了进一步研究TRD成墙施工对周边环境的影响,本节将建立不同成墙深度的模型来分析成墙引起的土体位移。土体参数与本构模型与前述一样,保持墙体宽度0.7 m不变,墙深分别设为He=20、30、40、50 m。
图7为距离墙体1.42 m处的不同成墙深度的土体侧向位移曲线。从图中可以看出,不同成墙深度的位移变化形态类似,侧向位移均发生在成墙深度范围内,最大侧向位移均发生在地表,深度越深,最大侧向位移越大。56.7 m深成墙最大侧移17 mm;20 m深成墙最大侧移为10 mm。图8为不同城墙深度的地表沉降有限元计算结果。从图中可以看出,不同成墙深度下的沉降曲线变化趋势一致,随着距离墙体距离越远,沉降值逐渐减小,直到稳定值。成墙深度越深,沉降值越大,稳定后的值也越大,如成墙深度20 m的最大沉降为8.5 mm,稳定后最小值1.0 mm左右,成墙深度为50 m的最大沉降为12 mm,最小沉降为5 mm左右。

图7 不同成墙深度对土体侧向位移的影响Fig.7 Influence of wall depth on lateral soil displacement

图8 成墙深度对地表沉降的影响Fig.8 Influence of wall depth on ground settlement
图9为TRD不同成墙深度的归一化地表沉降曲线与 Clough等[10]根据多个基坑工程案例统计的地下连续墙成槽沉降包络线对比图。从图中可以看出,TRD成墙引起的地表沉降位于地下连续墙成槽包络线范围内,图中虚线可以视为 TRD成墙沉降包络线,其最大地表沉降约为 0.05%H,沉降影响区域大概在1.8倍成墙深度左右。

图9 不同成墙深度的地表沉降曲线Fig.9 Ground settlement curves of different wall depths
4 结 语
采用有限元方法并基于土体小应变本构模型模拟了 TRD工法成墙试验引起的土体侧向位移和地表沉降,得到了与实测较一致的结果,为分析TRD成墙对环境的影响提供了分析方法。进一步研究了不同成墙深度情况下的土体变形情况,结果表明成墙深度越大,土体侧向变形和地表沉降也越大;土体侧向变形呈现出类似悬臂梁的变形性态;TRD成墙引起的最大地表沉降约为 0.05%H,沉降影响区域约为1.8H,TRD成墙引起的地表沉降较Clough等[10]统计的地下连续墙成槽引起的地表沉降要小得多。
[1] SCHAFER R, TRIANTAFYLLIDIS T. The influence of the construction process on the deformation behaviour of diaphragm walls in soft clayey ground[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(7): 563-576
[2] 王卫东, 常林越, 谭轲. 采用 TRD 工法控制承压水的邻近地铁深基坑工程设计与实践[J]. 岩土力学, 2012,42(5): 168-171.WANG Wei-dong, CHANG Lin-yue, TAN Ke. Design and practice of a deep excavation using TRD construction method cutting off confined water nearby subway tunnel[J]. Rock and Soil Mechanics, 2012, 42(5): 168-171.
[3] 李星, 谢兆良, 李进军, 等. TRD工法及其在深基坑工程中的应用[J]. 地下空间与工程学报, 2011, 7(5): 945-950.LI Xing, XIE Zhao-liang, LI Jin-jun, et al. TRD method and its applications in the deep excavation engineering[J].Chinese Journal of Underground Space and Engineering, 2011, 7(5): 945-950.
[4] 王卫东, 邸国恩. TRD工法等厚度水泥土搅拌墙技术与工程实践[J]. 岩土工程学报, 2012, 34(增刊1): 628-633.WANG Wei-dong, DI Guo-en. Engineering practices of constant thickness steel cement-soil wall constructed by TRD method[J]. Chinese Jounal of Geotechnical Engineering, 2012, 34(Supp.1): 628-633.
[5] 王卫东, 翁其平, 陈永才. 56 m深TRD工法搅拌墙在深厚承压含水层中的成墙试验研究[J]. 岩土力学, 2014,35(11): 3247-3252.WANG Wei-dong, WENG Qi-ping, CHEN Yong-cai.Experimental investigation of construction of a 56 m thickness cement-soil wall using trench cutting re-mixing deep deep constant wall (TRD) method in deep aquifers[J]. Rock and Soil Mechanics, 2014, 35(11):3247-3252.
[6] ATKINSON J H. Non-linear soil stiffness in routine design[J]. Géotechnique, 2000, 50(5): 487-508.
[7] BENZ T. Small strain stiffness of soils and its numerical consequences[D]. Stullgnt: University of Stuttgart, 2006.
[8] 王卫东, 王浩然, 徐中华. 上海地区基坑开挖数值分析中土体HS-Small模型参数的研究 [J]. 岩土力学, 2013,34(6): 1767-1774.WANG Wei-dong, WANG Hao-rang, XU Zhong-hua.Study of parameters of HS-Small model used in numerical analysis of excavations in Shanghai area[J].Rock and Soil Mechanics, 2013, 34(6): 1767-1774.
[9] GOURVENEC S M, POWRIE W. Three-dimensional finite-element analysis of diaphragm wall installation[J].Géotechnique, 1999, 49(6): 801-823.
[10] CLOUGH G W, O’Rourke T D. Construction induced movements of in situ walls[C]//Proceedings of Conference on Design and Performance of Earth Retaining Structures. New York: Geotechnical Special Publication, 1990: 439-447.
