基于DOB和ZPETC的PWM驱动快速反射镜控制方法研究*

王福超，田大鹏 ，王昱棠

(中国科学院航空光学成像与测量重点实验室中国科学院长春光学精密机械与物理研究所，吉林长春130033)

0 引 言

随着航空成像设备的不断发展，成像设备的探测距离已由十几公里逐步提升至几十公里、甚至几百公里，随着探测距离的不断提升，对成像设备的稳定精度要求也越来越高。目前国内稳定平台所能达到的稳定精度在25 μrad(RMS)，国外稳定精度可以达到5 μrad(RMS)。针对载体扰动的抑制问题，传统方法通过两轴两框架或两轴四框架结构隔离载体扰动，由于机械结构特性以及电机力矩限制，系统的带宽及稳定精度难以在本质上得到进一步提升。因此，通过引入复合轴系统实现高精度视轴稳定［1-2］。复合轴结构是在大惯量跟踪架的主光路中装方位、俯仰均可微动的高谐振频率快速反射镜(fast steering mirror，FSM)［3］。快速反射镜具有体积小、质量轻、结构紧凑、速度快、精度高、带宽高等优点［4-5］，广泛应用于空间光通信、像移补偿以及高精度跟踪瞄准等领域［6-7］。快速反射镜通常采用压电陶瓷和音圈电机(voice coil motor，VCM)进行驱动［8］。压电陶瓷驱动方式可以提供较大的力矩输出，以及高带宽响应，但该种驱动方式反射镜的角位移行程较小，并且驱动电路复杂、功耗高。基于音圈电机快速反射镜角位移行程较大，可以达到10°～15°范围，并且动态特性好。音圈电机通常采用PWM 和线性放大器两种方式进行驱动。线性放大器驱动方式驱动器线性度较好，但驱动效率低、发热量大。PWM 驱动方式可以提高驱动器的效率，并且功耗较低。

传统的直流力矩电机通过引入电流闭环控制，可以改变速度回路控制对象的特性，提高控制系统的跟踪精度［9-10］，并且可以简化系统的数学模型。但由于音圈电机反射镜自身惯量较小，电机输出力矩较大，采用电流闭环方式进行驱动，音圈电机极易受到外界噪声以及控制电流噪声的影响，影响反射镜的控制精度。采用PWM 电流开环驱动方式可以消除电流噪声的影响，但摩擦力矩、不平衡力矩以及模型摄动等因素都将影响控制器的实际实现效果［11-12］，反射镜通常不能满足高精度、高带宽、高刚度的要求。

为了获得更好的动态性能和刚度，本研究提出一种基于ZPETC 及DOB 的音圈电机快速反射镜控制器。笔者研究内容安排如下:

(1)辨识高精度系统模型。根据系统动力学特性，建立系统模型的数学表达式。通过实验给出PWM驱动方式的特性。

(2)控制算法设计。针对PWM 驱动方式所存在的问题，以及快速反射镜存在的扰动、模型摄动问题，建立基于干扰观测器的扰动抑制控制器，并且设计零相差前馈控制器，进一步提高系统的跟踪性能。

(3)实验验证以及实验结果分析。通过扫频方式拟合出系统精确的数学模型，建立基于ZPETC 和DOB的复合控制方法，并通过实验平台进行验证，分析实验结果。

1 系统模型

音圈电机是直线电机的一种，其体积较小、具有良好的动态响应特性、并且控制方便，因此特别适合高带宽、高精度的运动控制。音圈电机物理模型如图1所示。

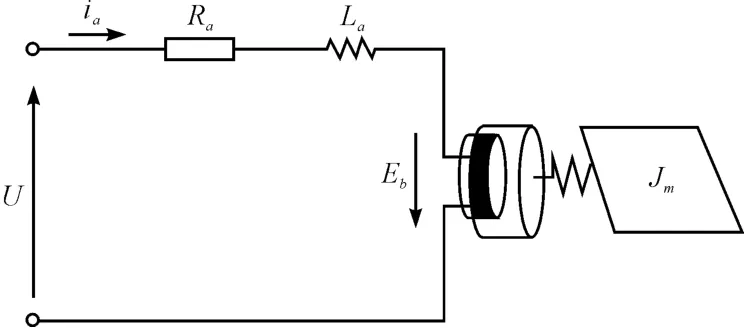
图1 音圈电机物理原理图

在实际机械伺服系统中，机械谐振模态普遍存在，其产生原因是传动轴并非完全刚性，受力后发生弹性扭曲变形。对于音圈电机直接驱动伺服系统，考虑机械谐振模态的情况下，一般采用双质量体模型来描述系统动态。根据快速反射镜动力学特性建立系统方框图如图2 所示。

图2 考虑谐振模态的快速反射镜系统框图

本研究采用PWM 电流开环方式驱动快速反射镜运动。在电流开环的情况下利用伪随机噪声作为模型辨识的输入信号，通过Matlab 模型辨识工具箱对被控对象传递函数进行辨识，输入信号与输出信号如图3所示。辨识得到的快速反射镜电流开环系统模型如图4 所示。

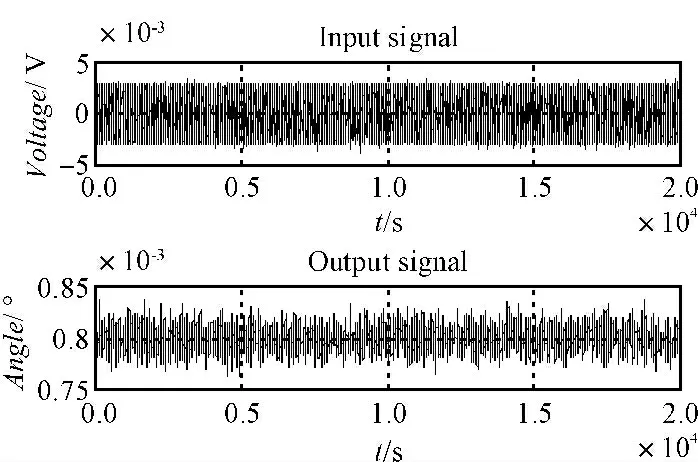
图3 电流开环系统辨识输入信号与输出信号

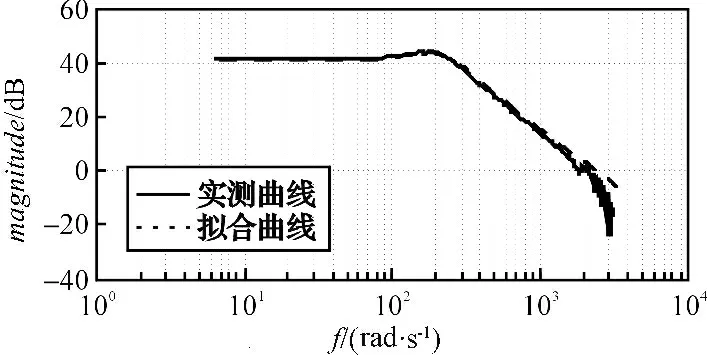
图4 快速反射镜电流开环系统模型

拟合得到系统传递函数:

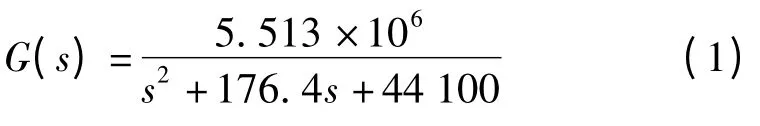
从图4 的拟合结果可以看出系统在200 rad/s 的频率点出现谐振峰值，因此需要加入阻尼系数消除该谐振点的影响。根据式(1)可知系统为二阶系统:

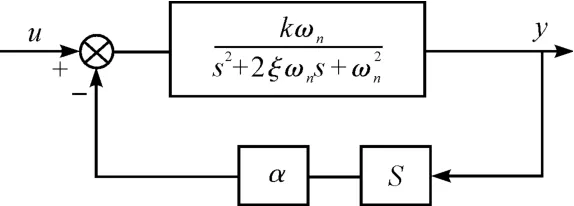
图5 加入阻尼系数环节

根据图5 所示的框图可知，改变α 的值可以改变系统的阻尼系数，消除系统的谐振点影响。通过计算取α=0．000 03 拟合加入阻尼之后系统模型:

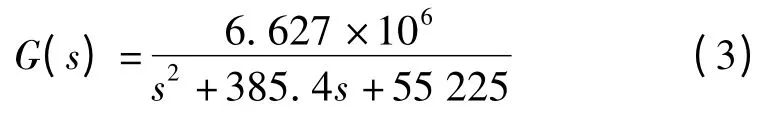
图6 加入阻尼后拟合结果

2 快速反射镜鲁棒控制系统

由于采用电流闭环的方式进行驱动使得驱动电流的噪声较大，影响音圈电机的控制精度，本研究针对该问题采用电流开环的方式进行控制，并且采用ZPETC和DOB 的复合控制方法提高反射镜的控制精度以及系统带宽。

Tomizuka M［13］在完全跟踪控制思想的基础上提出了零相位跟踪控制器［14］，ZPETC 方法可以提高系统的跟踪性能，有效地解决系统延时问题，但由于是开环控制，控制器的性能依赖被控对象数学模型的精确性。首先应对被控系统进行闭环控制，在一定程度上减小外界干扰以及被控对象模型参数变化对ZPETC 控制性能的影响。干扰观测器［15］是一种根据内模原理设计的控制方法，其能够检测出系统的干扰力和模型波动，并且克服机械非线性、摩擦以及模型参数变化对控制器性能的影响，并且能够使系统模型保持鲁棒性。为此，本研究设计了基于干扰观测器的鲁棒控制方法，克服了系统参数变化对系统性能的影响。在低频段使得实际被控对象的响应逼近名义模型的响应，在此基础上笔者采用ZPETC 进行补偿，使系统相位为零，幅值近似为1。

2．1 干扰观测器原理

干扰观测器的基本原理是测量外部力矩干扰及模型参数变化造成的实际对象与名义模型输出的差异，并将此估计值作用于系统达到消除干扰的目的。DOB的基本原理图如图7 所示。

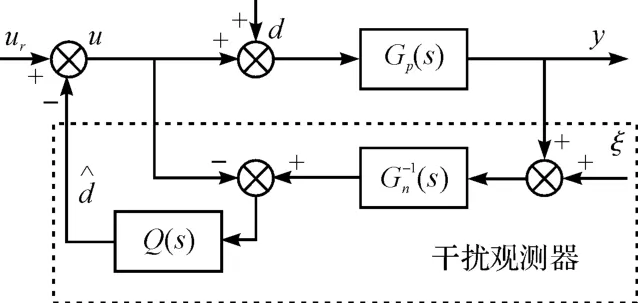
图7 干扰观测器原理框图

系统的输出y 为:

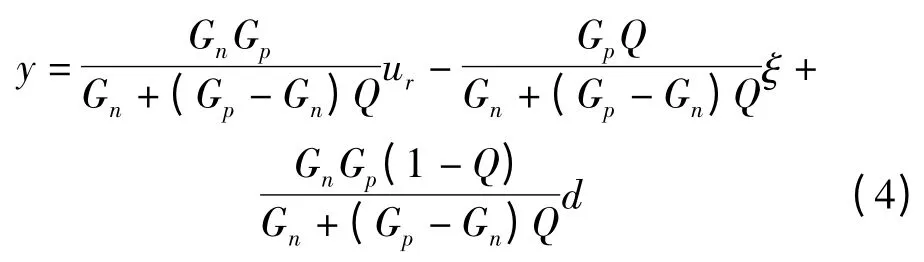
当系统被控对象和系统的标称模型相同的时候系统的输出y 为:

其中:Q(s)—具有低通滤波特性，在低频段Q(s)=1，在高频段可以认为Q(s)=0。由式(5)可以看出在低频段即使系统存在干扰，系统也可保证较好的鲁棒性。

经过分析可知，带有干扰观测器的系统灵敏度函数和补灵敏度函数为:

系统鲁棒稳定的充分必要条件是:

其中:ΔM=Gp(s)-Gn(s)。

由上式可以看出滤波器的设计结果直接影响干扰观测器的稳定性。

通常滤波器的设计结构如下:

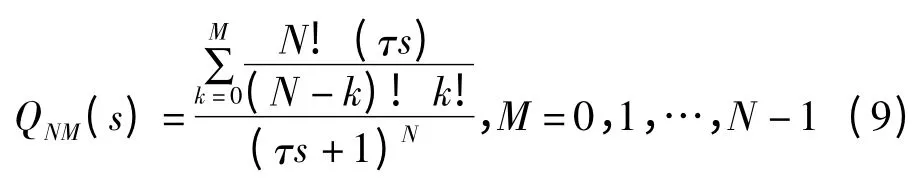
式中:N—分母阶数，M—分子阶数。

在进行滤波器Q(s)设计过程中对分子分母的阶数给予如下考虑:

(1)对于谐振频率较高的系统，可与选择较大的分子阶数来保证系统的抗干扰能力以及减小系统干扰估计的相位滞后。

(2)若系统的谐振频率较低，可以选择Q(s)的分子阶数为0，再调整截止频率和分母阶数，在抗干扰能力和稳定性之间折衷。

(3)设计Q(s)的分母时，应使Q(s)的相对阶不小于被控对象名义模型Gn(s)的相对阶，以保证Q(s)正则，物理可实现。

2．2 零相差前馈控制控制器

为了提高系统的动态跟踪性能，Tomizuka 提出了ZPETC，其基本思想是基于零极点对消。其基本结构如图8 所示。

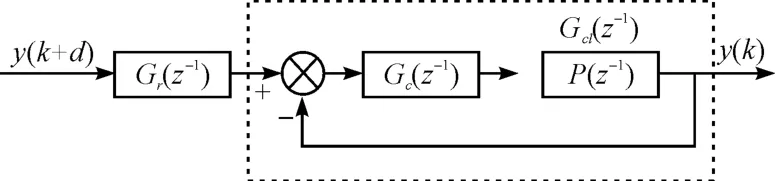
图8 ZPETC 结构框图

加入控制器的闭环系统经过双线性变换可以得到如下形式的离散传递函数:

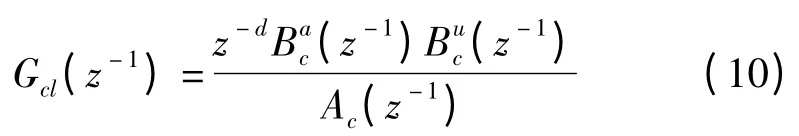
式中:z-d—系统d 步延时，—闭环传递函数分子多项式中包含稳定零点的部分，—分子多项式中包含不稳定零点的部分。

考虑上述离散闭环传递函数，设计ZPETC 控制器:

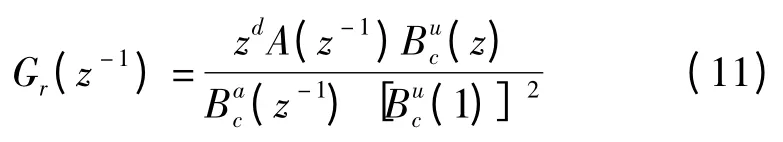
则整个系统的传递函数为:

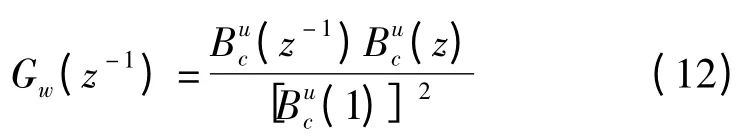
当z=ejωt时，系统的传递函数为:

从式可以看出传递函数是一个不含虚部的非负实数，因此在系统的相移在整个频域内为0，在一定范围内幅值接近为1。

3 实 验

本研究以音圈电机快速反射镜为对象进行了实验验证，音圈电机如图9 所示。实验平台原理框图如图10 所示。控制系统以HRT1000 半实物仿真系统为核心，控制算法通过Matlab Simulink 进行搭建，并在Vx-Works 实时操作系统上运行。控制信号通过PCI 总线上的16 位D/A 转换卡与电机驱动器相连，反馈信号通过A/D 转换器进行采集，系统的采样时间为1 ms。

图9 音圈电机驱动快速反射镜

图10 实验平台原理框图

首先，本研究针对式(3)进行DOB 和PID 控制器设计。引入DOB 和PID 后的扫频结果如图11 所示。考虑式被控对象的名义模型，根据3．1 节的论述设计滤波器Q(s)，本研究采用二阶滤波器形式，并且取τ=0．000 8:

PID 控制器取kp=0．2，ki=15，kd=0。针对引入DOB 和PID 控制器的闭环系统，通过正弦扫频的方式拟合获得系统闭环频率特性及传递函数:

接着设计ZPETC。针对上述传递函数设计ZPETC控制器:

图11 引入DOB 和PID 后的扫频结果

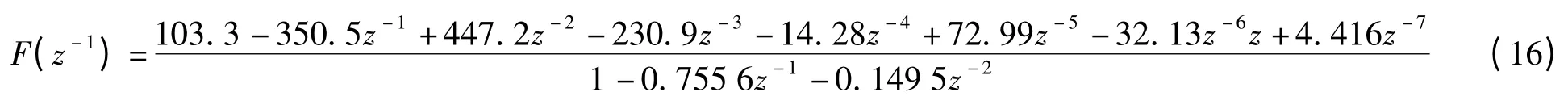
针对上述设计的控制器，在反射镜0 输入条件下系统的静态误差如图12 所示。从图12 中可以看出反射镜的静态误差为26．2 μrad。采用PWM 电流闭环方式的静态控制精度如图13 所示。比较图12 和图13结果可以看出，引入ZPETC 和DOB 后的静态控制精度明显高于电流闭环驱动方式。

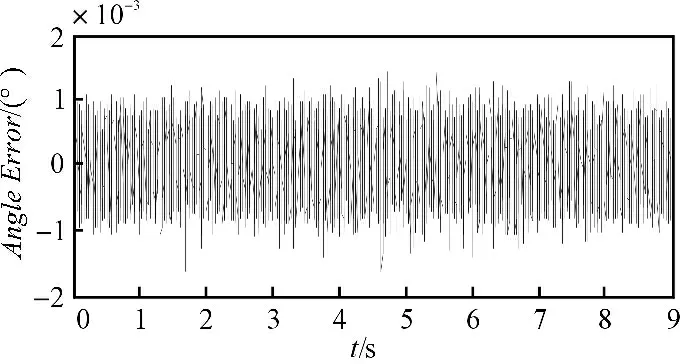
图12 基于ZPETC 和DOB 控制的静态控制精度

图13 采用PWM 电流闭环静态控制精度

加入ZPETC 的闭环系统频率特性如图14 所示。从实验结果可以看出加入ZPETC 后反射镜的控制带宽可达到150 Hz，采用ZPETC +PID +DOB 的控制策略保证了反射镜电流开环的情况下有较高的定位、跟踪精度，并且有效地抑制了外界干扰对控制器性能的影响。

4 结束语

本研究针对音圈电机快速反射镜的PWM 驱动方式设计基于DOB 和ZPETC 的控制方法，通过DOB 克服了摩擦力矩、不平衡力矩以及模型不确定性的因素的干扰，提高系统的鲁棒性;同时通过设计ZPETC，保证了系统的快速性和跟踪精度。实验结果表明，笔者设计的控制算法能够很好地保证反射镜的跟踪性能，同时零相差前馈控制方法保证系统控制带宽达到150 Hz，有效改善系统动态性能。

图14 引入零相差之后系统的闭环频率特性

［1］杨 东，毛 耀，丁 科，等．模型参考算法在快熟反射镜中的应用［J］．红外与激光工程，2013，42(10):2790-2795．

［2］徐飞飞，纪 明，解 静，等．FSM 在高精度瞄准线稳定系统中的应用研究［J］．应用光学，2012，33(1):9-13．

［3］彭树萍，于洪君，王伟国，等．新型快速反射镜伺服系统设计［J］．红外与激光工程，2014，43(5):1610-1615．

［4］KLUK D ，BOULTE M T，TRUMPER D L． A high-bandwidth，high-precision，two-axis steering mirror with moving iron actuator［J］．Mechatronics，2012(22):257-270．

［5］黑 沫，鲁亚飞，张智永，等．基于动力学模型的快速反射镜设计［J］．光学精密工程，2013，21(1):53-61．

［6］鲁亚飞．快速反射镜机械结构特性设计问题研究［D］．长沙:国防科技大学机电工程与自动化学院，2009．

［7］NÉSTOR O，ARANCIBIA P，GIBSON，et al． Frequencyweighted minimum-variance adaptive control of laser beam jitter［J］． IEEE/ASME Trans． Mechatronics，2009，14(3):337-348．

［8］YU Hsing-cheng，CHEN Tsan-chen，LIU Chien-sheng． Adaptive fuzzy logic proportional-integral-derivative control for a miniature autofocus voice coil motor actuator with retaining force［J］．IEEE Trans． Magn，2014，50(11):243-250．

［9］黄永梅，张 桐，马佳光，等．高精度跟踪控制系统中电流环控制技术研究［J］．光电工程，2005(32):16-19．

［10］丁 涛．一种光电转塔精确跟踪算法［J］．兵工自动化，2013(4):82-84．

［11］LIU C-S，KO S-S，LIN P-D． Experimental characterization of high-performance miniature auto-focusing VCM actuator［J］．IEEE Trans． Magn．，2011，47(4):738-745．

［12］TANG Tao，MA Jia-guang，REN Ge． PID-I controller of charge coupled device-based tracking loop for fast-steering mirror［J］．Optical Engineering，2011，50(4):643-655．

［13］TOMIZUKA M． Zero phase error tracking algorithm for digital-control［J］． Journal of Dynamic Systems Measurement and Control-Transactions of the Asme，1987，109(1):65-68．

［14］李志军，刘成颖，孟凡伟，等． 基于ZPETC 和DOB 的直线电机控制器设计及实验研究［J］．中国电机工程学报，2012，(24):134-140．

［15］OHNISHI K，SHIBATA M，MURAKAMI T． Motion control for advanced mechatronics［J］． IEEE/ASME Transactions on Mechatronics，1996，1(1):56-67．